BP和SAE深度神经网络方法的织物缺陷检测研究

严 伟，杨 朔

（1.浙江省科技信息研究院，浙江 杭州 310006；2.浙江天正信息科技有限公司，浙江 杭州 310006）

0 引言

我国作为世界上丝绸织物的最主要产地，丝绸从古代开始，就成为了我国与外国贸易的重要组成部分。也因为丝绸织物的贸易，从而产生了“陆上丝绸之路”和“海上丝绸之路”。到了近现代，我国的丝绸制造业在世界范围内也仍处于领先地位。但是在织物花纹缺陷检测的过程中，传统的人工检测花费时间长、人力成本高等缺陷也暴露出来，影响了我国各类织物产品的市场竞争力。在实际生产中，最小的织物缺陷大小仅为0.5毫米[1]，一个熟练的操作工平均每分钟能够检测长度为17米、宽度为1米左右的织物。如果工人长时间工作，则会导致效率下降，甚至会遗漏重要的缺陷和疵点。如果改用摄像头获取图像，再通过计算机使用深度神经网络的算法来检测采集到的织物缺陷类型，则既可以缩短检测时间，也可以减少人力成本，提高经济效益。

1 BP神经网络

如图1所示是最简单的神经元，x为输入量，+1是偏移，h为输出量。

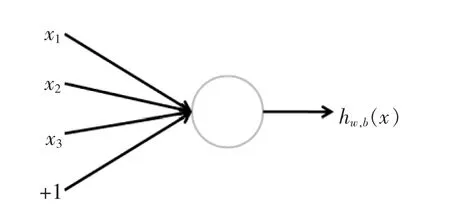
图1 最简单的神经元

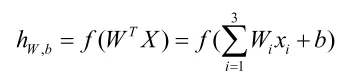
f（x）是激活函数，它有两种形式，一种是sigmoid形式，另一种是tanh形式。公式分别为：

sigmoid函数值范围为[0，1]，而 tanh函数值范围为[-1，1]。

BP神经网络[2]可以学习大量的输入和输出关系，且效果非常好。它是一种多层前馈神经网络（Feedforward Neural Network），由3层组成：输入层、隐藏层和输出层。前一层与后一层相互连接，但是本层的信号元之间并不相连，隐藏层的数量可以是一层或者一层以上，BP神经网络模型如图2所示。

图2 BP神经网络模型

神经元的层与层之间交流由两种组成：第一种是工作信号，是一种在输入层输入然后在输出层输出的向前传播的信号；第二种是误差信号，它是实际输出与期望输出的误差，从输出端开始逐渐向前（即输入端方向）传播。BP神经网络是前向传输和误差反向传播相结合的一种网络。开始时，通过在输入层输入，再一层一层的向后传播，直到输出层。此时通过比较输出层的实际输出和期望输出，如果相差很大，则会进入误差反向传播过程[2]，误差信号按原路返回，调节阈值和权值，然后重复计算。由于BP神经网络简单、效果好的特点，所以被广泛使用，但同时也有很多缺点，比如需要反向传播，所以它学习效率低，收敛速度相对较慢。

针对BP神经网络的缺点，提出了3种解决方法：

（1）附加动量

附加动量是在网络在反向传播修正权值的时候，考虑误差在梯度上的作用和误差曲面的变化趋势。

（2）自适应学习速率

一般情况下，学习速率通常由经验或者实验得到，但是此数据未必有好的效果，故需要神经网络自动调节学习速率。如果实际误差过大，可以调高学习速率；如果出现过调的情况，就需要降低学习速率。

（3）动量—自适应学习速率

动量附加的方法，可以获得最优解；自适应学习速率法，则可以减少学习时间。故将两者结合可以得到一个效率高、训练时间短的神经网络。

2 SAE神经网络

2.1 自动编码器（AE）

AE[3]是指AutoEncoder自编码模型，是一种无监督学习算法，分为输入层、隐藏层和输出层3层，其中输入层和输出层的维数相同。

自动编码器是一种尽可能展现原始输入信号的神经网络，它先把输入：

映射到：

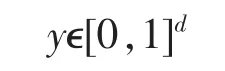
其公式是

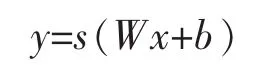
s为非线性函数，这个过程是编码过程。与其相对应，把y转化为z则称为解码过程。

整个过程被称为重构过程。重构过程中的损失函数为：

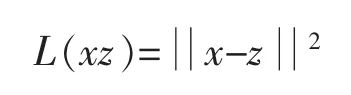
在开始时输入一个输入量，此输入量经过一个编码器Encoder，得到Code，然后再经过一个解码器Decoder，得到输出。把输出和输入比较，如果两者非常相近，则Code就可以作为一个特征向量。然后不断调整Encoder和Decoder，使输出和输入的误差最小，如图3。

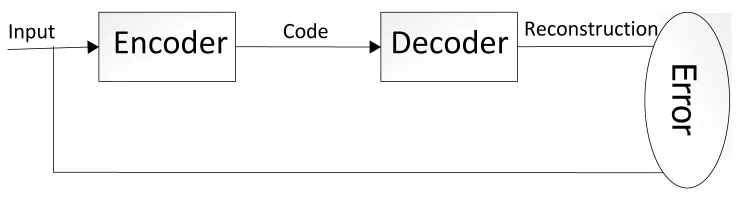
图3 AE工作原理

2.2 去噪自编码器（DAE）

DAE[2]是去噪自动编码器，其结构和AE几乎一致，只是在样本中加入了一些具有噪声的训练样本，这样可以训练从受污染的样本中提取纯净的输入。去噪自动编码器认为在AE的过程中，提取到的特征不一定是完善的，应该在其中添加噪声，这样才可以提高特征向量的鲁棒性和纯洁性。

在原训练样本X中加入噪声得到样本，经过重新编码后得到Y，再把Y解码重新得到重构向量Z，损失函数即为 LH（X，Z）。 DAE与 AE 的主要区别在于加入了噪声，得到更纯净性的特征向量，具体的去噪自动编码器的流程如图4所示。

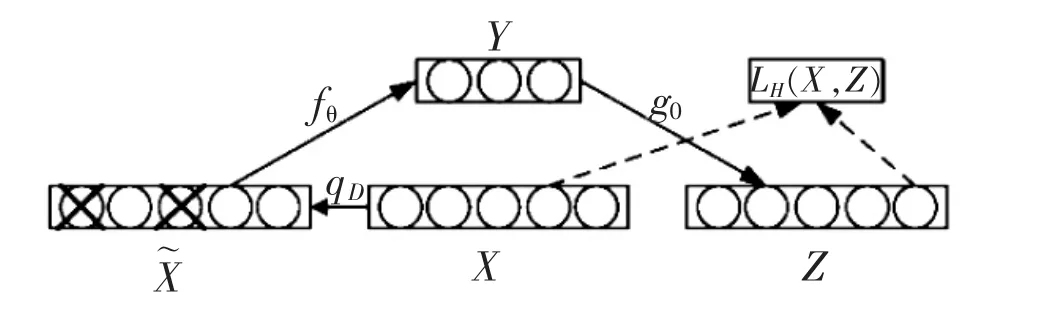
图4 去噪自动编码器的原理图

2.3 稀疏自动编码器（SAE）

稀疏自动编码器[3]也是编码器的一种，同样要求输出和输入的维度相等，并且它的隐藏层必须是稀疏的，也就是说隐藏层是经过压缩的，那么就会导致丢失一定的信息。稀疏编码的公式为：

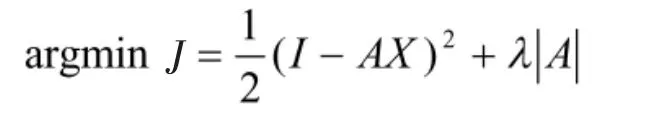
假设输入层的维度为m*n，那么根据自动编码器的原理可得输出层的维度也为m*n，把隐藏层的维度设置为 x*y（x*y＜m*n），那么这样就可以得到稀疏编码，它的实质就是降维。如图5所示，Layer L1是输入层，编码后得到隐藏层Layer L2，L2的维度小于L1，进行压缩后再次解码，得到和L1维度相同的输出层Layer L3，这就是稀疏编码器。L1中的节点大部分为0，小部分为1；如果使用tanh作为激活函数，则大部分节点为-1。

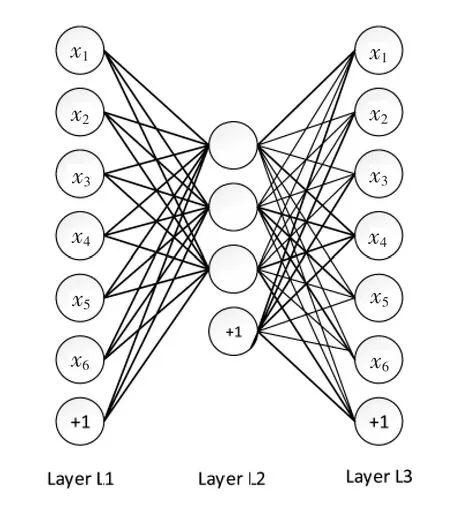
图5 稀疏自动编码器的原理

3 基于BP神经网络的织物缺陷检测

3.1 织物缺陷的种类介绍

实际生产中较为常见的疵点：

破洞：织物的线横向和纵向断裂均超过3根；

污渍：织物由于其他原因导致花纹产生瑕疵；

杂物：在生产中，由于木屑或者其他东西卡入织物中而产生的瑕疵；

经疵：纵向的图案花纹缺陷；

纬疵：横向的图案花纹缺陷。

这些缺陷在实际生产中仅仅占一小部分，还有其他种类的缺陷，比如：横档、棉球、双经、云织等，这是由不同的缺陷分类标准决定的。

由于受到样本数量和种类较少等因素的限制，本实验主要以正常样本、经疵样本和纬疵样本为例，对样本和标签训练，进行结果的测试。

3.2 BP神经网络的设计

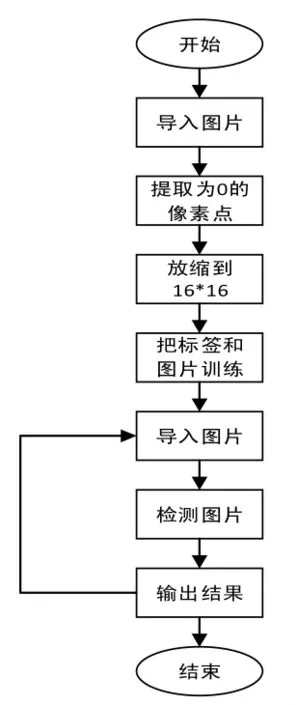
图6 基于BP算法的缺陷检测

网络的层数一般为3层及以上，包括1层输入层、1层输出层和1层或者多层隐藏层[3]。增加网络层数可以提高网络的精度，但是会让网络更加复杂，导致网络的训练时间增加。但是增加隐藏层单元数目比增加隐藏层层数要简单得多，在具体设计中，一般需要多次实验，才能获取最合适的网络以及初始权值。初始权值会直接影响到训练的时间，学习速率过大，则会导致系统的不稳定，过小则会导致训练时间过长。

首先需要对训练样本进行预处理和特征提取，主要是利用图像分割技术消除图像的大小、颜色差异，最后通过归一化操作得到16×16的像素点阵图。由于BP神经网路是一种有监督的学习，都由一个输入对象和一个期望输出组成，所以可以直接输出分类后的结果。把图像和标签一起导入训练，就可以得到所需要的训练集。本实验采用2层的BP神经网络，隐藏层节点数为25，输出层节点数为1。流程如图6所示，在训练结束后，对待测试的图像重新进行测试，表1和表2所示分别为基于BP处理64×64和16×16缺陷图像的正确率与平均时间。

表1 基于BP处理64×64的缺陷图像正确率与平均时间

表2 基于BP处理16×16的缺陷图像正确率与平均时间

由于待测样本存在缺陷过小，花纹复杂等因素，所以会出现缺陷的漏测或误测发生。如图7所示均是直接使用BP神经网络无法检测出的图片，因为缺陷的宽度和长度均不明显，所以程序无法识别出它的缺陷。

图7 较难检测的图像

4 基于SAE神经网络的织物缺陷检测

在程序开始时，先对样本图进行训练，利用SAE深度神经网络进行训练，其中包含4个隐藏层。由于原图大小是64×64，所以输入层为4096维；4 个隐藏层，分别为 1500，500，200，50，编码和解码的过程如图8所示。在这些训练的样本中，还随机加入了部分具有缺陷的样本，使训练出的特征更具有鲁棒性，训练后得到一张64×64图像，称为重构图像，如图9所示。

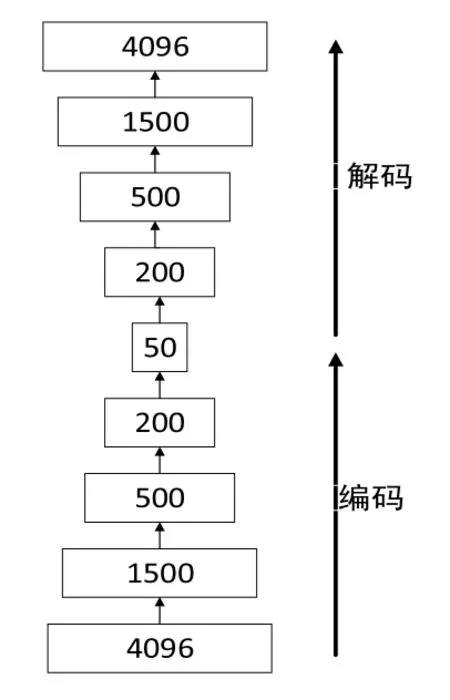
图8 样本的编码和解码过程

图9 训练后的64×64重构图

由于SAE是无监督学习方式，所以它仅能把训练样本的数据集进行重新建模，在测试过程中并不能直接得到该缺陷的具体种类，因此还需要进一步地对测试图像进行手动分类处理。把测试图像和获得的重构图像均作二值化处理后作差，得到的图样即为缺陷图像，如图10所示，从左到右分别为导入图像、重构图像、缺陷图像。但由于织物花纹颜色的多变性，左侧部分的白色小点不是缺陷，而是需要被过滤的噪声，最后得到的缺陷图像如图11所示。在经过多次试验后，得出二值时期的最佳阈值，以及根据缺陷图长宽比值判断为经疵还是纬疵，长宽比值一般设置为0.9和1.1。

图10 缺陷检测结果图

图11 经过滤波后的缺陷检测图

通过对缺陷的判断，最后可以获得织物的检测结果，分为3类：正常、经疵和纬疵。算法的流程如图12所示。第一步是通过大量样本进行训练，500张64×64的样本训练时间为10分钟。然后得到一个训练集以及重构图像。把带检测图像导入作差过滤后的图像就是最终得到的缺陷图像。

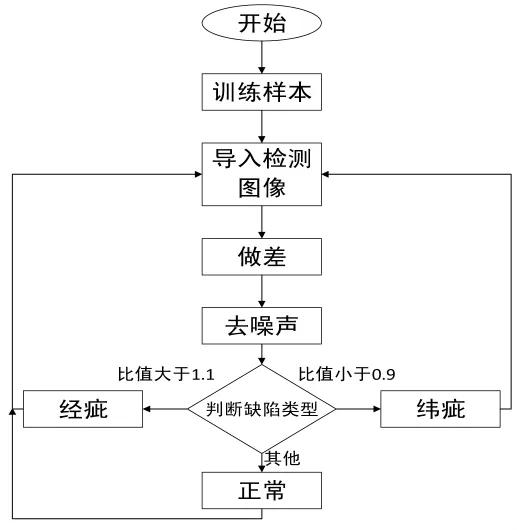
图12 基于SAE算法的缺陷检测流程图

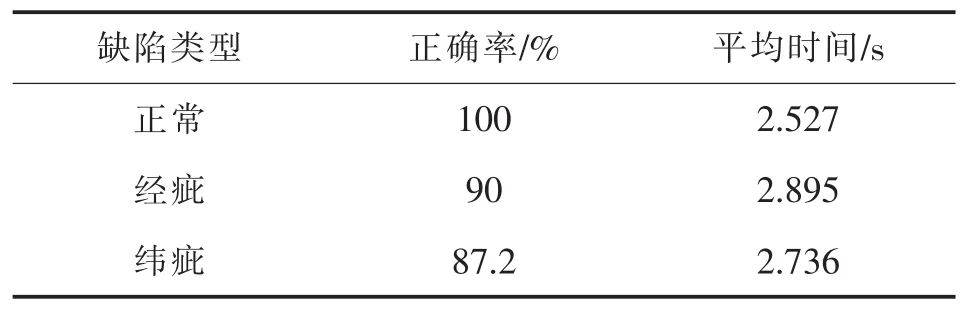
表3 基于SAE处理64×64的缺陷图像正确率与平均时间

表4 基于SAE处理16×16的缺陷图像正确率与平均时间

图13 正常、经疵和纬疵图像

表3和表4是关于SAE处理64×64和16×16大小的图像的数据。从表格中可以看出，正常的图片都可以检测出，经疵绝大部分都可以检测出，但是纬疵也依旧没有得到较高的检出正确率。由图13c）显示，由于部分的纬疵图像缺陷不明显，所以无法检测出原本缺陷，反而会归类到正常的图像中。

5 BP和SAE神经网络对织物缺陷检测的比较

本试验主要进行了4个神经网络测试，分别是SAE检测（64×64大小的图片、16×16大小的图片）、BP 算法检测（64×64 大小的图片、16×16 大小的图片）。本文使用MATLAB 2015a，在CPU为Intel core i5-4288u的计算机上运行程序，以下为4个神经网络的具体运行情况统计。

根据试验结果，不同的算法和不同的图片大小对图片的检测正确率和检测时间都有影响。

（1）由表1和表2对比可以发现，如果同时使用BP算法检测缺陷，在其他条件一致的情况下，如果图像像素越小，则图像检测时间也越短，虽然图像的检测正确率也有所提高，但是效果并不明显。64×64的图像大小约为16×16的16倍，但检测的时间却相差并不多。

（2）比较表3和表4可知，在算法一致的情况下，图像像素越小，图像的正确率越高，图像的检测时间就越短。该情况与（1）基本一致，但是图像检测的时间延长较多。

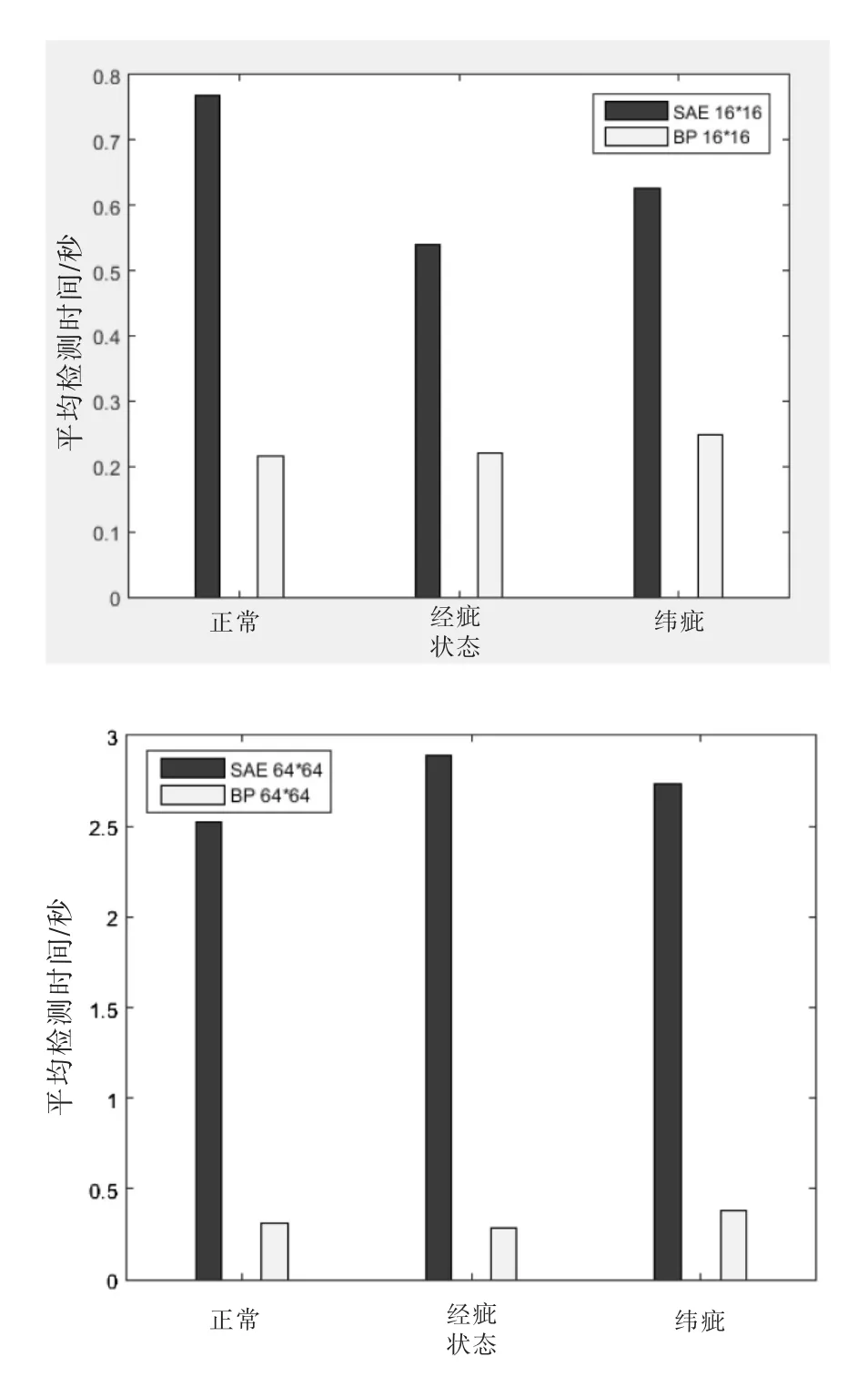
图14 BP和SAE神经网络对织物缺陷检测的平均时间比较

6 结语

缺陷检测算法通常情况下可以分为两大类。第一类是将缺陷区域不同的灰度值变化视为不同的纹理，然后将缺陷识别转化为对图像灰度值以及图像纹理的分析，之后，针对所得到的图像的数据特征，设计一系列的分类规则来对缺陷进行判断。2002年H Zheng针对不平金属表面的缺陷，提出了采用遗传算法学习形态学处理的方法来对缺陷进行检测。2014年Yongxiong Wang等人设计了一种自动管道缺陷检测方法，该方法首先对图像进行分割和特征提取，然后，采用K均值聚类，最后，结合决策树对缺陷做出分析判决。这类算法的优势在于不需要额外的空间来存储模板图像，并能够针对所检测缺陷的特征来设计具体的检测算法。

基于参考的缺陷检测算法是另一类常用的缺陷检测算法。该种方法经常通过模板匹配来获取缺陷。1989年Oli Silven等人利用图像的边缘信息来对印刷电路板进行检测。其具体采用的方法是，首先选择合适的线段作为参考条件，然后对检测图像进行旋转、移动来对模型图像进行对准，在进行缺陷分析时同时采用了统计信息和结构信息。采用该种方法对缺陷进行检测时，在简单的情况下，统计信息能获得较好的缺陷检测结果，但在复杂的情况下，结构信息则更能有利于检测图像中的缺陷。由于该方法在检测相关项目中较为有效，因此很多相关项目中的研究人员都采用类似的方案并对其加以改进。其基本思路均为通过模板匹配，采用待检测图像与模板图像进行差值的方式来进行缺陷检测，这种采用模板进行参考的方式在表面缺陷自动检测中也得到较为广泛地应用。

本文比较了2种基于机器视觉的织物缺陷检测算法，对速度和缺陷检出情况进行了初步的考察。BP神经网络算法作为目前应用最广泛的神经网络模型之一，能够学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。考虑应用的便利性和广泛性，故选择为本次研究对比参考对象。

自动编码器作为无监督深度学习结构，通过编码层对输入数据的非线性编码实现特征提取，在织物缺陷检测中，用于缺陷特征表达的特征向量往往是维数极高，而用于织物检测缺陷训练的样本数却无法达到这一数量级。当特征向量维度超过训练样本数时，容易导致过拟合问题，造成训练误差较小的情况下，实际测试误差偏大。故本文选择SAE算法进行特征提取，通过稀疏化的方式更好地应对此问题。

以机器视觉和深度神经网络的缺陷检测以图像预处理、图像分割算法、图像特征提取为基础，结合一定程度的机器学习，提高算法的准确性、实时性和鲁棒性，是目前缺陷检测高效的关键。在实际生产应用中，检测速度、检测精度（识别率）和对于各种缺陷检测的适应性是非常重要的要素，因此，对这些方面的研究和改进，将会是主要工作。

第一，本文的比较方法基于静态图片，对检测上速度的考察主要针对算法设计；实际应用情况下，更加倾向于在动态环境下采集图像进行在线检测。除去算法，需要设计和考察包含图像采集在内的整个系统。下一步，拟与增加对图像采集部分的研究。

第二，实际生产中，缺陷的情况多种多样，远远超过本测试的范围，并且区分和判断不同的缺陷类型，对生产线的维护和管理也具有积极意义。故针对不同缺陷进行识别和分类的算法研究也是进一步研究的方向。