EXCEL表在超硬复合片计数型抽样检验方案设计中的应用

王智慧，徐文娟，周志成，王文龙，张 喆

(桂林特邦新材料有限公司，广西桂林 541004)

1 引言

超硬复合片具有高硬度、高耐磨性、高导热系数和高加工精度等优点，可实现以车代磨，因之广泛应用于航天航空、汽车及工程机械等高端制造业领域[1]。超硬复合片是高价值的产品，使用商对复合片性能的稳定性提出了很高的要求，希望产品能进行100%检验。然而复合片大多数质量表征指标的检验是破坏性的，只能进行抽检。在设计抽样检验方案时，使用方希望使用方风险质量p1小、使用方风险β低，而生产方则希望生产方风险α低，根据目前的超硬复合片生产水平，生产质量不可能太高，即生产方风险质量p0较大，操作比p1/p0可能会很小，而国标给出的检验方案为[2]：使用方风险β固定为10%，生产方风险α约为5%，操作比p1/p0大于2。若上述要求发生改变，就不能通过查国家标准进行超硬复合片计数型抽样检验方案设计，因此，本文介绍一种利用excel中插入函数进行计数型一次及二次抽样检验方案的设计方法，该方法只需会excel表操作，就会进行计数型一次及二次抽样检验方案设计，可以满足使用方提出的各种特殊质量要求。

2 各概率分布函数的应用范围

利用下节论述的方法设计抽样检验方案时,首先要确定概率分布函数。各概率分布函数的应用范围如表1所示〔3〕。表1中,N为批量,n为样本数,D为批中不合格品数;p为批中不合格品率，p等于D/N，p的取值范围为0～1;p’为批中不合格率(文献〔3〕写成单位产品的缺陷数)，p’取值范围为大于或等于0。为简化起见，本文将不区分p及p’，全用p表示，在计件检验中，p表示不合格品率，在计点检验中，p表示不合格率。

表1 接收概率分布函数

3 计数型抽样检验方案设计简述

计数型抽样分为计件型抽样及计点型抽样[4]。计件型抽样检验是统计样本中的不合格品数，样本中不合格品数必定少于样本数；计点型抽样检验是统计样本中的不合格数，样本中的不合格数可以大于样本数。

GB/T2828标准中将计数型抽样检验分为一次抽样检验、二次抽样检验及五次抽样检验[5]。表2为三种抽样方案优劣对比。

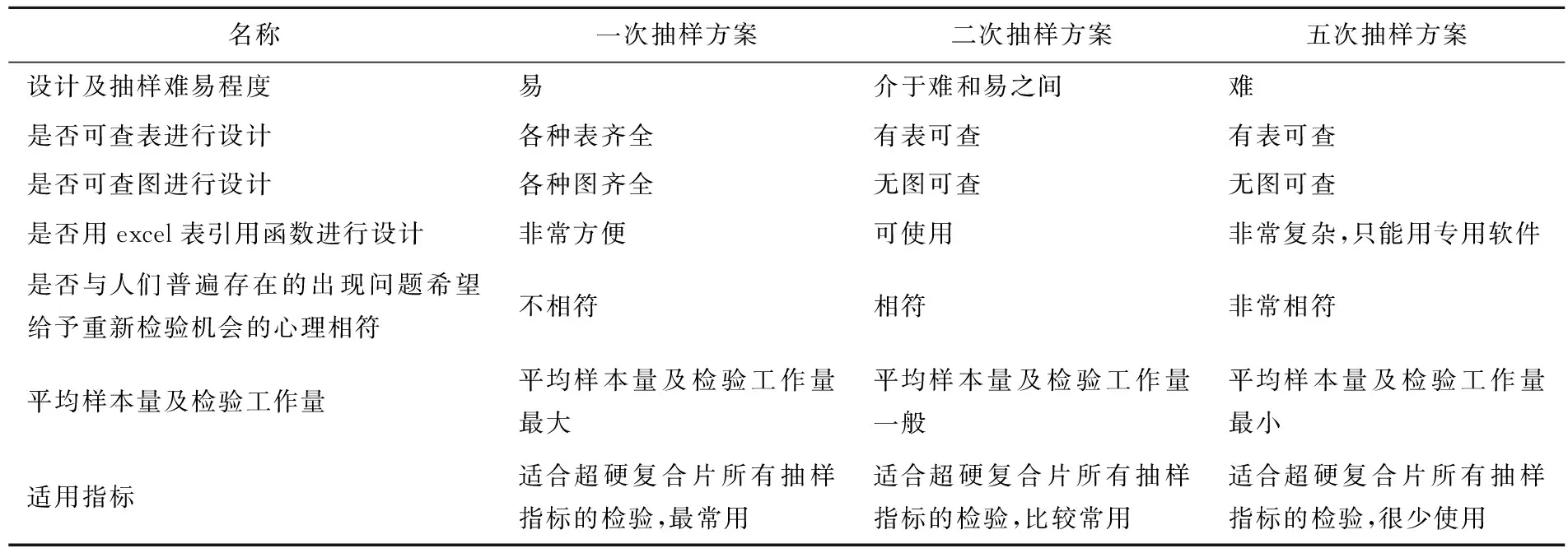
表2 三种抽样方案优劣对比列表

抽样方案设计实际上是在己知使用方风险质量p1、使用方风险β、生产方风险质量p0、生产方风险α的条件下，求抽样检验样本量n、接收数Ac及拒收数Re。

设样本量为n的样本中恰好出现k次不合格品数或不合格数这一事件为X，则X为随机事件，其概率用P{X=k}表示，它是风险质量p、样本量n及不合格品数或不合格数k的函数[6]。

对一次抽样检验方案：设样本量为n1、接收数为Ac及拒收数为Re，则该批产品接收的概率L用下式表示。

根据题意列出下列方程组：

Re=Ac+1;

联合解上列各式,可求得一次抽样检验方案:样本量n1、接收数Ac及拒收数Re。

对二次抽样检验方案：

设第一次抽样检验的接收数及拒收数为AC1和Re1，第二次抽样检验的接收数及拒收数为AC2和Re2,二次抽样检验方案每一次抽样检验的样本量相同，均为n2。

Re2=AC2+1

令：Re1=AC1+m1+1 ；m1=1，2，3……;

m1表示AC1与Re1之间数字的个数，如AC1等于1，Re1等于5，中间有2、3、4共3个数字，则：m1=3;

令：AC2=Re1-1+m2；m2=0、1、2……; 则：AC2=AC1+m1+m2;

令：P0=P{X≤AC1}

P1=P{X=(AC1+1)}*P{X≤[Ac2-(AC1+1)]}=P{X=(AC1+1)}*P{X≤(m1+m2-1)}

P2=P{X=(AC1+2)}*P{X≤[Ac2-(AC1+2)]}=P{X=(AC1+2)}*P{X≤(m1+m2-2)}

……

Pm1=P{X=(AC1+m1)}*P{X≤[Ac2-(AC1+m1)]}=P{X=(AC1+m1)}*P{X≤m2}

L=P0+P1+P2+……+Pm1=F(AC1，Re1；AC2，Re2；n2；p0或p1)

L为接收概率;

根据题意，可列出下列方程组：

L0=F(AC1，Re1;AC2，Re2,n2,p0)=1-α

L1=F(AC1，Re1;AC2，Re2,n2,p1)=β

Re2=AC2+1

要求：AC1，Re1;AC2，Re2,n2全为正整数及尽量小。联合解上述方程可求出AC1，Re1;AC2，Re2及n2。

经查阅资料及参考GB/T 2828系列标准总结出下列规律：

(1)n1/n2≈1.55 ；n1为一次抽样检验方案的样本量，n2为二次抽样检验方案每一次抽样的样本量；

(2)1≤m1≤AC， 0≤m2≤AC;

(3)一般来说：AC≥AC1≥AC/2-2 ；

其中n1、Ac为一次抽样检验方案的样本量和接收数;

五次抽样检验方案设计不适应用excel表的引用函数进行计算。

4 几种常用抽样检验方案设计方法优劣对比

利用上述原理，前人己将计算结果列成表，制成图。因此，抽样检验方案设计常用方法有：查表法、图解法、编程法、excel表计算法，表3列出了它们的优劣及应用范围。

表3 抽样检验方案设计方法优劣及应用范围列表

5 excel表在产品抽样检验方案设计中的应用

(1)excel表插入函数介绍

A.泊松分布

P{X=d}=POISSON(d,λ,FALSE) ；P{X≤d}=POISSON(d,λ,TRUE)

其中λ=n*p为泊松分布的期望值。

B.二项分布

P{X=d}=BINOM.DIST(d,n,p,FALSE) ；P{X≤d}=BINOM.DIST(d,n,p,TRUE)

式中：n为样本量；为d样本中不合格品数或不合格数；p为不合格品率或不合格率。

(2)一次抽样方案设计程序

下面通过举例说明用excel表插入函数进行一次抽样检验方案设计的程序。现对批量N为1000片复合片产品的抗弯强度进行计件型一次抽样检验方案设计,经生产方和使用方协商，得知α为0.0405、p0为0.015、β为0.1、p1为0.1064。其步骤如下：

A.按表1规定确定接收概率分布函数。本例预选用二项分布函数。

B.设计excel表头。表头如图1所示。图1中n10是与生产方同风险α匹配的样本量,n11是与使用方同风险β匹配的样本量，令：B1=n11/n10，B1应尽量接近于1。

C.求样本量n1及接收数Ac。

计算过程及结果如图1所示。

由图1可得出下列结论：

A.当Ac取2，n1、n10、n11取49或50时与要求最接近，当n1为49时对生产方有利，当n1为50时对使用方有利。抽样检验方案以谁优先，最好在合同中约定。若合同中无约定，样本量n1可取中位值。

本例不合格品出现的概率用服从二项分布求解，得Ac等于2，n1等于50或49;由于接收数Ac只能取整数，该解与要求有一定的差距。

当Ac等于2，n1等于50时，若保持风险质量p0等于0.015及p1等于0.1064不变，则生产方风险α为0.0392，使用方风险β为0.0877;若保持生产方风险α等于0.0405及使用方风险β等于0.1不变，则生产方风险质量p0为0.0152，使用方风险质量p1为0.103。当Ac等于2，n1等于49时，若保持风险质量p0等于0.015及p1等于0.1064不变，则生产方风险α为0.0373，使用方风险β为0.0949;若保持生产方风险α等于0.0405及使用方风险β等于0.1不变，则生产方风险质量p0为0.0155，使用方风险质量p1为0.105。

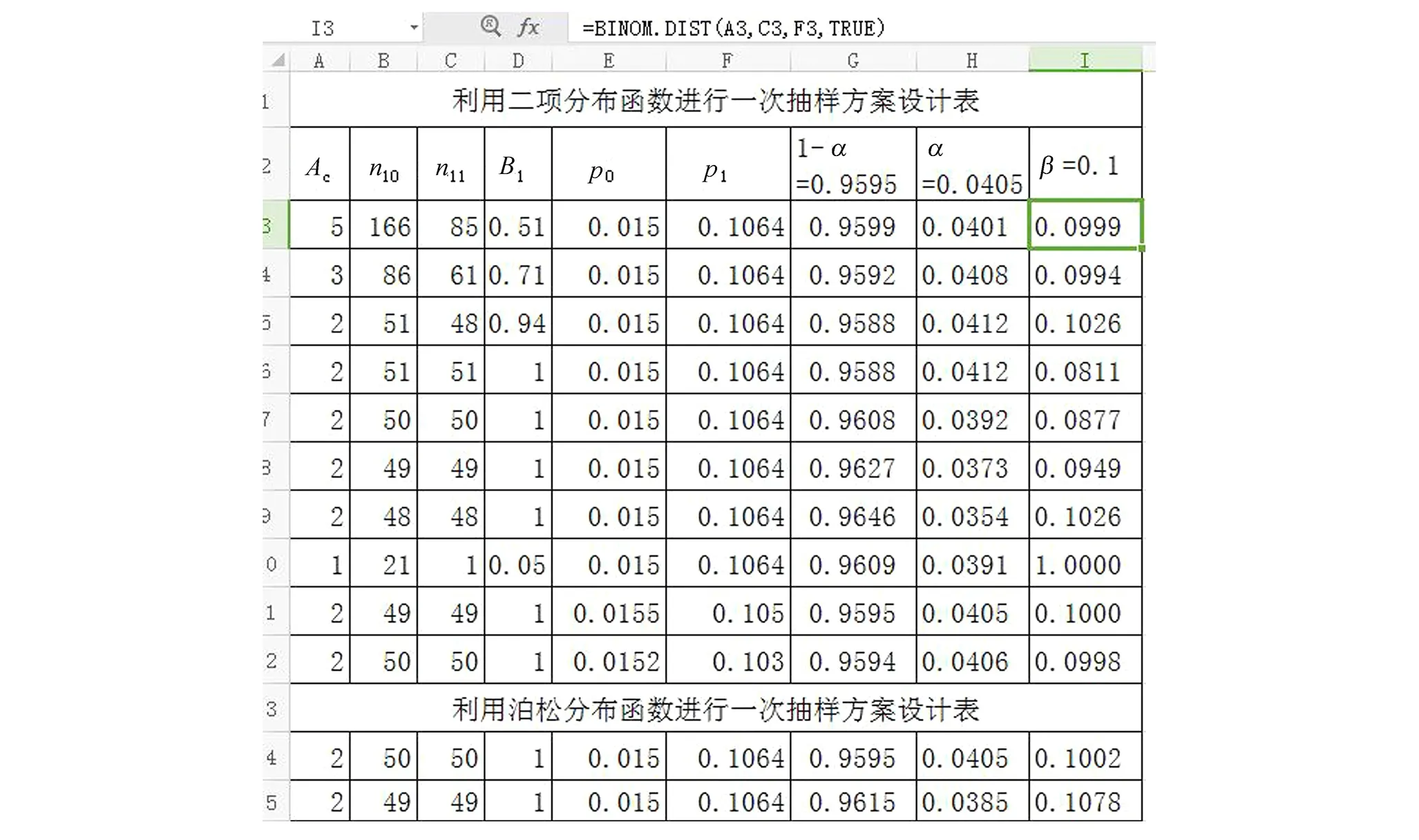
图1 一次抽样方案设计截图Fig.1 The screenshot of single sampling

B. 本批的不合格品件数D=15件，远小于样本量n=50件，因此本例不合格品出现的概率用服从二项分布求解是不合适的。本例不合格品出现的概率最好用服从超几何分布求解，但因超几何分布求解比较复杂，而p1为0.1064只稍超0.1，因此，本例不合格品出现的概率用服从泊松分布求解比较合适。

C. 如图1所示，不合格品出现的概率用服从泊松分布求解的结果为：Ac等于2，n1等于50，与不合格品出现的概率用服从二项分布求解的结果相似。本例用服从泊松分布求解的结果完全满足要求是因为本例取自GB/T2828.1国标中的一组数据，且在国标中就是以服从泊松分布求解的，这也有利于判断本文计算是否正确。

(2)二次抽样方案设计程序

下面仍以上述例子说明用excel表插入函数进行二次抽样方案设计的程序。

A.按表1规定确定接收概率分布函数。如上所述，本例选用泊松分布函数。

B.用excel表计算一次抽样方案

由上述计算可得一次抽样方案：Ac=2,n1=50

C.对二次抽样方案的某些参数进行估计

n2≈n1/1.55=32；0≤AC1≤2

1≤m1≤2； 0≤m2≤2;

D.设计excel表头

用excel表设计二次抽样检验方案的表头如图2所示。第3行及第4行为试算栏，第6行～第13行为结果栏。与生产方有关数据行表示的数据为λ20、p0、L0;与使用方有关数据的数据为λ21、p1、L1；

当m1=2时，计算接收概率有P0、P1、P2三列，对应的第2行取1、2；

E.试算

对AC1=0～2，m1=1～2，m2=0～2，逐项试算，若生产方风险α接近0.0405，使用方风险β接近于0.1,再改变样本量。几种较优设计方案如图2所示。

F.方案选择

从图2可见，当AC1=0、m1=2、m2=1、n2=32～39时, 均满足设计要求。

此时:Re1=AC1+m1+1=3;AC2=AC1+m1+m2=3;Re2=AC2+1 =4

此例二次抽样检验方案为：AC1为0、AC2与Re1为3、Re2为4、n2为32与39之间任意整数(以合同约定等为准)，若合同未约定，取中位数n2等于36。GB/T2828.1标准中,取n2取32,主要是考虑样本量的系列化及标准化。

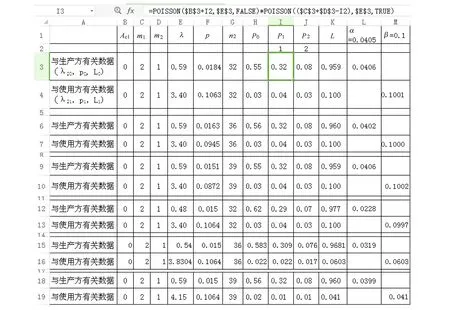
图2 二次抽样检验方案设计截图Fig.2 The screenshot of the secondary sampling

由于接收数AC1及AC2、拒收数Re1只能取整数，该解与要求有一定的差距。当n2等于32时，若保持风险质量p0为0.015及p1为0.1064不变，则生产方风险α为0.0228，使用方风险β为0.0997；若保持生产方风险α等于0.0405及使用方风险β等于0.1不变，则生产方风险质量p0为0.0184，使用方风险质量p1为0.1063，该方案对生产方有利。当n2等于39时，若保持风险质量p0为0.015及p1为0.1064不变，则生产方风险α为0.0399，使用方风险β为0.041；若保持生产方风险α等于0.0405及使用方风险β等于0.1不变，则生产方风险质量p0为0.0151，使用方风险质量p1为0.0872，该方案对使用方有利。当n2等于36时，若保持风险质量p0等于0.015及p1等于0.1064不变，则生产方风险α为0.0319，使用方风险β为0.0603；若保持生产方风险α等于0.0405及使用方风险β等于0.1不变，则生产方风险质量p0为0.0163，使用方风险质量p1为0.0945，该方案生产方及使用方利益均等。

5 结论

(1)利用excel表插入函数可以很方便地进行各种条件下的一次抽样检验方案及二次抽样检验方案的精准设计，克服了采用图或表设计时，在某些特殊要求下设计精度不够的问题;

(2)质量设计人员掌握了用excel表插入函数进行一次抽样检验及二次抽样检验方案设计方法，可了解国标GB/T2828系列标准中图或表数据来源，对更好地理解和应用GB/T2828系列标准进行超硬复合片的抽样检验方案设计是十分有益的。