结合Chirp信号的单向广播机制水下无线传感器网络时间同步算法

金彦亮,姚 彬,张晓帅

(上海大学通信与信息工程学院,上海200444)

水下无线传感器网络(underwater wireless sensor networks,UWSNs)是基于水声通信建立的一种传感器网络,典型的UWSNs三维结构如图1所示.水下无线传感器网络一般是由布放在海底或海中的传感器节点、水下中继节点、水上船基接收站、卫星及岸基站接收器等设施组成.水下传感器节点之间、水下传感器和水下中继站之间通过水声通信来实现信息交互,最后信息将汇集到水上船基接收站,再通过卫星通信等方式将信息传送出去.水下无线传感器网络在海洋开采、海洋监测、海洋军事等领域得到了广泛的应用.

图1 水下无线传感器网络三维示意图Fig.1 Three-dimensional schematic diagram of UWSNs

水下无线传感器网络的基础功能如定位、MAC(media access control)层退避算法、定时事件、数据融合等都离不开时间同步[11-12],因此水下传感器网络时间同步的研究也受到越来越多研究者的关注.一些传统的陆上无线传感器网络时间同步技术，如泛洪时间同步协议(flooding time synchronization protocol,FTSP)[3]、传感器网络时间同步协议(timing-sync protocol for sensor network,TPSN)[4]和参考广播同步(reference broadcast synchronization,RBS)[5]等算法取得了较好的时间同步性能,因为无线电在空气中的传播速度为光速,所以这些算法都没有将传播时延考虑在内.而UWSNs主要利用水声通信[6],传播速度约为1 500 m/s,1 km传播距离大概需要0.667 s.显然上述算法不能直接运用于水下时间同步.此外,UWSNs的时间同步面临另外一个巨大挑战,就是水下节点的移动性带来的传播时延变化,因此水下节点之间的水声传播时延就不能以恒定值来计算[7].

数年来,研究者们提出影响水下无线传感器网络时间同步的关键因素主要包括:节点的相对移动、水声传播速度低、传播时延的可变性等[8],为此一些经典的水下无线传感器网络时间同步算法已经被提出,如高延迟时间同步(time synchronization for high latency,TSHL)[9]、MU-Sync(a time synchronization protocol for underwater mobile networks,水下移动网络时间同步协议)[10]、多普勒时间同步(Doppler-based time synchronization,D-Sync)[11]、多普勒辅助时间同步(Doppler-assisted time synchronization,DA-Sync)[12],结合Chirp信号时间同步(combined Chirp signal time synchronization,CCS-Sync)[13]算法.TSHL算法是首个针对UWSNs提出的时间同步算法,但是没有考虑节点移动性带来的传播时延变化,而是以传播时延不变为前提,这显然不符合实际.MU-Sync算法将节点移动性带来的传播时延变化加入考虑范围,但是仅仅以来回双向传播时延的平均值代替单向传播时延,这种方式在节点变化速度较大时势必会带来较大的误差.D-Sync算法首次引入利用多普勒频移来获得UWSNs时间同步的方法,并在不同的环境下都表现出了较好的性能,但是D-Sync算法没有考虑到节点时间未同步的情况对多普勒规模因子估计的影响.DA-Sync算法在D-Sync算法的基础上提出利用正交频分复用(orthogonal frequency division multiplexing,OFDM)来估计多普勒规模因子,同时利用卡尔曼滤波器来提高相对移动速度的估计精度,但是DA-Sync算法是基于点对点模型提出的算法,在实际应用当中,随着节点规模的增大,势必会带来巨大的能量消耗.此外,DA-Sync算法虽然考虑了频偏对多普勒规模因子估计的影响,但是未考虑相偏带来的影响.CCS-Sync算法则引入Chirp信号以估计多普勒因子,并提出粗同步与细同步两个阶段处理时间同步,但是CCS-Sync算法与上述几种水下时间同步算法一样,都需要节点之间进行来回信息交互以实现时间同步,这势必会降低信道的吞吐率,当节点密度过大时,会导致信道阻塞.同时,CCS-Sync算法在估算多普勒频移因子时,也未考虑到相偏带来的影响.

在本工作提出的结合Chirp信号的广播时间同步(Chirp-based broadcasting time synchronization,CB-Sync)算法中,不同于DA-Sync与CCS-Sync算法只考虑了时钟频偏对多普勒规模因子估计的影响,而是在接收节点收到Chirp导频信号后,通过本地时间的时钟频偏和相偏来校正多普勒规模因子的估计值,以减少相对移动速度的估计误差带来的影响.同时,在CB-Sync算法中,只需要信标节点不断广播信号来同步周围的邻居节点,而无需接收节点的消息反馈以实现时间同步,这样不仅可以减少信道阻塞,还可以获得更高的能量利用率.为了减少节点相对移动带来的同步误差,接收节点通过两次线性回归得到频偏与相偏的初始值.对于多普勒频移带来的时钟同步误差,CB-Sync算法最后会通过最小梯度下降算法估算出频偏与相偏的最优解.仿真实验结果证明了CB-Sync算法的高精度与低功耗性能.

1 CB-Sync算法

1.1 时钟模型

水下传感器网络节点一般都是通过一个晶体振荡器得到时钟源,但是由于晶振本身就存在频偏与相偏,再加上水下环境的变化,导致不同节点的晶振频偏与相偏都存在一定偏差.假设当前的世界标准时间(universal time coordinated,UTC)是t,则节点的本地时间T可表示为

在水下传感器网络中,一般会选一个信标节点,以其本地时间作为整个网络的UTC参考时间,时间同步算法的最终目的就是求出每个节点相对于信标节点的θ和β值.

1.2 单向广播机制

如图2所示,CB-Sync算法的一个显著特点就是信标节点(beacon node)只采用单向广播机制来同步普通接收节点(ordinary node),而不需要接收节点的反馈信息,这样不仅可以减少信道的阻塞,还可以发送更少的消息以实现多个邻居节点的时间同步,得到更高效的能量利用率.

在CB-Sync算法中,将信标节点的本地时间t作为整个网络的参考时间.如图3所示,信标节点以时间间隔tr周期性广播消息,每个广播消息的数据包都会包含从信标节点发送出去的时间t2n-1.当普通接收节点收到广播消息后,会记录下接收到该消息的本地时间T2n.显然,节点的本地时间T2n与相对于信标节点的逻辑时间t2n的关系可表示为T2n=θt2n+β.

图2 CB-Sync同步模型Fig.2 CB-Sync synchronization model

图3 信标节点周期性广播消息Fig.3 Beacon node periodically broadcasts the message

1.3 多普勒规模因子的估计

如图4所示,在CB-Sync算法中使用Chirp信号作为广播消息的导频序列,其中信标节点发送的Chirp导频信号如图5(a)所示,S(t)由一串Ns个脉冲信号组成,其中第一个脉冲峰值到最后一个脉冲峰值的间距为ts.由于多径效应,在接收端,每个脉冲会出现不同的拖尾,普通接收节点上的接收机只需要检测主径上的峰值,设在接收机上检测第一个到最后一个脉冲峰值的间距是Ts.但是,在初始状态下,Ts只是不同节点未同步的时间,其相对于信标节点的时间实际是(Ts-β)/θ,因此多普勒规模因子的值应为

但是在初始状态下,每个节点首次收到广播消息时,θ和β的值都是未知的,这里首先设θ的初始值为1,β的初始值为0,之后每次收到信标节点的广播消息,都会以上一次计算得到的θ和β值来更新多普勒规模因子η.

图4 广播消息的帧结构Fig.4 Frame structure of the broadcast message

图5 Chirp导频信号结构Fig.5 Chirp pilot signal structures

1.4 频偏值θ 的估计

CB-Sync算法没有采用传统的信息交互机制来实现时间同步,而只采用单向广播机制来完成时间同步,主要是利用了普通接收节点在接收前后两次广播消息的时间间隔内的相对移动距离与频偏θ的关系,并通过两次线性回归以得到更高的同步精度.

首先,假设信标节点前后两次发送广播消息的时间分别是t2n-3和t2n-1,传播时延分别是τn-1和τn(见图2),则可以得到

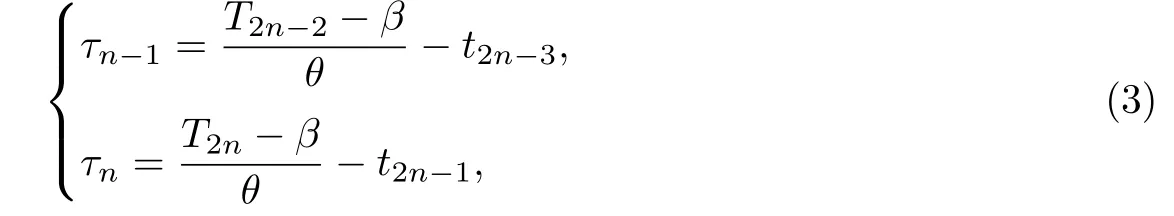
式中,n≥2.将上下式相减可得

此外,水声的传播速度c=1 500 m/s可以当作一个常数,从运动学角度可以得到

这里的A和B是为了方便表示,分别指信标节点和普通接收节点.令A在t2n-1时刻的坐标为PA(t2n-1),B收到广播信号的时刻是T2n,相对于A的实际时刻是t2n,这里dAB(t2n-1-t2n)= ‖PA(t2n-1)-PB(t2n)‖.

这样,就可以把式(4)转化为

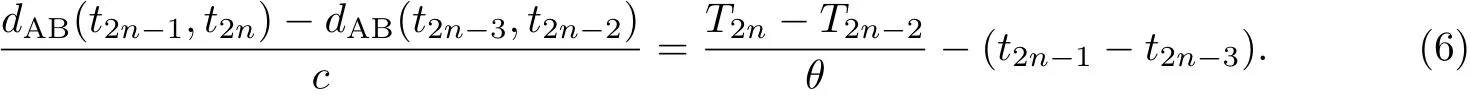
对式(5)再次修改可得

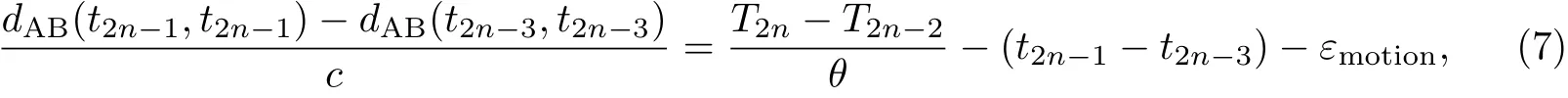
这里的εmotion表示由节点的移动性带来的相对误差,

进一步可以得到

式中,vAB表示节点A,B的平均移动速度.在水下传感器网络中,节点的最大移动速度一般不超过5 m/s.此外,由于在水下传感器网络中,节点之间的平均距离一般为1.5 km,故水下传播时延不会大于1 s,即τn-1,τn≤1 s,因此|εmotion|≤6 ms.至此可以证明,由节点移动性带来的相对移动误差是有界的,这样可以将εmotion看成一个未知常数.

由式(7)可以看出,只需求出dAB(t2n-1,t2n-1)-dAB(t2n-3,t2n-3)的值,再通过线性回归,即可弱化εmotion偏差求得频偏θ.

在t2n-3至t2n-1阶段,可以假设信标节点相对静止不动,因此节点B相对于节点A的移动距离即为dAB(t2n-1,t2n-1)-dAB(t2n-3,t2n-3).CB-Sync算法通过1.3节估计的多普勒规模因子η,可求得在t2n-3和t2n-1阶段的平均移动速度

式中,ηt2n-3和ηt2n-1分别表示多普勒规模因子η在t2n-3和t2n-1阶段的值.

通过式(10)可求得相对移动距离

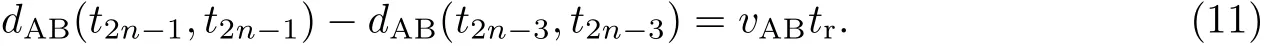
在初始状态下,CB-Sync算法首先通过收到的两次广播消息,根据式(7)得到频偏θ的初始值,之后每次收到的广播消息都会与上一次的广播消息组成一组线性回归的采样值更新频偏θ,同时每次收到的广播信息都会以上一次的频偏θ值更新式(2)得到新的多普勒规模因子η.

1.5 频偏θ 值的校正及相偏β 值的估计

在1.4节中,通过线性回归估计频偏θ的值时,将相对移动距离造成的误差εmotion当作常数计算.为了得到更高的时间同步精度,CB-Sync算法利用相对移动距离与传播时延之间的关系进行第二次线性回归以减少εmotion带来的误差.

首先将式(3)上下两式相加并结合式(4)可得

式中,n≥3.为了简化等式形式,令dAB(t2n-1)-dAB(t2n-3)=dAB(t2n-1,t2n-1)-dAB(t2n-3,t2n-3),对式(12)修改可得

可以根据式(13)构建另一个线性回归模型,以一组(t2n-3+τn-1,T2n-2)或者(t2n-1+τn,T2n)为坐标求出线性回归模型的斜率与截距,即为校正过的θ和β值.

1.6 最小梯度下降算法估计最终值

通过上述两次线性回归的方法得到的频偏θ和相偏β会受到预估的多普勒规模因子误差的影响,尽管可以通过迭代的方式来减小误差,但是并不能得到最优解.CB-Sync算法通过最小梯度下降算法来预估频偏θ的最优解,由于最小梯度下降算法存在最优解为极小值的情况,所以将两次线性回归方法得到的频偏θ和相偏β的值作为最小梯度下降算法的初始解,确保得到的最优解是最小值.

根据式(6),令λ=1/θ,可得

根据最小梯度下降算法,定义损失函数:

这样就可得到

式中,χ=T2n-T2n-2,α=1/(Nθ(0)),其中θ(0)就是通过两次线性回归得到的频偏的初始值.

2 仿真结果

下面将从不同的角度对比CB-Sync算法与CCS-Sync,DA-Sync,D-Sync,MU-Sync算法的性能.仿真过程中,在1 000 m×1 000 m×1 000 m的范围内随机散布29个普通接收节点并在中心位置部署一个信标节点.为了简化仿真,这里认为所有的普通接收节点都可以收到信标节点的广播消息.同时设置30个普通接收节点的初始频偏θ=80×10-6,相偏β=50×10-6s,信标节点发送广播消息间隔tr=6 s,Chirp导频包含的脉冲个数Ns=10,数据包固定长度为50 B.为了使仿真结果更加逼近真实环境数据,设置节点遵循文献[14]提出的水下节点经验运动模型:对应的运动参数如表1所示.

表1 节点运动参数Table 1 Parameters of node motion

图6是在网络中信标节点与每个普通接收节点之间消息总数是15时[13],所得到的平均每个普通接收节点的同步误差.可以看出,CB-Sync算法在同步完成以后,同步误差明显优于其他几种算法,主要原因有两方面:一方面,CB-Sync算法充分考虑了多普勒规模因子估计过程中普通接收节点与信标节点时间频偏与相偏不同步带来的估计误差;另一方面,CB-Sync算法以单向广播机制代替双向消息交互方式,节点在前后两次广播消息阶段的相对移动距离差可以看成普通接收节点相对于信标节点的相对移动距离差,从而可采用线性回归方法消除相对移动距离的误差,求得频偏的值,之后再根据传播时延建立的线性回归模型校正频偏值以及相偏值,最后利用最小梯度下降算法来弱化多普勒频移对时间同步误差带来的影响.

图6 同步误差随同步时间的变化Fig.6 Variation of synchronization error with synchronization time

为了得到单向广播机制与双向消息交互机制在不同网络规模上的同步误差性能比较,图7给出在不同的网络节点规模上[11],BD-Sync,D-Sync,DA-Sync,CCS-Sync与CB-Sync算法的比较,其中BD-Sync算法是基于D-Sync算法基础上的一种广播机制的改进,但不是完全的单向广播,在第一阶段仍然需要与邻居节点双向消息交互.从图7中可以看出,BD-Sync与CB-Sync算法随着网络规模的扩大都具有较为稳定的同步性能,但是D-Sync,DA-Sync算法都是以一对节点的时间同步为基础,随着网络节点数增多,同步性能都有明显的下降.CCS-Sync算法在第一阶段也是以节点的双向消息交互为基础,随着网络规模的扩大,同步性能也有所下降.从图5中可以看出,CB-Sync算法在网络规模较小时有较好的同步性能,并在节点数增多时,仍保持了较好的同步性能.

图7同步误差随网络节点数的变化Fig.7 Synchronization errors vary with the number of nodes in the network

图8 给出了各个算法的同步误差性能与信标节点和普通接收节点同步过程中消息总数的关系[12].从图中可以看出,对于每种算法,随着消息总数的增加,算法的同步误差都在减小,但是不同算法的误差下降幅度是不一样的.CB-Sync算法在消息总数小于20时,较其他算法有较好的同步性能;在消息总数大于25时,CB-Sync算法与其他算法的同步误差性能接近.换言之,CB-Sync较CCS-Sync,DA-Sync,D-Sync算法可以以更少的能量消耗得到更高的同步精度.

图8 同步误差随消息总数的变化Fig.8 Variation of synchronization error with the total number of the messages

为了比较不同算法的能量消耗,采用文献[12]定义的能量利用率

式中,k表示在时间ϑ秒内同步误差小于特定值时需要重新同步的次数,δ表示每次同步需要的消息总数,γ表示数据包的大小.从图9可以看出,当δ=15时,每个算法的同步误差都较明显,因此选择δ=15,ϑ=104s,γ=40 B.这样ρ就可以表示不同算法在保持一定的同步误差范围内需要的能量消耗.对于不同算法,同步误差要求越小,k值就越大,ρ值就越小.从图9中可以看出,CB-Sync算法相比于其他几种算法有更高的能量利用效率,说明CB-Sync算法在保持同步误差处于一定范围内时需要更少的再次同步次数.

图9能量消耗随同步误差的变化Fig.9 Variation of energy consumption with synchronization error

图10 给出了整个网络中所有节点能量消耗总和与节点数的关系[11].CB-Sync是一种广播机制的算法,它无需一次通过对单点的同步来达到整个网络所有节点的同步,每次广播消息不针对特定的节点,每个节点根据前后收到的广播消息来实现自身的时间同步,因此CB-Sync算法不会随着网络规模的增大而需要对每个节点实现一次信息交互,整个网络中的能量消耗也不会增加.

图10 能量消耗随网络节点数的变化Fig.10 Variation of energy consumption varies with the number of nodes in the network

3 结束语

本工作提出了一种在水下传感器网络中利用单向广播机制的时间同步算法CB-Sync.在CB-Sync算法中,以Chirp导频信号在节点未被同步状态下来估计多普勒规模因子,减少了时间同步误差带来的多普勒规模因子估计误差.同时,CB-Sync算法提出了只利用单向广播机制同步网络中的节点,这样的机制可以很好地减少信道阻塞.从仿真实验结果来看,CB-Sync算法在同步精度与能量利用效率上都优于其他算法.因为CB-Sync算法是一种集中式的同步算法,随着跳数的增加会有同步误差的积累,所以在今后的研究中,将主要利用分布式的思想解决水下传感器网络的时间同步问题.