一种改进的异步电机模型预测直接转矩控制方法

宋文祥,乐胜康,吴晓新,阮 毅

(上海大学机电工程与自动化学院,上海200444)

在交流电机高性能驱动场合中,矢量控制[1]和直接转矩控制[2-5]得到了广泛应用.这两种控制方法的不同之处在于,直接转矩控制是用转矩和磁链滞环控制器来直接控制电机的转矩和磁链,而矢量控制是通过控制电机定子电流的d-q轴分量来控制电机的转矩和磁链.所以直接转矩控制的动态性能要比矢量控制的动态性能好,但是直接转矩控制存在转矩脉动和开关频率不固定的问题[6-7].针对转矩脉动问题,文献[8]给出一种基于空间矢量调制的直接转矩控制方法,有效地减小了异步电机的转矩脉动.直接转矩中开关频率不固定问题的根本原因是采用了滞环控制器,而文献[6]采用一种新的转矩磁链控制器解决了这一问题.

模型预测控制(model predictive control,MPC)是一种非线性预测控制策略,处理非线性约束的适应能力较强,是利用给定的价值函数作为优化准则,使得控制极具灵活性[9].由于模型预测控制需要在线实时求解,对控制器的性能要求比较高,以往受制于微处理器的计算能力,使得模型预测控制在电机驱动领域鲜有实际应用[10-11].近年来,随着数字信号处理器的发展,使得模型预测控制应用于电机驱动领域成为可能.文献[12]最先将模型预测控制应用到电机驱动领域中.事实上,传统双离合变速器(dual clutch transmission,DCT)也被广泛解释为一种预测控制策略,但缺乏明确的预测模型和优化准则,只能粗略地预测下一步开关动作.

文献[13]给出一种长预测范围的模型预测直接电流控制方法,能够在保证电机运行性能的前提下显著降低逆变器的开关频率.文献[14]将有限控制集模型预测转矩控制和无差拍控制相结合,选择出最优的开关矢量,有效地改善了传统DCT的转矩性能.有限控制集模型预测转矩控制是一种利用系统离散模型来预测系统未来状态的控制方法,利用价值函数代替调制器以得到最优的开关矢量[15-17].文献[18]针对逆变器带阻感负载的电流控制,结合逆变器有限个开关矢量形成一种有限控制集MPC方法,取得了较为理想的控制效果.文献[19]基于有限控制集MPC思想,给出一种转矩预测控制方法,通过预测下一采样周期的磁链和转矩,以转矩纹波为价值函数,求解出最优的开关矢量和开关切换时刻,该方法能够有效地减小转矩脉动,但是会带来比较高的开关频率.

本工作给出了一种改进的模型预测直接转矩控制(model predictive direct torque control,MPDTC)方案,通过设计一种优化矢量选择器,可以得到给定电压矢量,然后判断给定电压矢量所处的扇区,从而获得需要进行价值函数优化求解的3个电压矢量.针对控制延时的影响,采用延时补偿控制来提高系统的控制性能.此外,为了降低逆变器的开关频率,在价值函数中加入对绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)开关切换次数的约束,形成了一种低开关频率模型预测直接转矩控制(low switching frequency model predictive direct torque control,LSFMPDTC)方法,能有效降低逆变器的开关频率.最后,通过仿真和实验对传统与改进的MPDTC性能作了对比评估.

1 异步电机数学模型

以电机定子磁链ψs和定子电流is为状态变量,两相静止α-β坐标系下的异步电机动态数学模型可表示为

式中: ψsα,ψsβ分别为定子磁链α,β 轴分量,isα,isβ分别为定子电流α,β轴分量,usα,usβ分别为定子电压α,β轴分量;Rs,Rr分别为定、转子电阻;Ls,Lr,Lm分别为定、转子电感和互感;ωr为转子转速;δ=LsLr-L2m.

定子磁链幅值与电磁转矩可分别表示为

式中,np为电机极对数,⊗表示叉乘.

2 传统模型预测直接转矩控制

2.1 控制系统结构

图1为传统模型预测直接转矩控制系统框图,图中IM表示感应电机(induction motor).与传统直接转矩控制相比,外环同样是转速环,通过比例积分(proportion integral,PI)调节器获得转矩的参考值.所不同的是,模型预测直接转矩控制的内环为模型预测控制器,代替了传统直接转矩控制中的磁链和转矩滞环.模型预测控制器由转矩和磁链的预测模型和价值函数构成,通过预测模型得到磁链和转矩的预测值,由价值函数评价出最优的开关矢量,最后将最优的开关矢量作用于逆变器.

图1 传统的模型预测直接转矩控制框图Fig.1 Block diagram of conventional MPDTC

2.2 全阶磁链观测器

磁链观测的精度会直接影响模型预测直接转矩控制系统的性能,为了提高磁链观测的精度,本工作将全阶磁链观测器引入控制系统中.所采用的全阶磁链观测器数学模型[20]如下:

其中b为负常数.

2.3 预测模型

前向欧拉离散化方法可以近似表示为

式中,Ts为系统的采样周期.

为了预测定子电流和定子磁链下一时刻的值,可采用式(9)的前向欧拉法对式(1)～(4)分别进行离散化,得到定子电流和定子磁链的预测模型如下:

将式(10)和(11)代入式(5)中,可得定子磁链幅值|ψs|的预测值为

将式(10)～(13)代入式(6)中,可得转矩Te的预测值为

对于两电平电压型逆变器来说,若在一个控制周期内只作用一个电压矢量,则总共有8个电压矢量u0,u1,···,u7可供选择.在逆变器第i个电压矢量的作用下,由式(14)和(15)可以得到预测的定子磁链幅值|(k+1)|和转矩(k+1).

2.4 价值函数优化

模型预测控制的价值函数具有灵活性和多样性,在直接转矩控制中,期望电机的转矩和磁链能够快速跟随其给定值[11],所以在模型预测直接转矩控制中,将磁链和转矩的相对偏差作为价值函数:

将式(16)作为价值函数,可以实现磁链和转矩快速跟随给定值,但是逆变器的开关频率较高,在中高压的驱动场合中,期望在保证控制性能的同时降低逆变器的开关频率.相应地,在价值函数中对开关切换次数进行约束,低开关频率模型预测直接转矩控制(LSFMPDTC)的价值函数可以表示为

式中,Sx(k)为当前时刻的开关状态,Sx(k-1)为前一时刻的开关状态,kf为IGBT开关切换次数的权重因子,通过增大kf的值可以有效降低逆变器的开关频率,但是不能一味增大,否则会出现电机失控的情况.

3 改进模型预测直接转矩控制

3.1 优化矢量选择器

改进的模型预测直接转矩控制方案的结构框图如图2所示,与传统模型预测直接转矩控制相比,增加了延时补偿环节和优化矢量选择器来提高控制系统的性能.

图2 改进的模型预测直接转矩控制框图Fig.2 Block diagram of improved MPDTC

考虑到两电平逆变器存在8个电压矢量,在价值函数优化过程中,需要对这8个电压矢量进行优化求解,这使得优化求解过程的计算量显著增加.为了降低优化求解的计算量,本工作设计了一种优化矢量选择器,通过定子磁链的给定值求得给定的电压矢量,使得在价值函数优化过程中只需对给定电压矢量所在扇区的3个电压矢量进行优化求解即可,有效降低了优化求解的计算量.下面对优化矢量选择器的设计过程进行详细描述.

电机的电磁转矩可以用定子磁链ψs和转子磁链ψr表示如下:

由式(18)可得定、转子磁链之间的角度关系为

式(18)～(20)中所用到的转子磁链矢量可由定子磁链和定子电流计算得到.

令ψsα(k+1)=,ψsβ(k+1)=,由式(10)和(11)可得参考电压矢量的α-β坐标分量为

3.2 延时补偿

图3是转矩预测控制原理示意图,其中实线为转矩的实际轨迹,虚线为转矩的预测轨迹.为了简化原理图,只给出3个电压矢量的转矩预测图形.图3(a)为理想情况下的转矩预测控制,在这种情况下控制器的计算时间非常短,可以忽略不计.最优电压矢量uop(k)在k时刻计算得到,并立即作用于逆变器.在实际应用中,由于控制器的计算能力有限,控制算法将耗费大量的计算时间,甚至是整个控制周期的时间.所以,在k时刻计算得到的最优电压矢量uop(k)要等到k+1时刻才作用于逆变器,而此时的电流采样值和定子磁链已经变为is(k+1)和ψs(k+1),这将使得控制系统始终存在一拍延时,导致定子电流在参考值附近振荡,增加了电流和转矩的纹波[21](见图3(b)).

为了解决这一拍延时的问题,需要在k时刻计算出k+1时刻的最优电压矢量uop(k+1),然后在k+1时刻作用于逆变器(见图3(c)).这就需要在k时刻以is(k+1)和ψs(k+1)为初始条件对定子电流和定子磁链再向前预测一次,得到k+2时刻的定子电流和定子磁链预测值is(k+2)和ψs(k+2):

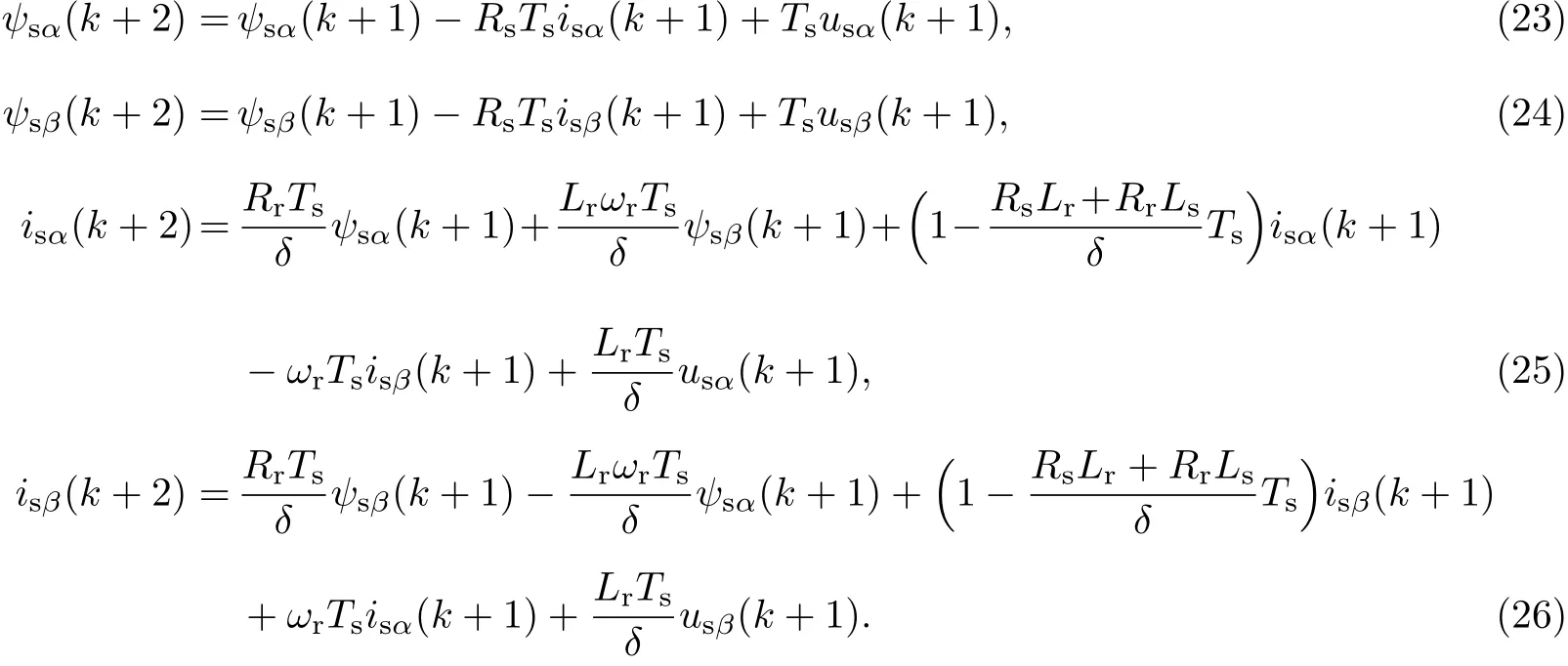
图3 转矩预测控制原理示意图Fig.3 Schematic diagrams of the torque predictive control

由式(5)和(6)可得定子磁链幅值和电磁转矩k+2时刻的预测值为

有延时补偿的MPDTC和LSFMPDTC的价值函数可以分别表示为

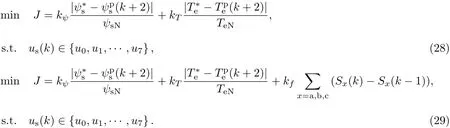
4 仿真结果

为了验证本工作提出的改进的MPDTC方法的正确性,利用Matlab/Simulink建立驱动系统的仿真模型进行仿真研究.仿真中MPDTC的磁链和转矩权重因子为kψ=2,kT=1,LSFMPDTC的权重因子为kψ=2,kT=1,kf=0.1,电机的额定值和相关参数如表1所示,系统采样频率为6 kHz,Udc为540 V.

表1 异步电机驱动系统相关参数Table 1 Parameters of induction machine drive system

图4给出了无延时补偿MPDTC、有延时补偿MPDTC与有延时补偿LSFMPDTC方法动态过程对应的定子电流、转速、定子磁链和转矩.仿真条件设定如下:电机空载起动,0.1 s转速给定阶跃突变为300 r/min(10 Hz),0.4 s时负载转矩突加至半载10 N·m,0.8 s转速给定阶跃突变为600 r/min(20 Hz),1.2 s时突加额定负载20 N·m,1.4 s转速给定阶跃突变为1 200 r/min(40 Hz),仿真时间2 s.从图中可以看出,加入延时补偿的MPDTC和LSFMPDTC的转矩和电流纹波显著减小,系统的稳态性能得到明显改善.此外,无论是在动态还是稳态过程中,估计的定子磁链^ψsα和实际的定子磁链ψsα非常一致.

图5给出了无延时补偿MPDTC、有延时补偿MPDTC与有延时补偿LSFMPDTC方法的定子磁链轨迹和幅值.从图中可以看出,无延时补偿MPDTC的定子磁链脉动大于有延时补偿MPDTC的定子磁链脉动,这说明加入延时补偿后能够有效减小磁链脉动.而有延时补偿LSFMPDTC的定子磁链脉动也大于有延时补偿MPDTC,这是由开关频率降低所引起的.

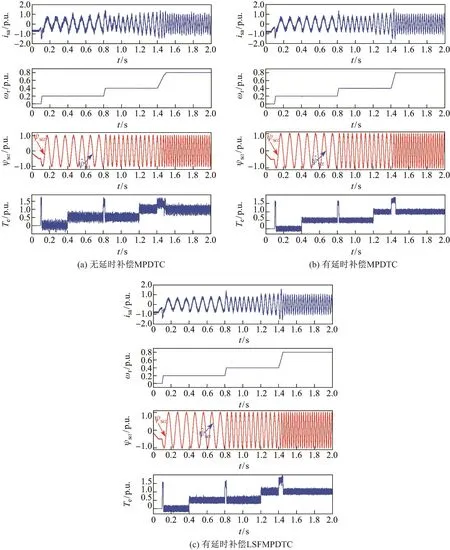
图4电机定子电流、转速、定子磁链和电磁转矩动态响应Fig.4 Dynamic responses of stator current,rotor speed,stator flux and electromagnetic torque

图6 给出了电机带额定负载运行在1 200 r/min时,无延时补偿MPDTC、有延时补偿MPDTC与有延时补偿LSFMPDTC方法对应的电流isa和逆变器电压ua的仿真结果.通过对比可以发现,有延时补偿LSFMPDTC的开关频率低于其他两种方法.通过对一段时间内的开关次数计数,可得到无延时补偿MPDTC平均开关频率为1.0 kHz,有延时补偿MPDTC为1.3 kHz,而有延时补偿LSFMPDTC则为900 Hz.

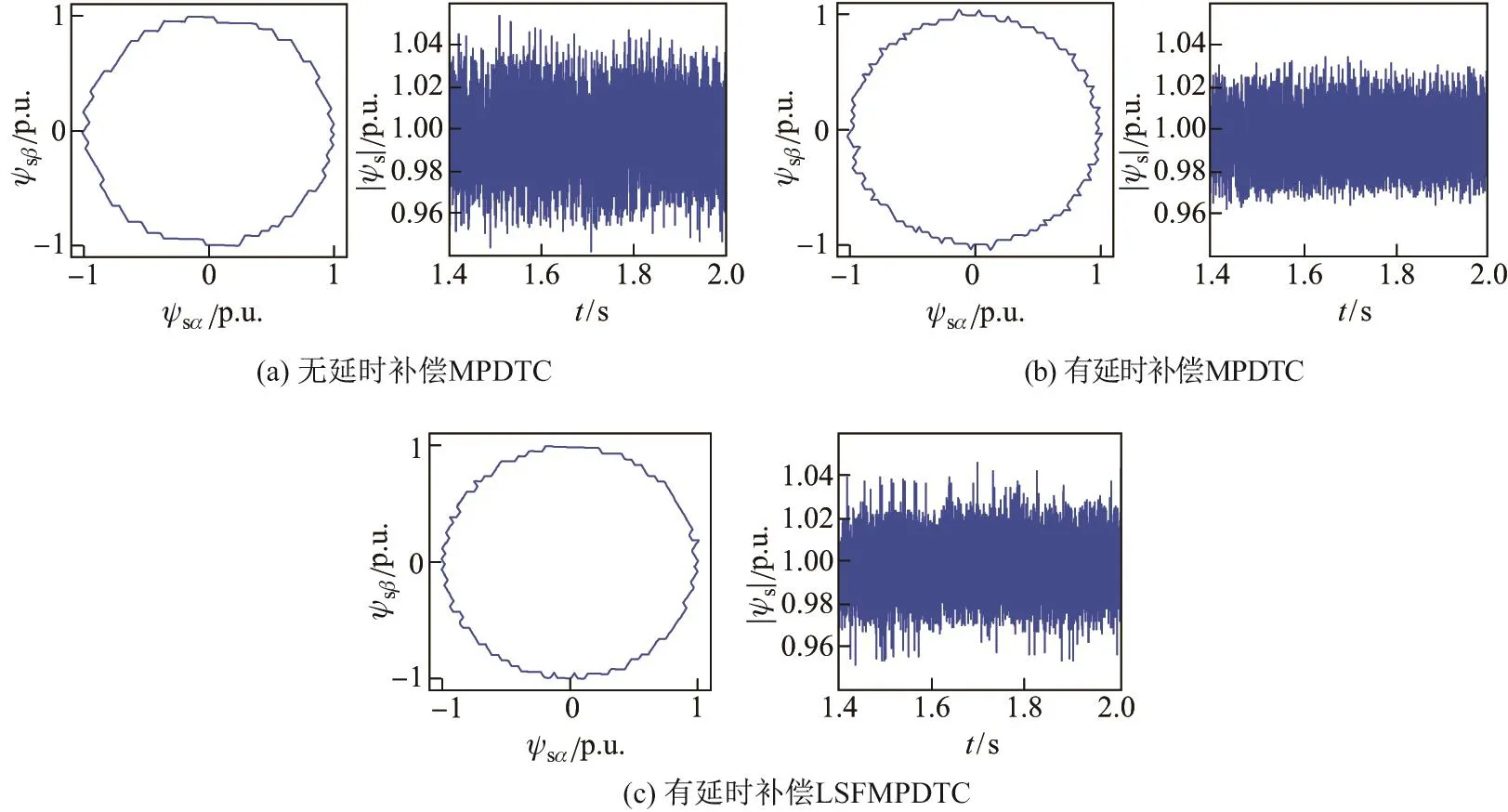
图5 三种控制方法的定子磁链轨迹和幅值Fig.5 Stator flux locus and amplitude of the three control methods

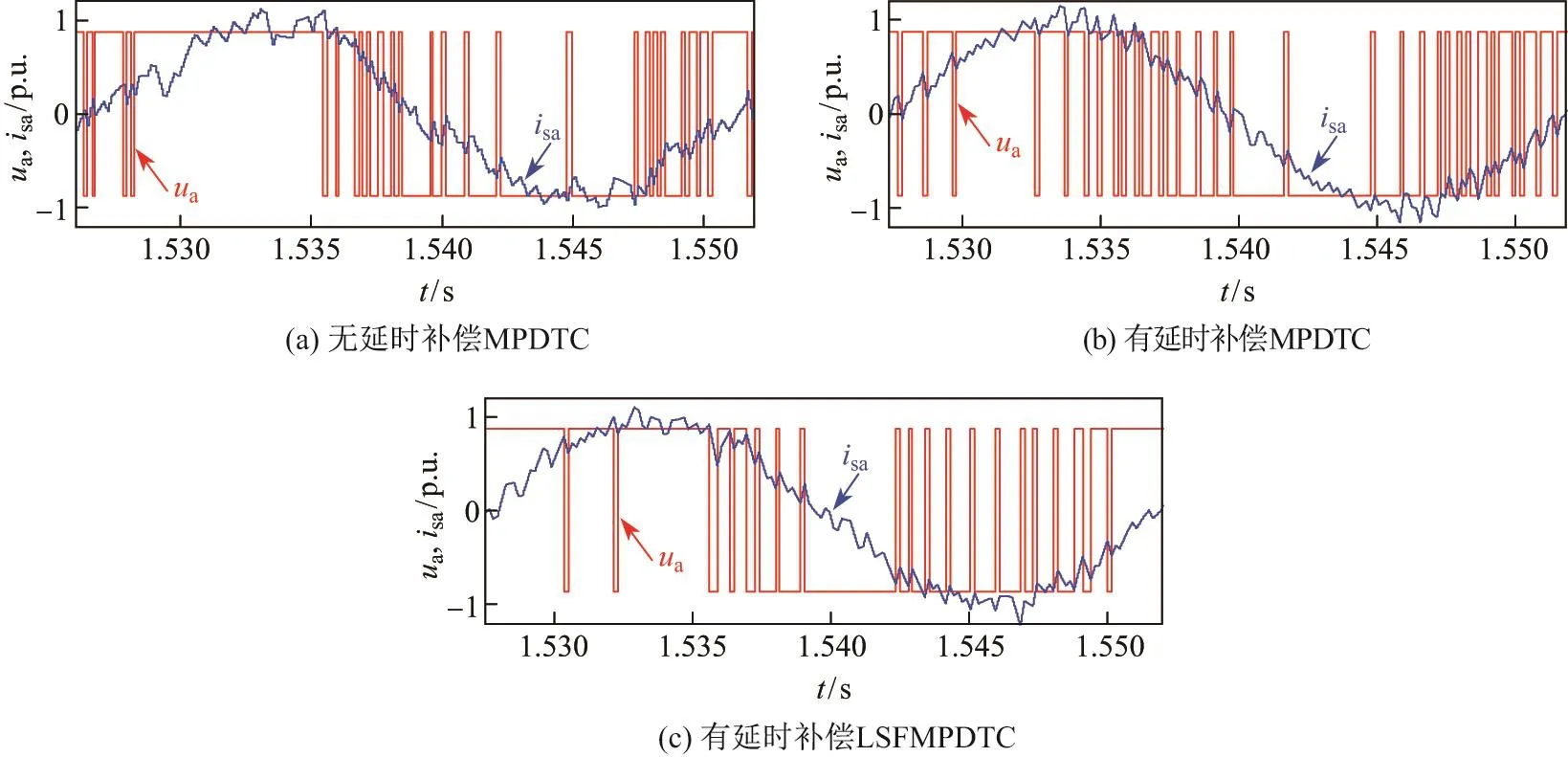
图6电机电流isa和逆变器电压uaFig.6 Current isaand inverter voltage uaof the machine

图7 为电机带额定负载运行在600 r/min时,3种不同开关频率权重因子kf作用下MPDTC的电流isa和逆变器电压uab.从图中可以清楚地看出,随着kf的增加,逆变器的开关频率在逐渐减小,与此同时,kf的增加会使得电机电流的纹波增大.图8进一步给出了不同权重因子kf对逆变器开关频率和电机电流畸变率的影响.在实际控制中,需要对逆变器的开关频率和电流畸变率进行折中考虑.

5 实验结果

图7 不同权重因子kf作用下的电流和逆变器电压Fig.7 Current and inverter voltage under different weighting factor kf

对本工作给出的控制方法进行实验验证,控制器采用TMS320F2812,系统采样控制频率设定为6 kHz,直流母线电压为540 V,电机参数与仿真采用的电机参数相同(见表1),实验中权重因子为kψ=3,kT=1,kf=0.14.

图9为电机运行在900 r/min时,突加和突减80%负载情况下,无延时补偿MPDTC、有延时补偿MPDTC和有延时补偿LSFMPDTC的定子磁链幅值|ψs|、转矩Te、转速n和电流isa.由图可以看出,有延时补偿MPDTC与LSFMPDTC的转矩脉动明显小于无延时补偿MPDTC的转矩脉动.3种控制方法的定子磁链幅值|ψs|在负载扰动时有微小的下降,而转速基本没有变化.

图10是无延时补偿MPDTC和有延时补偿MPDTC方法在电机带80%额定负载运行于900 r/min时的性能对比.左半部分为无延时补偿MPDTC的结果,右半部分则为有延时补偿MPDTC的结果.从图中可以发现,有延时补偿MPDTC的电流和转矩纹波较小,明显改善了电机运行性能.

图11(a)为电机运行在300 r/min时,突加和突减50%额定负载情况下,有延时补偿LSFMPDTC的实验结果;图11(b)为稳态运行时的实验结果.由图可以看出,在突加和突减负载时,定子磁链幅值和转速几乎都没有变化.在稳态运行时,转矩和电流的性能也都比较良好.

图9 突加与突减负载时3种方法实验结果Fig.9 Experimental results of three methods with a step load disturbance

当电机运行在900 r/min时,无延时补偿MPDTC、有延时补偿MPDTC和有延时补偿LSFMPDTC所对应的电流isa和逆变器电压ua如图12所示.可以明显发现,有延时补偿MPDTC的开关频率要比无延时补偿MPDTC和有延时补偿LSFMPDTC的开关频率高.无延时补偿MPDTC的平均开关频率为1.1 kHz,而有延时补偿MPDTC和LSFMPDTC的平均开关频率则分别为1.8和1.0 kHz.

6 结束语

本工作提出的改进的模型预测直接转矩控制方法,通过优化矢量选择器得到需要进行价值函数优化控制的3个电压矢量,可有效降低模型预测直接转矩控制的优化计算量.对于控制延时对系统性能的影响,延时补偿控制能够显著减小由控制延时引起的电流纹波和转矩脉动.通过在MPDTC的价值函数中加入开关切换次数的约束,增大开关频率的权重因子可降低逆变器的开关频率,但同时会使得电流畸变率有所增加.仿真和实验结果表明,由全阶磁链观测器得到的磁链能够准确地跟踪其给定值,改进的MPDTC具有良好的动、静态性能,并且可以有效降低逆变器的开关频率.

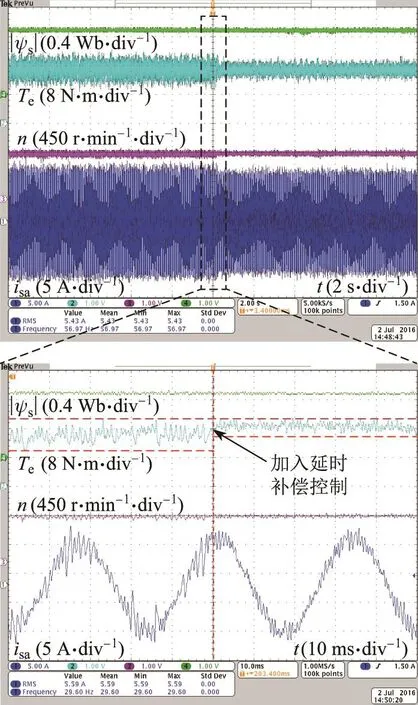
图10 有/无延时补偿的MPDTC实验结果对比Fig.10 Experimental results comparison between the MPDTC without delay compensation and the MPDTC with delay compensation

图11 有延时补偿LSFMPDTC的实验结果Fig.11 Experimental results of the LSFMPDTC with delay compensation

图12 逆变器电压ua和电流isa的实验结果Fig.12 Experimental results of the inverter voltage uaand the current isa