考虑桩-土相互作用的单支座脱空对桥墩受力性能的影响

王 帅 帅

(长安大学 公路学院, 陕西 西安 710064)

因简支变连续梁桥结构简单、施工方便,且具有连续梁和预制梁批量生产等优点[1-2],在山区高速公路中被广泛应用.支座是连接桥梁上、下部结构的重要部件,能够将上部结构的力传递给墩台,在活载作用下有良好的弹性以适应梁端的转动、较大的剪切变形用以满足主梁的水平位移.但桥梁在施工和运营中,支座会出现脱空、剪切变形过大、倾斜、开裂等病害,桥梁结构的受力随之改变,引起更多结构性的病害[3].

S.H.Kim等[4]通过对多跨简支梁桥动力性能的研究,分析桥梁在支座损坏前后的动力性能,发现支座损坏对桥梁整体的抗震性能有较大影响;胡峰强等[5]分析了支座脱空和支座活动方向异常对桥梁结构受力的影响,发现支座脱空对支反力影响较大;梁启元[6]通过对比设计汽车载荷及超载汽车载荷作用下支反力的变化,得出车辆超载严重导致支座脱空的结论,并提出采取加大支座间距、更换支座的整治措施;吴玉财等[7]依据高速公路桥梁病害调查结果,从设计、加工、施工和运营等方面对板式橡胶支座病害类型及原因进行分析,提出相应的处治对策.

综上所述,国内外专家对支座脱空进行了一系列的研究,也取得了重要的成果.但是,以往的研究大多集中在支反力、上部结构内力变化和脱空的原因分析及处治措施上,针对支座脱空对桥墩受力性能影响的研究相对较少.下部边界条件对于桥墩受力有一定影响,为了更接近实际,需考虑桩-土相互作用.由于支座脱空后支反力变化较大,下部结构的受力性能也随之改变.因此,本文结合桩-土相互作用,以单支座脱空为对象分析其对桥墩受力性能的影响.

1 工程概况

根据T形梁桥设计通用图,分别选择单孔标准跨径lb为20 m和30 m的一联简支变连续梁桥为研究对象,桥面横坡为双向2%,纵断面纵坡为2%,载荷等级为公路-I级.上部结构采用全预应力混凝土T梁,桥面连续,采用C50混凝土;下部结构采用双柱式墩,墩台为桩基础,采用C30混凝土.桥宽12 m,每跨由5片主梁组成,T梁间距2.45 m,中梁预制宽度1.8 m,湿接缝宽0.65 m.为了分析方便,下部结构均采用相同的尺寸.全桥立面布置见图1,上部结构跨中横断面如图2所示.

按照梁格法的理论,以实际截面模拟主梁和横隔板,由于横隔板纵向间距较大,所以需要采用虚拟横梁将各主梁连接在一起[8-9].其中:主梁取单片T梁;横隔板为实际尺寸;虚拟横梁宽度由单元划分大小来确定,厚度为主梁截面翼缘板的厚度.利用桥梁专用有限元软件MIDAS/Civil建立桥梁上部结构空间模型.

图1 桥梁立面布置图(单位:cm)Fig.1 Elevation layout of the bridge(unit:cm)

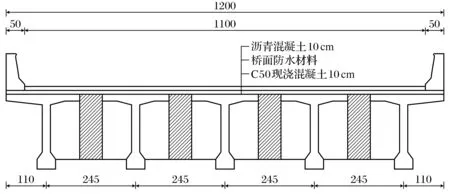
图2 主梁跨中横断面图(单位:cm)Fig.2 Cross-section profile in mid-span of main girder(unit:cm)

全桥均采用板式橡胶支座,其中两端伸缩缝位置处为四氟滑板支座,支座尺寸根据设计图纸确定,横桥向一排共5个支座,为分析方便,把①②③排支座记为A、B、C,支座布置如图3所示.支座脱空主要体现在支座与梁底脱离接触,引起旁边支座受力发生变化,主要是由于梁靴坡度设计有偏差及主梁在预应力及混凝土的收缩徐变作用下上拱造成的[10].通过解除脱空处的约束进行模拟.

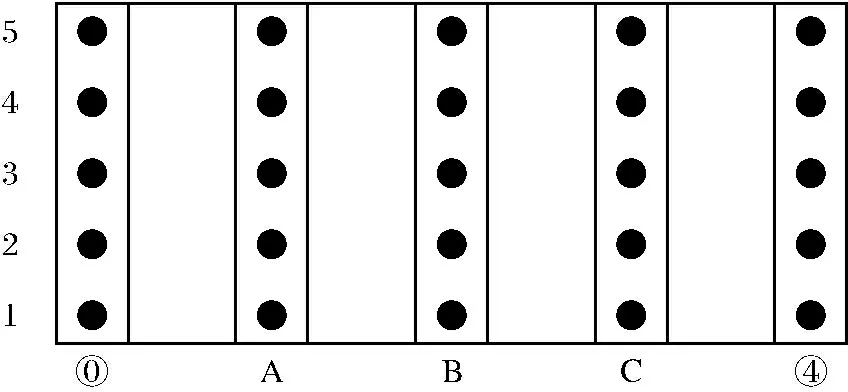
图3支座布置图
Fig.3 Arrangement plan of bearings

2 墩顶载荷分析

(1) 恒载荷. 主要考虑预制主梁、湿接缝、现浇连续段自重和桥面2期铺装载荷.

(2) 汽车载荷. 定义标准车辆载荷为在最不利的情况下, 从边梁处开始横桥向定义2个外偏车道, 并以影响线加载的方式进行移动载荷分析.

由于支座脱空后,支反力重新分布,此时墩身处于偏压状态.主要考虑上部结构恒载及汽车载荷作用下,各支座所受到的竖向反力.由于C排墩顶荷载与A排墩相同,因此只对A排、B排墩顶载荷进行分析,单孔标准跨径lb为20 m和30 m时梁桥各支座脱空前后竖向反力的结果如表1～表4所示.

综合来看,支座脱空后,支反力变化较大.中梁支座脱空后相邻支座的支反力均在正常值的1.3倍以上,边梁支座脱空后相邻支座的支反力均在正常值的1.8倍以上,因此边梁支座脱空比中梁支座脱空更危险,脱空处的相邻支座反力与正常情况相比增加得更多.

表1 A排单支座脱空前后竖向反力值(lb=20 m)Table 1 Vertical reaction force value before and after row A one bearing separation(lb=20 m) kN

表2 B排单支座脱空前后竖向反力值(lb=20 m)Table 2 Vertical reaction force value before and after row B one bearing separation(lb=20 m) kN

表3 A排单支座脱空前后竖向反力值(lb=30 m)Table 3 Vertical reaction force value before and after row A one bearing separation(lb=30 m) kN

表4 B排单支座脱空前后竖向反力值(lb=30 m)Table 4 Vertical reaction force value before and after row B one bearing separation(lb=30 m) kN

3 下部结构模型建立

利用国内外岩土工程界最常使用的软件ABAQUS建立下部结构实体模型,包括桩基、土体、系梁、墩柱、盖梁及垫石.桩基直径D=2 m,桩长L=23 m,墩身高H1=20 m,H2=27 m;土体考虑边界条件的影响,长、宽、高均取50 m.混凝土采用的是线弹性模型,土体采用的是Mohr-Coulomb模型,具体参数值见表5和表6.

表5 混凝土力学模型参数Table 5 Mechanical model parameters of concrete

表6 土体力学模型参数Table 6 Soil mechanics model parameters

土体的边界条件为:约束YZ面上X方向的水平位移;约束XZ面Y方向的水平位移;约束底面Z方向的位移.网格遵循疏密合理、收敛速度快的原则进行划分,模型均采用三维实体单元C3D8R(8节点6面体2次缩减积分单元).由于桩-土间存在相对滑移致变形不协调,故采用库仑摩擦模型模拟桩-土相互作用,可以较好地反映桩-土间的相互作用机理,其余部件不发生相对滑移,共同受力变形,故采用绑定约束[11-12].其中A排桥墩下部结构的计算模型立面图如图4所示.

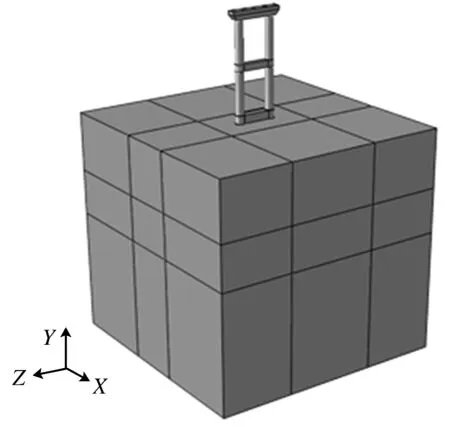
图4 下部结构的计算模型立面图Fig.4 Elevation diagram of calculation model for substructure

根据实际情况,计算得到的墩顶载荷以竖向均布力的形式作用在垫石上,垫石尺寸为0.6 m×0.6 m×0.1 m.为了分析盖梁各截面的弯矩值,从最外侧支座中心开始,将盖梁沿着横桥向每1.225 m分隔开;将墩身从下到上每2 m分隔开,以备输出各控制位置的弯矩和位移.

4 考虑桩-土作用前后的误差分析

以单孔标准跨径30 m的简支变连续梁桥为对象,在考虑桩-土作用与不考虑桩-土作用2种情况下,通过对比盖梁弯矩、墩身弯矩和墩身横向偏位的误差绝对值,分析桩-土作用对桥墩受力性能的影响.为了分析方便,定义行车方向右侧为外墩身,左侧为内墩身.

根据图5～图9的误差值分析发现:盖梁各截面弯矩在考虑桩-土作用和不考虑桩-土作用2种情况下的误差较小,最大误差仅为2.7%;墩身弯矩存在较大的误差,内、外墩身在考虑桩-土前后的最大误差分别达到1070%和881%;墩身横向偏位的误差均在50%以上.同样,对其他条件下桥墩受力性能差异的分析可以得到相同的结论.因此,为了更好地模拟实际情况下桥墩的受力情况,应该考虑桩-土作用的影响.

图5 考虑桩-土前后A排桥墩盖梁截面弯矩误差值Fig.5 The cover beam cross section bending moment error of piers of row A before and after considering the pile-soil

图6 考虑桩-土前后A排桥墩外墩身截面弯矩误差值Fig.6 The moment error of the external section of piers of row A before and after considering the pile-soil

图7 考虑桩-土前后A排桥墩内墩身截面弯矩误差值Fig.7 The moment error of the inner pier section of piers of row A before and after considering the pile-soil

图8 考虑桩-土前后A排桥墩外墩身横向偏位误差值Fig.8 The transverse deviation error of external piers of row A before and after considering the pile-soil

5 支座脱空对桥墩受力性能的影响

5.1 支座脱空对盖梁弯矩的影响

通过盖梁各截面处绕纵桥向的弯矩值变化,分析不同支座脱空对盖梁的影响.

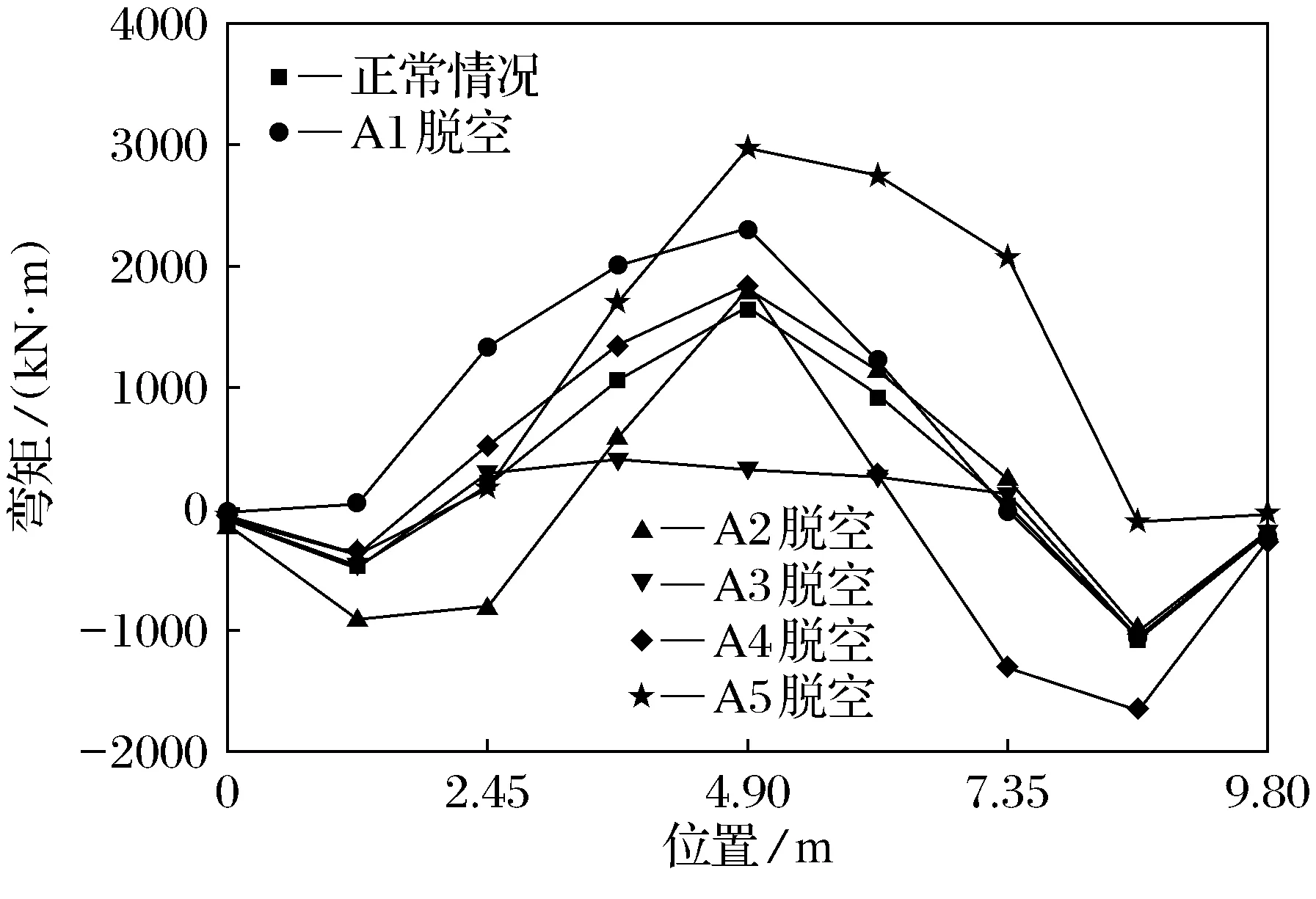
图10 A排桥墩盖梁截面弯矩图(lb=20 m)Fig.10 Cover beam cross section bending moment of piers of row A(lb=20 m)

图11 B排桥墩盖梁截面弯矩图(lb=20 m)Fig.11 Cover beam cross section bending moment of piers of row B(lb=20 m)

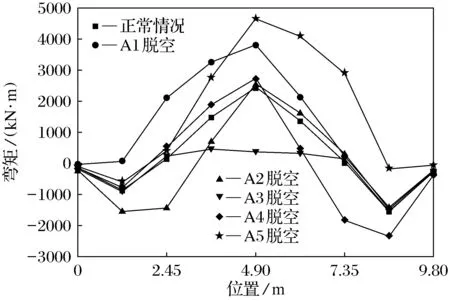
图12 A排桥墩盖梁截面弯矩图(lb=30 m)Fig.12 Cover beam cross section bending moment of piers of row A(lb=30 m)

图13 B排桥墩盖梁截面弯矩图(lb=30 m)Fig.13 Cover beam cross section bending moment of piers of row B(lb=30 m)

从图10～图13可以看出,不同支座脱空后,盖梁各截面弯矩变化规律基本相同,边梁支座脱空对弯矩的影响范围最大且均超出正常值.跨中截面处的弯矩达到最大值,其中A1、A5脱空,弯矩值分别超出正常值的35%和75%以上;B1、B5脱空,弯矩值同样分别超出正常值的35%和75%以上.

5.2 支座脱空对墩身弯矩的影响

通过墩身各截面处绕纵桥向的弯矩值变化,分析不同支座脱空对墩身的影响.

从图14～图17可以看出,A排不同支座脱空后,外墩柱、内墩身各计算截面处的弯矩变化规律基本相同,边梁支座脱空对弯矩的影响最显著,尤其是在横系梁上侧的墩身;而其余支座脱空后的弯矩值大小均接近甚至小于正常值.墩身顶面弯矩值最大,其中A1、A5脱空,外墩身弯矩值分别超出正常值的95%和150%以上,内墩身弯矩值则分别超出正常值的95%和240%以上.

图14 A排桥墩外墩身截面弯矩图(lb=20 m)Fig.14 External pier cross-section bending moment of piers of row A(lb=20 m)

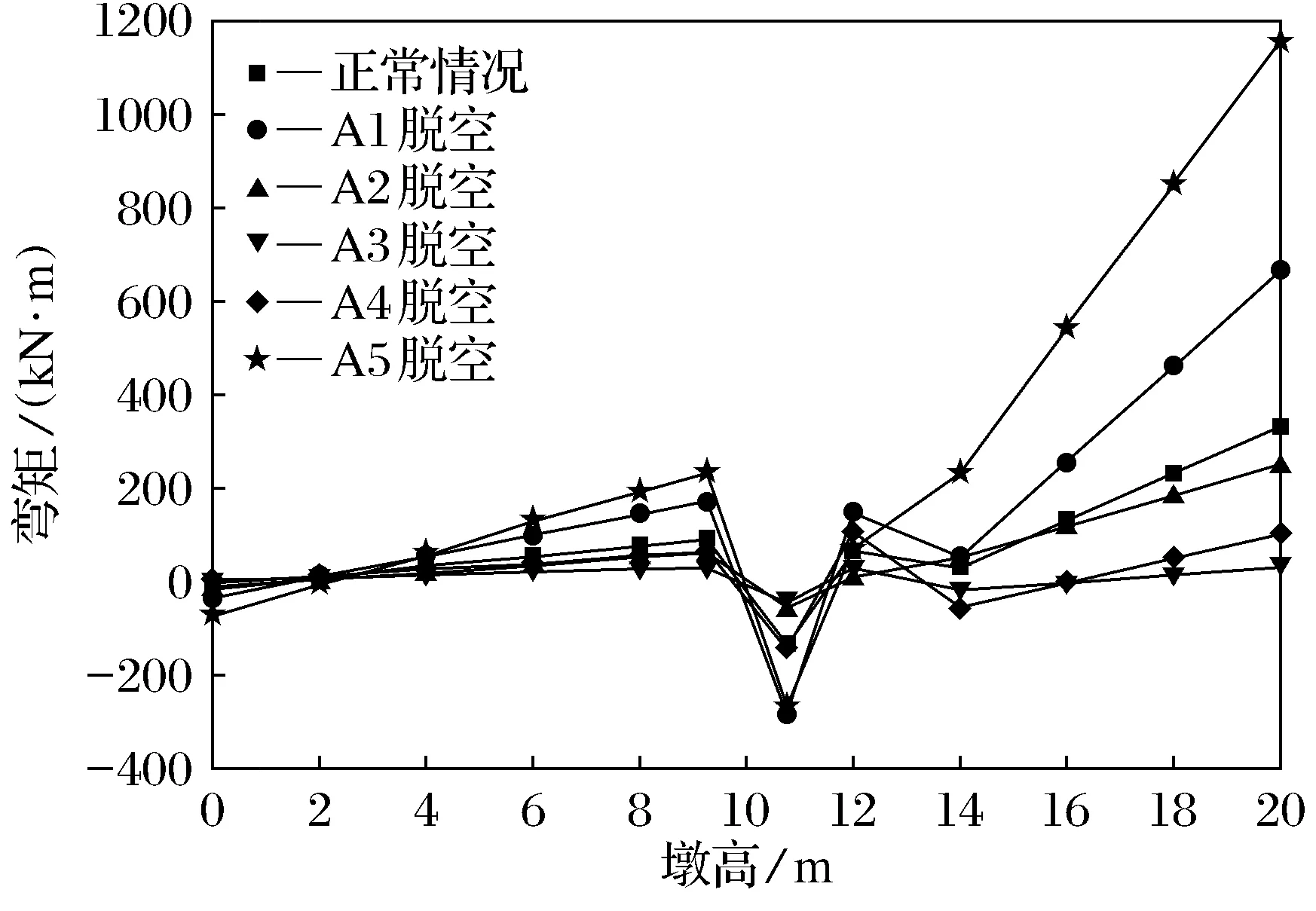
图15 A排桥墩内墩身截面弯矩图(lb=20 m)Fig.15 Inner pier cross-section bending moment of piers of row A(lb=20 m)

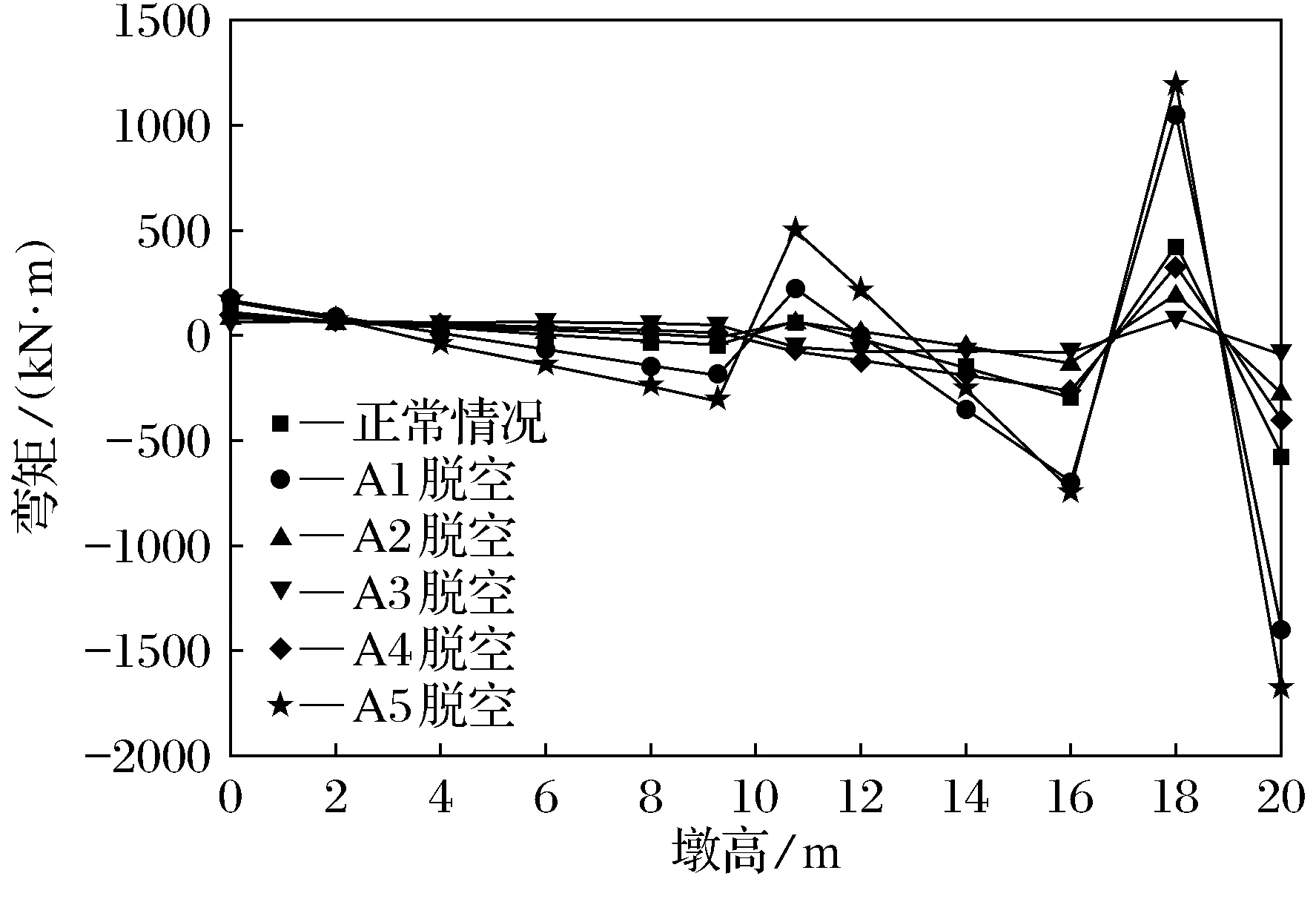
图16 A排桥墩外墩身截面弯矩图(lb=30 m)Fig.16 External pier cross-section bending moment of piers of row A(lb=30 m)

图17 A排桥墩内墩身截面弯矩图(lb=30 m)Fig.17 Inner pier cross-section bending moment of piers of row A(lb=30 m)

从图18～图21可以看出,B排不同支座脱空后,外墩身、内墩身各计算截面处的弯矩变化规律基本相同,边梁支座脱空对第1道横系梁上侧的墩身弯矩的影响最显著;而其余支座脱空后的弯矩值均接近甚至小于正常值.墩身顶面弯矩值最大,其中B1、B5脱空,外墩身弯矩值分别超出正常值的80%和145%以上;内墩身弯矩值则分别超出正常值的85%和230%.

图18 B排桥墩外墩身截面弯矩图(lb=20 m)Fig.18 External pier cross-section bending moment of piers of row B(lb=20 m)

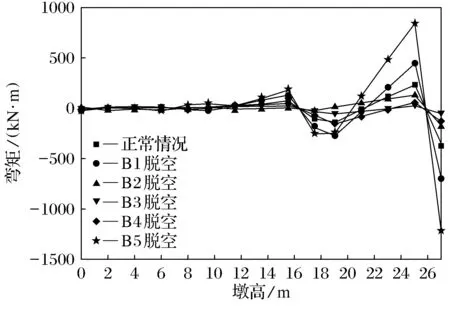
图19 B排桥墩外墩身截面弯矩图(lb=20 m)Fig.19 Inner pier cross-section bending moment of piers of row B(lb=20 m)

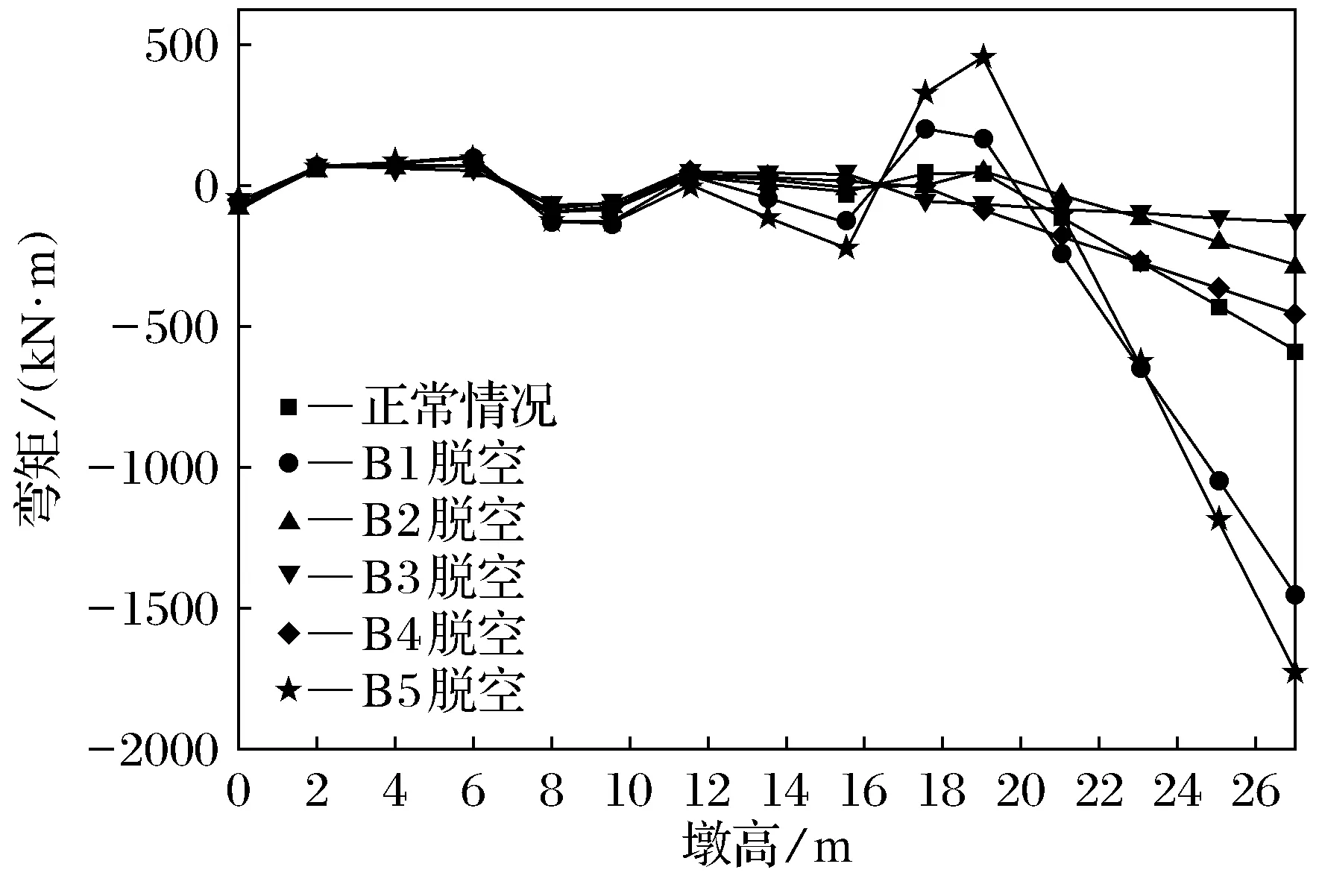
图20 B排桥墩外墩身截面弯矩图(lb=30 m)Fig.20 External pier cross-section bending moment of piers of row B(lb=30 m)

图21 B排桥墩外墩身截面弯矩图(lb=30 m)Fig.21 Inner pier cross-section bending moment of piers of row B(lb=30 m)

5.3 支座脱空对墩身横向偏位的影响

从图22～图29可以看出,不同支座脱空,A排和B排桥墩外墩身横向偏位、内墩身横向偏位的变化规律基本相同,A排桥墩外墩身在横系梁上方一定范围内,横向偏位的程度减缓甚至下降;B排桥墩外墩身在第1道横系梁上方处也存在相同的现象;内墩身横向偏位与外墩身相反.内边梁支座脱空对内墩身横向偏位影响最大,此时A排和B排桥墩内墩身顶部横向偏位值均达到最大值,但总体来看与正常值相差不大.

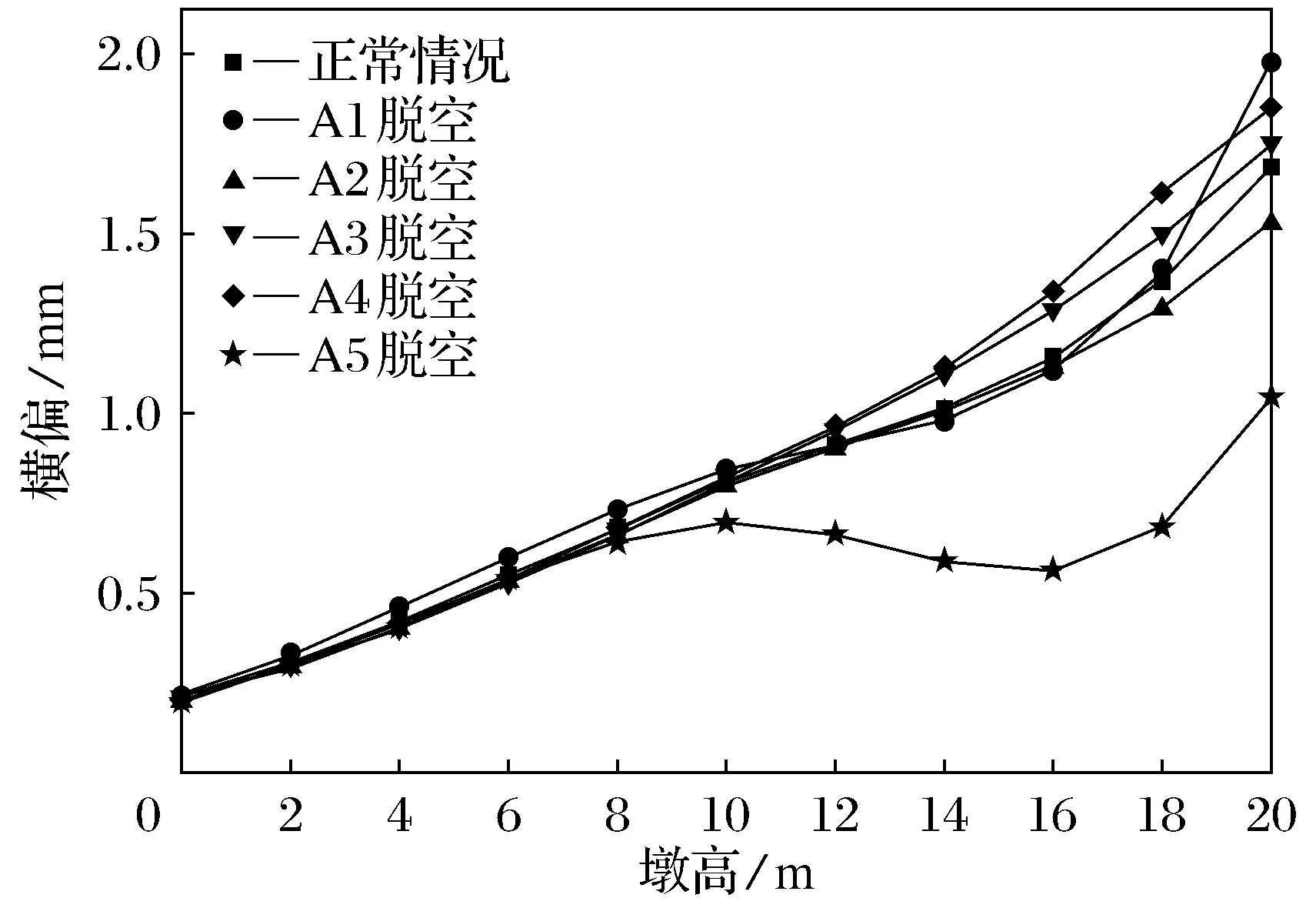
图22 A排桥墩外墩身横向偏位图(lb=20 m)Fig.22 External pier transverse deviation of piers of row A(lb=20 m)

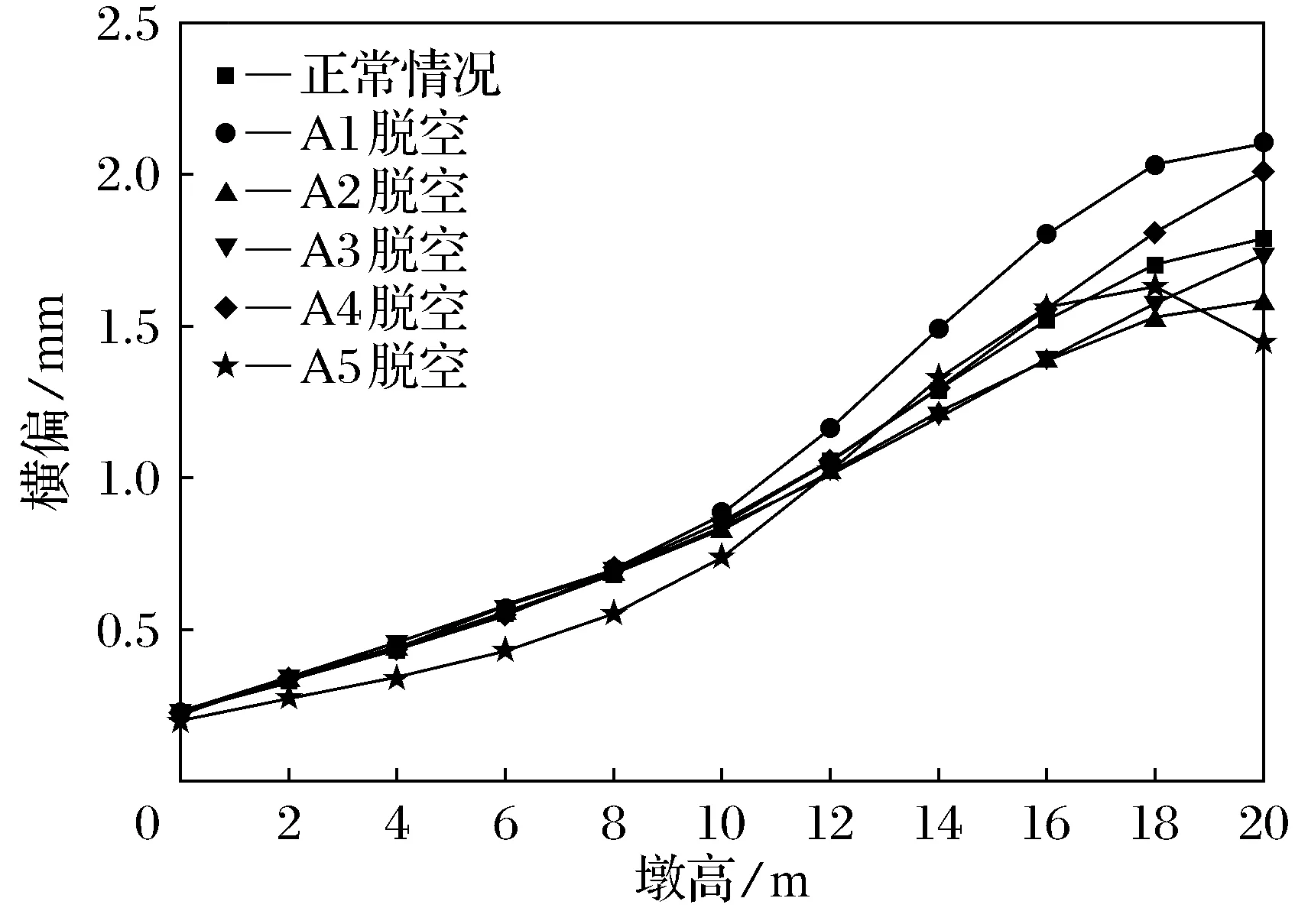
图23 A排桥墩内墩身横向偏位图(lb=20 m)Fig.23 Inner pier transverse deviation of piers of row A(lb=20 m)

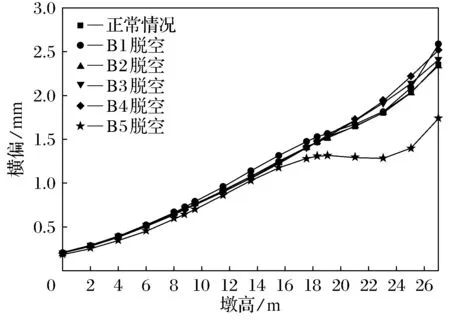
图24 B排桥墩外墩身横向偏位图(lb=20 m)Fig.24 External pier transverse deviation of piers of row B(lb=20 m)

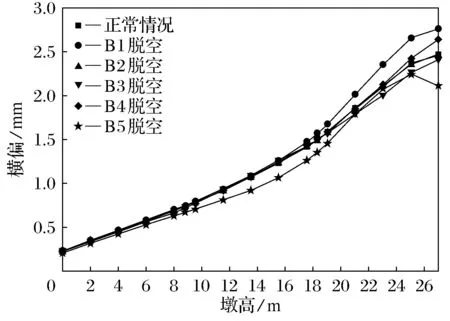
图25 B排桥墩内墩身横向偏位图(lb=20 m)Fig.25 Inner pier transverse deviation of piers of row B(lb=20 m)

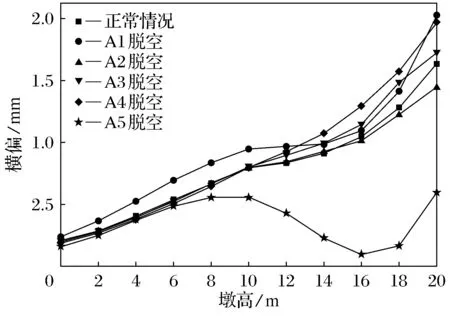
图26 A排桥墩外墩身横向偏位图(lb=30m)Fig.26 External pier transverse deviation of piers of row A(lb=30 m)

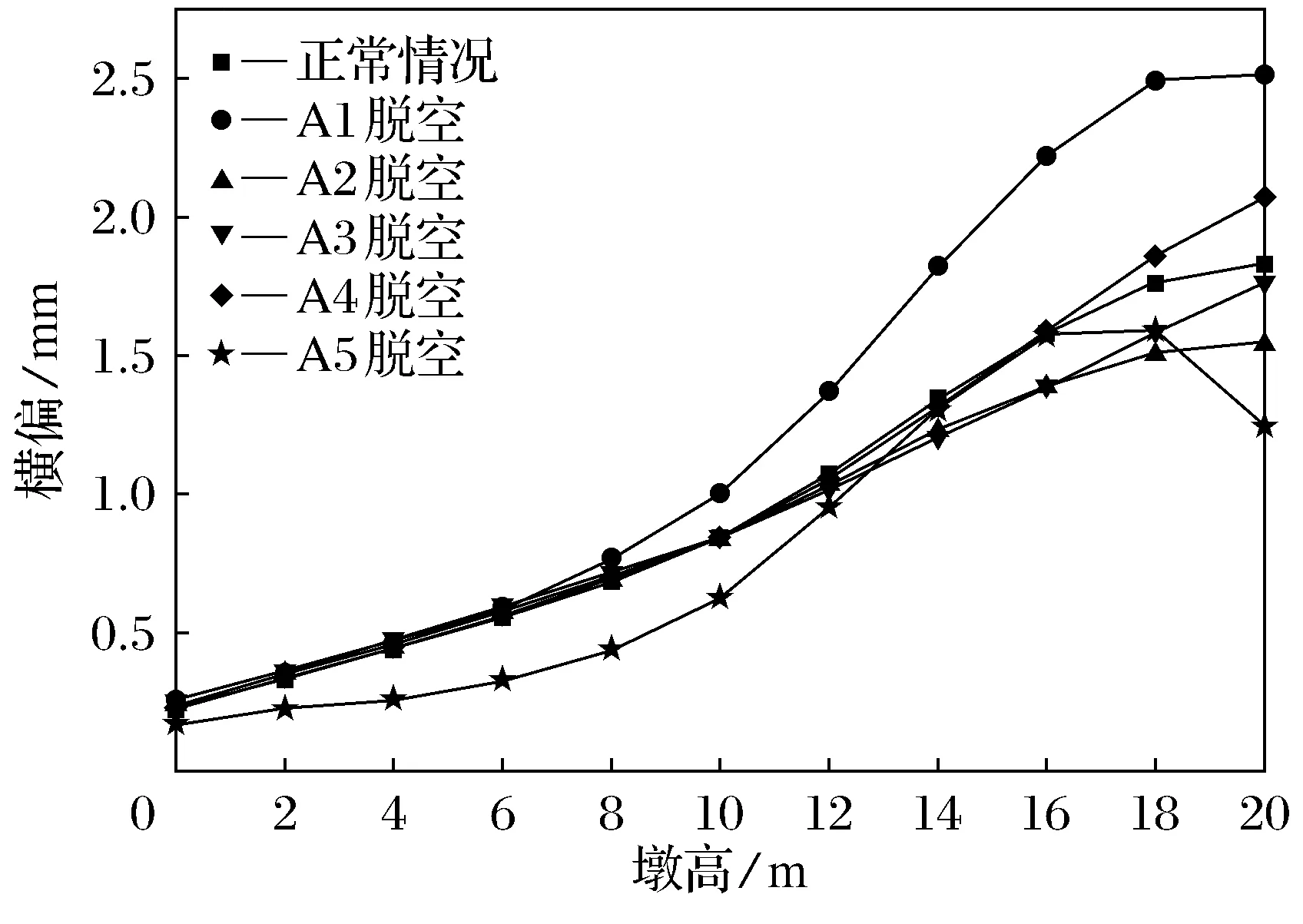
图27 A排桥墩内墩身横向偏位图(lb=30 m)Fig.27 Inner pier transverse deviation of piers of row A(lb=30 m)

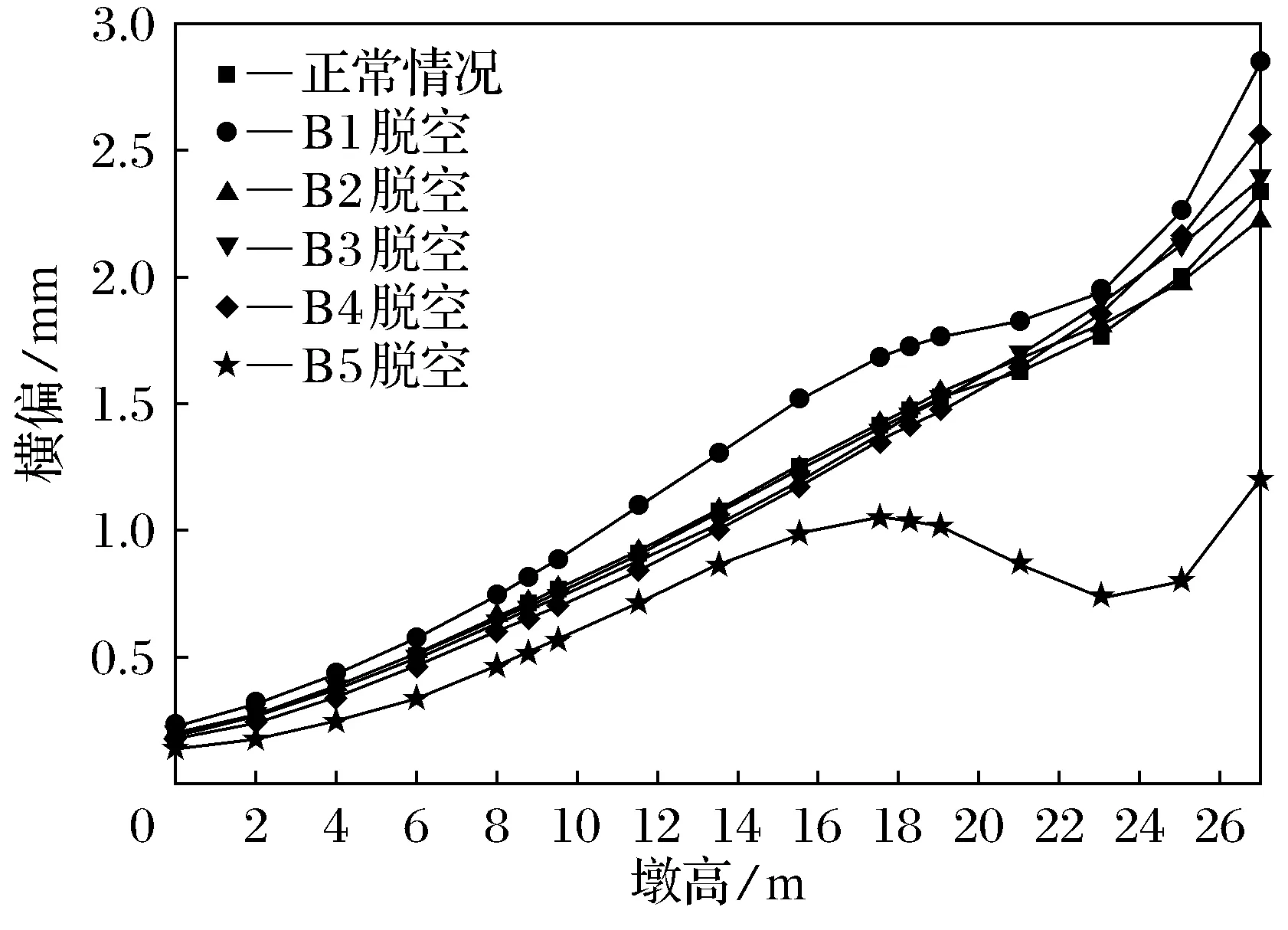
图28 B排桥墩外墩身横向偏位图(lb=30 m)Fig.28 External pier transverse deviation of piers of row B(lb=30 m)

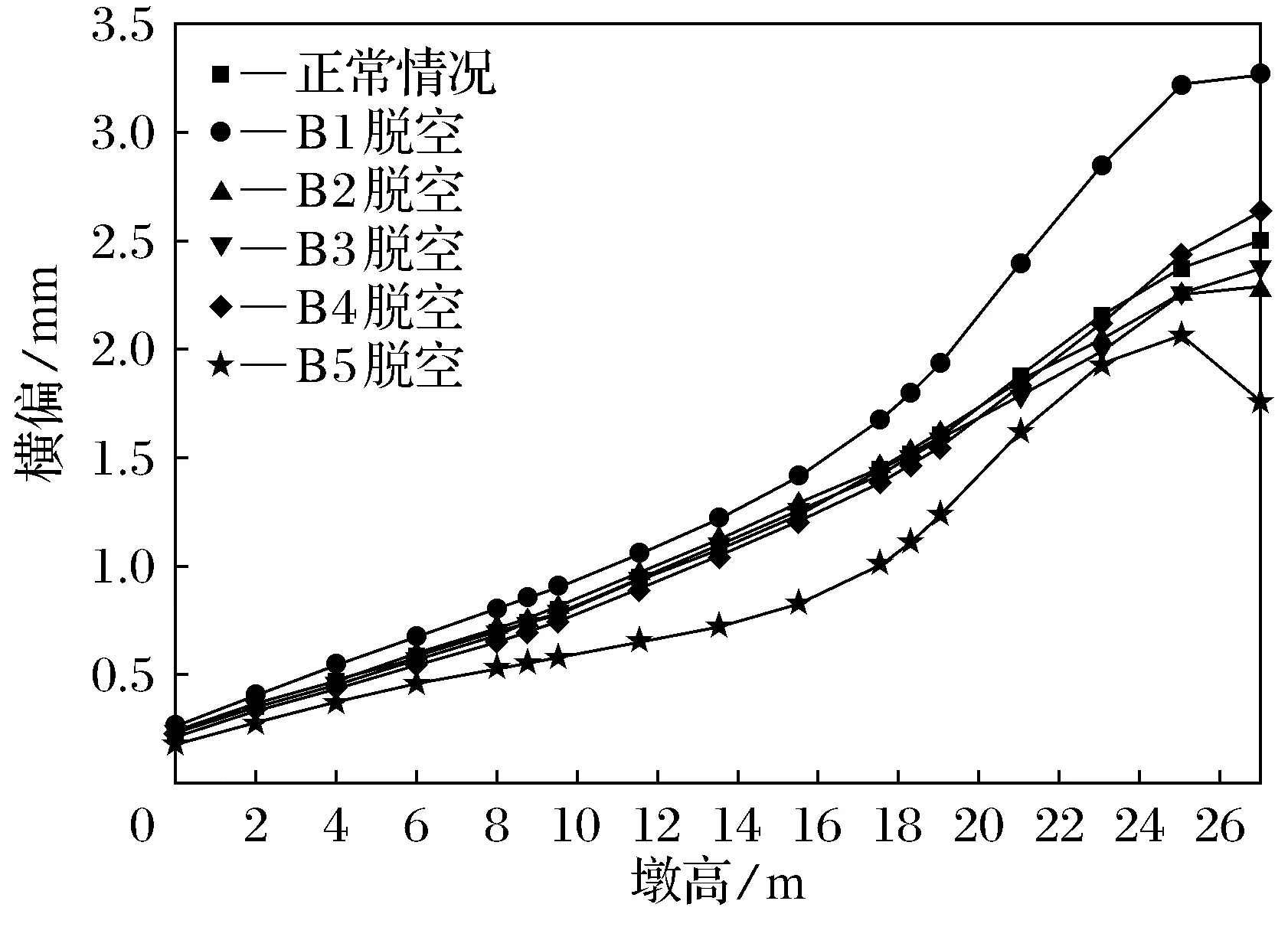
图29 B排桥墩内墩身横向偏位图(lb=30 m)Fig.29 Inner pier transverse deviation of piers of row B(lb=30 m)

6 结 论

支座脱空后,支反力会重新分布,与正常情况相比,墩顶载荷会有很大的不同,尤其是脱空处的相邻支座反力增加得更大,桥墩的受力性能因此发生变化,影响结构安全和使用性能.本文结合桩-土相互作用,分析了不同位置支座脱空后盖梁和墩身截面弯矩变化和墩身横向偏位变化规律.经过分析得出以下结论.

(1) 边梁支座脱空对盖梁截面弯矩的影响范围最大,且均大于正常值,此时跨中截面的受力最不利,弯矩值均超出正常值很多,容易造成拉应力超标,导致结构开裂破坏.因此,应该在设计和施工过程中采取相应的措施,避免边梁出现支座脱空现象.

(2) 边梁支座脱空对横系梁上侧墩身弯矩的影响最显著,其余支座脱空后的弯矩值大小均接近甚至小于正常值.内、外墩身弯矩最大值出现在墩身顶面,其中边梁支座脱空时其弯矩值最大且均超出正常值很多.

(3) 由于横系梁的设置降低了桥墩高细比,增加了桥墩刚度,提高了桥墩稳定性.因此,支座脱空后桥墩两侧墩身的横向偏位程度均较小.