基于忆阻器的Lü超混沌系统的分析与实现

方 淼, 谢苗苗, 方 帆

(1. 安徽大学江淮学院 理工部, 安徽 合肥 230039; 2. 巢湖学院 教务处, 安徽 巢湖 238000)

自1963年著名的气象学家Lorenz在研究大气湍流现象时提出经典Lorenz系统[1]以来,各种混沌系统被相继提出,对混沌现象和理论的研究成为研究热点和重点.随着对混沌科学研究的进一步发展,混沌研究从对混沌现象的揭示和刻画转向理论研究和实际应用相结合[2],对混沌生成模型的探究及混沌信号的处理和应用研究已成为重要的研究课题.Lü系统[3]是Lorenz系统族中结构最简单的混沌系统,但具有丰富的动力学行为,其随着系统参数的改变会在Lorenz系统和Chen系统之间转换,是混沌理论与应用研究的经典三维混沌模型.为了更好地满足保密通信和信息隐藏的需要,人们提出构造超混沌电路系统来提高系统的复杂性,超混沌系统会呈现更为复杂的结构和动力学行为.目前往往通过给三维连续混沌系统上加载反馈控制器的方式构建超混沌系统.反馈控制器分为线性和非线性[4],非线性的反馈项将进一步增加系统的复杂性和不可预测性,更适用于构建超混沌系统.

忆阻器[5]是蔡少棠教授1971年根据电路的完备性提出的描述电荷和磁通关系的非线性元件,由Strukov等[6]在物理上成功实现.忆阻器具有电阻、电感、电容3种基本元件不能复制的记忆特性,能够记忆流经它的电荷量,通过控制电流可改变其阻值,是一种具有记忆特性的非线性元件.利用忆阻器的非线性和记忆特性,将其作为超混沌系统的反馈项,可产生复杂的非线性动力学现象,为超混沌电路的设计提供了全新的发展空间.

目前构建超混沌系统主要有以下2种实现方法.

(1) 采用忆阻器作为典型混沌系统的反馈项构建超混沌电路系统.包伯成[7]等人通过在三维Bao系统中加入1个新的状态变量,实现了四维超混沌系统;阮静雅等人[8]利用忆阻器作为正反馈项构建了Lorenz超混沌系统,设计实现了系统的模拟等效电路.

(2) 通过给振荡电路增加非线性元件或进行非线性耦合实现超混沌.Li等[9]将2个文氏电路进行非线性耦合获得文氏超混沌电路,但这些忆阻电路结构过于复杂,不利于进行电路实现.

为此,如何构建一种电路结构更简单,动力学行为更丰富的电路系统,以满足保密通信和信息隐藏等领域的要求,也是超混沌系统的研究思路.

本文采用3次型磁控忆阻器作为Lü系统的非线性反馈项,构成1个简单的四维忆阻系统,获得了超混沌信号,同时对该超混沌系统的特性进行了分析,采用相图、Lyapunov指数谱及分岔图等基本动力学分析方法对系统的非线性动力学行为进行了研究,分析了系统参数的变化对系统动力学特性的影响,最后设计实现了该超混沌系统的模拟等效电路,并利用PSPICE软件进行仿真,实验仿真的结果和数值仿真的结果一致,对超混沌电路的工程应用具有一定的理论和实际意义.

1 基于Lü系统的超混沌忆阻系统模型

1.1 Lü系统的数学模型和电路实现

Lü系统是介于Lorenz系统和Chen系统之间的转换系统,是Lorenz系统族中结构最为简单的系统,其数学模型[3]可用1个连续自治耗散三维常微分方程组描述为

(1)

式中:x,y,z为系统的状态变量;a、b、c为实参数.

固定参数a=36,b=3,当参数c∈(18,22)时,系统处于混沌状态,能产生不同于Lorenz系统和Chen系统的新的混沌吸引子,如图1所示.采用模拟集成运放和乘法器可实现该混沌系统(1),如图2所示.

图1混沌吸引子
Fig.1 The chaotic attractor

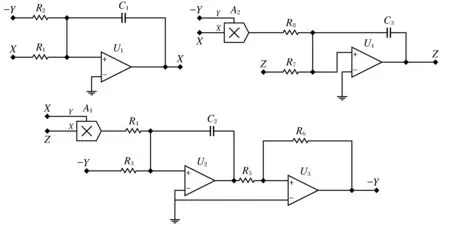
图2 Lü系统模拟电路图Fig.2 Analog circuit of the Lü system

为提高系统的复杂性和不可预测性,在该系统中增加1个非线性反馈项,构建新的超混沌电路系统.忆阻器作为具有记忆特性的非线性电阻器,适于作为系统的非线性反馈项构建超混沌系统.本系统采用Bao提出的磁控忆阻器作为系统的反馈项,该磁控忆阻器由1条光滑单调上升的3次非线性特性曲线描述[10],即

q(φ)=αφ+Bφ3.

(2)

式中:q为电荷;φ为磁通;α>0,β>0为实参数.

该曲线的斜率,即其电荷随磁链的变化率,称为忆阻器的忆导,为

(3)

式中,α>0,β>0,忆导是随内部状态变量φ变化的函数.设给忆阻器两端施加电压V,则流过忆阻器的电流为I,可得

1.2 Lü超混沌系统的数学模型

令忆阻器的控制电压V=x+y,w=φ,则有

I=W(w)V=(α+3βw2)(x+y).

(6)

将忆阻器的电流I作为反馈项引入Lü系统,根据基尔霍夫定律可得基于忆阻器反馈的Lü系统的系统方程:

(7)

为了获得无量纲方程,令w=φ,选择参数a=36,b=3,c=29,α=0.2,β=0.04,并设置初始条件为(10 10 10 0),系统(7)产生双涡卷超混沌吸引子,如图3所示.图4a、图4b分别给出了超混沌吸引子在x-y和y-w平面上的投影.

由图3、图4可见, 由于忆阻器的忆导值受忆阻器内部控制变量的影响, 当将忆阻器引入Lü系统时, 引入了1个新的状态变量, 该系统所产生的混沌吸引子的拓扑结构远比三维的Lü系统复杂. 通过寻找合适的Poincaré截面, 能将系统随时间连续变化运动转化为Poincaré截面上的离散映射, 该映射降低了系统的维数, 但仍能保持原有动力学系统的拓扑性质[8], 能更好地刻画出该忆阻电路的混沌特性. 图5a、图5b分别给出了x=0和z=30截面上的Poincaré映射, 显然基于忆阻器的并联混沌电路的Poincaré映射上存在无穷多个密集点, 吸引子的轮廓清晰可见, 表现出分形的几何特征, 进一步说明该系统是超混沌的.

图3超混沌系统吸引子
Fig.3 The chaotic attractor of hyper-chaotic system

图4 超混沌系统相轨图Fig.4 The phase portrait of hyper-chaotic system

图5 系统(7)的Poincaré映射Fig.5 Poincaré section of system (7)

利用Jacobi方法计算该系统的Lyapunov指数得:LE1=9.73;LE2=0.04;LE3=-0.81;LE4=-10.04.系统包含2个正的Lyapunov指数,且满足所有Lyapunov指数之和小于零,表明该系统处于超混沌状态.从吸引子的相轨图和Lyapunov指数可以判断出忆阻系统是超混沌振荡的.

2 动力学特性分析

2.1 对称性

由于系统(7)满足(x,y,z,w)～(-x,-y,z,-w)的变化下保持不变,因此该系统关于z轴对称,这种对称关系对系统所有的参数均成立.

2.2 平衡点稳定性分析

E={(x,y,z,w|x=y=z=0,w=m)},

其中m为实常数,即w坐标上所有的点均为平衡点,系统存在无穷的平衡点集.在平衡点处对系统(7)进行线性化,可得Jacobi矩阵JE为

选取数值仿真时所采用的参数,且取平衡点m=0,可求得系统的特征值λ1=0,λ2=-3,λ3=-18.06,λ4=28.9,即系统的平衡点是1个不稳定的结点,并且当|m|<31.04时,系统平衡点均为不稳定的结点,否则平衡点集是稳定的.

2.3 参数改变对系统的影响

由于系统(7)具有无限平衡点集,包含无限的稳定和不稳定的平衡点,因此该系统具有丰富的非线性动力学行为.为了进一步研究系统的动力学特性,通过改变电路参数对Lyapunov指数谱和分岔图进行分析.随着系统参数的改变,系统平衡点的稳定性也将随着改变,从而使系统处于不同的状态.在初始条件(10 10 10 0)下,固定电路参数a=36,c=29,α=0.2,β=0.04,选择b为可变电路参数.当b∈[1,15]时,Lyapunov指数谱和状态变量x的分岔图如图6所示.

图6 系数随参数b变化的Lyapunov指数谱和分岔图Fig.6 The Lyapunov exponential spectrum and bifurcation diagram of the system change with b

由图6可见,系统的Lyapunov指数谱和分岔图的稳定和不稳定区间基本一致.当02.4时,Lyapunov指数形式为(+,+,-,-),系统失稳,进入超混沌状态.当b>6时,Lyapunov指数基本保持恒定,系统处于恒定混沌状态,说明此时系统不因参数b的扰动或微小变化而导致状态发生变化,其结构稳定,具有强鲁棒性[11],适合作为随机信号源,产生性能良好的伪随机序列.

同样,参数c也会影响系统状态,在相同的初始条件下,固定其他电路参数,选择c为可变电路参数.当c在[10,40]范围内变化时,系统的Lyapunov指数谱和状态变量x的分岔图如图7所示.

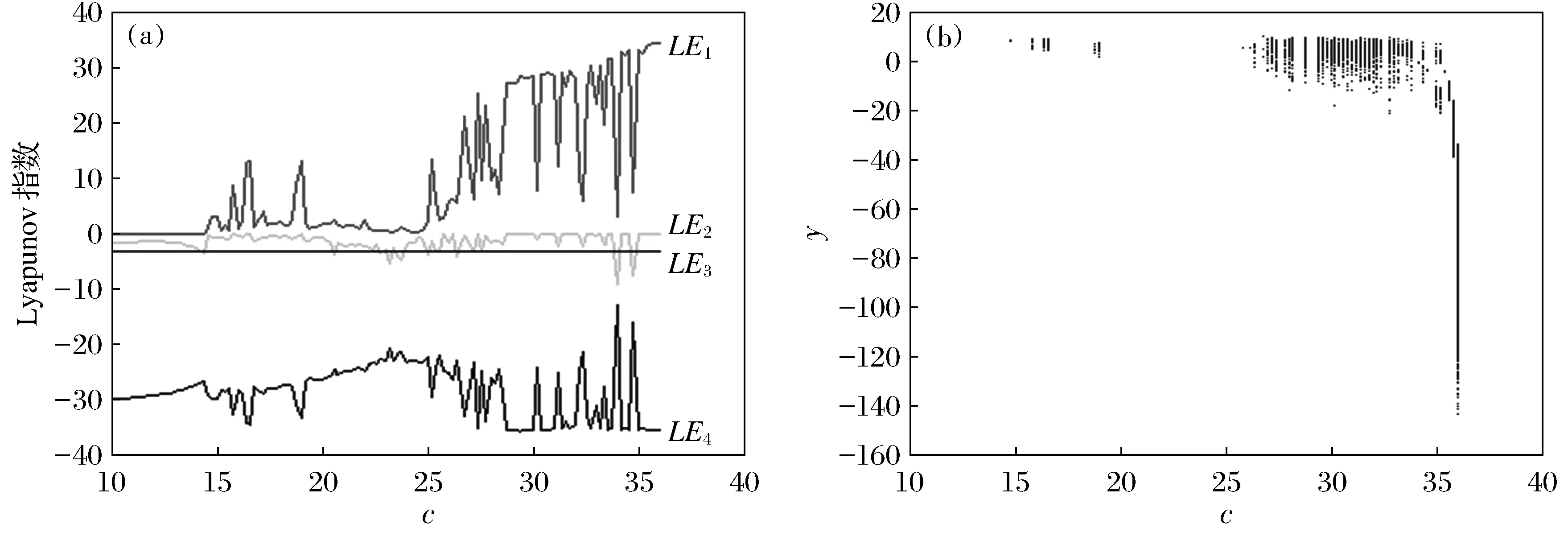
图7 系数随参数c变化的Lyapunov指数谱和分岔图Fig.7 Lyapunov exponential spectrum and bifurcation diagram of the system change with c

由图7可见,Lyapunov指数谱和分岔图所表现的运动轨迹一致.随着参数c的增加,系统从周期态进入混沌和超混沌状态,其中出现了若干个周期窗口,经历了复杂的非线性变化过程.并且从图中可以看出,系统在c=[28,35]的很长一段区域内均处于超混沌状态,在保密通信和信息隐藏中具有一定的应用价值.

3 等效电路实现

为进一步验证系统的超混沌行为,采用电阻、电容、运放和乘法器构建出跟随器,积分器和电流转换器来等效实现忆阻器,如图8所示.

图8 忆阻器的等效电路原理图Fig.8 The equivalent schematic circuit diagram of the memristor

将该忆阻器作为反馈项引入Lü系统,实现系统(7)的运算,电路中采用AD712运放,乘法器为AD633,由于模拟乘法器的容许电压范围为±10 V,运放的容许电压范围为±15 V,为确保电路变量工作在合适的动态范围内,在不改变系统性能的条件下对系统状态变量做合适的线性变换,即

变换后系统(7)对应的方程为

(8)

设计的系统实验仿真电路如图9所示.

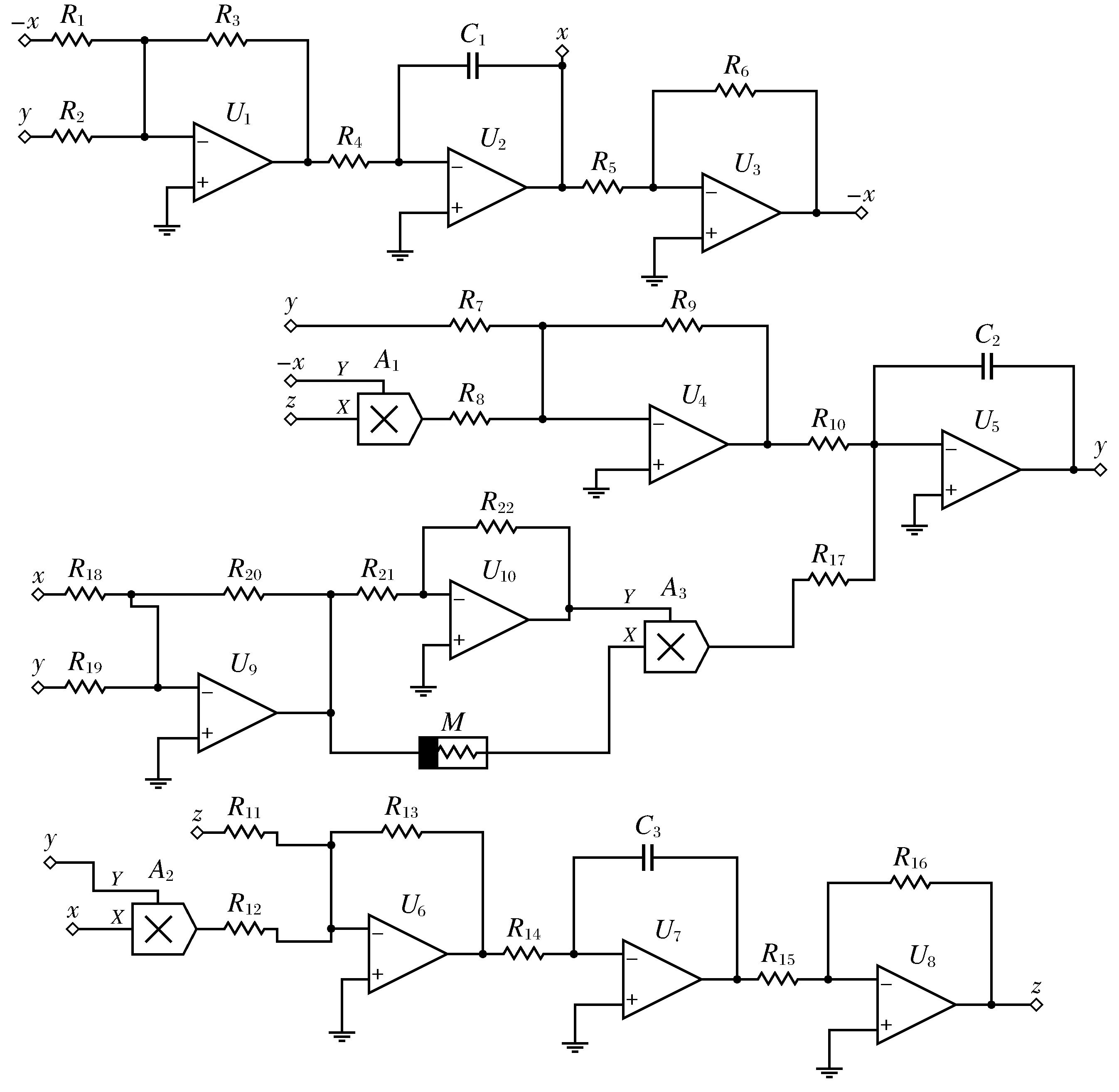
图9 超混沌系统电路图Fig.9 The circuit diagram of the hyper-chaotic system

采用PSPICE软件对上述电路进行仿真验证,将式(7)和式(8)对应的系数进行比较,并合理地设置,相应的元件值分别为:Ci(i=1,2,3,4)=1 μF;Ri(i=1,2,7,18,19,20)=1 kΩ;R3=360 Ω;R8=2.9 kΩ;R9=290 Ω;R12=3 kΩ;R13=300 Ω;R17=100 kΩ;Ri(j=4,5,6,10,11,14,15,16,21,22)=10 kΩ.得到仿真结果如图10所示,电路仿真结果和数值仿真结果基本一致,验证了该超混沌电路的正确性.

4 结 论

本文基于Lü系统设计了一种新的超混沌系统,该系统具有无限的平衡点集,并且由于磁控忆阻器的非线性反馈,使得系统包含丰富的动力学行为. 数值仿真结果表明, 该系统能够产生超混沌吸引子, 当参数增加到一定值时,

出现了恒定

图10 超混沌系统电路仿真图Fig.10 The circuit simulation diagram of the hyper-chaotic system

Lyapunov指数谱,说明该超混沌系统不仅结构简单、稳定,且具有很好的鲁棒性.为了进一步验证系统的动力学行为,采用通用的运算放大器和模拟乘法器实现了系统的模拟等效电路,并对该等效电路通过PSPICE软件进行了电路仿真,仿真结果与数值仿真及理论仿真结果一致,验证了电路的有效性和可实现性,其复杂的超混沌特性和恒Lyapunov指数谱现象使该系统在混沌保密通信中具备潜在的应用价值.