高压实膨润土膨胀力预测研究
陈永贵,蒯 琪,叶为民1,,崔玉军
(1. 同济大学 岩土及地下工程教育部重点实验室,上海 200092;2. 同济大学 土木工程学院,上海 200092; 3. 法国国立路桥大学,巴黎 77455)
随着核电技术发展,核能已成为世界三大能源供应之一,由此产生了大量的高放射性核废物(以下简称“高放废物”).据估算,到2020年,我国累积重金属(heavy metal, HM)乏燃料将达到约10 000 t ,此后每增加一座百万千瓦级的核电站,每年将产生22 t HM乏燃料[1].高放废物的处置已成为困扰核工业全面发展的关键.国际上主要采用多重屏障处置库对高放废物进行深地质埋藏,即将高放废物封存在距地表500~1 000 m深的稳定岩体内,设置人为屏障来阻止核素泄漏进入生物圈.通常,多重屏障处置库由固化体、高放废物金属罐、作为人工屏障的缓冲回填材料以及天然屏障地质体等部分组成.在深地质处置库的工程屏障体系中,缓冲回填材料在减缓地下水渗流、阻止核素迁移、维持废物金属罐稳定及传递核素衰变热等方面起着至关重要的作用[2].
早在上世纪80年代,瑞典科学家Pusch经过一系列研究认为,以蒙脱石为主要成分的高压实膨润土具备上述多重屏障功能,是最适合的人工屏障缓冲回填材料[3].随后,法国、美国、比利时等国科学家通过大量试验研究,都选择膨润土作为处置库的缓冲回填材料[4-7].我国的高放废物处置库建设始于上世纪80年代,目前已选定内蒙古高庙子(GMZ)膨润土作为首选缓冲回填材料,并将处置库地下实验场建设列入“十三五”期间100项重点项目计划.
高放废物处置库缓冲回填材料是置于高放废物金属罐与围岩之间的材料,也是高放废物处置库最后一道人工屏障材料.它的主要作用是:充填废物容器与围岩间的空隙和近场岩石中的裂隙或孔隙,将容器固定在一定的位置,缓冲围岩压力对废物金属罐的影响,阻止地下水进入废物包装容器,改变地下水的化学成分,调节地下水的pH值,阻滞核素迁移,同时也对辐射热起着重要的导体作用[8].由此可见,膨胀特性对高压实膨润土工程屏障功能的发挥至关重要.
针对缓冲材料膨胀特性,各国学者将膨胀力和膨胀变形量作为主要评价指标,开展了大量的室内试验、理论分析及数值模拟研究工作.近年来,许多学者从工程实际出发,基于高压实膨润土的水化膨胀机理,建立了缓冲回填材料膨胀力的计算模型,以期为工程屏障系统设计提供理论支撑.本文基于已有研究成果,揭示了高压实膨润土的水化膨胀机理,阐述了不同水化机理的膨胀行为预测模型,并对不同模型计算结果进行了分析,以期为高放废物处置库建设中缓冲回填材料的选择、工程屏障系统的设计以及处置库运营的安全评估提供依据.
1 膨胀机理
1.1 膨润土水化过程
蒙脱石是膨润土的主要矿物成分,其质量分数高达70%~90%,如作为缓冲回填材料的MX-80膨润土中蒙脱石质量分数为65%~82%,FEBEX膨润土中蒙脱石质量分数为92%,我国GMZ膨润土中蒙脱石质量分数为75.4%.蒙脱石结构是由两个硅氧四面体夹一层铝氧八面体组成的2∶1型晶体结构[10].处置库建成后,高压实膨润土从围岩中吸收水分,使蒙脱石水化膨胀,从而封闭施工缝隙,维持围岩稳定.
实际上,膨润土孔隙包括了晶层间孔隙、集合体内孔隙和集合体间孔隙[10],不同水化阶段引起的微观结构的变化决定着相应的膨胀力性能.从微观角度分析,膨润土的水化过程分为3个阶段(见图1):第Ⅰ阶段,晶层间孔隙被水充填,层叠体间孔隙保持干燥;第Ⅱ阶段,层叠体吸水膨胀并充填集合体内的孔隙,而集合体本身的膨胀并不明显;第Ⅲ阶段,厚层叠体继续膨胀并裂开成薄层叠体,甚至为单层晶层,导致集合体膨胀.其中,第Ⅰ阶段的膨胀是由存在于蒙脱石单元层(TOT)之间的可交换阳离子(K+、Na+、Ca2+和Mg2+)的水化作用引起的(阳离子与水发生化合反应,在其周围形成一定的水分子层),称之为晶层膨胀.后两个阶段是由于层叠体间扩散双电层(diffusion double-layer, DDL)膨胀引起的,称之为双电层膨胀.因此,晶层膨胀和扩散双电层膨胀是膨润土膨胀的两种主要机制[11].

图1 膨润土水化膨胀机理Fig.1 Swelling mechanism of compacted bentonite
1.2 晶层膨胀
晶层膨胀是由于蒙脱石矿物晶体单元层中可交换阳离子发生水化作用引起的.无水状态下,可交换阳离子在晶层表面或晶格边缘,晶层间排列紧密,间距约为0.95~1.00 nm.土颗粒遇水后,晶层表面吸附势能大于晶层之间的吸引能,水分子进入晶层之间,导致层间阳离子与水分子结合并有序排列在晶层表面上,使得晶层间距扩大,产生晶层膨胀[12].
晶层膨胀过程主要受可交换阳离子种类和土体含水率影响.钠基膨润土完全饱和时,层间有4层水分子层,而钙基膨润土最多含有3层水分子层.因此,钠基膨润土的膨胀能力大于钙基膨润土,这已被大量试验成果所证实[13].膨润土含水率不同时,晶层间水分子层数不同,对应的晶层间距亦不相同,1、2、3、4层水分子对应的晶层间距分别为0.96、1.26、1.56、1.86 nm.但是,对于含有多层晶层的层叠体来说,实际水化过程中晶层间距与含水量的变化并不同步,存在明显滞后性[9].水化初期,晶层膨胀将导致土颗粒中层叠体变薄.Saiyouri等[14]的研究表明,高压实MX-80膨润土和FoCa-7膨润土的层叠体数量可能会从350和100层下降到10层,这为后续的扩散双电层膨胀提供了足够空间.
通常,0~4层水分子有序插层进入晶层之间的晶层膨胀过程,被认为是库仑力和范德华力与黏土表面负电荷斥力之间的相互作用[15].基于此,众多学者[10,13-16]试图开发晶层膨胀的宏观计算模型.Norrish[16]提出了两种不同方程来计算层间阳离子和带负电荷表面之间的静电引力,但无法测得阳离子水化斥力的能量,从而计算也不够准确.Olphen[17]和Kittrick[18]提出的晶层膨胀模型因需要特定的矿物热力学性能参数,也缺乏普遍适用性.
1.3 扩散双电层膨胀
膨润土中蒙脱石由于同晶置换作用而带有负电荷,对于周围的阳离子和极性水分子具有极强的吸附作用.因此,土颗粒表面吸附的阳离子浓度远高于附近溶液的离子浓度.膨润土遇水后,孔隙流体和黏土-矿物表面之间存在一定的渗透势.通常情况下,阳离子会从浓度较高处扩散到浓度较低处,以便均匀地分布在溶液中.在膨润土中,因为离子是由土颗粒所带电荷控制的,水从低离子浓度(高浓度的水)运移到高离子浓度(低浓度的水)区域,使得晶层之间或层叠体之间间距增大.带电的膨润土颗粒表面及相邻的分布电荷和水分子层一起被称为扩散双电层[19-20],见图2.由于扩散双电层形成过程受渗透势控制,此过程又称渗透膨胀.
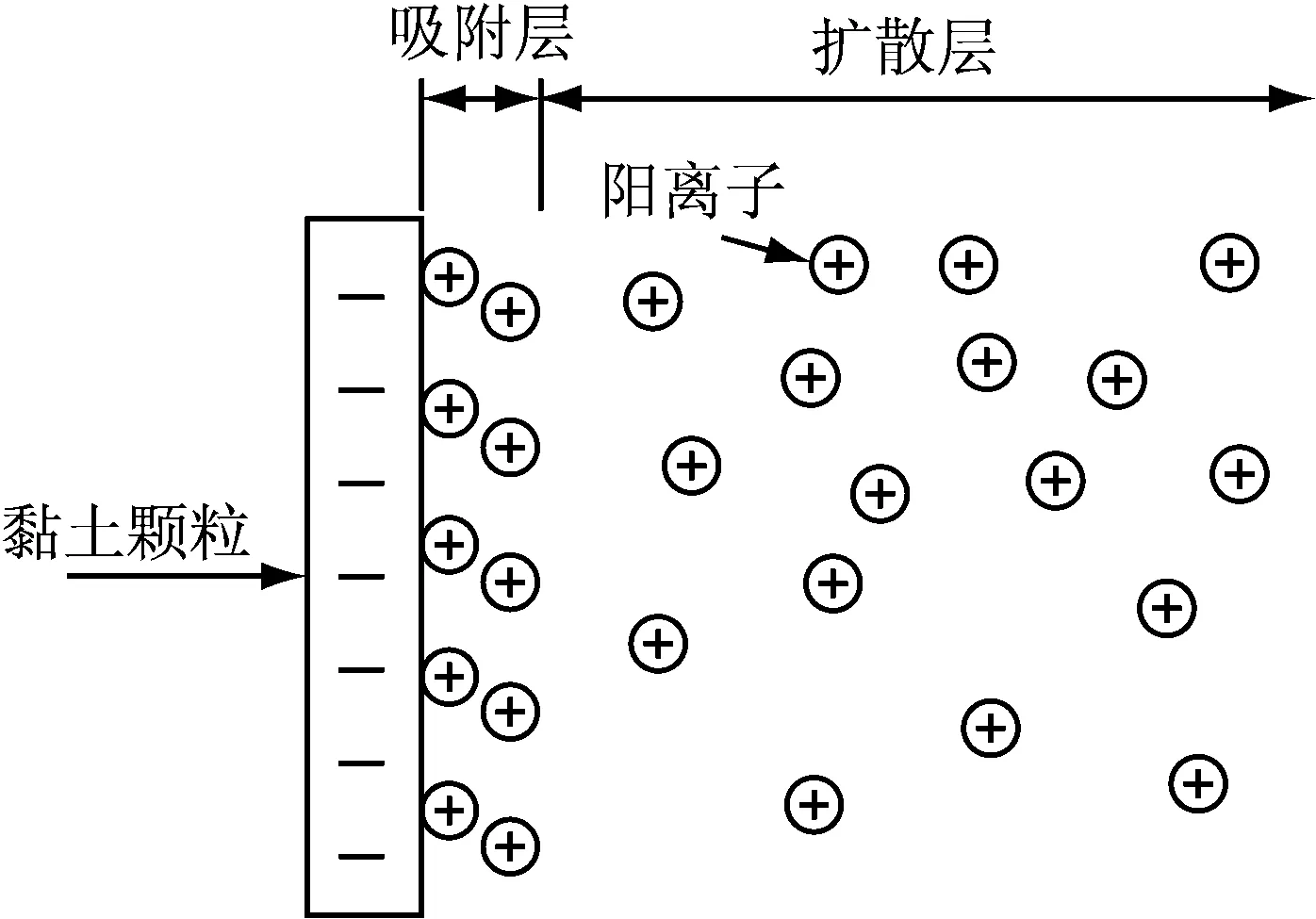
图2 膨润土扩散双电层结构Fig.2 Structure of diffused double layer
当可交换阳离子结合的水分子层厚度达到最大(3~4个水分子层厚)后,阳离子水化作用减弱,晶体膨胀结束,扩散双电层膨胀成为控制膨胀过程的主要机制[21].根据Gouy-Chapman扩散双电层理论[21],两个相邻平行晶层中间平面处的离子浓度是影响两个晶层之间扩散双电层的重要因素[17].因此,对于确定的两个相邻平行晶层之间的距离,可以通过中心平面的离子浓度来确定渗透压.同样,对于任何给定的渗透压和在两个晶层之间中心平面的离子浓度,均可以确定晶层间距.Bolt等学者[19-20,22]证明了上述理论应用于饱和黏土具有很好的一致性.Komine[23]基于这一理论,建立新的方程,计算高压实膨润土的膨胀应变和膨胀力;Sridharan[27]进一步验证了新方程应用于确定具有较大扩散双层厚度(如浆状黏土)土体中平面电位函数的有效性.因为,对于含水量较高但仍不饱和的压实黏土,初始阶段的膨胀是由相邻黏土颗粒之间产生的排斥力所引起,这种排斥力发生在蒙脱石层叠体之间,受渗透势驱动,可以由扩散双层理论确定[24-25].而对于高压实膨润土或含水量较低的干压实黏土,初始阶段的膨胀是由土颗粒表面附近的离子水合力引起,即为晶层膨胀而非扩散双电层引起的膨胀,此种情况并不适用于扩散双电层理论.因此,Komine[23]建立的新方程的适用条件具有一定局限性.
Gens等学者[26-28]进一步论证了基于扩散双层理论的计算结果与试验数据之间的差异性.这主要是受以下因素的影响:①土体中存在发育不良或部分发展的扩散双电层;②土颗粒成分差异,土体中存在多种矿物成分;③紧密颗粒处的表面水合力;④水的张力直接机械效应;⑤层叠体的不均匀尺寸;⑥电吸引力的存在;⑦多价阳离子的存在;⑧在施加高压缩应力的情况下离子尺寸;⑨阴离子吸附;⑩粒径;排斥扩散双层水.这些因素与黏土的初始应力状态息息相关,其中某个或几个因素组合就可能导致理论计算与试验结果之间的差异.
Bolt[20]认为,即使对于浆状黏土,黏土的实际微观结构也与平行板概念略有偏离.
为了克服上述Gouy-Chapman扩散双电层理论计算的不足,许多学者试图提出不同方法来确定膨润土的膨胀力.Yong[29]提出了DLVO理论,该模型在黏土-水相互作用中考虑了静电双电层斥力和范德华力,但仍然无法解释钙基蒙脱石和高压实黏土的试验结果[25,28-30].
2 膨胀行为预测经典模型
由于晶层膨胀过程涉及复杂的物理化学过程,影响因素过多,同时会产生相互作用,因此目前有关晶层膨胀的模型研究成果较少.而有关扩散双电层模型的研究成果较为丰富,其源于物理化学领域,模型研究相对成熟,近年来常被应用于研究非饱和土.如何结合膨润土特有性质进一步完善该模型,准确预测缓冲回填材料在处置库运营期间膨胀性能的变化将是重要的研究方向.
2.1 Laird模型
Laird是目前唯一一位对晶层膨胀进行全面定量分析的学者[11].从能量角度分析,将晶层间的排斥能分为阳离子水合能、晶层表面水合产生的排斥能以及Born斥能;吸引能则包括阳离子对两侧表面的吸引能和范德华吸引能.
阳离子水合能Gh i可表达为
(1)
式中:ρ为电荷密度;v为膨润土所含离子的化合价;q为单位电荷量,q=1.6×10-19C;ε0为真空介电常数,ε0=8.854 2×10-12F·m-1;εr为体相相对介电常数;εb为晶层之间相对介电常数,εb=78.18 F·m-1;ri为离子i的有效半径.
晶层表面水合能是由于晶层内部所带负电荷的静电场引起的,Laird借鉴阳离子水合能的表达方法,将晶层厚度一半等效于离子半径,则晶层的两个表面或层间的两个侧面的总水合能Ghs为
(2)
式中:rs为晶层厚度的一半,rs=4.7×10-10m.
Born斥能Gb是为防止两个原子的电子云占据同一个空间的势能,可表示为
(3)
式中:L为常数,L=1.45×10-124J·m10;d为晶层间距的一半.
阳离子对两侧表面的吸引能Ga i为
(4)
式中:fi为常数,fi=0.72.
范德华吸引能Gv为
(5)
式中:λ为晶层厚度;H为Hamaker常数.
综上,对外显现的膨胀势能Gs则为所有排斥能与所有吸引能之间的差值,即
Gs=Gh i+Ghs+Gb-Ga i-Gv
(6)
2.2 Helmholtz模型
Helmholtz[31]第一个提出了扩散双电子层理论.带有负电荷的晶层能吸附周围液体中的阳离子,正负电荷整齐地排列于界面两侧,电荷分布情况如同平行板电容器,其间距为阳离子半径,如图3所示.平板上的电势由Poisson-Boltzmann表示
(7)
式中:φ为电势能;x为与平板的距离.由于该模型将带电离子视作质点排列在平板上,不考虑离子大小,所以
(8)
这表明平板周围电势为线性分布.该模型过于简单,不能解释带电质点的表面电势与质点运动时固液两相发生相对移动时所产生的电势差,也无法反映出电势与电解质中离子浓度的关系.
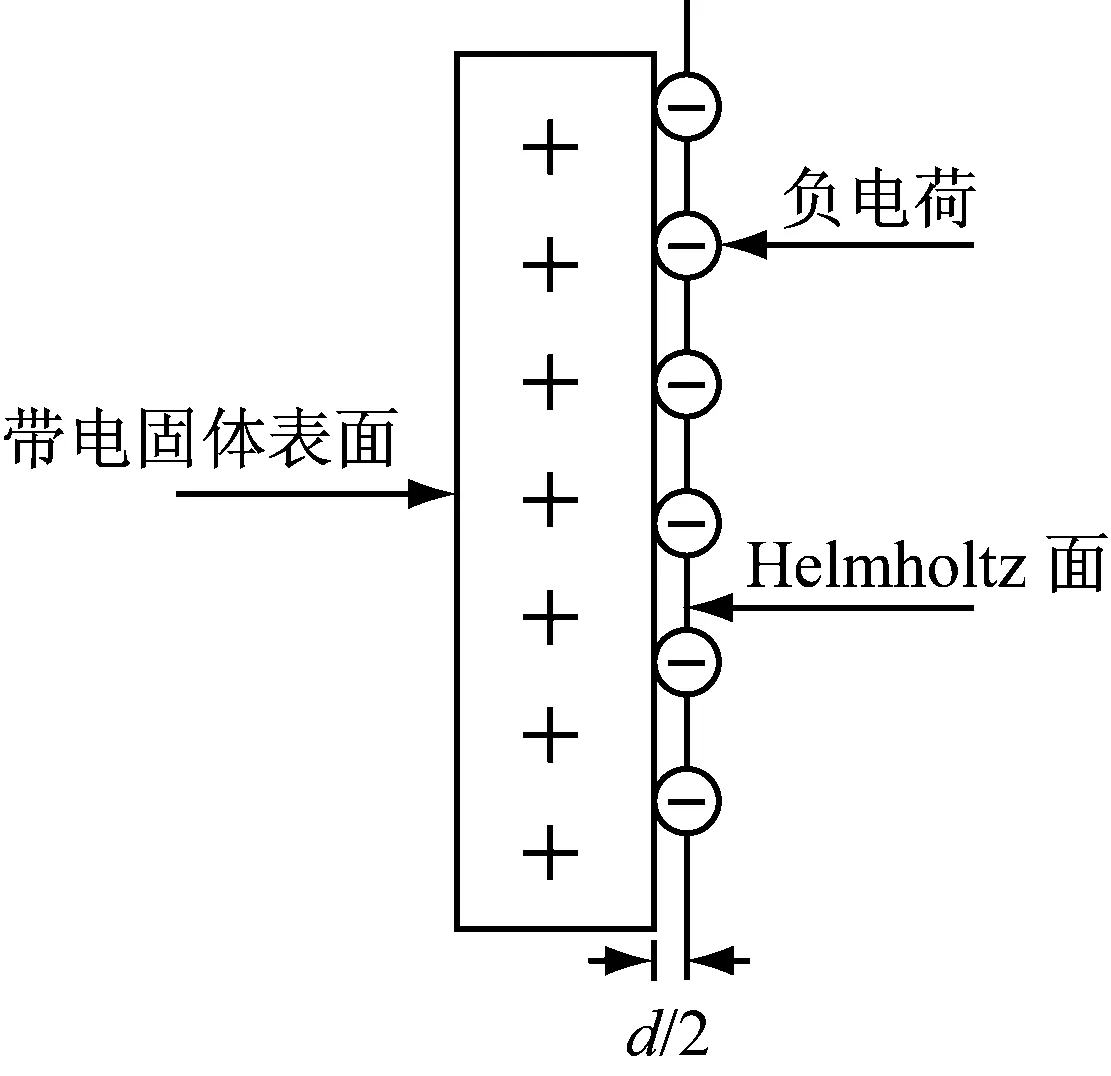
图3 Helmholtz 模型Fig.3 Helmholtz model
2.3 Gouy-Chapman模型
Gouy[32]和Chapman[33]分别提出了双电层模型,如图4所示.考虑了连续介质中存在的反离子呈扩散状态分布在溶液中,而非整齐地排列在一个平面上.
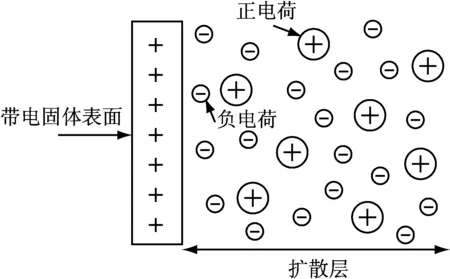
图4 Gouy-Chapman模型Fig.4 Gouy-Chapman model
Gouy-Chapman模型的基本假设有:① 电荷均匀分布在无限大的平面上;② 不考虑带电电荷的大小,其分布服从Boltzmann 定律;③ 溶液的介电常数处处相同.
连续介质中离子浓度服从Boltzmann分布
(9)
式中:ni 0为溶液中i离子的浓度;k为Boltzmann常数,k=1.38×10-23J·K-1;T为绝对温度,取298 K;vi为离子i的化合价.
电荷密度则为
(10)
根据Poisson-Boltzmann方程,得
(11)
由于
(12)
那么
(13)
存在如下约束条件:
x=0,φ=φ0
所以
(14)
(15)
(16)
式中:1/K为扩散双电层厚度.
Verwey[30]在此基础上,将两个平行的带电晶层视作平板电容器,如图5所示.图中φd为距平板距离为d时的电势能.
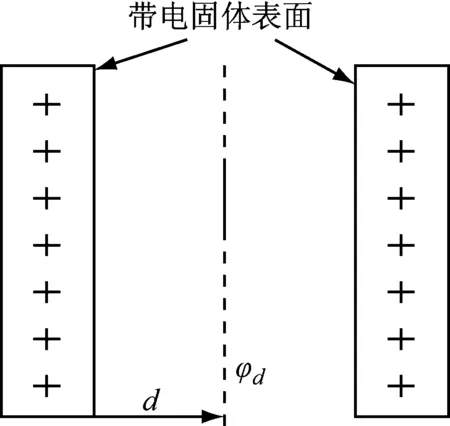
图5 修正 Gouy-Chapman模型Fig.5 Modified Gouy-Chapman model
根据平板电容器原理
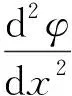
(17)
式中:Q为平板所带电荷量;n为介质中离子浓度.
约束条件为
φ=φd
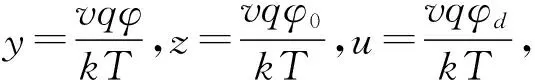
(18)

(19)
(20)
(21)
则膨胀力为
(22)
Olpehen[17]提出
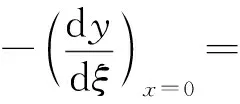
(23)
ξ=Kx
(24)
结合Bolt理论[22],得到广泛适用的DDL模型
e=GγwSd
(25)
式中:e为孔隙比;G为比重;γw为水的重度;S为比表面积.
(26)
(27)
PDDL=2nKT(coshu-1)
(28)
式(28)表明,随着1/K的增大,膨胀力PDDL值逐渐减小.
Gouy-Chapman模型假设中,扩散离子作为点电荷处理,但事实上不同离子的半径不同,因而水化作用产生的膨胀势也不同,因此并不能反映出界面附近紧密层的存在.
2.4 DLVO模型
DLVO模型是在Gouy-Chapman双电层模型的基础上,引入了范德华力,认为双电层斥力与范德华力之差即为渗透膨胀力.范德华力为
(29)
Pt=2nkT(coshu-1)-Pv
(30)
2.5 Stern模型
从上述分析出发,Stern[34]考虑了吸附离子的大小,提出了进一步的修正模型.Stern认为溶液中反离子受到范德华力牢固吸附于晶层表面,这些反离子构成Stern层,其外游离的电荷定义为外扩散层.如图6所示,晶层表面吸附电荷的半径即为Stern层厚,以离子中心面为Stern面,带有恒定电势ψδ,是扩散双电层的起始面.
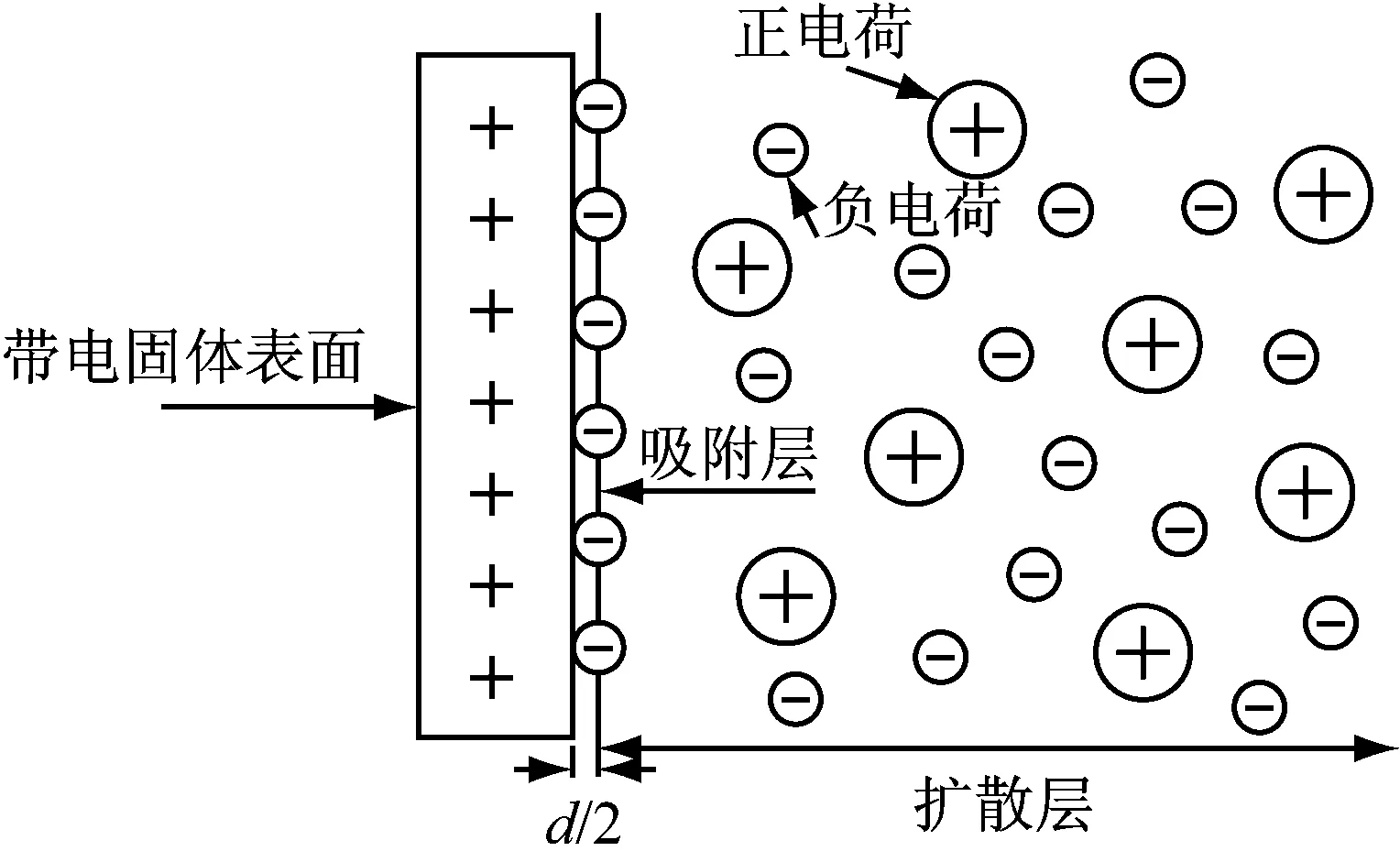
图6 Stern模型Fig.6 Stern model
(31)
式中:ψ0为晶层表面的电势;ψδ为平板中心线处的电势;Q为总电荷量,即为Stern层表面σ1与中心线处的电荷σ2之和;ε′为孔隙水介电常数;δ为Stern层厚度.
Stern层电势是由范德华力的吸附作用引起的,可用Langmuir吸附等温式描述Q1
(32)
式中:N1为每平方米吸附位点;NA为阿伏伽德罗常数;M为分子量;w为Laird模型参数,且w=0.064;φ为吸附势.
根据Gouy-Chapman模型,知
(33)
ud=vqψd/kT
(34)
zδ=vqψδ/kT
(35)
(36)
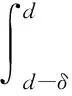
(37)
P=2nkT(coshud-1)
(38)
e=GγwSd
(39)
3 模型应用
当高压实膨润土块体放置在处置库中形成工程屏障后,膨润土将从围岩中吸收水分后不断水化,填充施工缝隙并维持围岩稳定.设计和建造高放废物处置库过程中,缓冲材料的膨胀力是基本参数,同时也是衡量膨润土膨胀性能的关键指标[35].因此,合理预测膨润土水化后的稳定膨胀力,是工程屏障设计和建造的关键.
3.1 晶层间距对膨胀力的影响
由前文分析可知,晶层间距对膨胀力的大小有重要影响.对相同干密度压实膨润土而言,恒体积条件下吸收水分越多,水化越充分,晶层间距越大,膨胀力也越大.对不同干密度压实膨润土而言,干密度越小,集合体间孔隙越大,层叠体随着吸收水分、不断水化而裂开,并充填在集合体间孔隙中,此时晶层间距增大.因此,恒体积条件下,初始干密度越小的压实膨润土,集合体间孔隙越大,水化完全后晶层间距越大,但膨胀力越低.
Yong等[25,29]利用前人测得的膨润土晶层间距结果,分别采用Olphen、DLVO和Gouy-Chapman模型,计算得到膨润土的最终膨胀力,结果如图7所示.3种模型的计算结果表明,膨润土完全水化后的最终膨胀力,均随着最终状态晶层间距的增大而减小,主要原因是膨润土中集合体间孔隙越大,即干密度越小,水化过程中晶层间能够吸收的水分子数就越多,最终晶层间距就越大,膨胀力则越低.Olphen模型计算值过少不具有参考价值,Gouy-Chapman模型和DLVO模型的计算值与试验结果较为吻合,说明该两种模型适用于预测膨润土完全水化后的最终膨胀力.
3.2 扩散双电层厚度对膨胀力的影响
为研究扩散双电层厚度对膨胀力的影响规律,Liu[13]假设蒙脱石水化完全,土颗粒中层叠体充分开裂成单层晶层或数个晶层的堆叠,构建了蒙脱石微观模型(见图8),用于计算扩散双电层厚度,得到如下公式[13]:
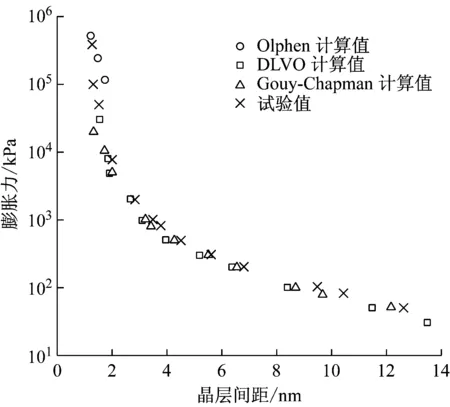
图7 晶层间距对膨胀力的影响Fig.7 Effect of crystalline interlayer distance on swelling pressure
h=nsδsem-(ns-1)dm
(40)
式中:h为扩散双电层厚度;ns为层叠体中晶层数量;δs为晶层厚度;em为蒙脱石孔隙比;dm为晶层间距.
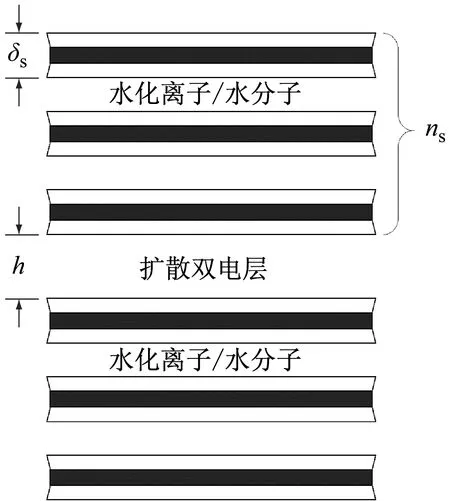
图8 蒙脱石微观模型Fig.8 Montmorillonite microstructure model
Liu[13]利用该模型,将Gouy-Chapman模型中的晶层间距与膨胀力的关系转化为扩散双电层厚度与膨胀力的关系,结果见图9.图9表明,完全水化饱和后的膨润土,最终膨胀力随着扩散双电层厚度的增大而不断减小,模型计算值与试验值基本吻合.这是由于在低干密度下,集合体间孔隙丰富,得以充分形成扩散双电层,与Liu的蒙脱石微观模型计算公式适用条件一致,从而能够准确估算出相应的扩散双电层厚度.
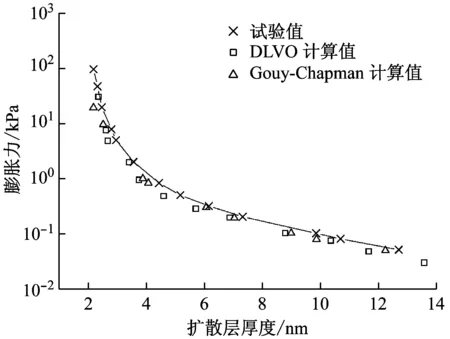
图9 膨胀力与扩散双电层厚度的关系Fig.9 Swelling pressure versus DDL thickness
3.3 初始干密度对膨胀力的影响
大量试验表明,膨润土最终膨胀力与其初始干密度呈指数关系.Tripathy等[36]围绕Gouy-Chapman模型进行了一系列探究,通过式(26)~(28),假设不同膨胀力P值(50~400 kPa),反算出u值,建立u-Kd经验关系式,结果见表1.

表1 不同膨润土的u-Kd拟合关系式Tab.1 u-Kd fitting formula for different bentonite
基于以上u-Kd经验关系式分别计算了MX80、FEBEX、Montigel 3种膨润土的最终膨胀力,并与试验结果进行对比分析,结果如图10所示.由图可知,3种膨润土在干密度小于1.6 g·cm-3时拟合效果较好,但对于干密度大于1.6 g·cm-3的膨润土,试验结果远大于预测值.显然,此公式适用范围应为低膨胀力阶段即低干密度.对高干密度试样,由于孔隙空间有限,扩散双电层发展不完全,由此产生的渗透膨胀力远小于最终膨胀力.
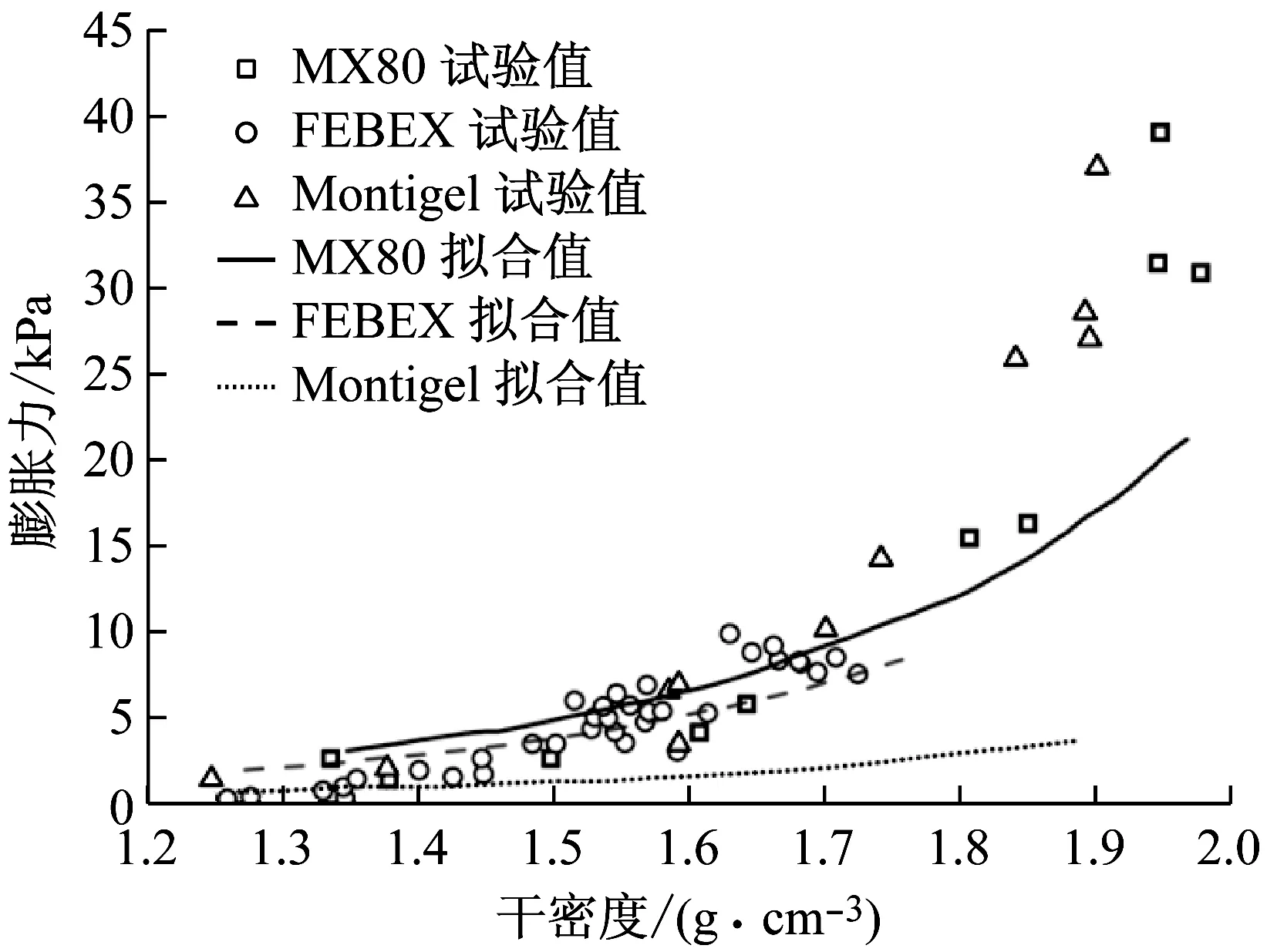
图10 初始干密度对膨胀力的影响Fig.10 Effect of initial dry density on swelling pressure
根据式(25)知,干密度与晶层间距一一对应,可由干密度计算Kd值;将试验值P代入式(28)得到u值,即可得新的u-Kd关系式
u=-7.277 lg(Kd)-2.91
(41)
u=-10.427 lg(Kd)-7.72
(42)
u=-9.1.90 lg(Kd)-3.26
(43)
Tripathy等[36]利用式(41)~(43),重新进行了计算,结果见图11.对比图10和图11可见,计算值与试验值拟合度明显提高.

图11 膨润土膨胀力修正计算值与试验值Fig.11 Experimental and theoretical swelling pressures
3.4 离子类型对膨胀力的影响
在实际工程中,含有一定化学成分的地下水会进入膨润土中,进而对膨润土的性质产生影响.膨润土在水化过程中,不同离子的水化能差异导致膨胀势能不同.大量试验表明,相同干密度条件下,钙基膨润土的膨胀力大于钠基膨润土的膨胀力.据此,Liu[13]推测饱和状态下钠基膨润土层叠体的晶层数量为1.5,而饱和状态下钙基膨润土层叠体的晶层数量为2.5,并对Wyoming钠基膨润土(WyNa)和钙基膨润土(WyCa)进行了计算,结果见图12.
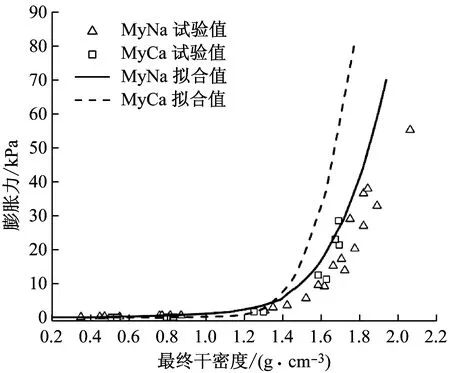
图12 离子类型对膨胀力的影响Fig.12 Effect of ion type on expansion force
不难发现,当干密度小于1.4 g·cm-3时,钠基膨润土和钙基膨润土膨胀力的计算值与试验值吻合较好;当干密度大于1.4时,钠基膨润土膨胀力计算值与试验值基本吻合,但钙基膨润土的计算值与试验值差异明显,表明高压实状态下钙基膨润土ns取值有待进一步论证.
3.5 模型误差分析
根据前文分析可知,不同模型的计算结果与试验值的吻合程度不同.一方面,前述模型大多是针对散状膨胀土所建立的预测公式,对于低干密度压实膨润土而言,水化时扩散双电层发展较完全,因此计算结果与试验值吻合较好;对于高干密度压实膨润土而言,集合体间的孔隙明显减少,水化过程中集合体周围的扩散双电层不能充分发展,膨胀过程以晶层膨胀为主,渗透膨胀受到抑制,导致计算结果误差相对较大.另一方面,模型计算时,公式中的一些指标参数,如孔隙比e、晶层间距d、比表面积S等是取自压实膨润土的初始状态值,而计算得到的膨胀力是水化后的最终状态值,忽略了压实膨润土水化膨胀过程对参数的影响,导致计算结果偏差增大.
4 结论
本文结合膨润土水化膨胀机理,回顾和总结了膨胀力的预测机理、理论模型及试验验证的最新研究成果.针对高压实膨润土膨胀力预测的研究已经取得一些成果,为今后进一步研究奠定了基础.例如扩散双电层模型的预测结果与扩散双电层发展完全的试样的试验结果具有良好的一致性,而对于扩散双电层发展不完全的土样还未有针对性的研究.同时,在处置库长期运营中,影响膨润土膨胀力的因素众多,目前的模型研究多仅考虑了水力的耦合场,而温度、外界环境离子的进入等因素还缺乏相关研究.

