不同环境风向和风速下两种直接空冷凝汽器单元换热性能的仿真对比

王 涛， 阴继翔， 贺小怡

(太原理工大学 电气与动力工程学院， 山西 太原 030024)

0 引 言

近年来， 电力工业发展迅猛， 截至2016年底， 我国煤电在全国发电装机容量的占比达到57.33%[1]. 而我国煤炭资源主要分布于北方水资源匮乏地区， 直接空冷机组由于其良好的节水性能在该类地区得到了广泛应用. 根据直接空冷机组长期的运行经验， 当地环境风的风向和风速是影响机组安全经济运行的主要因素.

为降低环境风对直接空冷凝汽器换热性能的影响， 国内外许多学者在此方面做了大量研究. Borghei L等[2]模拟了空冷岛在两种环境风向下的换热性能， 结果表明空冷岛的热风回流随环境风速的增大而增大. 何伟峰等[3]通过在空冷凝汽器翅片管内加载凝结程序的方法， 对不同环境风温、 风速下的直接空冷单元进行了数值研究. 张学镭等[4-5]为削弱环境横风对空冷凝汽器换热性能的影响， 分别提出在空冷单元底部加装一种进风扩压装置和导流叶栅来提高空冷单元的换热效率. 程友良等[6]通过在空冷单元内部加装结合形导流板来改善空冷单元内部的空气流场， 以提高空冷凝汽器的换热效果. 以上学者都是针对“Λ”型布置方式的直接空冷凝汽器展开研究， 而杨建国等[7]提出一种新的“V”型布置方式的直接空冷单元. 陈磊[8]对一种由引风式“V”型空冷单元组成的空冷岛进行了数值研究， 发现在环境风的影响下， 空冷岛迎风侧空冷单元的换热性能得到了显著改善. Zhang等[9]研究了迎面速度分布对两种不同布置方式的直接空冷凝汽器换热的影响， 并通过数值模拟指出， “V”型直接空冷凝汽器单元内部的速度分布更加均匀.

前人的研究主要局限于环境风对“Λ”型直接空冷凝汽器换热性能的影响， 而对于新提出的“V”型直接空冷凝汽器的研究还不够深入. 本文在现有研究的基础上， 利用FLUENT软件对两种不同布置方式的直接空冷凝汽器单元进行数值模拟， 对比分析了环境风对两种直接空冷凝汽器单元换热性能的影响， 为强化直接空冷单元的换热性能提供有价值的理论依据.

1 物理模型及计算方法

1.1 几何模型及网格划分

图 1 为“V”型和“Λ”型直接空冷单元的结构示意图. 两种直接空冷单元的结构尺寸为11.3 m×11.5 m×13.84 m， 风机直径为9.14 m， 换热器采用扁平蛇形翅片结构， 空冷平台距地面高度为40 m， 两种直接空冷单元的计算域为91.3 m×91.5 m×93.84 m.

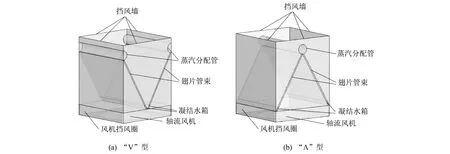
图 1 两种直接空冷单元的结构示意图Fig.1 Structure schematic diagram of two direct air-cooled units

用Gambit软件建立几何模型并对计算区域采用分块划分的方法进行网格化. 将计算域分为27个区域， 空冷单元内部不规则的区域采用四面体网格划分， 其它区域均采用六面体网格， 并对空冷单元进行网格加密(见图 2). “V”型直接空冷凝汽器计算域的网格划分如图 3 所示. “Λ”型直接空冷凝汽器计算域的网格划分方法与“V”型直接空冷凝汽器相同， 为节省篇幅， 此处不再提供其网格划分示意图.

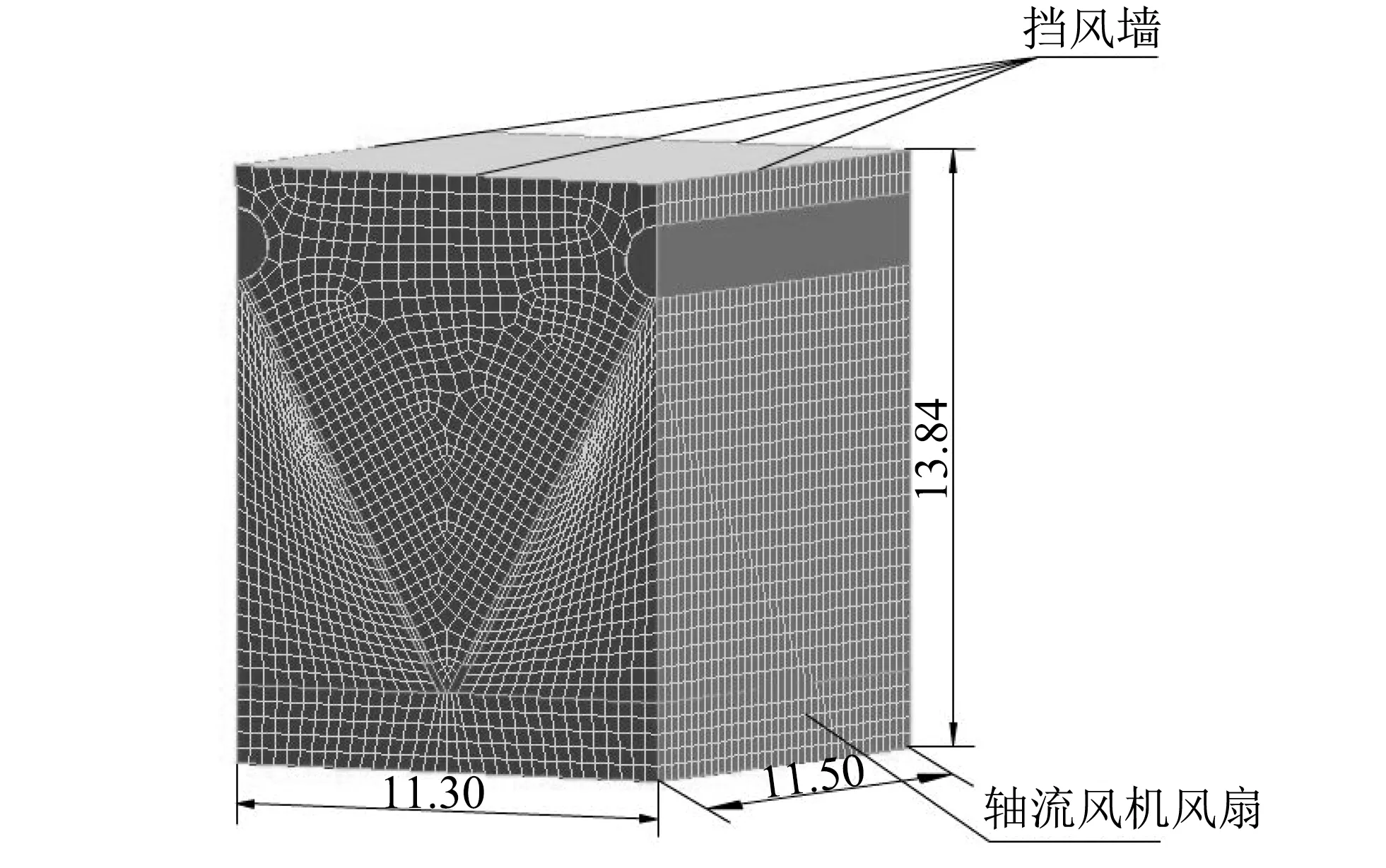
图 2 “V”型直接空冷单元的网格划分Fig.2 Meshing of “V” type direct air-cooled unit

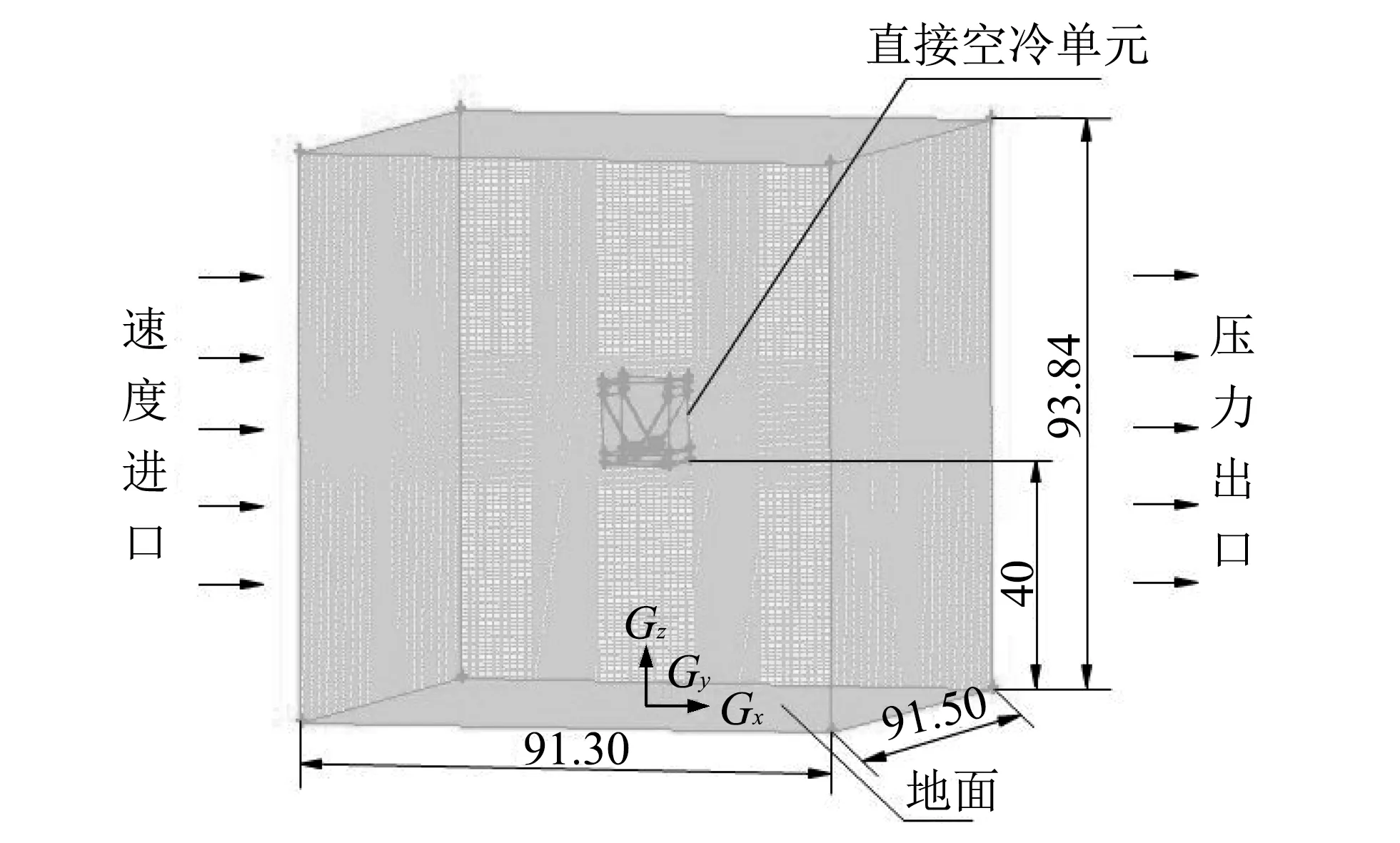
图 3 “V”型直接空冷凝汽器的计算域Fig.3 The computational domain of “V” type direct air-cooled condenser

1.2 控制方程及边界条件

标准k-ε湍流模型在工程流场和热交换模拟中具有广泛的应用， 因此本文采用标准k-ε湍流模型来模拟空冷单元内空气的流动. 假设计算域内的流动为不可压缩的定常流动， 不考虑辐射换热， 控制方程见文献[10]. 压力和速度的耦合使用Simple算法， 各计算方程的收敛指标为： 连续性方程为10-5， 动量方程及能量方程为10-7，k-ε方程为10-7.

采用Patankar[11]提出的多孔介质模型模拟空气流过翅片管束产生的阻力变化， 将流过翅片管束的流动阻力看作是附加在动量方程的动量源项， 源项包括黏性损失和惯性损失两项， 描述为

(1)

式中：ni为i方向的速度；a为渗透率； 黏性阻力系数μ和惯性阻力系数C2参考文献[12]的实验数据. 翅片管束的换热采用Fluent中的散热器模型， 设置为散热器边界[13].

风机采用集总参数的思想简化为一个薄面， 风机的性能曲线采用霍林河电厂空冷风机的性能曲线， 通过对轴流风机的静压与流量的性能曲线进行拟合， 得出风机静压变化与速度之间的多项关系式

Δp=234.96-17.86n+1.185n2-0.135n3.(2)

计算模型进口采用速度入口边界条件， 风速沿高度的变化规律服从幂指函数分布[13]

u=u10(z/10)a,(3)

式中：u为沿高度方向的风速；u10为距地面10 m高度处的平均风速， 模型中分别取1, 3, 5, 7, 9, 11 m/s；z为高度；a为地面粗糙度， 本文取为0.2. 出口采用压力出口边界条件， 计算区域底部为地面， 设为等温边界条件， 取为293 K.

模型中蒸汽分配管和凝结水箱为恒壁温边界条件， 分别取为330 K和320 K， 空冷单元四周的挡风墙和轴流风机风筒定义为无滑移的耦合壁面(见图 2)， 计算域的其它面取为对称边界条件.

1.3 网格无关性验证

为确保计算的准确性， 对不同网格数目下的“V”型直接空冷单元进行数值模拟， 轴流风机出口空气流量变化如图 4 所示. 由图可知， 当网格数为8.62×105时， 风机出口流量已基本保持不变. 网格数为8.62×105与网格数为1.443 1×106时的计算结果相比， 风机的出口流量低了0.33%. 为节省计算成本， 并确保模型的计算精度， 本文采用8.62×105的网格数进行计算.

图 4 风机出口流量与网格数量的关系Fig.4 The relationship between the outlet flow of fans and the number of grids

1.4 数据处理

空气侧的吸热量为

Qa=Gacp(ta2-ta1),(4)

式中：Qa为管外空气侧吸热量， MW；Ga为空气质量流量， kg/s；cp为空气的定压比热容， kJ/(kg·K)；ta1和ta2分别为管束入口和出口空气温度， K.

凝汽器空气侧的表面对流换热系数为

(5)

式中：h0为凝汽器空气侧的表面对流换热系数， W/(m2·K)；Ar和Af分别为扁平管面积和翅片面积， m2；hf为翅片取顶端温度时的翅片效率， 其计算方法见文献[14]中的公式(2-40)， 不同工况下的翅片效率可以通过迭代来获得； Δtm为空气侧对流换热的对数平均温差， K.

空气侧对流换热的对数平均温差为

(6)

式中：tt为管壁的平均温度， K.

1.5 模型验证

为验证本文计算方法的准确性， 对文献[10]所研究的“Λ”型直接空冷单元进行数值模拟， 并将计算结果与文献提供的数据进行对比. 表 1 为文献[10]中直接空冷单元的散热量与轴流风机进风量的实验数据， 表2为相应工况下的数值模拟结果. 取相同的环境温度和环境风速时， 数值模拟结果在设计工况下与实验结果相比误差最小， 风机进风量和空冷单元散热量的误差分别为1.1%和6.3%； 数值模拟结果在实验1工况下与实验结果相比误差最大， 风机进风量和空冷单元散热量的误差分别为1.3%和13.7%. 分析模拟结果与实验结果基本吻合， 可见本文的模型及算法有效可靠.

表 1 “Λ”型直接空冷单元的实验结果

表 2 “Λ”型直接空冷单元的数值模拟结果

2 计算结果分析

规定垂直于直接空冷单元蒸汽分配管的环境风为X风向， 平行于直接空冷单元蒸汽分配管的环境风为Y风向， 沿正X和正Y之间45°方向的斜向风为45°风向. 空冷单元在Y=0截面的流场取计算域Y轴的中剖面， 出口速度分布取平行于翅片管束20 cm高度处的斜截面.

2.1 两种空冷单元在X环境风向下的流场分析

在环境风速为11 m/s时， 图5(a)和图5(b)分别为“Λ”型和“V”型空冷单元在Y=0截面处的内部流场， 图6(a)和图6(b)分别为“Λ”型和“V”型空冷单元的出口速度分布.

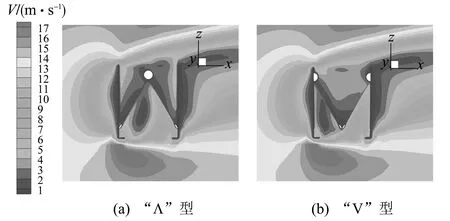
图 5 两种空冷单元在环境风速为11 m/s时Y=0截面处的速度场Fig.5 The velocity field at Y=0 cross section of two air-cooled units at ambient wind speed of 11 m/s

对比分析图 5 可知， 在环境风速为11 m/s时， 当环境风沿正X方向掠过时， 两种空冷单元迎风侧(左侧)翅片管束内部均出现流场恶化现象. 对于“Λ”型空冷单元， 其内部的流动空间是相连通的， 流场的恶化不仅降低了其迎风侧(左侧)翅片管束内部的空气流速， 也使其背风侧(右侧)翅片管束顶部的空气流速下降， 导致“Λ”型空冷单元左右两侧翅片管束的出口速度明显下降(见图 6)， 不利于空气的热交换， 从而使空冷单元的换热性能下降. 而对于“V”型空冷单元， 由于翅片管束将空冷单元内部的流动空间分隔为左右两个部分， 流场的恶化只对迎风侧(左侧)翅片管束造成影响， 使迎风侧翅片管束的出口速度下降， 对背风侧(右侧)翅片管束的出口速度影响较小(见图 6). 可见，X风向的环境风对“Λ”型空冷单元的影响比“V”型空冷单元大.

图 6 两种空冷单元在环境风速为11 m/s时的出口速度分布Fig.6 Distribution of outlet velocity for two air-cooled units at an ambient wind speed of 11 m/s

2.2 X风向环境风对两种空冷单元换热性能的影响

如图 7 为两种直接空冷单元在X环境风向下风机的进风量随环境风速的变化关系.

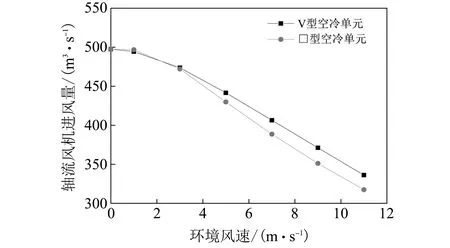
图 7 风机进风量随环境风速的变化Fig.7 Fan flow changes with the ambient wind speed

由图 7 可知， 随着环境风速的增大， 两种空冷单元风机的进风量都呈下降趋势， 且在环境风速较大时近似呈线性规律变化. 当环境风速为3 m/s 时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高1.67 m3/s； 当环境风速为11 m/s时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高18.73 m3/s. 可见， 随着环境风速的增大， “V”型空冷单元与“Λ”型空冷单元风机进风量之间的差距逐渐增大， 且“V”型空冷单元的风机进风量较高， 这是因为环境风在X来流方向时， “V”型空冷单元迎风侧(左侧)翅片管束阻碍了其内部涡流区向空冷单元右侧流动空间的进一步发展， 从而降低了涡流对风机进口气流的扰动， 而背风侧(右侧)翅片管束对空冷单元右侧流动空间内的气流有一定的引导作用， 可以提升风机的进风量， 且在环境风速越大时， 这种作用越明显.

X风向的环境风对两种直接空冷单元换热量和空气侧的对流换热系数的影响如图 8 和图 9 所示. 从图中可以看出， 在X环境风向下， 两种空冷单元的换热量和空气侧的对流换热系数都随环境风速的增大而降低， 且“Λ”型空冷单元的换热量和空气侧对流换热系数的最大降幅分别为 34.02%和35.4%， 而“V”型空冷单元的最大降幅分别为30.75%和32.25%. 可见，X风向的环境风对“Λ”型空冷单元换热性能的影响较大， 而“V”型空冷单元的换热性能在X环境风向的影响下表现得更稳定.

图 8 两种空冷单元换热量与环境风速的关系Fig.8 Relationship between heat transfer capacity and ambient wind speed of two air-cooled units

图 9 两种空冷单元空气侧对流换热系数与环境风速的关系Fig.9 Relationship between air convection heat transfer coefficient and ambient wind speed of two air-cooled units

由图可知， 当环境风速小于3 m/s时， “V”型空冷单元的换热量和空气侧对流换热系数略小； 而随着环境风速的进一步增大， “V”型空冷单元的换热量和空气侧对流换热系数逐渐高于“Λ”型空冷单元. 在环境风速为11 m/s时， 两种空冷单元换热性能之间的差距最大， 此时， “V”型空冷单元和“Λ”型空冷单元的换热量分别为12.46 MW和11.92 MW， 前者较后者的换热量提升了4.5%； “V”型空冷单元和“Λ”型空冷单元的空气侧对流换热系数则分别为18.35 W/(m2·K)和17.63 W/(m2·K)， 前者较后者的对流换热系数提升了4.08%. 由此可见， 当X风向的环境风速较大时， “V”型空冷单元比“Λ”型空冷单元的换热性能好.

2.3 两种空冷单元在Y环境风向下的流场分析

在环境风速为11 m/s时， 图10(a)和图10(b) 分别为“Λ”型和“V”型空冷单元在Y=0截面处的内部流场， 图11(a)和图11(b)分别为“Λ”型和“V”型空冷单元的出口速度分布.

图 10 两种空冷单元在环境风速为11 m/s时Y=0截面处的速度场Fig.10 The velocity field at Y=0 cross section of two air-cooled units at ambient wind speed of 11 m/s

图 11 两种空冷单元在环境风速为11 m/s时的出口速度分布Fig.11 Distribution of outlet velocity for two air-cooled units at an ambient wind speed of 11 m/s

由图 10 可知， 在Y环境风向的影响下， “Λ”型空冷单元内部的低流速区更为明显， 其内部的空气流速明显比“V”型空冷单元小， 这表明“Λ”型空冷单元内部的空气流动受环境风的影响更为敏感. 对比“V”型空冷单元左右两侧翅片管束内部的速度分布可知， 其左侧翅片管束内部的流速较高. 由于翅片管束将“V”型空冷单元内部的流动空间分隔为左右两个部分， 而空冷单元内部的空气在风机的作用下旋转上升， 这就使得空气在“V”型空冷单元内部左右两侧空间内的旋转方向不一致. 在空冷单元右侧， 气流的旋转方向与环境风的来流方向一致， 降低了这一侧的空气流量， 从而使这一侧出现流场恶化， 这也导致了“V”型空冷单元右侧翅片管束的出口速度高于左侧(见图 11).

对于“Λ”型空冷单元， 在环境风与风机的共同作用下， 其内部的流场恶化也靠近右侧翅片管束， 而由于其内部的流动空间是连通的， 从而使内部的流场恶化对左右两侧翅片管束都造成很大影响， 这也导致了“Λ”型空冷单元左右两侧翅片管束的出口速度均下降， 且近似呈对称分布(见图 11). 因此， 相比于“Λ”型空冷单元， “V”型空冷单元在一定程度上可以减小Y风向环境风的扰动.

2.4 Y风向环境风对两种空冷单元换热性能的影响

两种直接空冷单元在Y风向下的风机进风量随环境风速的变化关系如图 12 所示.

图 12 风机进风量随环境风速的变化Fig.12 Fan flow changes with the ambient wind speed

由图 12 可知， 当环境风速小于3 m/s时， 两种空冷单元风机进风量的下降趋势较缓； 而随着环境风速的进一步增大， 两种空冷单元风机进风量的下降趋势都呈线性规律变化. 当环境风速为3 m/s 时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高 8.52 m3/s； 当环境风速为9 m/s时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高 8.68 m3/s. 可见， 在环境风速较大时， 两种空冷单元风机进风量之间的差距基本保持不变， 这是因为“V”型空冷单元内部的气流在Y环境风向的影响下表现的比“Λ”型空冷单元更稳定， 减小了空冷单元内部空气流动对风机进口气流的扰动， 从而使“V”型空冷单元风机进风量高于“Λ”型空冷单元.

如图 13 和图 14 分别为两种直接空冷单元在Y风向下的换热量和空气侧的对流换热系数与环境风速的关系曲线. 由图可知， 两种直接空冷单元的换热量和空气侧对流换热系数都随环境风速的增大而降低， 且“Λ”型空冷单元换热量和空气侧对流换热系数的最大降幅分别为32.14%和33.55%， 而“V”型空冷单元的最大降幅分别为30.64%和31.79%. 可见，Y风向的环境风对“V”型空冷单元换热性能的影响比“Λ”型空冷单元小.

图 13 两种空冷单元换热量与环境风速的关系Fig.13 Relationship between heat transfer capacity and ambient wind speed of two air-cooled units

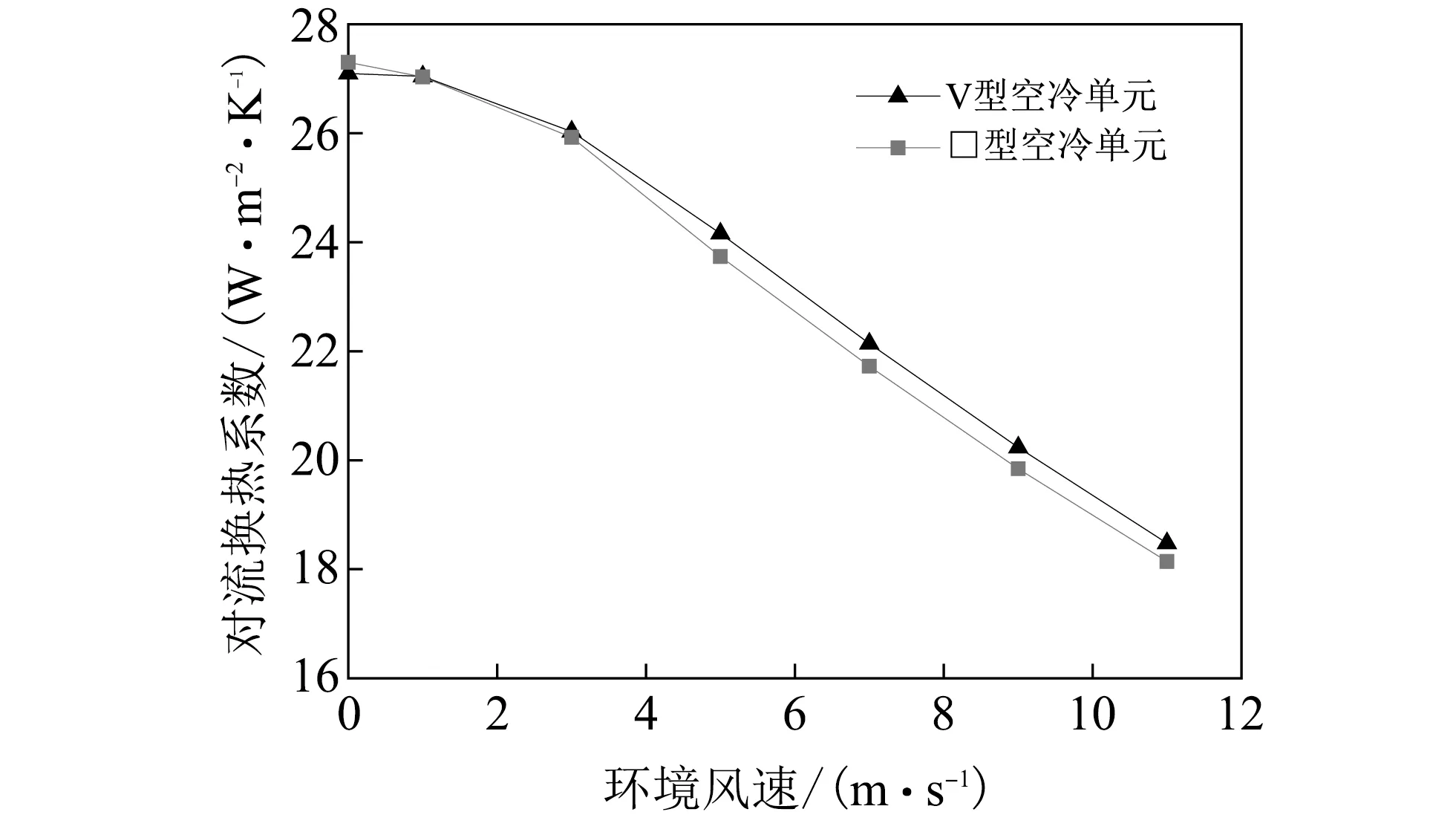
图 14 两种空冷单元空气侧对流换热系数与环境风速的关系Fig.14 Relationship between air convection heat transfer coefficient and ambient wind speed of two air-cooled units

由图可知， 当环境风速大于3 m/s时， “V”型空冷单元的换热量和空气侧对流换热系数比“Λ”型空冷单元高. 在环境风速为9 m/s时， “V”型空冷单元的换热量和空气侧对流换热系数分别为13.65 MW和20.23 W/(m2·K)； 而“Λ”型空冷单元的换热量和空气侧对流换热系数分别为13.38 MW和19.84 W/(m2·K). 此时， 两种空冷单元之间的换热量和空气侧对流换热系数相差最大， “V”型空冷单元的换热量和空气侧对流换热系数比“Λ”型空冷单元分别高2%和1.97%. 因此， 当Y环境风向的风速较大时， “V”型空冷单元的换热性能比“Λ”型空冷单元好.

2.5 两种空冷单元在45°环境风向下的流场分析

在45°风向下， 当环境风速为11 m/s时， 图15(a)和图15(b)分别为“Λ”型和“V”型空冷单元在Y=0截面处的内部流场， 图16(a)和图16(b)分别为“Λ”型和“V”型空冷单元的出口速度分布.

图 15 两种空冷单元在环境风速为11 m/s时Y=0截面处的速度场Fig.15 The velocity field at Y=0 cross section of two air-cooled units at ambient wind speed of 11 m/s

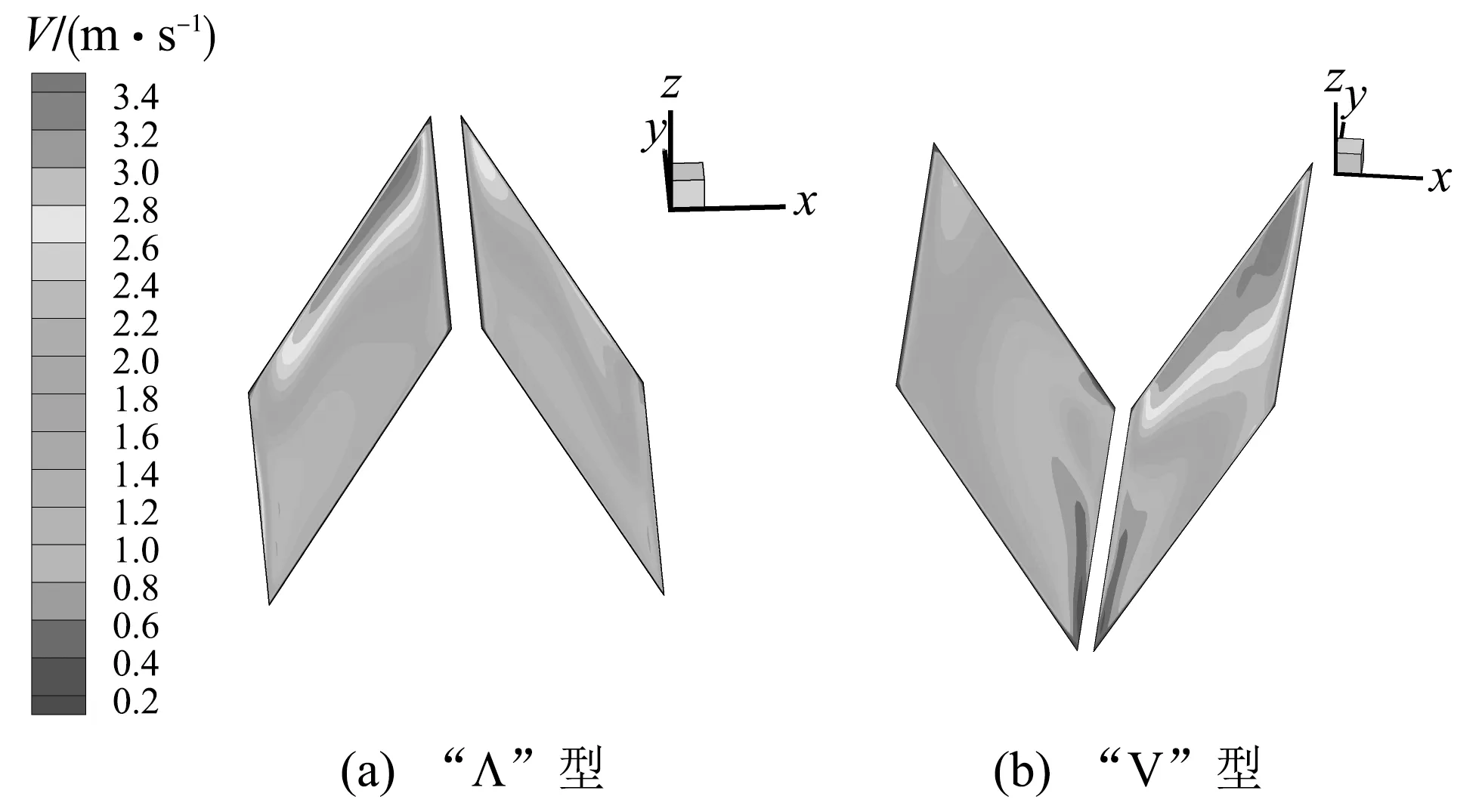
图 16 两种空冷单元在环境风速为11 m/s时的出口速度分布Fig.16 Distribution of outlet velocity for two air-cooled units at an ambient wind speed of 11m/s

由图15可知， 在45°环境风向的影响下， 两种空冷单元内部均出现大面积的流场恶化， 这主要是因为环境风使轴流风机的入口产生流动畸变， 使空冷单元内部产生涡流， 从而导致空冷单元内部出现流场恶化. “Λ”型空冷单元内部的流场恶化位于其中部偏左的位置， 这使得空冷单元左右两侧翅片管束均受到影响， 导致其左右两侧的出口速度明显下降(见图16)， 不利于空气的热交换， 从而降低“Λ”型空冷单元的换热性能. 而“V”型空冷单元内部的流场恶化位于其左侧， 主要降低了其左侧翅片管束的出口速度(见图16)， 这是因为“V”型空冷单元内部左侧的流动空间位于45°环境风向的迎风侧， 导致环境风对此部分的影响较大. 由此可见， 45°风向的环境风对“Λ”型空冷单元内部的空气流动扰动较大， 从而导致其换热性能比“V”型空冷单元差.

2.6 45°风向环境风对直接空冷单元换热性能的影响

在45°环境风向下， 两种直接空冷单元风机的进风量随环境风速的变化关系如图17所示. 由图可知， 随着环境风速的增大， 两种空冷单元风机的进风量都呈下降趋势. 当环境风速为3 m/s时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高4.27 m3/s； 当环境风速为11 m/s时， “V”型空冷单元比“Λ”型空冷单元风机的进风量高16.9 m3/s. 可见， 随着环境风速的增大， 两者风机进风量之间的差距逐渐变大， 这是因为环境风速越大， “Λ”型空冷单元内部产生的涡流比“V”型空冷单元越剧烈， 而涡流会对风机进口的气流造成很大扰动， 从而使“Λ”型空冷单元风机进风量的下降幅度更大.

图 17 风机进风量随环境风速的变化Fig.17 Fan flow changes with the ambient wind speed

如图 18 和图 19 分别为两种直接空冷单元在45°环境风向下的换热量和空气侧的对流换热系数随环境风速的变化关系. 由图可知， 两种空冷单元的换热量和空气侧的对流换热系数都随环境风速的增大而降低， 且“Λ”型空冷单元的换热量和空气侧对流换热系数的最大降幅分别为34.79%和35.5%； 而“V”型空冷单元的最大降幅分别为31.57%和32.9%. 可见， “Λ”型空冷单元的换热性能受45°风向环境风的影响比“V”型空冷单元更敏感.

从图中可以看出， 当环境风速大于3 m/s时， “V”型空冷单元的换热量和空气侧对流换热系数比“Λ”型空冷单元高， 且随着环境风速的增大， 两种空冷单元之间的换热量和空气侧对流换热系数差距逐渐变大. 在环境风速为11 m/s时， “V”型空冷单元的换热量和空气侧对流换热系数分别为12.32 MW和18.18 W/(m2·K)， 而“Λ”型空冷单元的换热量和空气侧对流换热系数分别为11.79 MW 和17.41 W/(m2·K). 此时， 两种空冷单元之间的换热量和空气侧对流换热系数相差最大， “V”型空冷单元的换热量和空气侧对流换热系数比“Λ”型空冷单元分别高4.49%和4.42%. 因此， 当45°环境风向的风速较大时， “V”型空冷单元的换热性能比“Λ”型空冷单元好.

图 18 两种空冷单元换热量与环境风速的关系Fig.18 Relationship between heat transfer capacity and ambient wind speed of two air-cooled units

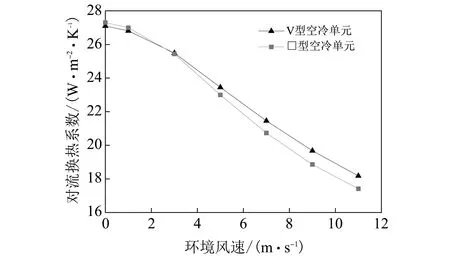
图 19 两种空冷单元空气侧对流换热系数与环境风速的关系Fig.19 Relationship between air convection heat transfer coefficient and ambient wind speed of two air-cooled units

3 结 论

通过对两种直接空冷单元在不同环境风向下的换热性能和流场的对比分析， 得出以下结论：

1) 在不同环境风向的影响下， 两种空冷单元内部均出现了不同程度的流场恶化现象. “Λ”型空冷单元内部的流场恶化对其左右两侧的翅片管束均会造成影响， 而“V”型空冷单元左右两侧翅片管束受流场恶化的影响比“Λ”型空冷单元小.

2) “V”型空冷单元受环境风的扰动比“Λ”型空冷单元更小， 换热性能更稳定.

3) 与“Λ”型空冷单元相比， “V”型空冷单元在环境风速较大时的换热性能较好， 其换热量在X风向、Y风向和45°风向下最高比“Λ”型空冷单元分别高4.5%、 2%和4.49%.