CRFID中的能量管理与任务规划算法研究

郭茹茹， 巩建平， 赵菊敏， 李灯熬， 朱飑凯

(太原理工大学 信息与计算机学院， 山西 晋中 030600)

0 引 言

射频识别(RFID)系统中标签是其一个重要的组成部分， 标签可以从阅读器中收集能量并且进行通信. 随着RFID技术的发展， 之前的有源标签因其体积大， 寿命短而逐步被无源标签所取代. 相比之下， 无源传感器标签接收来自RFID阅读器的能量而不受电池寿命的限制， 使其可以永久地嵌入物体中， 对物体进行监测， 像建筑物结构体的监测， 医疗监测等. 另一个优点是它们重量轻， 体积小， 成本低. 但是纯无源传感器标签的限制是必须靠近RFID阅读器. 因为需要通过阅读器来提供能量， 供其工作.

进一步的考虑是RFID传感器标签的可配置性和计算能力. 现有普通无源标签都是只有感知能力而不具备计算能力. 而CRFID是集感知与计算为一体的无源标签， 其包括两种平台： WISP与MOO[1]. 本文主要是针对无线识别和传感平台(WISP)来进行算法的设计. WISP是一种可编程的、 无源感知和计算的平台， 它利用一个16位的低功耗微处理器进行感知和计算. 它的能量来源是远程的RFID阅读器. 与RFID一样执行EPC标准， 是可以被RFID阅读器识别的被动标签， 但是与普通RFID不同的是， 其具有感知和计算能力. 由于自身集成三轴加速度与温度传感器使其可以进行感知， 内置MSP430处理器使其可以进行计算. 其中MSP430是WISP的控制核心器件， 包括对能量的控制， 并且 WISP 还外接各类传感器， 应用范围比传统的RFID更广泛.

WISP通信原理主要是通过反向散射和改变天线的阻抗， 从而改变入射信号的接收强度来实现的. 当一个发射波碰到具有不同阻抗值的两种介质之间的边界时， 波会被反射回去. 不同的天线阻抗， 会有不同的反射量. 所以利用这一特点， 通过调制在天线端口的阻抗可以控制入射RF能量的分散量， 从而实现信息的调制和传送.

之前解决能量问题的方法主要有硬件的改进与能量管理算法的设计两部分. 其中在硬件能量优化方面， 华盛顿大学的Ransford B等人[2]在2008年通过插入检查点以及硬件中断的方法来控制WISP的工作状态， 从而增加能量利用率； 2009年， 马萨诸塞大学Sample A P等人[3]提出了一种将电容式触摸界面与无源RFID标签相结合的方法. 该方法将WISP标签制作成一个具有电容感知能力的无源超高频标签， 并将其集成到标签天线的端口. 使得WISP天线既可以作为一个电容式触摸传感器， 利用天线的低频自电容作为电场触摸或传感器来进行通信， 又可以作为UHF 的RFID天线来提供电源. 当用户触摸在标签天线上的输入区域时， 电容传感器的RC时间常数被测量到， 与此同时， 触摸事件传给阅读器. 此方法将传感器与微控制器分开， 直接将数据传给阅读器， 节省了能量的消耗. 2010年， 华盛顿大学团队[4]提出了混合的能量源， 将太阳能板与WISP结合， 增加了WISP的能量收集. 从2014年开始， 为了打破WISP只收集 915 MHz 能量的局限， 华盛顿大学的Aaron N. Parks等人[5]， 对WISP的射频前端电路进行了改进， 主要是增加了收集能量的频段， 使WISP可以收集更多的能量. 2015年华盛顿大学的Vamsi Talla等人[6]继续改进WISP的射频前端， 设计了可以收集WIFI中能量的芯片， 因为WIFI覆盖的范围很广， 如果可以收集到WIFI中的能量， 也是对WISP能量管理上的一个很大突破. 2016年， 华盛顿大学的Liu Q等人[7]又将WISP设计成手机蓝牙中的能量， 不仅增加了WISP的能量源， 又为WISP在手机中的应用提供了思路. 张宏等[8]设计出了比WISP能量收集更多的MOO. 通过改变存储器来解决了断电不丢失的问题， 但是能量的消耗却增加了. 在硬件方面对于WISP 的改进也一直在继续着， 但是硬件的改进需要很大的成本.

浙江大学的陈积明教授以及其团队目前主要研究的方法是通过能量源的移动策略来提高能量的收集以及能量的利用率[9]而且侧重点只是偏向静态的能量模型[10]以及通信的延迟[11]， 并没有对任务进行规划. Massachusetts大学团队研究出了比特-比特传输[12]， 通过数据包的切割来节省能量. 在此基础上， 赵彤, 杨文国等人首次在传感网中提出了基于能量的数据包调整算法[13]. 李虹等人[14]提出了睡眠机制来对能量进行了管理. Fu L等人[11]采用了最优的吞吐量的能量管理策略， 并减少了传输数据的延迟. 提出了全新的动态电压调节的管理技术， 即根据负载情况动态调整微处理器的电源电压. Buettner, Michael等[15]提出了具有Inter WISP的RFID传感器网络的原形， 但是要实现它并不简单. Roy, Sumit等[16]通过进一步的分析， 认为RFID传感器网络的设计必须考虑到克服链路层缺点. 例如， 标签的功能少， 能量有限， 几乎都是依靠阅读去实现的， 所以导致了上下链路在传数据时会发生碰撞. 同时由于一个区域内会有多个阅读器， 阅读器也会发生碰撞. 这些为基于WISP的RFID传感器网络发展和研究指明了方向.

以上方法想要从两个角度解决节点中能量的问题， 但是能量利用率的提升并不大， 对于能量管理， 如果将其量化， 再进行管理是一个很有效的方法. 本文将建立WISP的能量模型， 并且在此基础上进行能量的管理与任务的同步规划.

1 能量模型

反向散射是通过阅读器向无源设备提供能量， 标签端进行反向散射来实现通信. 阅读器通过发送CW波来给标签提供能量， 无源标签通过反向散射将信息传递到阅读器， 从而实现通信. 在整个通信过程中， 由于标签是属于被动式的， 尤其是能量， 完全是靠阅读器来提供， 所以能量显得尤为重要， 但是目前对于CRFID并没有一套完整的能量模型， 只是建立了理想的能量收集模型， 但并没有对能量的消耗建立详细的模型， 为此， 本文对能量进行了详细的建模， 包括接收到的和消耗的能量.

1.1 能量收集模型

文献[11]中提出的能量收集主要是通过天线和整流电路来完成的， 能量最终存储在一个电容里. 理想的模型中主要是利用电磁波传输理论中的弗里斯公式

(1)

式中：PR为接收功率；PT为发射功率；GT为发射端增益；GR为发射端增益；λ为入射波波长. 其中， 接收功率30 dBm(1 W)， 波长为0.33 m, 发射端增益为6 dBi， 接收端增益为2 dBi.

文献[11]中建立模型的前提是在理想环境中， 但是在实际环境中， 空间距离短， 会导致电磁波尺度衰减， 多径效应等问题. 因此弗里斯公式不是CRFID的最佳模型. 根据实际环境对式(1)进行修正， 引入两个参数η，α， 则

(2)

式中：η为修正效率；α为路径损耗. 该修正主要是将弗里斯自由空间转化为适用WISP模型， 通过此模型就可以知道不同距离下所接收到的功率值.

1.2 能量消耗模型

在漏电实验中涉及到了功率的计算问题， 功率P=UI, 不能直接进行测量， 只能通过测试电容两端的电压间接得到. 通过联立式(3)与式(4)可以得到式(5), 这样将电压值与功率值联系起来， 根据测得的电压值就知道漏电功率的值.

I=kCVc,(3)

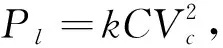
Vt=Vue(-t/τ),(5)

式中：k为介电常数；C为电容值,C=10 μF.

WISP节点工作主要包括： 感知、 计算、 通信. 其中通信消耗的能量最多.

1) 节点采样能耗分析与建模

WISP节点随着采样次数的不同， 采样能耗也不同. 通过采集1 000次的实验得到关系式为

Pp=0.005 049x+0.011 32.(6)

2) 节点计算能耗分析与建模

WISP节点随着计算次数不同， 计算能耗也不同. 通过采集1 000次的实验得到关系式为

Pp=0.000 081x+0.564 6.(7)

3) 节点通信能耗分析与建模

CRFID通信过程主要是通过反向散射来进行的， 反向散射是通过改变天线的阻抗， 从而改变入射信号的接收强度来实现的. 当一个发射波碰到具有不同阻抗值的两种介质之间的边界时， 波会被反射回去. 不同的天线阻抗， 会有不同的反射量. 所以利用这一特点， 通过调制在天线端口的阻抗可以控制入射RF能量的分散量， 从而实现信息的调制和传送. 在反向散射中有两种情况:

① 当电路中的开关为0时， 晶体管关断， 达到阻抗匹配， 多数信号被吸收， 这些能量会被存储于电路的电容中， 用于标签的工作. 反射系数为

(8)

式中：Za为天线的阻抗；ZL1为负载的阻抗.

雷达截面为

(9)

反射能量为

(10)

② 当电路中的开关为1时， 晶体管处于导通阶段， 阻抗不匹配， 天线会反射能量， 产生一个较大振幅的散射信号， 这样只能收集到较少的能量. 反射系数为

(11)

雷达截面为

(12)

反射能量为

(13)

通过模型的建立可以实时地知道不同位置下标签的剩余能量值， 从而根据能量值动态地进行任务的规划.

2 能量管理与任务规划

2.1 指数加权移动平均值算法

指数加权移动平均(Exponentially Weighted Moving Average， EWMA)， 是一种常用的序列数据处理方式.

EWMA主要是据前一时刻实际的观测值来求取t时刻的估计值. EWMA是以几何递减的顺序对样本进行加权， 以使最近的样本加权最高， 而最远的样本贡献很少.

EWMA(t)=αH(t)+(1-α)EWMA(t-1),

t=1,2,…,n,(14)

式中：EWMA(t)是t时刻的估计值；H(t)是t时刻的测量值；n是所观察的总的时间；α(0<α<1)表示历史测量值的权重系数. 之所以称之为指数加权， 是因为加权系数α是以指数式递减的， 即各指数随着时间而指数式递减.

在WISP中利用指数加权移动平均值算法， 首先建立关于时间的函数， 主要是从两个角度考虑： ① 充电时间过短； ② 充电时间过长. 建立的函数为

Twasted(V0)=P(fail|V0)t1+(1-P(fail|V0))t2,(15)

`式中：P(fail|V0)为任务失败的概率；t1为任务失败到重新充到起始电压的时间；t2为过度充电的时间. 且

T1=pf×t1,(16)

T2=pf×t2.(17)

通过指数加权移动平均值算法可以得到

(18)

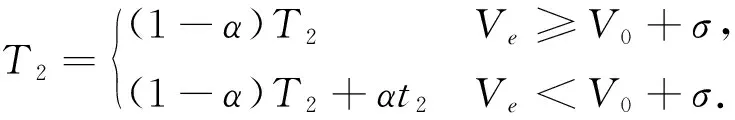
通过α与时间进行关联来找到t时刻最佳的充电时间， 并且根据式(21)来动态地调整下一时刻的时间.

(20)

通过能量模型以及指数加权平均值算法可以实时调整不同位置下标签的充电时间， 实现最佳的醒睡机制.

2.2 GSME任务同步规划算法

假设可充电无线网络n个标签， 集合为S={s1，s2，s3，…，sn}. 每个设备都有一定数量要发送的数据. 阅读器R放置在该传感器网络中给定位置L处以收集从该充电器获得能量的所有标签的数据分组. 该模型可以准确表示的常见应用场景是仓库中的监控系统， 其中RFID读取器正在从库存仓库中的多个RFID天线收集数据包， 而这些RFID任务在不向读卡器传送数据包时， 会同时从读卡器收集能量.

微型设备不需要彼此通信或同步. 这是因为在考虑能量问题的情况下， 阅读器作为集中决策者， 并根据阅读器从设备收集的相关信息决定何时收集哪些设备的数据包. 为了收集数据包， 阅读器需要知道存储在每个设备上的能量值， 根据设备的能量状态确定设备是否已经收获足够的能量来将数据分组传送到阅读器.

为了实现该目的， 阅读器可以通过执行以下三个步骤来跟踪每个设备的所需能量信息：

1) 根据RSS值以及建立的坐标系来精确确定标签的位置

RSSI=-(A+10nlog10d).(21)

2) 基于位置信息计算设备和阅读器之间的距离， 然后根据式计算每个设备随时间收获能量值.

3) 当设备向阅读器发送分组时， 可以根据该设备收集的能量减去消耗的能量来计算该设备中剩余的能量值用于传输数据包.

假设有m个标签，n个任务， 标签集合为S={S1,S2,S3,…,Sn}， 任务集合为T={T1,T2,T3,…,Tn}. 每个任务Ti需要消耗的能量为ei.

定义1p是已经分配的任务集，R是在贪婪下不能分配的剩余任务集；

定义2ci为目前标签Si中的剩余能量，gi为任务完成之后剩余能量值.

本文算法是对贪婪算法的改进. 在贪婪算法的基础上， 通过如下三个步骤来实现本文算法.

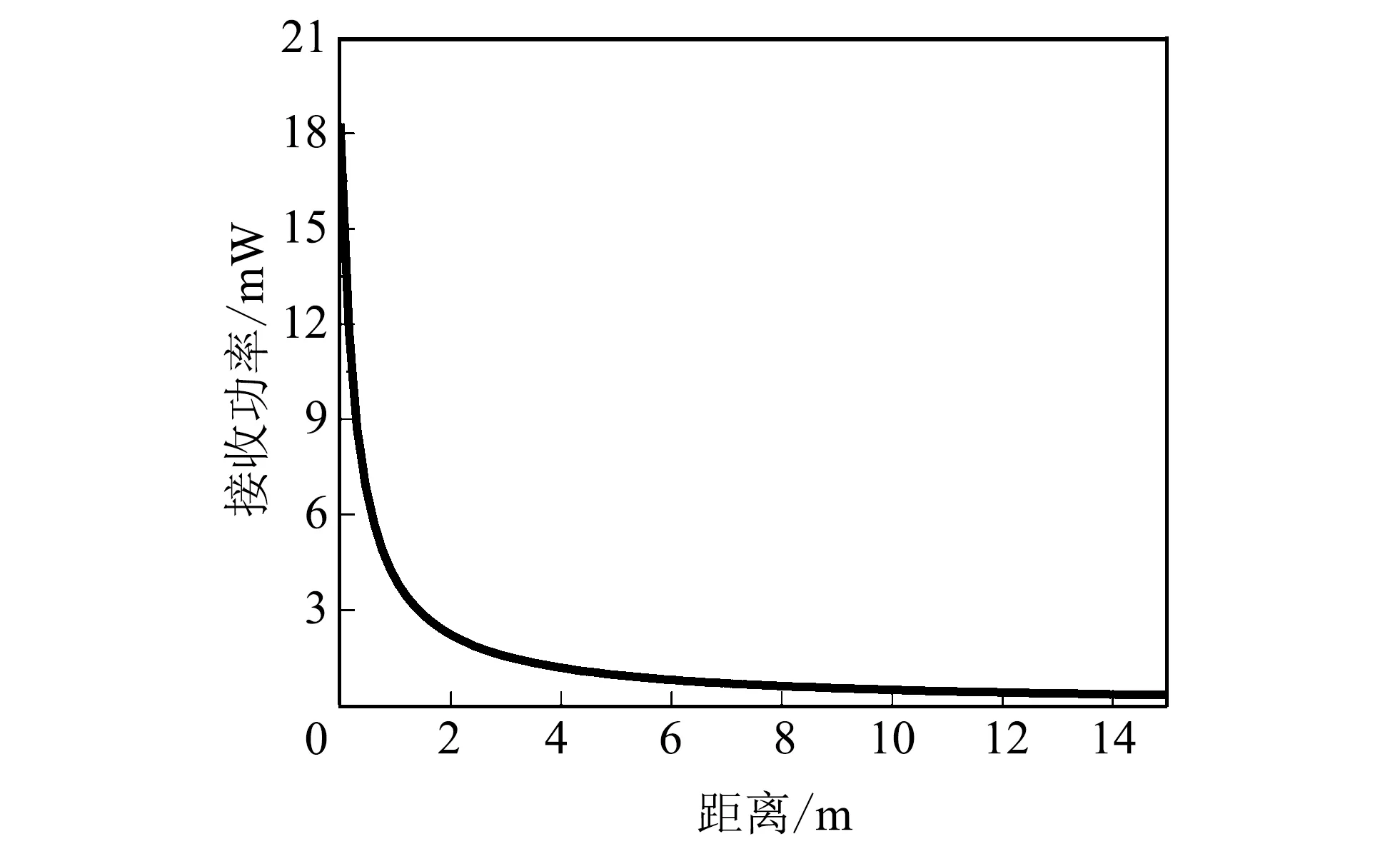
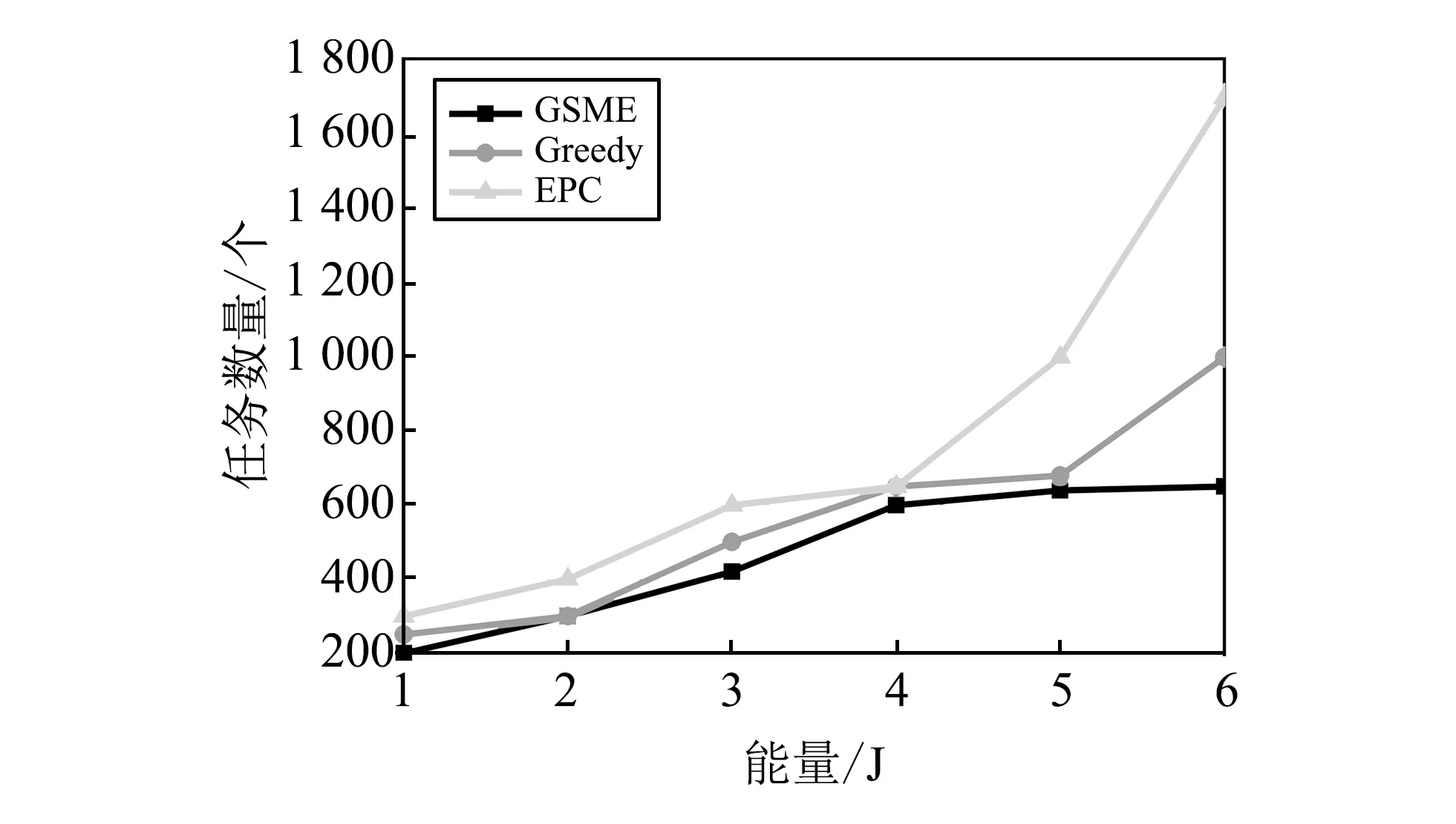
1) 任务切换. 贪婪算法是根据任务所需能量值进行排序， 按照大小顺序执行， 在此算法上进行第一步任务切换， 主要是： 对于任务Ti(Ti∈R), 在p集合中找到最小的k值， 使得ei

2) 任务移动. 任务移动阶段主要是： 对于标签Si在p集合中找到最小值k， 使得ci>ek,ci

3) 任务交换. 如果Tj(Tj∈R)可以被分配到gi或者gk中， 则对于任务Ti(Ti∈p)， 将Ti与Tk进行交换. 最终达到所有任务都被执行而且能量利用率最高.

3 实验与评价

实验硬件包括一个Impinj阅读器R420， 可以连接四根天线， 工作频率为920～925 MHz UHF频带， 多个WISP标签， 系统运行在Windows 7系统的计算机.

3.1 能量模型参数的选取

在能量模型中， 主要是参数η，α的确定， 在实验中， 要先将传感器模块关闭. 实验环境在空旷的实验室中进行. 从式(1)中可以看出功率与距离相关， 因此实验主要是改变WISP与阅读器之间的距离， 通过监测储能电容两端的电压来得到功率与距离之间的关系， 从而确定η与α的值. 使用的实验设备如图 1 所示.

图 1 实验设备Fig.1 Experimental equipment

在实验中， WISP与阅读器之间的距从0 m开始到4 m每隔0.2 m为一个定点， 每个定点实验重复10次， 测量计算出平均功率， 取其平均值. 最后将实验数据利用MATLAB进行分析处理， 最终求出η=0.301，α=0.063， 将参数代入式(2)得到WISP的能量收集模型， 如图 2 所示.

图 2 WISP的能量收集模型Fig.2 WISP energy collection model

图 2 主要是针对WISP进行的能量收集模型， 通过实验对原有的模型进行了修正， 可以更加准确地获得确定距离下标签的功率值. 从而得知某时刻确定位置下的能量值. 为下文的算法奠定基础.

3.2 指数加权移动平均值算法的仿真结果与分析

在WISP中执行的任务主要有三种： 感知、 计算、 数据传输. 利用WISP三轴加速度传感器来进行数据的感知； 之后将收集到的数据进行计算， 主要是将收集到的模拟信号利用MSP430转化为数字信号； 最终传输给阅读器， 此过程为通信. 实验主要是比较了WISP标签原有的EPC协议中的算法与本文算法.

实验中选取了3组标签， 每组标签有5个， 分别放置在距离阅读器1, 1.5, 2, 2.5, 3, 3.5, 4 m处， 利用WISP自身携带的三轴加速度传感器进行实验， 分别进行了1 000, 3 000, 5 000次感知任务、 计算任务与通信任务.

根据实验步骤， 将本文算法与WISP固有的EPC协议从执行平均时间、 平均能耗以及通信的可靠性三方面做了对比， 对比结果如图 3 所示.

从图 3 中可以看出， WISP在执行任务的时候， 相同的距离情况下， 本文所提出的EWMA算法比WISP本身EPC规定的算法所执行的时间要少； 随着距离的增大， 执行时间越来越长， 这是因为当WISP离阅读器越远， 获取能量的速度就越低， 这样执行相同的任务所需要的时间也越多. 总体来看， 本文算法比WISP传统算法用时少了15%， 提高了效率.

图 3 WISP平均执行时间变化图Fig.3 The graph of WISP average execution time change

图 4 平均能耗对比图Fig.4 Average energy consumption comparison chart

图 4 为WISP执行相同的三种任务时， 用本文EWMA算法与EPC的平均能耗图， 从图中可以看出， 无论是感知、 计算还是通信， 本文算法要比EPC所消耗的能量少近1/2. 验证了本文算法的有效性.

图 5 可靠性结果图Fig.5 Reliability result chart

从图 5 中可以看出， 在相同的距离下， 本文算法的可靠性较高， 最高达88%， 而且随着距离的增大， 不会有大幅度的降低， 有较强的鲁棒性.

3.3 GSME任务同步规划算法的仿真结果与分析

GSME任务同步规划算法主要实现在执行相同任务下消耗的能量最少， 并且执行完任务之后每个标签的剩余能量也越少， 即提高了能量的利用率. 为了验证本文算法， 实验中在距离为1， 2， 3， 4 m处分别放置三组标签， 每组各有100个标签， 一组标签执行贪婪算法， 一组标签执行GSME算法， 另一组执行WISP的EPC协议， 进行比较. 主要测试在执行相同任务的条件下能量的消耗以及在相同平均能量条件下执行的任务数量.

首先， 找到标签的时间-能量模型图， 可以实时了解标签中的剩余能量. 如图6所示.

图 6 标签的能量-时间模型Fig.6 Energy-time model of tags

1) 任务个数相同时的实验结果分析

当任务为2 500～5 000时， 三种算法在WISP中进行实现， 得到实现结果如图 7 所示， 可以看出， 在执行相同任务的情况下改进的贪婪算法即GSME算法消耗的能量最小， 贪婪算法次之， EPC算法消耗的能量最多. 且可以看出本文算法的能量消耗较EPC的消耗减少了 33.55%， 较贪婪算法提高了27.3%. 大大减少了能量消耗， 提高了能量利用率. 实验结果验证了本文算法的有效性.

图 7 执行相同任务时的能量消耗Fig.7 Energy consumption when performing the same task

2) 消耗相同能量时的实验结果分析

当消耗能量为1～6 J时， 三种算法在WISP中进行， 得到结果如图 8 所示， 可以看出， 在消耗相同能量的情况下， GSME算法所执行的任务最多， 贪婪算法次之， EPC执行的任务数量最少. 通过实验的结果可以验证本文算法的有效性.

图 8 消耗相同能量时执行任务的数量Fig.8 The number of tasks performed when consuming the same amount of energy

4 结 论

本文针对可计算RFID的能量里利用率问题， 首次建立了详细的能量模型， 提出了指数加权移动平均值算法来动态地调整充电时间， 以及根据标签所处位置和执行完任务的能量利用， 提出GSME算法. 在WISP能量模型基础上， 利用可计算这一特性， 将算法在WISP中实现， 大大提高了能量的利用效率. 解决了前期必须改变硬件的难题， 在达到相同目的的条件下节省了时间与成本. 但是本文并没有考虑并行解码的问题， 当多个标签向阅读器一起发送消息时候， 阅读器的解码率会降低， 后续研究中将会解决此问题.