90°弯管流动预测评估及流动特性研究

，,,

(1.中国安全生产科学研究院，北京100012;2.中国舰船研究设计中心， 武汉 430064；3.武汉大学 水射流理论与新技术湖北省重点实验室，武汉 430072)

弯管是船舶管路系统中一种极为常见的部件，具有改变流体运动方向实现流体介质的输运的实用功能[1-2]。流体在弯管处会呈现出丰富的流动现象，管壁内侧区域会形成分离区，其截面上伴随着二次流动(迪恩涡)的发展，流动呈现出复杂的三维特性，因此，弯管流动作为一种经典流动现象，一直受到国内外研究者的广泛关注，也成为检验湍流模型预测能力的典型流动。

目前，基于CFD的弯管流动已取得一定进展[3-6]，但就湍流模型对弯管流动的预测性能评估还缺少系统研究，对弯管内迪恩涡的发展规律及机理研究尚不充分。应用6种湍流模型分别对弯管内部流动进行计算分析，以评估湍流模型对模拟结果的影响，并对弯管内的二次流动的运动规律进行分析，为后续弯管内部磨损预测的流场模拟提供较优的计算方案。

1 90°弯管模型

采用文献[7]的试验数据检验湍流模型对弯管流动的预测能力，并采用测试数据就湍流模型对磨损计算的影响进行对比分析。

试验弯管模型见图1，弯管直径D= 48 mm，曲率半径为2.8D。为了减小入口流动对模拟的影响，将弯管进口的直管段延长15D；将弯管出口的直管段延长10D，以减小出口处可能出现的回流影响从而使得计算更加稳健。定义R*=r-R，因此，当R*/D为0时表示弯管的内侧壁面，当R*/D为1时，表示外侧壁面。试验中采用的介质为纯水，入口处的雷诺数Re为43 000，试验中给出了弯管进口上游0.58D、30°截面、60°截面、75°截面，以及弯管出口下游1.0D、6.0D处的速度分布。

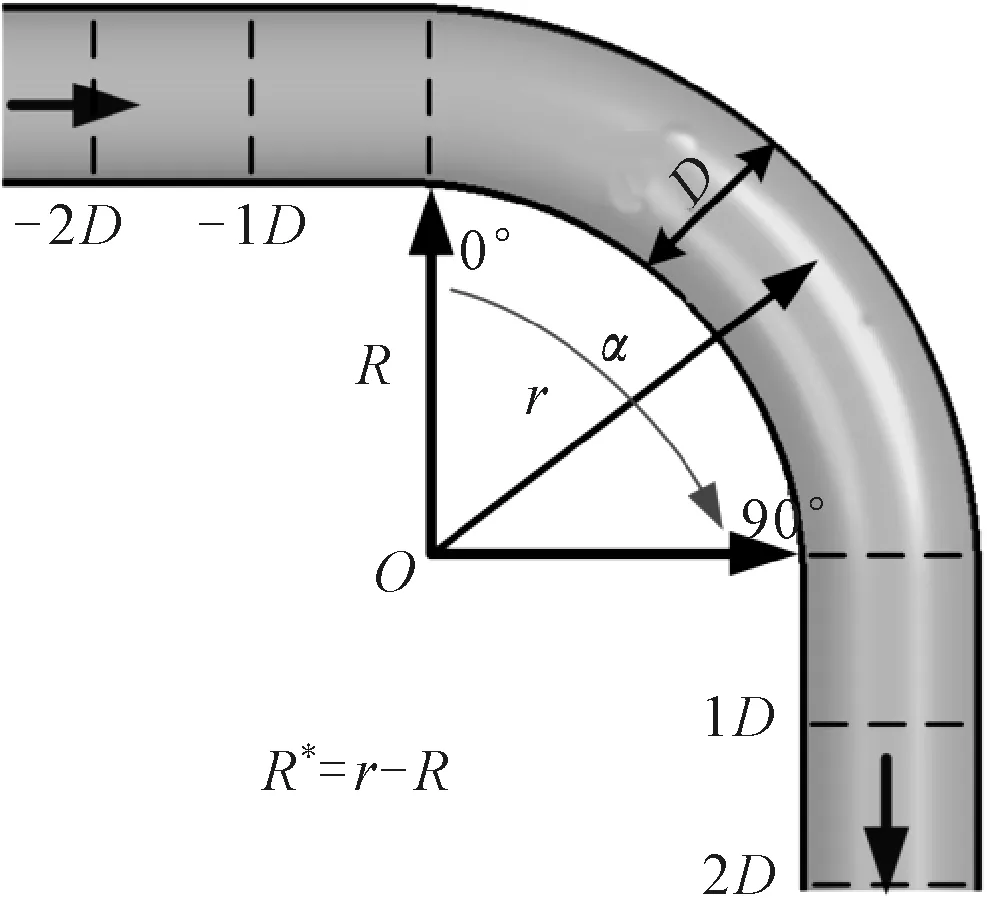
图1 90°弯管模型示意

2 数值方法

2.1 湍流模型

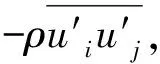
采用两种不同计算方案对比分析6种常用的RANS湍流模型对弯管内流场的预测能力。方案一具体包括标准k-ε模型(SKE)、重整化群k-ε湍流模型(RNG)和可现实k-ε湍流模型(RKE)；方案二包括LB湍流模型(LB)、AKN湍流模型(AKN)和剪切应力输运湍流模型(SSTk-ω)。方案一中的3种k-ε系列的湍流模型只适用于高雷诺数流动的情况，对于近壁区域的低雷诺数流动分子黏性的影响不能忽略，文中采用标准壁面函数法[7]。方案二中LB、AKN湍流模型建立了合适的阻尼函数，使其在近壁区域同样适用，而SST湍流模型在边界层内部采用标准k-ω模型求解，在边界层外充分发展的湍流区域，自动切换为适用于高雷诺数流动的SKE模型。

2.2 网格无关性分析

方案一的网格无关性验证采用3套网格(Mesh 1、Mesh 2和Mesh 3)，其网格节点数分别为20万、42万和88万，见图2。计算后对y+进行检验，3套网格y+的最小值为40，最大值为160，因此，满足标准壁面函数的使用条件。经对比不同截面上的速度分布，采用方案一中的3种湍流模型结合Mesh2都能给出网格独立的解。

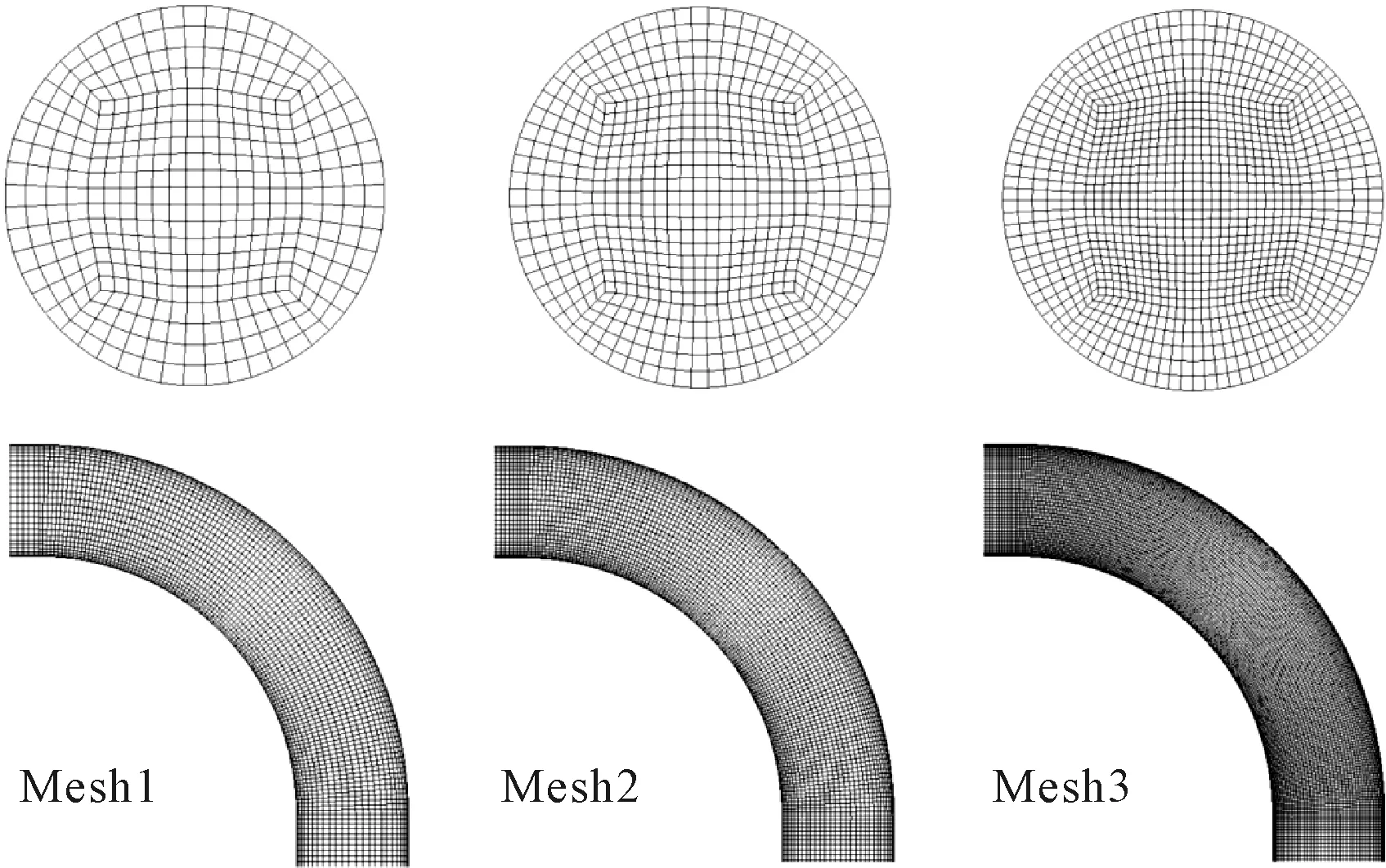
图2 方案一网格无关性分析

方案二的网格无关性分析所采用的网格具有细密的边界层网格，其网格节点数分别为80万、120万和160万，见图 3。经计算验证，当网格数量超过120万时，速度分布随着网格节点数的增加不再变化，因此，方案二采用Mesh 5这套网格的计算结果进行分析。

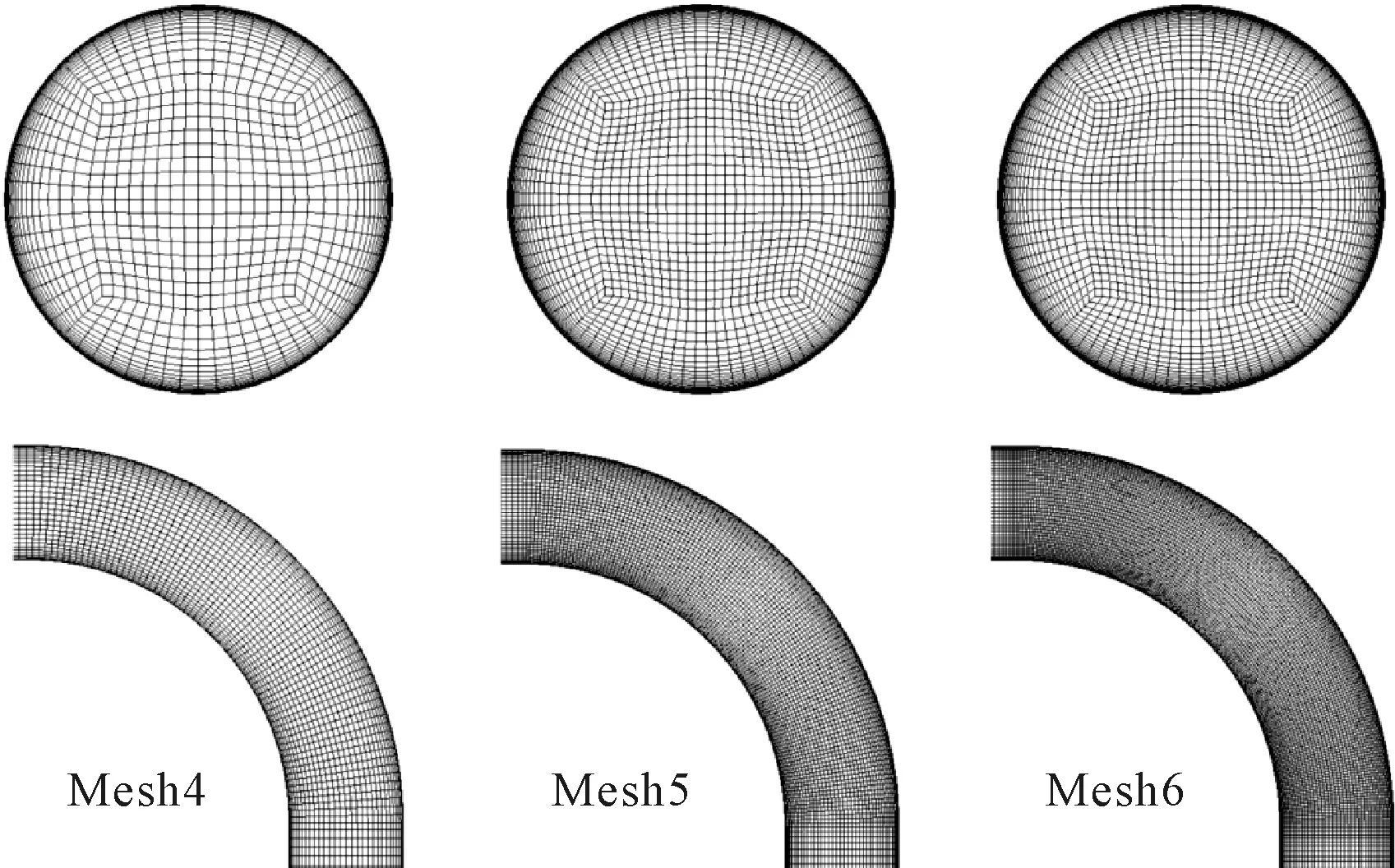
图3 方案二网格无关性分析

3 结果分析

3.1 湍流模型对弯管流动的影响分析

方案一中，SKE模型的计算结果见图4。在弯管上游0.58D处的预测结果与试验值符合较好，进入弯管后，在30°截面上的速度分布仍然能够与测量值较好的符合。在60°截面处，由于离心力的作用，外侧区域的流动呈现出加速的趋势，而内侧区域开始出现逆压梯度驱动的流体速度的扭曲分布，此处的计算值在靠近外侧区域与试验值相近，但是在靠近弯管内侧壁面附近SKE没有捕捉到速度的扭曲分布。在75°截面，内侧区域的速度分布扭曲程度降低，逆压梯度效应减弱，此时计算值开始与试验值靠近。在距离弯管出口下游6D截面处，SKE能较好地预测出管道内部的速度分布。

RNG在-0.58D和30°截面的预测值与试验值符合较好，见图5。此时RKE模型也给出了较好的预测值，见图6。但是，当流动开始在逆压梯度的作用下变得扭曲时，RNG和RKE模型的预测结果与试验值都有明显偏差。在弯管出口下游1D处，SKE、RNG和RKE都低估了管心附近的流速。在下游6D处，逆压梯度效应减弱，流动变得更加均匀，方案一中的3种湍流模型预测结果都很接近。

计算方案一中的3种高雷诺数k-ε模型都给出了相近的预测结果，在弯管出口下游1D处SKE给出的计算值与试验值最为接近。RNG模型虽然考虑了主流高湍流时均应变率的效应，但是在弯管内流的计算中并未发现优于SKE模型。RKE模型理论上在计算湍黏时考虑了旋转和曲率相关的影响，但在本算例中并未有效地捕捉到由逆压梯度引起的扭曲速度分布。

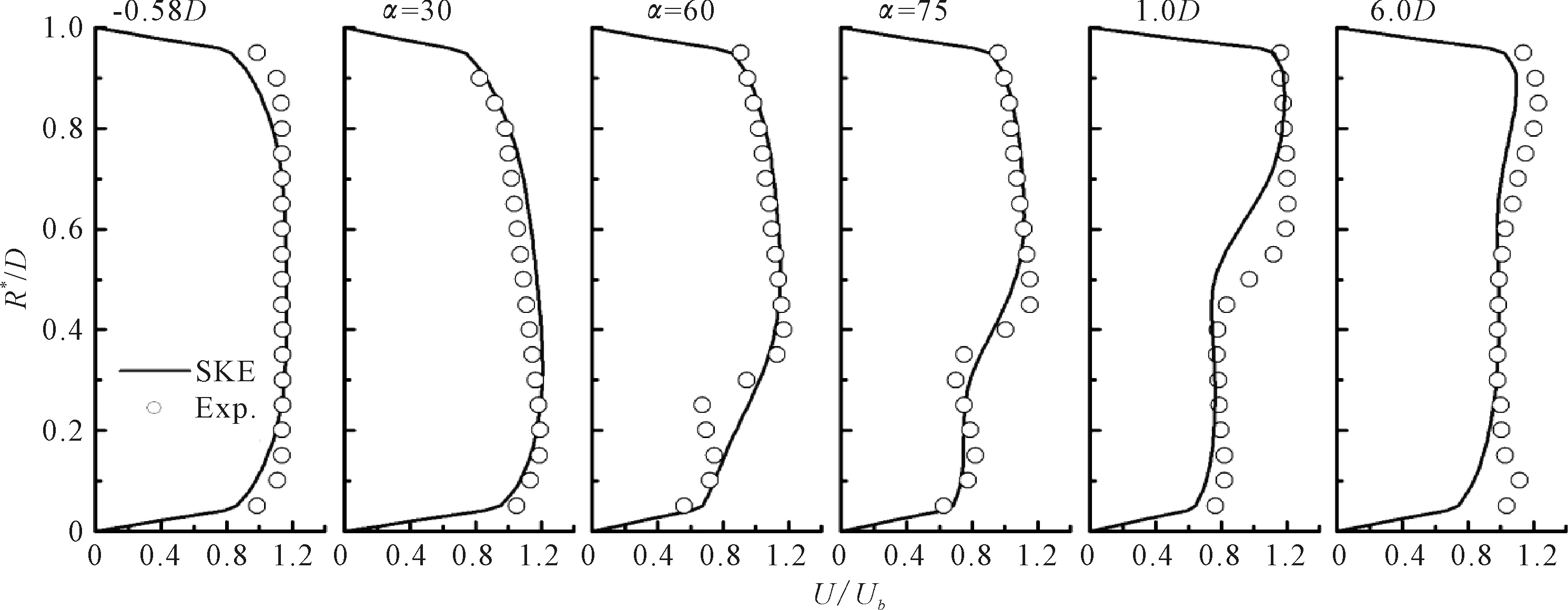
图4 SKE模型计算结果

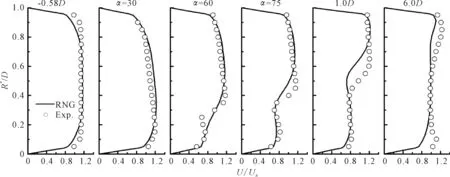
图5 RNG模型计算结果

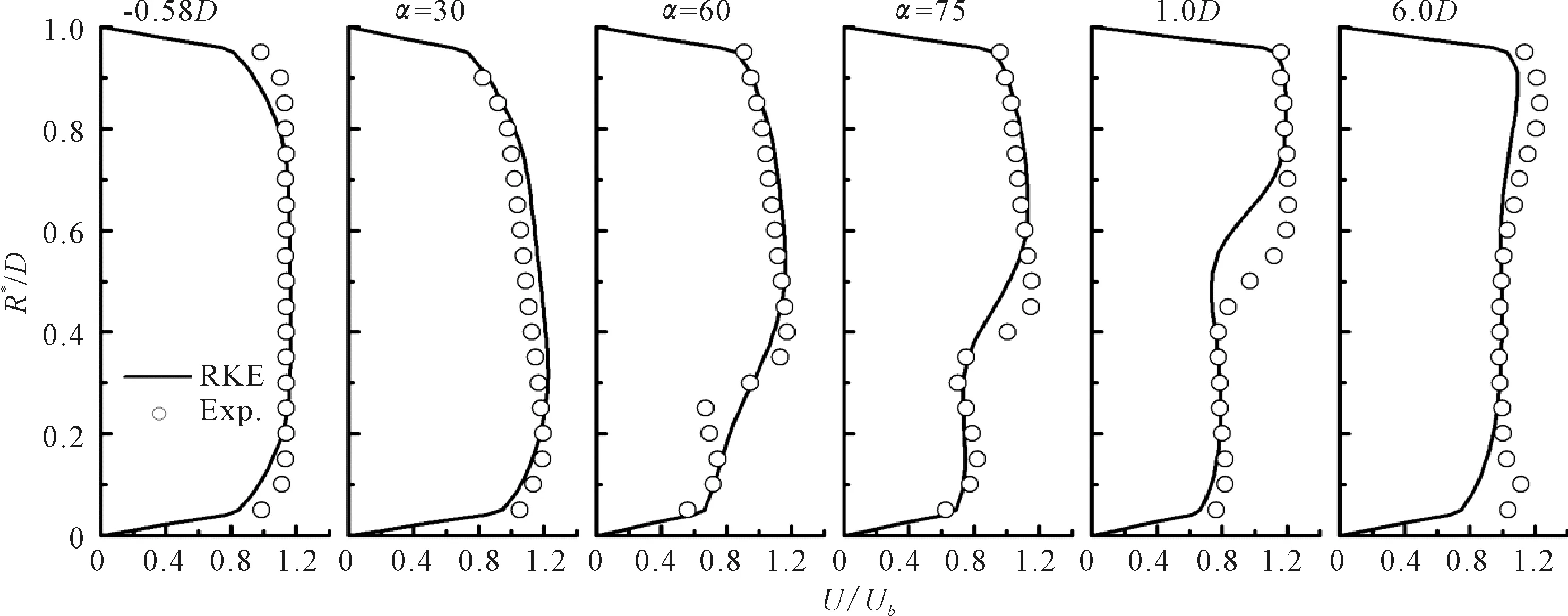
图6 RKE模型计算结果

本研究中采用高雷诺数k-ε系列的湍流模型都是配合标准壁面函数法进行壁面流动的计算处理的，这种基于局部平衡假设的壁面函数法在预测强旋流和分离流动时本身的预测能力还有待商榷，因此，不同近壁处理方式对弯管内部流动计算的影响同样值得研究。选用标准壁面函数法的出发点是将方案一作为一种经济型备选计算方案，旨在用较小的计算成本得到可靠的预测结果。方案一的计算结果表明，SKE模型配合标准壁面函数法在计算弯管内流时与RNG和RKE模型预测能力等同，同样具有一定的准确度。

方案二中LB湍流模型的计算结果与RNG和RKE模型给出的预测结果有相同趋势，在60°、75°和下游1D截面处的预测结果都与试验值有明显偏移，见图7，AKN的模拟结果也有类似规律，见图8。因此，LB和AKN两种低雷诺数湍流模型对弯管内流动的预测较高雷诺数版本的k-ε系列模型并没有明显改善。SST模型的预测结果见图9，在弯管进口上游0.58D处，其计算结果和测量值能够较好符合，在弯管区域内部的预测结果较其他5种湍流模型也与测量值最为接近。距离出口下游1D处，SST模型在内侧区域和管中心区域同样低估了流速分布。

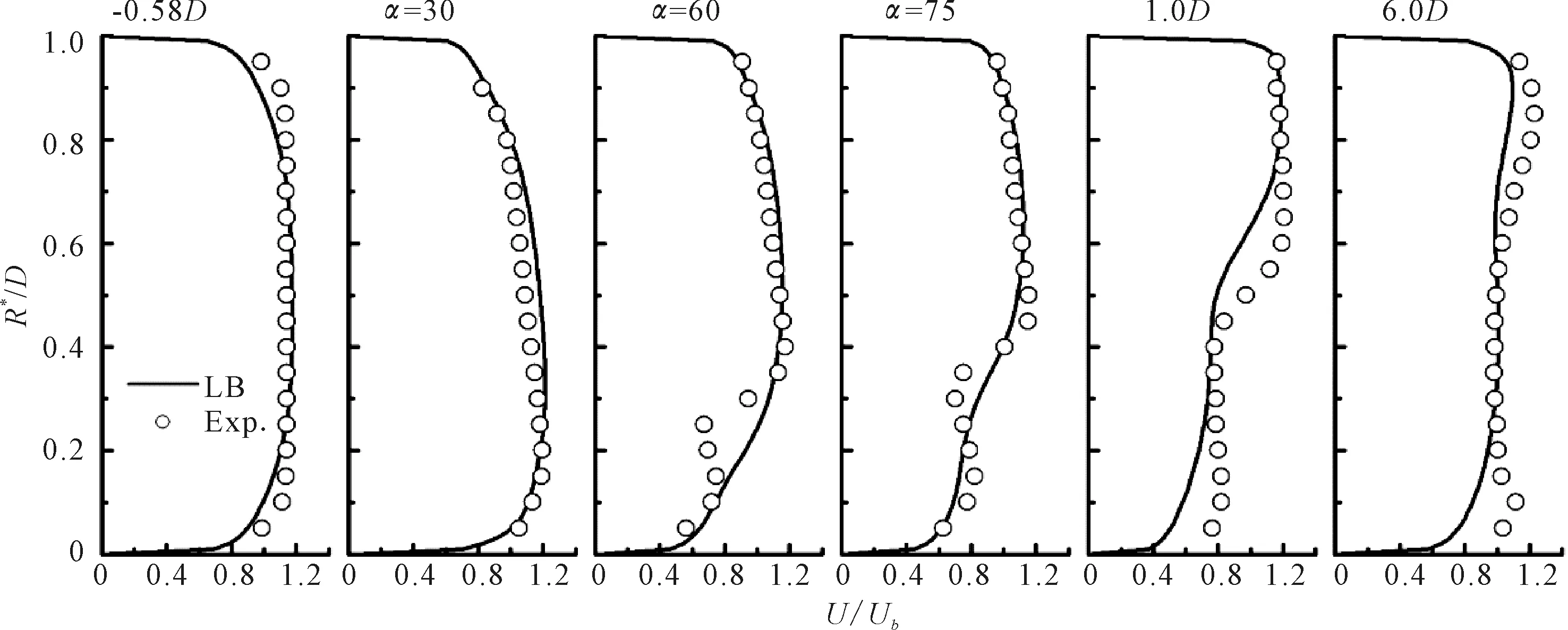
图7 LB模型计算结果

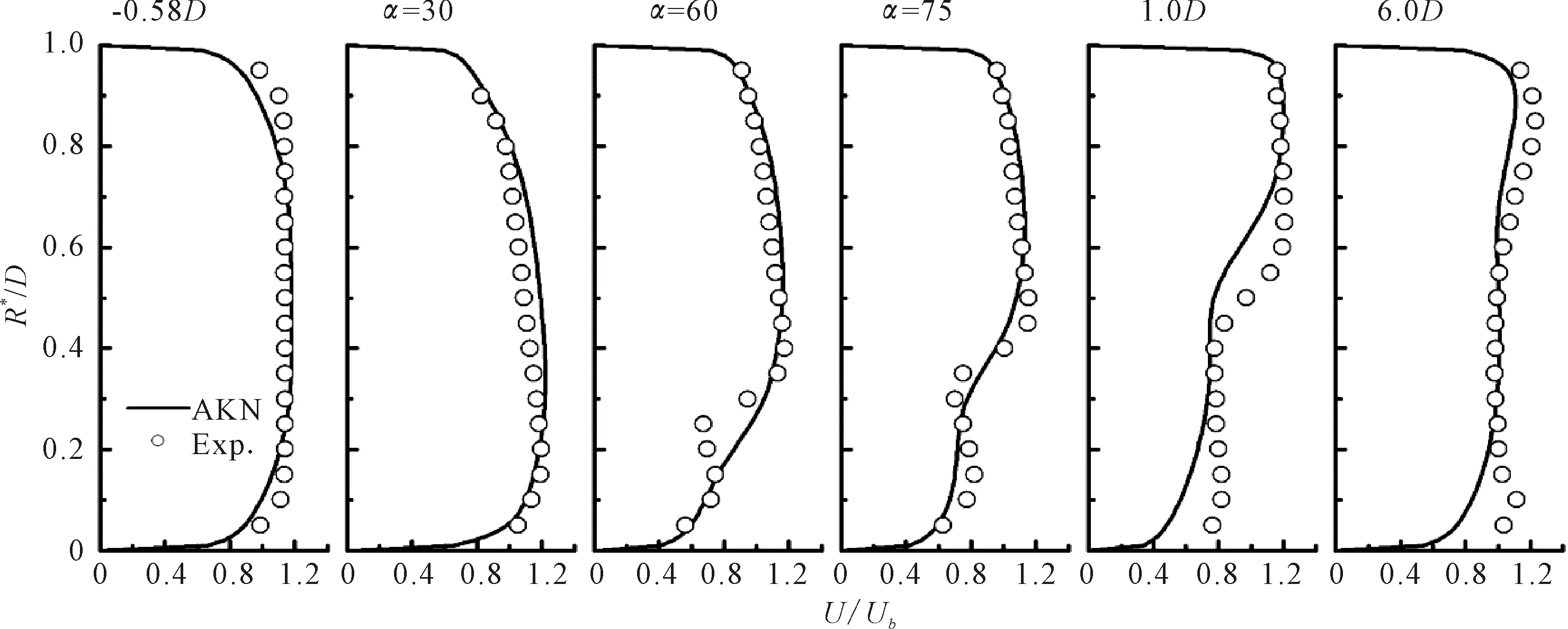
图8 AKN模型计算结果

图9 SST模型计算结果

方案二的计算结果表明，SST模型在弯管内部的流场预测最为准确，与试验测量值能够较好符合，而LB和AKN两种低雷诺数模型与方案一中的高雷诺数k-ε系列模型相比，其预测能力未见明显改善。

3.2 迪恩涡发展规律分析

流体通过弯管时，由于受到离心力的作用，会在截面上产生一对反向运动的对称旋涡，即迪恩涡。基于前述分析，将采用SST模型的模拟结果对迪恩涡的发展规律进行分析，旨在为磨损预测的结果分析奠定理论基础。

弯管不同截面处速度云图和矢量分布见图10。在0°位置，即为弯管部分的进口位置，速度分布比较均匀，速度核心区域略微偏向弯管内侧，此时截面上没有明显的二次流动。在15°和30°的位置，截面上的二次流动初步形成，此时速度核心区域靠近内侧壁面。在45°截面靠近弯管内侧壁面位置的底部，开始出现一个低速区域，此时速度核心区域没有继续向内侧发展。随着角度的增大，弯管内侧底部的低速区域逐渐发展，外侧区域的流体开始加速。由矢量图可以看出，随着角度的增大，在离心力的作用下，二次流动不断发展，弯管外侧流体的速度开始增加，流体从弯管左右两侧由外向内沿着壁面附近进行二次流动，在内侧壁面汇合之后朝向圆管中心发展。

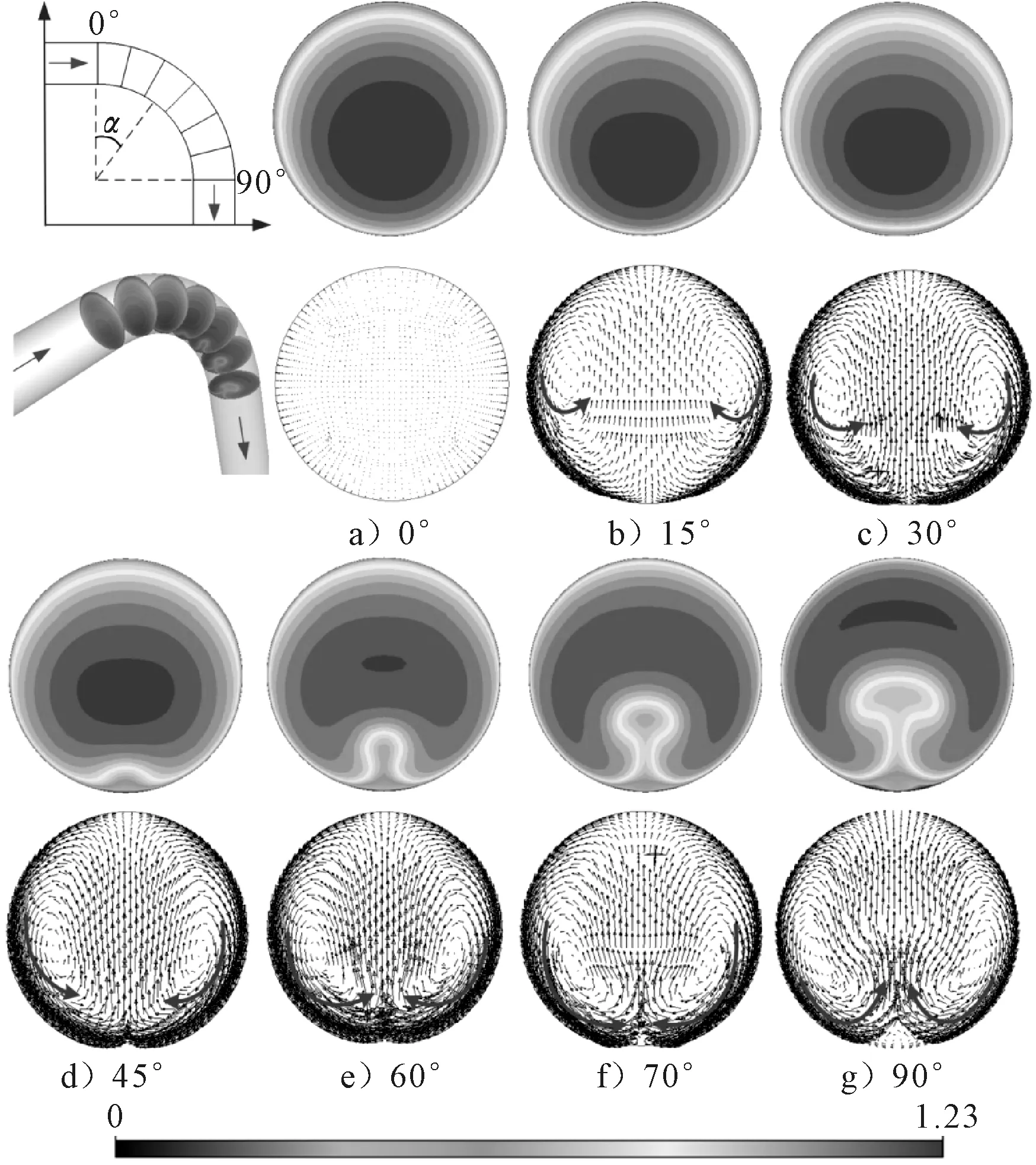
图10 弯管不同角度截面速度分布

流体经过弯管后在下游直管段的速度分布见图11。从0.5D到2D的4个截面可以发现，靠近圆管中心的低速区域十分明显，此时迪恩涡中心逐渐向圆管中心区域靠近。在所取的3D到6D之间的4个截面，圆管中心的低速区逐渐消失，速度开始趋于均匀，二次流动逐渐减弱。

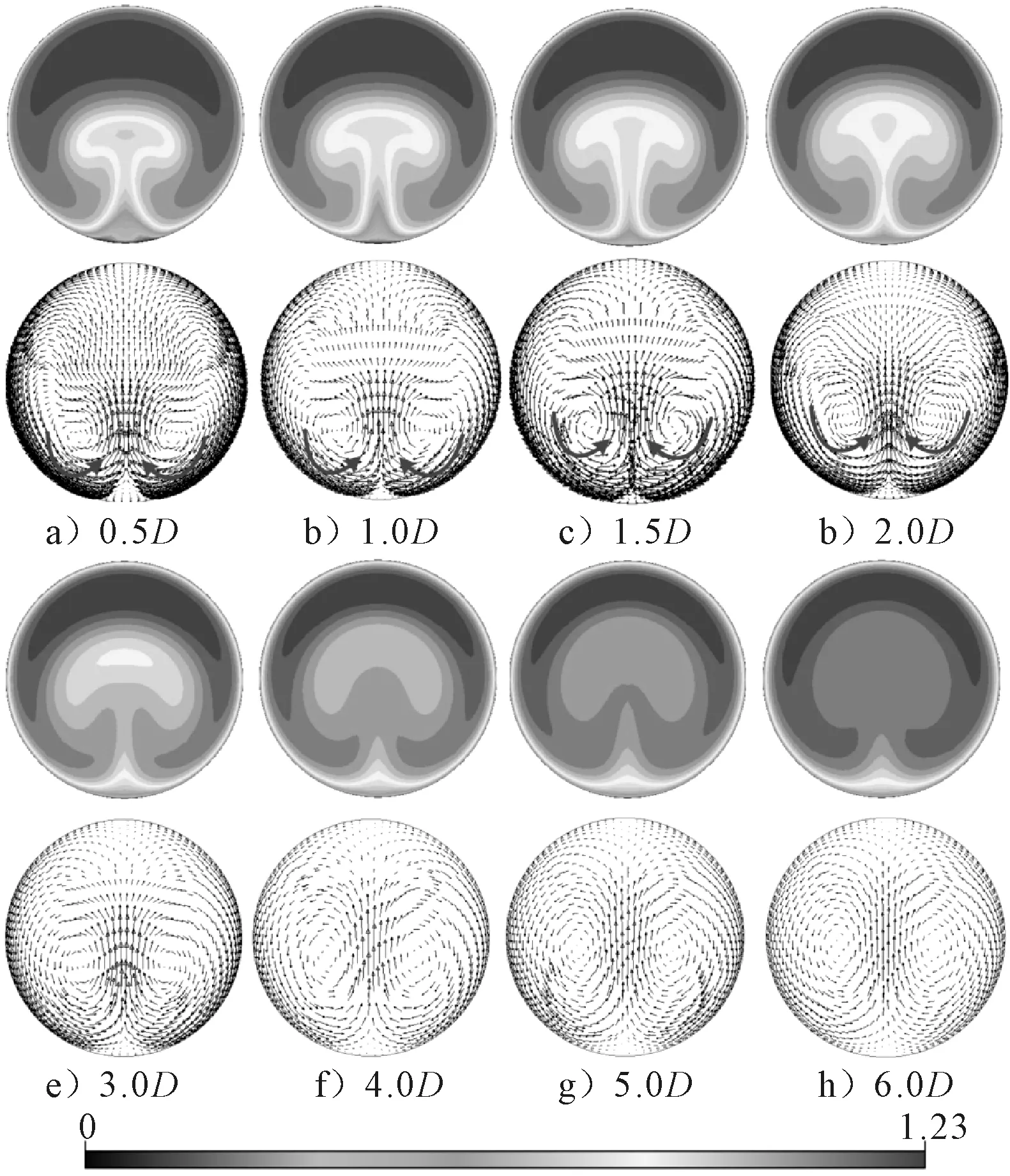
图11 弯管出口下游不同截面速度分布

为了更清楚地研究二次流动的发展规律，引入一个二次相对动能参数K，其表达式为

(1)

式中：v、w为截面上二次流动的速度；Ub为进口流速。因此，K越大，表示截面上的二次流动越明显。

弯管出口下游不同截面处二次相对动能分布情况见图12。

图12 不同截面二次相对动能分布

在弯管出口位置0D处，弯管左右壁面靠近内侧部分的二次流动较大，靠近内侧的中心位置也有一个较大二次流动区域，此处二次流动较强的区域呈现出W形分布。在0.5D位置，壁面附近二次流动区域开始变厚，中心区域的二次动能强度明显减小，二次能动区域分布分离为3块，W形分布消失。这种分布规律一直保持到1D和1.5D处的截面。在2D位置，壁面附近较大的二次动能区域几乎消失，但是中心的高速区域仍然存在。在随后的位置，中心区域的较大二次动能分布逐渐向圆管中心移动，同时在其两侧出现两个对称的二次流动滞止区域。

4 结论

1)采用6种湍流模型分为两种不同的流动预测方案对弯管内部的流场进行模拟计算，针对不同湍流模型对弯管内部流动的预测能力进行对比分析。结果表明，方案一中SKE模型配合壁面函数法和RNG以及RKE湍流模型的预测能力类似，都能大致预测出管内流动的分布规律，但对弯管内侧区域速度扭曲的计算结果与试验值存在明显差异；方案二中的两种低雷诺湍流模型较高雷诺数k-ε湍流模型的预测能力并未显著提高，而SST湍流模型给出的计算结果与试验值最为符合。

2)基于SST模型的计算结果对迪恩涡的发展规律进行了研究。分析表明，在弯管内部随着角度的不断增加，二次流动不断增强，截面上外侧流体沿着两侧壁面流向弯管内侧，在底部汇合后又向管心流动，迪恩涡的中心由外侧不断向内侧靠近；在弯管出口的下游截面，迪恩涡开始耗散，中心区域的低速区域开始消失，壁面区域较大的二次动能区域逐渐消失，中心区域的主二次动能区伴随着两个对称的二次动能滞止区不断靠近圆管中心，整个过程迪恩涡的中心由内侧向中心不断移动，整个流场的分布逐渐变得均匀。