函数的奇偶性在高中数学解题中的运用

王月娉

[摘   要]奇偶性是函数的一个很重要的性质.在解数学题时，如果能够准确运用函数的奇偶性，很多问题都能迎刃而解.研究利用函数奇偶性解决问题的方法，对提高学生解题能力有很大的帮助.

[关键词]函数;奇偶性;运用

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）35-0019-02

奇偶性是函数的一个很重要的性质.利用函数的奇偶性解题的方法，课本没有专门的介绍，学生学习起来有一定的难度.学生虽然掌握了判断函数奇偶性的方法，但是利用函数的奇偶性解题时仍会出现错误.因此有必要进一步研究其性质的运用.

函数的奇偶性有很多重要的结论.比如：

（1）一个函数是奇函数或者偶函数，其定义域关于原点对称;如果一个函数的定义域关于原点不对称，那么它是非奇非偶函数.

（2）若奇函数[f（x）]在[x=0]处有定义，则必有[f（0）=0] .

（3）若函数[f（x）]是奇函数，则[f（x）max+f（x）min=0] .

（4）奇函数的图像关于坐标原点对称，偶函数的图像关于[y]轴对称.反之也成立.

（5）奇函数在关于坐标原点对称的区间上的单调性相同;偶函数在关于坐标原点对称的区间上的单调性相反.

下面通过具体实例来介绍函数的奇偶性在解題中的运用.

【类型一】正确把握定义

函数具有奇偶性，它的定义域一定关于原点对称.所以在解题时一定要把握好这一知识点.

[例1]已知[f（x）=ax2+bx]是定义在[[a-1 ，2a]]上的偶函数，那么[a+b=]（）.

A. [-13] B. [13] C. [12] D. [-12]

解： 依题意可知，区间[[a-1 ，2a]]是关于原点对称的，则[（a-1）+2a=0]， 所以[a=13] .

又函数[f（x）]是偶函数，所以[f（-x）=f（x）]，即[ax2-bx=ax2+bx]对定义区间上的任意[x]恒成立，所以[b=0]，所以[a+b=13] .

【类型二】求函数解析式

求函数的解析式的方法很多，如果涉及奇偶性，我们一定要抓住“对称”这一特点.

[例2]已知函数[f（x）]是定义在[R]上的奇函数，且当[x>0]时， [f（x）=x2-x]，则函数[f（x）] 的解析式是             .

解：因为函数[f（x）]是定义在[R]上的奇函数，所以[f（0）=0].

当[x<0]时，[-x>0]，

所以[f（-x）=（-x）2-（-x）=x2+x].

又[f（-x）=-f（x）]，所以[f（x）=-f（-x）=-x2-x].

综上可得  [f（x）=x2-x ， x>00  ，       x=0-x2-x，x<0]  .

【类型三】函数求值

求函数值题型，方法众多.如果题目给出函数的奇偶性，那么我们就要充分利用它的性质解题.这样我们就可以避免复杂的运算，达到快速解题的目的.

[例3]已知函数[f（x）]是定义在[R]上的奇函数，当[x<0]时，[f（x）=2x3+x2]，则[f（2）=]                     .

解法一：由题设可知，对任意[x∈R]，有[f（-x）=] [-f（x）]，即[f（x）=-f（-x）]，所以[f（2）=-f（-2）=12] .

解法二：当[x>0]时，[-x<0]，则[f（-x）=2（-x）3+]   [（-x）2=-2x3+x2].

又[f（-x）=-f（x）]，所以 [f（x）=-f（-x）=2x3-x2]，

即当[x>0]时， [f（x）=2x3-x2]，所以  [f（2）=12] .

[例4]已知[y=f（x）] 是奇函数，当[x<0]时，[f（x）=x2+ax]，且[f（3）=6]，则[a]的值为（）.

A. [5]B. [1]C. [-1]D. [-3]

解法一：因为[y=f（x）]是奇函数，且[f（3）=6]，所以[f（-3）=-6]，则[9-3a=-6]，解得[a=5]，  选A .

解法二：当[x>0]时，[-x<0]，则[f（-x）=x2-ax] ，又 [f（-x）=-f（x）]，

所以[f（x）=-f（-x）=-x2+ax]，

即当[x>0]时， [f（x）=-x2+ax]，

由 [f（3）=6]得[-9+3a=6]，  解得[a=5]，  选A .

【类型四】图像的应用

函数的图像能够直观地体现函数的性质.因此，解题时如果依据题设条件作出它的简图，借助图像寻求解题思路，或者直接得到答案，能够收到事半功倍的效果.

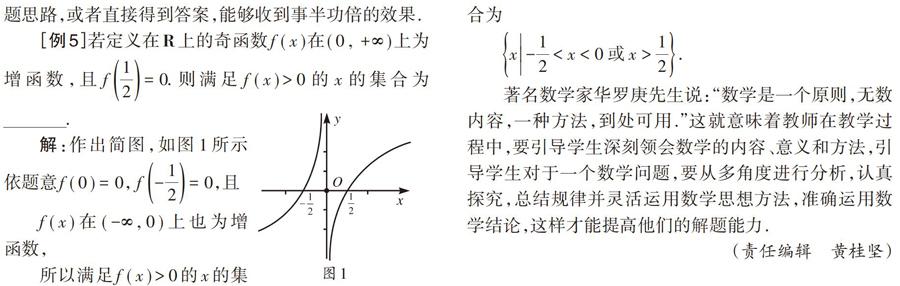
[例5]若定义在[R]上的奇函数[f（x）]在[（0 ， +∞）]上为增函数，且[f12=0].则满足[f（x）>0]的[x]的集合为               .

解：作出简图，如图1所示依题意[f（0）=0]， [f-12=0]，且

[f（x）]在[（-∞ ， 0）]上也为增函数，

所以满足[f（x）>0]的[x]的集合为

[x-1212] .

著名数学家华罗庚先生说：“数学是一个原则，无数内容，一种方法，到处可用.”这就意味着教师在教学过程中，要引导学生深刻领会数学的内容、意义和方法，引导学生对于一个数学问题，要从多角度进行分析，认真探究，总结规律并灵活运用数学思想方法，准确运用数学结论，这样才能提高他们的解题能力.

（责任编辑 黄桂坚）