目标引导系统模型研究

周斌斌，马骊群，赵子越

(航空工业北京长城计量测试技术研究所，北京 100095)

0 引言

大尺寸测量在航空航天、船舶、高铁等大型制造领域中占有举足轻重的地位[1]。激光跟踪仪是一种带有合作靶标的高精度测量设备，其数字化水平直接影响了大尺寸测量的数字化水平[2]，能够很好的在不同环境下解决各种测量问题[3]。但激光跟踪仪在大尺寸测量过程存在如下问题：①不能像三坐标机一样实现自动化测量，使用时需要手持反射镜定位到目标点；②在高空环境测量时，靶球的放置难度高，危险系数大，不利于人工操作；③在大批量相同样件的测量中，工作的重复性大，人工测量的效率低下。为了解决以上问题，对于目标模型已知的情况，采用机械臂及加持机构来引导靶球抵达目标点，从而实现目标的自动定位[4-7]。

在使用机械臂夹持靶球引导到目标点的过程中，需要获取机械臂末端执行器的位姿和被测目标点的位姿[8]。因此，本文先介绍和分析空间刚体位置和姿态的描述方法[9]，然后利用这些方法对激光跟踪仪、机械臂、被测目标点建模。最后使用Matlab仿真，验证方案的可行性[10]。

1 描述空间刚体位置和姿态的基本方法

对机械臂、激光跟踪仪等进行目标定位时，需要获取机械臂、激光跟踪仪、模型被测点的位置和姿态。坐标系中的位置参数使用(x,y,z) 来描述，常见的姿态表达方式有：正交旋转矩阵法、三角度表示法、双向量法、单位四元数法[9]。

1.1 单位四元数法

坐标系的任何旋转都可表示为绕特定轴旋转特定角度，因此坐标的旋转可以用单位四元数表示，将其记作一个标量加上一个向量

(1)

(2)

在使用单位四元数法时，需要已知特定轴和特定角度的数据，如果刚体的位姿在随时改变，则无法使用此方法表示。

1.2 三角度表示法

三角度表示法是根据绕三个轴依次的旋转的角度描述目标姿态的方法。由于不能绕同一个轴线连续旋转两次，因此根据旋转顺序的不同，分为两种不同的表达方式：欧拉式和卡尔丹式。目前广泛使用的旋转角顺序为roll-pitch-yaw，即

R=Rx(θr)Ry(θp)Rz(θy)

(3)

该表示方法在描述船舶、飞机和车辆的位姿时十分直观。roll,pitch,yaw分别表示绕x,y,z轴的旋转。但是，三角度表示法的缺点是存在奇异点，该问题会导致无法正确的描述目标姿态。

1.3 双向量表示法

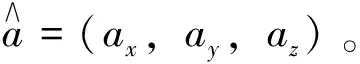
(4)

对于机械臂的末端执行器，定义接近向量比定义欧拉角或横滚-俯仰-偏航角更方便。因此，本文采用双向量法描述机械臂末端执行器的位姿。

1.4 正交旋转矩阵法

正交旋转矩阵法使用参考坐标系的坐标轴单位向量来描述目标的姿态。对于三维坐标系，每一个单位向量有3个元素，它们组成了3×3阶正交矩阵ARB

(5)

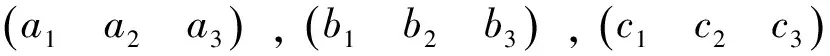
1.5 平移和旋转的组合

为了表示两个坐标系之间位置变换和旋转变换的组合，常使用齐次变换矩阵，其表达方式如式(6)所示。

(6)

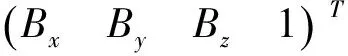
为了保证建模的准确性与高效性，本文中刚体的姿态采用双向量表示法和正交旋转矩阵法描述，而最终的位姿统一使用齐次变换矩阵方法描述。

2 目标引导模型的建立

机械臂夹持靶球放置到目标点的过程中，整个目标引导系统中必须存在激光跟踪仪、机械臂及夹持机构和模型已知的被测目标。激光跟踪仪作为测量设备，建立测量坐标系。机械臂作为执行机构，需要在已知机械臂的基坐标和各个轴角度的情况下求解出末端轴的坐标系。角耦目标反射镜作为被抓取的机构，需要通过控制机械臂的6个角度调节靶球的位姿。被测目标点的理论位置和姿态在设计图纸中已经给出。通过坐标系的转换，实现靶球和被测点的位姿统一，使测量系统中的所有坐标系转换到激光跟踪仪的测量坐标系中[11]。目标引导系统组成及关联如图1所示。

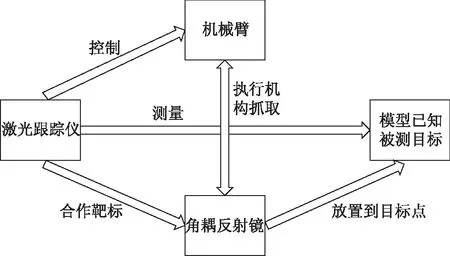
图1 目标引导系统组成及关联

角耦目标反射镜是激光跟踪仪的合作靶标，机械臂通过执行机构携带角耦目标反射镜并将其放置到目标点，之后激光跟踪仪即可测量被测目标。在整个自动引导测量系统中，激光跟踪仪占据主导地位，它所建立的坐标系为基坐标系，其它坐标系需要转换到基坐标系中。机械臂的任务是改变携带反射镜的执行机构的位置和姿态，从而改变角耦目标反射镜的位姿。

通过以上分析可知，在整个过程中需要建立激光跟踪仪、机械臂和被测目标的模型。

2.1 激光跟踪仪模型的建立

激光跟踪仪作为工业测量中常用的设备，能够实现对目标的自动跟踪和测量，具备测量精度高、测量方法简单等优点，适用于大尺寸工件配装测量[2-3]。激光跟踪仪由跟踪仪头、控制器、用户计算机、目标角耦反射镜(靶镜)及测量附件(靶座、三脚架)等组成[3]，如图2所示。其测量原理如图3所示。

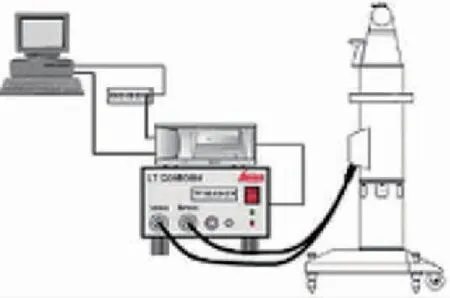
图2 激光跟踪仪的基本组成

在激光跟踪仪工作时，其测距系统测得精确距离L，其测角系统测得目标方位角α和俯仰角β。之后由测量组合(α,β,L) 经过坐标转换，获得空间三维直角坐标(X,Y,Z)。即

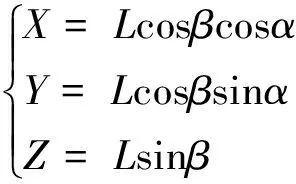
(7)

在激光跟踪仪的测量过程中，通常搭配SA软件的使用，该软件可配合激光跟踪仪建立测量坐标系。因此，以SA软件建立的测量坐标系{O0}为基坐标系，本文后面的坐标均转换到该坐标系下。

2.2 机械臂模型的建立

机械臂末端轴坐标系{O6}与基坐标系{O1}的关系可以通过齐次变换矩阵求解。由于正交旋转矩阵参数过多，故先求解机械臂的D-H参数，再求解末端轴坐标系与基坐标的关系[4]。

2.2.1机械臂D-H参数

本系统中采用的机械臂为KUKA KR60HA，适用于激光测量、部件测量等领域。该机械臂的腕轴具有极高的准确性和速度。KUKA KR60HA机械臂6个轴的旋转范围如表1所示。

表1 旋转轴的旋转范围

为了确定机械臂的D-H参数模型，还需要已知机械臂的基本尺寸参数，如图4所示。

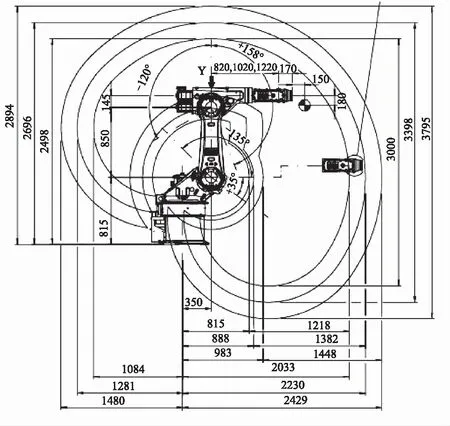
图4 KUKA机械臂的参数

根据对机械臂的旋转范围和尺寸参数的分析，可以得到D-H参数模型，如表2所示。

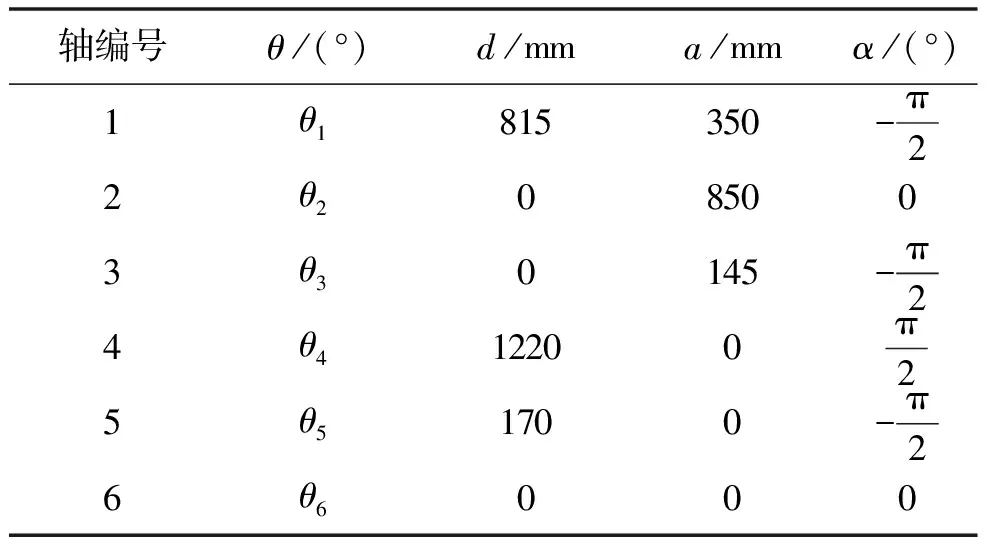
表2 KUKA KR60HA的D-H参数

需要注意的是：本文中采用的D-H参数模型，均为标准的D-H参数模型。

2.2.2机械臂正运动学模型

采用齐次变换矩阵来表示机械臂的模型。对于该6轴机械臂，根据以上求出的机械臂D-H参数，其末端轴相对于基坐标系的表达式为

(8)

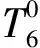
Ai=Rotz,θiTransz,diTransx,aiRotx,αi

(9)

式中：Rotz,θi为绕着z轴旋转θ度的变换矩阵；Transz,di为沿z轴方向，位移连杆长度为d的变换矩阵；Transx,ai为沿x轴方向,连杆长度为a的变换矩阵；Rotx,αi为绕x轴旋转α角度的变换矩阵。

把得到的KUKA机械臂的D-H参数带入到旋转矩阵中，得到机械臂的变换矩阵模型，即

(10)

(11)

式(10),(11)中分别给出了A1和A2的值，同理可求出A3～A6的值

2.2.3末端执行器与机械臂末端轴的转换

末端执行器的姿态采用双向量法描述，如式(4)所示。末端执行器{O7}和机械臂轴末端{O6}的姿态变换矩阵bAm可以通过末端执行器的设计图纸求出

(12)

因此，末端执行器所建立的坐标系{O7}与机械臂基坐标系{O1}之间的转换关系为

7Tb=7A66A55A44A33A22A11Ab

(13)

2.2.4激光跟踪仪坐标系与机械臂基坐标系转换

在目标引导系统中，机械臂基坐标系{O1}与激光跟踪仪的坐标系{O0}的相互转换至关重要。机械臂基坐标系{O1}[11-12]和激光跟踪仪坐标系{O0}的齐次变换矩阵为

(14)

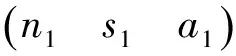
因此，从末端执行器所建立的坐标系{O7}到激光跟踪仪的坐标系之间的转换关系为

7Tm=7A66A55A44A33A22A11AbbAm

(15)

2.3 被测目标模型建立

被测目标模型是根据设计图纸建立的。不同的被测物体的模型不同，任何一批被测物体在第一次被测之前都需要根据设计图纸建模。本文以棱柱体为例建立被测目标模型，如图5所示。

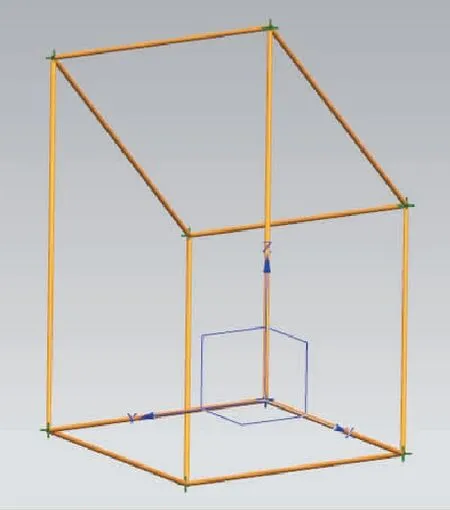
图5 目标点模型

该目标有8个棱角，从上面的4个棱角中，任意选取一点A作为被测点来求取目标点的位置和姿态信息。

2.3.1目标点的位置模型

A点在被测目标坐标系{O7}中的位置为(x1,y1,z1)。为了确定被测目标点在激光跟踪仪坐标系{O0}下的位置信息，需要建立激光跟踪仪坐标系{O0}和被测目标坐标系{O7}之间的齐次变换矩阵。本文采用四点法求取齐次变换矩阵，这4个点分别为：激光跟踪仪在被测目标坐标系{O7}中的原点、x轴上的一点、y轴上的一点、z轴上的一点。求取从被测目标点的坐标系{O7}到激光跟踪仪的坐标系{O0}之间的齐次变换矩阵为

(16)

A点在激光跟踪仪坐标系{O0}下的坐标由式(17)计算

(17)

2.3.2被测目标点的姿态模型

一般情况下，点是不存在姿态信息的，但是因为本系统中存在激光跟踪仪和反射镜，故根据系统的实际情况，为被测目标点定义方向，即将点到激光跟踪仪头的方向向量定义为被测目标点的姿态。

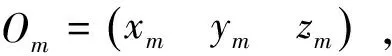
(18)

式中：xmm=xm-x1m；ymm=ym-y1m；zmm=zm-z1m。

2.4 总结

对于整个测量系统，机械臂的末端执行机构在激光跟踪仪坐标系{O0}下的最终位姿需和被测目标点在激光跟踪仪坐标系{O0}的位姿相匹配，从而计算机械臂各个轴需要调整的角度。整个系统模型组成如图6所示。

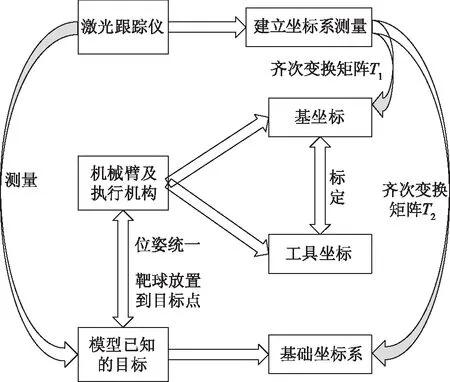
图6 系统组成

3 仿真和验证

通过坐标系的齐次变换矩阵，将建立的激光跟踪仪、机械臂、被测目标的模型转换到激光跟踪仪的坐标系{O0}中。利用Matlab中RTB工具箱对整个模型进行仿真分析，验证其准确性。

图7是由Matlab画出的示意图。坐标系{O}代表的是激光跟踪仪所建立的坐标系{O0}。坐标系(x1,y1,z1)代表被测目标点的位姿。KUKA末端坐标系代表机械臂末端轴坐标系{O7}，该坐标系的z轴为靶球的开口方向，因已知目标点的位姿(坐标系(x1,y1,z1)的原点代表被测点的位置信息，z轴方向表示距离姿态信息) ，故通过Matlab求出机械臂各个轴的角度，如图7所示。

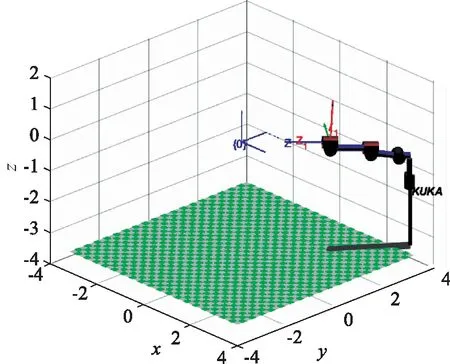
图7 坐标系的统一

图7中末端轴坐标系{O7}的z轴朝向激光跟踪仪头，在不同的视角下的图像如图8所示。

从图8中可以看出，机械臂的末端执行器的位姿与目标点的位姿相同，从而证明了模型的准确性。

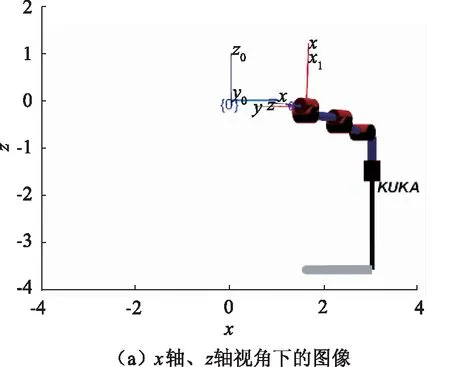
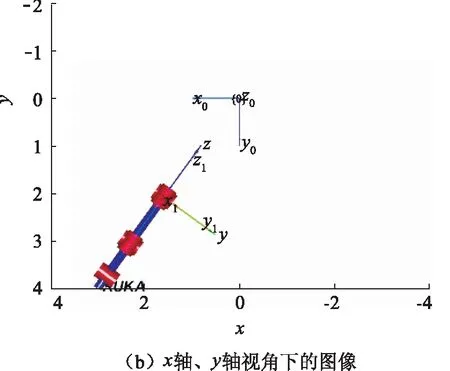
图8 不同视角下的图像

4 结论

为了实现激光跟踪仪的自动测量，建立了一种利用机械臂抓取靶球的目标引导系统。详细分析了刚体位姿描述的方法，并根据目标导引系统的实际情况，分别建立了激光跟踪仪、机械臂及被测目标的理论模型。将所建立的激光跟踪仪坐标系{O0}作为基础坐标系，将机械臂的基坐标系{O1}和被测目标的坐标系{O7}进行统一，最后通过Matlab仿真分析，验证了该模型的可靠性和方案的准确性。本文介绍的目标引导系统可解决目前激光跟踪仪无法全自动连续测量的问题，其中模型的建立和仿真实验为未来相关研究工作提供了参考依据。