一种复杂曲面检测的改进最小二乘方法

， ， ，， ，

(1.辽宁省数控机床信息物理融合与智能制造重点实验室, 辽宁 抚顺 113122；2.沈阳工学院 机械与运载学院，辽宁 抚顺 113122； 3.沈阳音乐学院 艺术管理系，沈阳 110168)

0 引言

对复杂曲面的检测是现代检测过程中，面临的重要问题，随着中国制造业的跨越式发展以及高端制造业的实际需求，零件的加工向着复杂化、精密化的方向发展[1]。上述发展方向对零件的加工精度及检测精度提出了更高的要求[2-3]。叶轮作为动力机械的关键部件，目前在航空、造船、发电、风机等行业得到广泛应用[4-5]。叶轮叶片属于自由曲面，叶片扭曲严重，测量时易发生干涉，且要求全尺寸检测，项目较多，检测效率低下，被视为制造业中的难题之一[6-8]。目前，常采用整体叶轮叶片型面展成运动轨迹的计算方法[9]、数字样板检测法[10]和基于曲率的测量点采样方法[11]。上述测试方法虽然存在现场使用方便，检测迅速，费用低廉的优点，但存在测量精度不高，且叶片上的坐标点属于空间三维曲面上的点，测量时需采用三维补偿[12]，轮廓度评价时需要采用六维最佳拟合[13]，因此，对测量软件算法和机器精度要求很高。陆峰等提出了一种三维检测方法，该方法是基于光学测量和计算机图形图像处理相结合的技术[14]。刘涛等提出了一种以3D数字化模型为基础的检测方法，该方法主要针对复杂三维型面涡旋零件的精度进行检测(方法是利用三坐标测量机获取涡旋零件的表面点云数据，再借助于Geomagic Qualify三维检测软件对获得的数据进行处理，该方法实现了检测结果的可视化[15]。关娟等针对复杂曲面重点研究了如何利用最小二乘法进行非线性曲线的数据拟合问题求解，并基于VB语言与Matlab语言结合的方式进行了数据处理系统软件的设计，通过实际结果表明，该文中提出的算法具有非常好的拟合效果，并通过实际工程项目进行了检验[16]。

文献[17]针对风电机组中的主轴承实时状态测量问题给出了一种基于深度信念网络(DBN)的监测方法。文献[18]基于风电机组中的主轴承故障检测采用了SCADA数据处理的检测方法。相比于主轴承的检测来说，叶轮叶片的型面更为复杂，对发动机性能影响较大，其故障率相对较高，若发生故障，会造成无法估量的损失，因此，研究有效的叶轮叶片检测方法对发动机行业意义重大。

本文采用三坐标测量机结合PC-DIMS软件叶轮叶片进行检测，基于迭代法进行坐标系建立，并进行叶轮叶片的曲面检测，提出利用最小二乘法进行数据处理与求解。

1 三坐标测量机工作过程及复杂曲面检测分析

1.1 三坐标测量机工作过程

三坐标测量机的工作原理是在三维可测的空间范围内，能够根据测头系统探测工件，返回工件表面的点数据，通过三坐标的软件系统(如AC-DMIS)计算各类几何形状、尺寸等测量能力的仪器。

在空间中，可以用坐标来描述每一个点的位置，多个点可以用数学的方法拟合成几何元素，如：面、线、圆、圆柱、圆锥等。利用几何元素的特征，如：圆的直径、圆心点、面的法矢、圆柱的轴线、圆锥顶点等可以计算这些几何元素之间的距离和位置关系、进行形位公差的评价，以上就是三坐标的工作原理[15]。由此可见，三坐标测量机的这一工作原理使其具有很强的通用性与柔性。从原理上说，它可以测量任何工件的任何几何元素对应的几何参数。

三坐标测量机种类繁多、形式各异、性能多样，所检测对象和放置环境条件也不尽相同，是典型的机电一体化设备，大体由机械系统(主机)、探测系统(测头)、电气系统(操纵盒)、以及软件系统(计算机)四部分组成[19]。

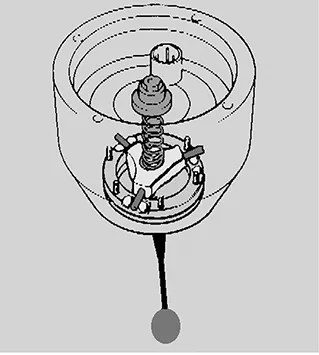
图1 机械测头示意图

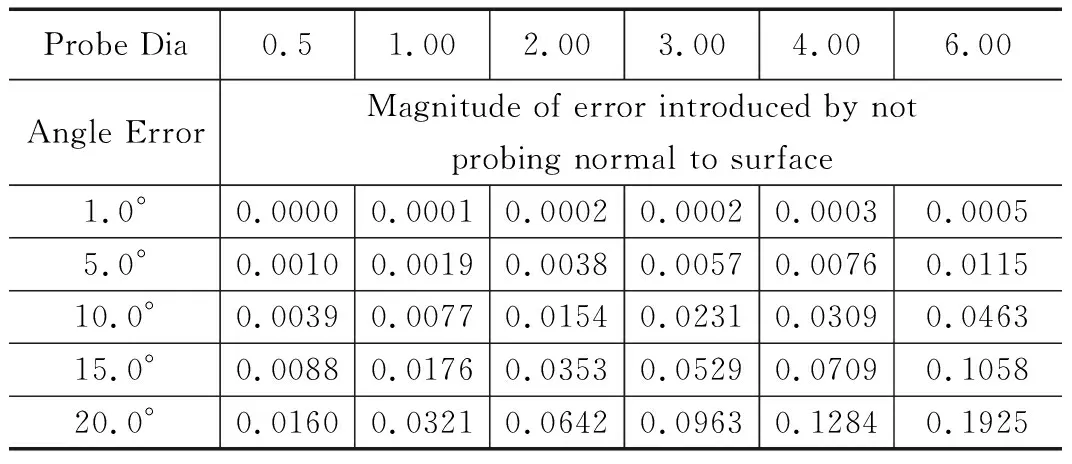
表1 不正确的矢量及相关误差表

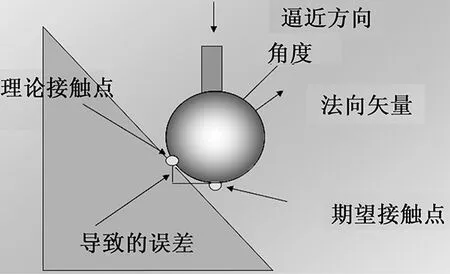
图2 不正确的矢量及相关误差

正如TP20这样的机械测头，包括3个电子接触器，当测杆接触物体使测杆偏斜时，至少有一个接触器断开，此时机器的X、Y、Z光栅被读出。这组数值表示此时的测杆球心位置。

1.2 复杂曲面检测分析

叶轮(impeller)，又称工作轮，属于复杂曲面的一种。叶轮作为动力机械的关键部件，目前在航空、造船、发电、风机等行业得到广泛应用。叶轮叶片的型面非常复杂，对发动机性能影响大，设计研制周期长，制造工作量大。其加工、检测一直被视为制造业中的难题之一，叶轮加工过程中的全面质量控制是叶轮制造过程中的重要环节。

叶轮检测的难点在于：

1)叶轮叶片属于自由曲面，叶片扭曲严重，测量时易发生干涉。

2)叶片上的坐标点属于空间三维曲面上的点，测量时应采用三维补偿，轮廓度评价时需要采用六维最佳拟合，对测量软件算法和机器精度要求很高。

3)效率和精度要高。叶轮通常要求全尺寸检测，项目较多，无法从效率上满足要求。

叶轮三维视图如图3所示。矢量点和自动圆如图4所示。图 5为叶轮加工工艺图。

图3 叶轮三维视图

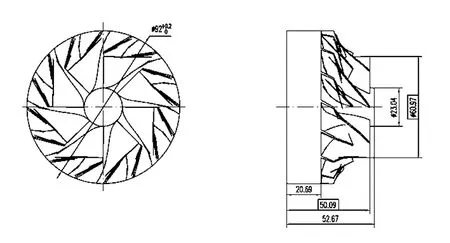
图4 矢量点及自动圆

图5 叶轮加工工艺图

2 复杂曲面检测方法

2.1 坐标系建立原理

迭代法原理：迭代法建立坐标系主要应用于工件原点不在工件本身、或无法找到相应的基准元素(如面、孔、线等)来确定轴向或原点的零件。迭代法建立坐标系特征元素必需要有数模或用于建立坐标系的元素的理论值信息。

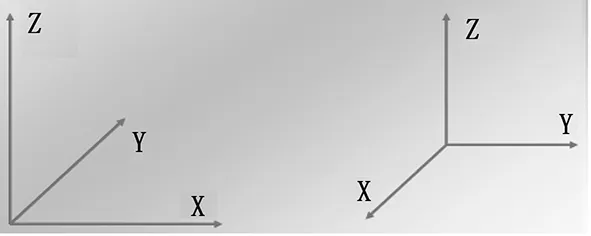
图6 确定直角坐标系坐标轴

本次测量叶轮采用六点迭代法建系，使其测量点拟合为平面、直线、点，再利用3-2-1法创建坐标系。其六点法迭代建立坐标系的算法步骤如下：

Step1：确定3个矢量方向近似一致的矢量点。

Step2：将3个矢量点进行拟合确定一个平面，目的是找正一个轴向。

Step3：确定两个矢量方向近似一致的点，并且此两点的连线与前3个点方向垂直。

Step4：将两个矢量点进行拟合，确定一条直线

Step5：通过旋转确定第二轴。

Step6：将最后一个矢量点设定为原点。

Step7：要求该点的方向与前5个点矢量方向均垂直。

结合叶轮形状，为精确建立坐标系，本文采用在叶轮下表面打3个矢量点来拟合平面，在叶片上部测量2个矢量点进行直线的拟合，在叶轮上表面打出矢量圆来进行坐标原点的拟合。

2.2 进行矢量点自动圆的选择

矢量点自动圆的选择算法：

Step1：测量模式首先调整为手动模式。

Step2：打开自动测量圆对话框，在数模上选取圆，圆上表面“采样例点”必须为3个，间隙-2。

Step3：根据图片所示修改中心坐标x、y数值，鼠标点击自动圆上表面z的测量值自动填入。

Step4：根据叶轮图纸参数，输入测量点为8，圆柱深度-1。测量点的深度-0.2。调整触点在各叶片中间。

Step5：当自动测量圆时，为防止测头撞到圆弧，应修改逼近距离、回退距离，(在程序开头把逼近距离改为2，回退距离改为3)。注意避让移动为两者，距离为40。

图7为测量点的布局图。

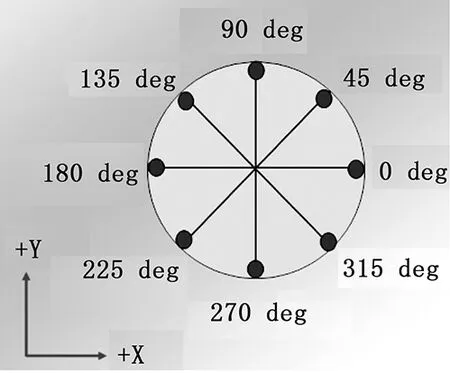
图7 测量点布局图

2.3 复杂曲面坐标系建立方法

Step1：点击插入-坐标系-新建-进入迭代法建立坐标系。

Step2：依次选择矢量点1.2.3.4-z轴。

Step3：依次选择矢量点5.6.7-x轴。

Step4：依次选择矢量点圆1-原点。

Step5：勾选“始终测量全部特征”。

Step6：打点次数选择5或其他数值。

Step7：点目标半径0.1或其他(数值越小精度越高)。

Step8：确定。

算法执行，依据算法中的打点顺序依次测量所有矢量点。最后一个矢量点输入完成后，测量机便会自动进行迭代运行。

2.4 复杂曲面阵列确定及测量

2.4.1 复杂曲面手动打点并测量

叶片手动打点并测量算法步骤如下：

Step1：进行特征-矢量点的插入。

Step2：在数模的叶片上进行测量点的选择。选择原则：测量点选择要均匀，数量越多评价的尺寸越精确，但耗时越长。

Step3：确定最后一个测量点是否选择完成，如果是，转Step4；否则，转Step2。

Step4：移动z轴，提升到距离叶轮上表面5～10 mm处，并进行安全点的记录。

Step5：进行点的测量，并记录相关数据。

Step6：所有测量点是否测量完毕，如果是，则转Step7；否则，转Step5。

Step7：结果输出。

2.4.2 获取复杂曲面阵列

Step1：复制所有测量点，在编辑窗口中选择叶片上所有测量点进行复制。

Step2：修改阵列列表，点击编辑列表-阵列，在阵列设置中修改偏置角度(45)、镜像(无翻转)、偏置次数(7)。

Step3：阵列粘贴，光标放到编辑窗口底部，点击编辑列表-阵列粘贴。

Step4：叶轮中所有大叶片测量点自动生成。如图8所示。

图8 叶轮叶片所有测量点

3 改进的最小二乘方法

最小二乘法(LS)作为一种最基础、最经典，同时也是最广泛应用的曲线拟合方法，应用范围异常广泛，但也存在一定的问题：最小二乘曲线拟合的非一致的，即具有一定的偏差性。因此，为了克服改缺陷，本文采用一种改进的最小二乘法：广义最小二乘法。用于解决复杂曲面零件的检测问题[20]。

一个零件在其加工过程中，实际加工精度与其设定值难免存在差距。为提高测量精度，避免测量误差，就需要更多的测量点，这也导致了测量过程时间的加长。

叶轮叶片型面为复杂曲面，因此，本文采用基本测量点数拟合几何特征的最小二乘法导出非线性的数学方程，并转换为线性化方程进行求解。算法运算过程如下：

首先，由上述测量点5、点6、点7拟合一条理想直线方程，具体拟合数学过程方法如下：

设直线所在的工作平面为XY,Pi(xi,yi)(i=1,n)为测点的集合，设定理想拟合直线方程为：

y=ax+b

(1)

由最小二乘法原理知，目标函数为：

(2)

由于函数a和b的偏导数为零，因此可解直线的参数值为：

(3)

(4)

该直线通过(0，b，0)，其单位方向向量为：

(5)

其次，由上述测量点1、点2、点3、点4拟合理想平面，具体拟合过程算法如下：

设N个测量点为Pi(xi，yi，zi)(i=1,2,…,N)，则理想平面方程为：

z=Ax+By+C

(6)

由最小二乘法原理可知，目标函数为：

(7)

直线的参数值为：

(8)

(9)

(10)

平面的单位向量(l，m，n)为：

(11)

(12)

(13)

最后，由上述测量自动圆的圆心来拟合坐标原点，具体拟合算法如下：

设测量工作平面为X，Y，N，测量点为Pi(xi,yi,zi)(i=1,2,…,N),则理想的圆方程为：

(x-x0)2+(y-y0)2=R2

(14)

由最小二乘法原理，目标函数为：

(15)

由于本函数的偏导数为非线性方程组，为求解方便，对函数进行线性化处理:

(16)

(17)

本文改进的最小二乘法的处理过程如下，假设该系统采用的模型如下：

(18)

其中:A(z-1)，B(z-1)和C(z-1)的定义如式(19)和(20)所示：

(19)

(20)

na，nb和nc作为模型的阶次，在本文中假定是已知的，采用改进的广义最小二乘法可以得到上式的无偏一致估计。有如下的两个假定：

(21)

及:

(22)

将模型化为最小二乘格式：

(23)

由于v(k)是白噪声，所以用最小二乘可以获得参数θ的无偏估计，由于噪声模型C(z-1)未知，还需要用迭代的方法来求得C(z-1)。令:

(24)

置:

(25)

这样就把噪声模型也转变为最小二乘格式：

(26)

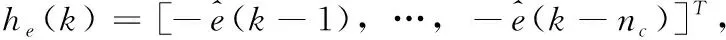
(27)

计算，式中,

h(k)=[-z(k-1),…,-z(k-na),u(k-1),…,u(k-nb)]T

(28)

综上所述，改进的广义最小二乘法可归纳为：

(29)

上述算法流程如图9所示。

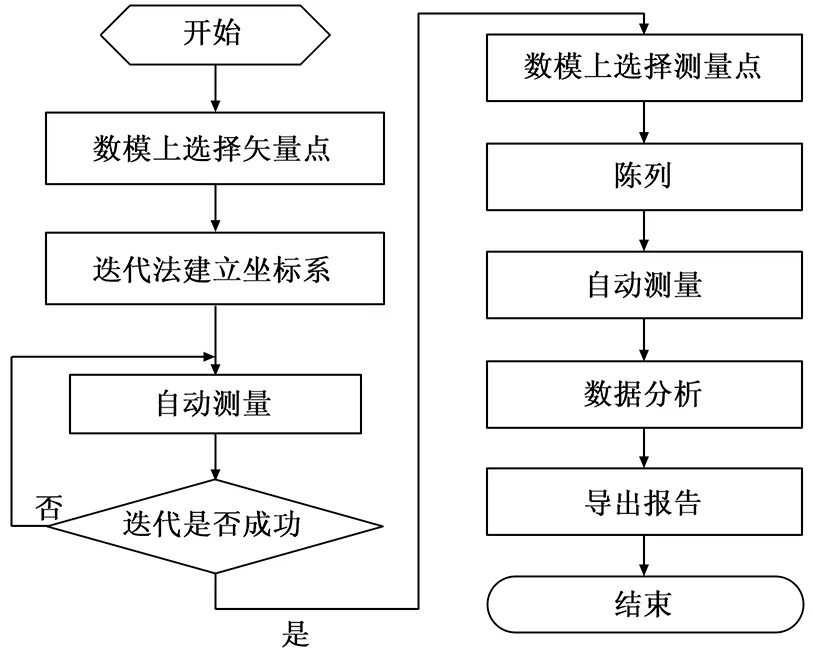
图9 算法处理流程图

4 复杂曲面实际测量及结果分析

利用辽宁省数控机床信息物理融合与智能制造重点实验室中的海克斯康三坐标测量机，对叶轮采用上述算法进行了实际检测。

具体检测步骤如下：

Step1：点击评价栏中“特征位置”界面，选择叶片中所有测量点，勾选薄壁件选项(T)，输入公差进行创建。

Step2：点击视图，调出表格显示窗口。

Step3：按照上述算法进行叶轮测量。

Step4：叶轮测量完成，输出测量结果。

本文选取了8个叶轮。并利用PC-DMIS数据分析软件进行测量点分析，在每个叶轮上选取点如图10所示。

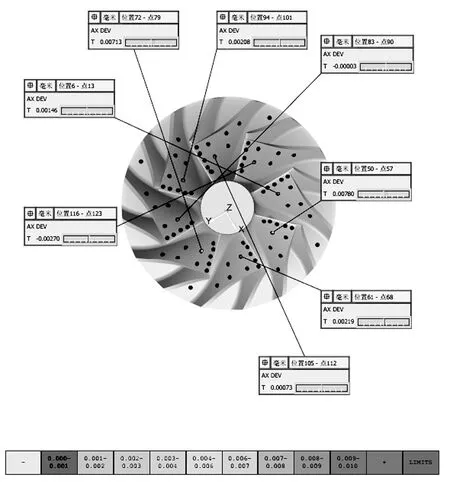
图10 叶轮选取点示意图

针对图11中选取的点，进行了实际测量，在叶片数模上打点的理论值与实际测量值的偏差如表2所示。

针对表2中的偏差计算出了平均值和方差折线统计图，如图11所示。

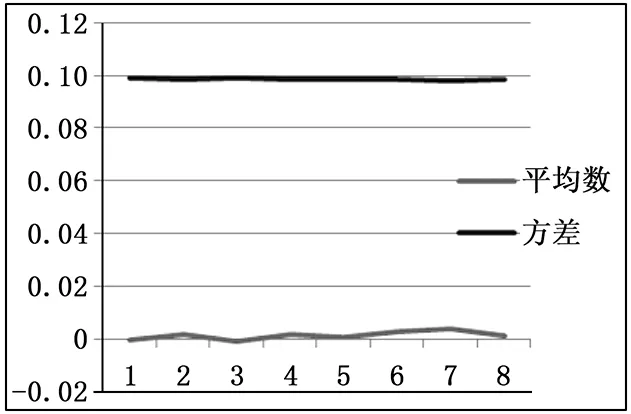
图11 偏差平均数及方差折线图

表2中采用上述检测方法检测了四组叶轮，每个叶轮随机抽取8个测量点进行抽样检查，所有点的检测结果都在误差允许的范围内，通过均值、方差和误差来看，也都满足指标要求。

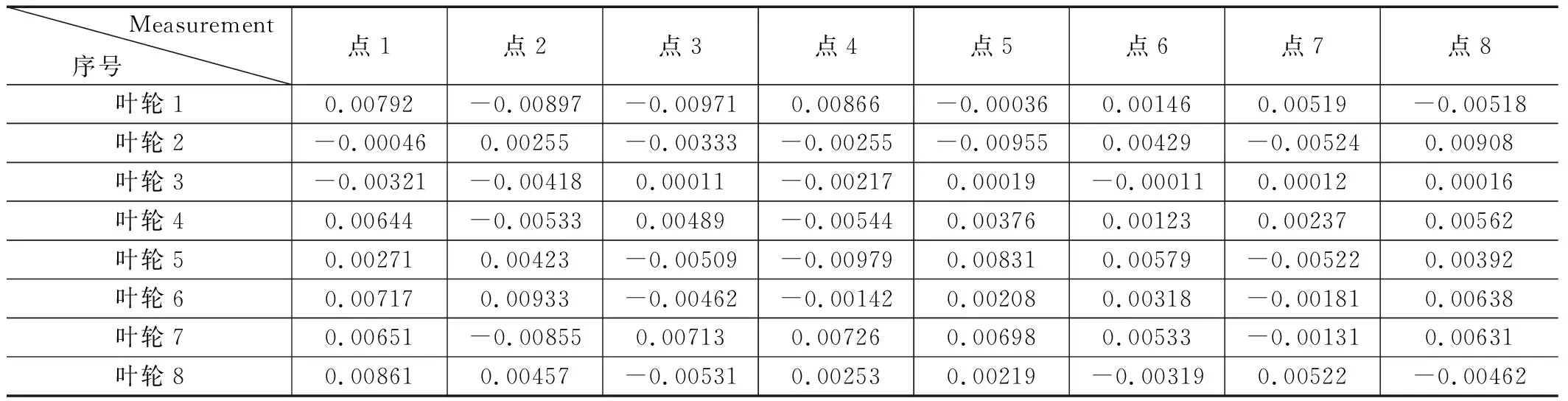
表2 所选测量点的测量结果及误差

图12为实际的检测结果部分结论(图中点偏差颜色显示为超差范围)。

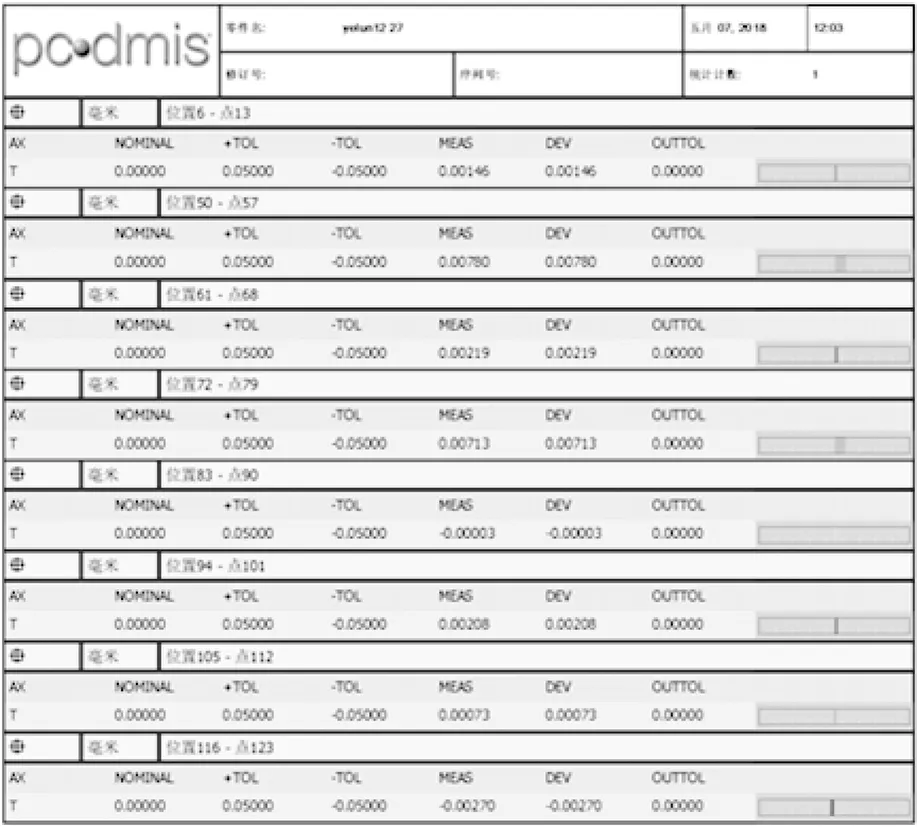
图12 检测结论

5 结论

通过用迭代法建立复杂曲面叶轮的坐标系，并借助于海克斯康三坐标测量机和PC-DIMS软件进行了叶片曲面的实际检测，采用阵列粘贴的方式，利用最小二乘法进行数据拟合。结合计算机求解及数据处理，通过选取8个16片叶轮，每个叶轮检测8个点的数据分析结果可以看出，本文采用的检测方法，结果准确、可靠。此方法不仅适合于叶轮的检测亦可用于其它难以建立准确坐标系的曲面零件场合。在后续的工作中，将以此方法所建立坐标系为基础，收集其他曲面复杂零件进行检测，并对误差数据进行进一步分析，更好的指导测量过程。