内河物体漂移轨迹及其终点预测建模与仿真

刘 柯， 张 笛， 张金奋， 范诗琪

(武汉理工大学 a. 智能交通系统研究中心； b. 国家水运安全工程技术研究中心， 武汉 430063)

水路运输系统由于受到内外部复杂通航环境的影响，存在着很大的风险，一旦发生碰撞、搁浅和自沉等事故，往往会造成巨大的人员伤亡和财产损失。国际海事组织(International Maritime Organization, IMO)提出的综合安全评估(Formal Safety Assessment, FSA)可以从降低事故发生的概率和降低事故造成的后果两个角度来实现有效的风险管理。[1]降低事故发生概率的主要方式是对影响风险的关键因素进行有效识别和定量评价，并提出最有效的风险控制策略；而在水上交通事故发生后，快速、准确和有效的应急搜救行动是救助人命、降低财产损失最有效的手段之一。水上交通事故发生的过程中往往伴随着人员和货物的失踪，失踪物体在漂移过程中受到风、流、浪等的影响，如何准确预测失踪物体的漂移轨迹，获取其漂移后最有可能的位置或目的地，对于应急资源的调度和救援行动的快速开展起着重要作用。美国海岸警卫队将搜救分为3个步骤[2]：

1) 获取失踪物体周围环境数据，主要包括风、流和浪等信息。

2) 根据环境数据预测失踪物体的可能位置，通常用概率密度分布函数表示。

3) 根据概率密度分布函数制定最有效的搜寻路径最优方案。

关于水上失踪目标的漂移轨迹预测问题，目前的研究主要集中在海上，预测模型主要包括CANSARP模型[3]、HACSALV模型[4]和Leeway模型等。[5]从研究方法来看，主要有基于实际场景试验获取观测数据的统计、实验室模拟环境下的漂移建模和基于模拟仿真的动力建模等3种预测方法。

1) 研究以挪威和美国为代表，例如BREIVIK等[5]在北海水域开展大量的海上漂浮物体轨迹漂移试验，总结出63种不同类型物体的漂移规律，这些物体主要包括人、自由航行船舶、非机动船舶等，并根据水面以上部分所占比例进一步分为若干子类，总结出不同类别物体的漂移规律，这对于失踪物体轨迹的预测具有重要的参考意义。

2) WANG等[6]基于漂移物体的形状搭建的漂移轨迹预测试验平台，通过对漂移物体受风、流和浪单独影响和综合影响多种场景下的数据进行分析，建立漂移轨迹预测统计模型。

3) Özgökme等[7]基于Leeway模型和拉格朗日模型建立的海上不规则流场下的物体漂移轨迹预测模型，研究风场和流场密度对预测精度的影响。ZHANG等[8]建立同构流场下失踪物体漂移轨迹预测概率模型，通过风速和流速的预测不断更新物体的位置，仿真结果表明该模型具有较高的精度和可靠性。

以上研究主要是针对海上失踪物体位置的预测的，而针对内河失踪物体的研究则相对较少。李琳琳等[9]以川江为例研究失踪人员搜寻区域的确定方法，利用风致漂移、风生流致漂移和水流致漂移的规律，总结时间推移下落水人员的漂移规律，可对人员漂移的距离进行估计，但是不能更进一步预测人员漂移具体位置。于卫红等[10]通过计算机程序实现总水流矢量计算、风压差计算及位置的总或然误差计算，提出确定搜寻目标漂移后的搜寻区域的具体方法。该研究是基于物体位置报告及风、流、浪等信息的基础上实现的，对研究工作有很好的指导意义。

在Leeway模型的基础上，首先基于内河流场的统计特征，建立风流影响下漂移速度预测模型，利用风流场数据的不确定性特征不断更新失踪物体的可能位置，然后结合航道岸线特征，预测失踪物体最终可能漂移终点位置的分布情况。

1 失踪物体漂移模型

1.1 Leeway模型

水上漂移物体主要受到风、流、浪的作用力，有研究[5]表明，当波高小于物体尺寸的1/30时，波浪的影响作用可以忽略不计。本研究仅考虑风和流对物体的作用。根据风流漂移模型，物体在达到稳定漂移状态时，受力情况为

|VB-VC|(VB-VC)

(1)

式(1)中：CD阻力系数；A物体裸露部分的截面积；ρ为流体密度；下角标1、2分别为物体暴露空气中和浸没在水中部分的阻力系数、截面积及流体密度。假设定义

(CDAρ)1/(CDAρ)2=λ2

(2)

漂流物体的速度VB为

(3)

VB=VC+f(VW-VC)

(4)

以上模型通常被称作Leeway模型，可发现当风速和流速能精确获取时，漂移物体的速度预测就较为精确。然而实际情况中风场和流场往往存在很大的不确定性，导致漂移物体的运动速度预测也会存在一定的偏差，在轨迹预测时需要加以考虑。

1.2 漂移轨迹预测

一个物体在内河航道漂移，受到水流和风力的作用，假设在一定时间Δt内漂移速度相对稳定，那么物体的位置从tn时刻到tn+1时刻的更新为

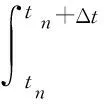
(5)

式(5)中：Vt为tn时刻的物体漂移速度，漂浮物经一时间步长Δt后漂移至Stn+1。式(5)一般被称为欧拉-拉格朗日追踪法。如果Δt足够小，漂移物体的运动轨迹可以被近似分解成一系列离散的匀速运动的叠加，重复以上过程就可以不断更新物体的漂移位置。如第1.1节所述，在物体位置更新过程中需要考虑风场和流场的不确定性对漂移速度的影响。此外，失踪物体的初始位置在实际中往往不精确，而是以可能存在的区域表示。因此，将物体可能的初始位置区域内的流场所在位置用矩阵表示为

(6)

上述区域内的流速场会对物体漂移速度产生影响，因此首先将该区域内所有流场数据提取出来，假设该区域流速场用以下两个矩阵表示为

(7)

由于获取的内河流场存在不确定性，现赋予每个流速数据存在一个上下偏量角度α，即每个坐标点位置处的流向的可能范围为

θC∈[θC-α,θC+α]

假设物体可能的位置在区域内为均匀分布，那么流场内每个点都有可能会对其产生影响，根据Leeway模型，以流场中Xij位置为例，假设物体处于该位置，那么物体可能的速度计算为

VBx1=Vijcos(θij-α)+f[VWcosθw-

Vijcos(θij-α)]

(8)

VBy1=Vijsin(θij-α)+f[VWsinθw-

Vijsin(θij-α)]

(9)

VBx2=Vijcos(θij+α)+f[VWcosθw-

Vijcos(θij+α)]

(10)

VBy2=Vijsin(θij+α)+f[VWsinθw-

Vijsin(θij+α)]

(11)

式(8)～式(11)中：下角标x、y分别为物体漂移速度在经度、纬度方向的分量；下角标1、2分别为水流的方向角分别为θij-α和θij+α。因此，Xij处物体的漂移速度为

VBx∈[VBx2,VBx1]VBy∈[VBy1,VBy2]

(12)

则经过Δt后，Xij坐标位置处物体的漂移位移为

Lx=VBxΔt∈[VBx2Δt,VBx1Δt]

(13)

Ly=VByΔt∈[VBy1Δt,VBy2Δt]

(14)

将区域S0流场内所有速度都按照相同的方式处理，可以求得初始区域S0经过Δt时间后其在方向运动的最远位置Xmax和最近位置Xmin，同理也可求得Ymax和Ymin。漂移物体的位置为

(15)

漂移物体经过Δt后，位置就可以更新到新的区域，按照同样的方式即可更新物体可能的区域范围。

1.3 模型合理性分析

提出的轨迹预测模型是在Leeway模型的基础上考虑环境中风、流的影响，获得物体的漂移速度大小和方向。在漂移过程中物体形状的不对称性以及环境中风速、流速方向的不稳定性，都将影响物体漂移速度方向的不确定性，因此采用区间法设定任一质点位置处物体的漂移速度满足区间θC∈[θC-α,θC+α]。

研究中用矩形区域表示物体可能存在的位置，采用穷举法计算区域内所有质点位置物体的漂移速度范围，当Δt时间足够小时，物体的漂移运动可以假设为匀速运动，将区间内任一质点位置进行更新，得到Δt后物体的更新区域，因此在理论上有一定的可靠性。

1.4 物体漂移终点预测

对物体漂移终点预测的准确程度，将直接决定搜寻行动的针对性，从而影响搜救的效率，见图1。假设物体漂移位置在预测的矩形范围内服从均匀分布且漂移物体触及岸线则停止漂移。在tn时刻物体的预测区域为ABCD，tn+1时刻的预测区域为A1B1C1D1，两块区域都和岸线相交，交点分别为E、F和G、H，因此，在tn和tn+1时刻漂移物都有可能成为漂移终点。

假设tn为漂移物第一次有可能触岸的时刻，按照均匀分布的特征，在tn时刻漂移物触岸的概率以及其在岸线EF段的概率密度分别为

(16)

(17)

需要注明的是概率密度等于一段区间的概率除以该段区间的长度。

在tn+1时刻漂移物触岸的概率为Pn+1，但计算Pn+1的前提是tn时刻物体没有触岸，仍然处于漂移状态，则可得Pn+1为

(18)

从图1可知：在tn+1时刻漂移物可能到达岸线GH段，其中GF段为tn、tn+1时刻的重合段，这就表示GF段的概率密度为tn时刻与tn+1时刻在GF段的岸线概率密度之和：

(19)

PLGF=PLEF+PLGH

(20)

2 仿真与讨论

2.1 参数设置

利用模拟仿真的方法对提出模型的性能进行测试和比较分析。失踪物体在落水后，将会在风、流和浪等自然环境因素的影响下离开初始事故地点[11]，当漂移到岸边后，将会由于水深较浅而停留在岸边。

为了模拟这一过程，需要确定仿真中参数的设置问题，主要参数的取值见表1，其中流速和流向是指主流中的最大水流。根据内河水流中间流速大，两边流速小、流速具有一定紊乱性等特征，利用MATLAB随机生成一个内河流场，其中流场的不确定性为流速方向的20%。内河流场一般比海洋环境下的复杂，而流场模拟不是所研究的重点，本节利用随机模拟的方法生成一个流场作为案例研究。考虑到流速一般取值较小，物体漂移速度一般较小，其位置更新频率取为10 min。此外，参数f反映漂移物体水面以上部分所占的比例情况，由此可以看出，λ越小，f就越小，表示物体在水面以下的部分越大。本研究采用文献[12]中的取值0.13，此类物体大部分都处于水面以下，例如落水人员和集装箱等。

在以下模拟中，漂移物体最终位置的概率分布是在给定的内河环境中利用上述算法进行计算获得的，通过不同参数设置下各因素的不确定性分析和比较来研究各参数对预测结果的影响见表1。

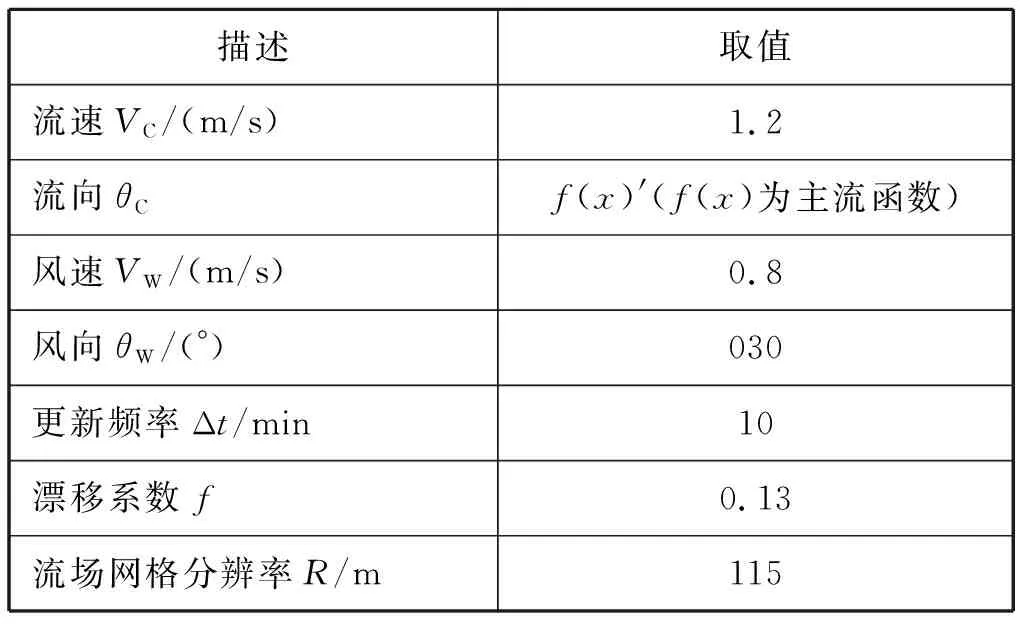
表1 仿真参数设置

2.2 漂移轨迹预测及其最终位置概率分布分析

利用以上设置的相关参数，得到的内河水域中的流场分布见图2。图2中同时标示漂移物体在不同时刻可能位置的区间范围，当矩形区域与航道边界存在交点时，就存在停止继续漂移的可能性，假设物体的可能位置在相应时刻在矩形区域内为均匀分布，可得到物体最终漂移位置的概率分布情况。

由图2a)可知：物体在漂移了80 min后第1次出现和岸线相交的情况。随着时间的推移，矩形区域逐渐扩大，表明物体轨迹的预测精度在逐渐下降，而且预测区域一直存在和河岸相交的情况且相交的区域越来越大。该结果表明：在第80 min时刻，物体就有可能触岸搁浅，但此时搁浅的概率较小，随着时间的推移，物体停止漂移的概率将越来越大，当到达峰值后就将逐渐减小。由图2b)可知：漂移物沿岸线最终停止的位置距初始位置的下游距离概率分布情况呈现出先增加后减少的变化趋势，变化幅度较大。

漂移物体初始位置改变时物体漂移轨迹预测结果及物体漂移终点概率分布见图3，流速下降20%时物体漂移轨迹预测结果及物体漂移终点概率分布见图4。

由图3a)可知：在漂移50 min后第1次出现和岸线相交的情况。随着时间的推移，预测区域不断扩大。由图3b)可知：漂移物沿岸线的搁浅概率仍然呈现先增加后减少的变化趋势，变化幅度较初始位置没变时更为平缓，分布更加发散。分布的期望处于4 400～4 800 m。比较图2和图3，初始位置的改变不能影响触岸概率的变化规律，但其对漂移物首次触岸的时间、概率分布的幅度、发散程度和期望区间都有一定程度的影响，初始位置离岸越近，其第一次可能触岸的时间越短、概率分布的幅度越小，发散程度越大，期望区间越靠后。这表明物体漂移的最终位置分布较为分散，预测精度相对较低。

由图4a)可知：物体在漂移了90 min后第1次出现和岸线相交的情况，且随着时间的推移，预测区域不断扩大。由图4b)可知：漂移物沿岸线的搁浅概率同样呈现先增加后减少的变化趋势，变化幅度与图2比较区别不大。分布的期望处于4 400～4 800 m。仿真结果表明流速的改变同样不能影响触岸概率的整体变化规律。

3 结束语

受人员、船舶和通航环境等因素的影响，内河水上交通事故时有发生，而快速有效的水上搜救是降低事故带来的直接经济损失和人员伤亡的关键所在，而实施水上搜救的关键问题之一就是能够对失踪物体的漂移轨迹进行精确的预测，从而提升搜救的针对性。针对这一问题，采用Leeway模型和拉格朗日追踪法对漂移物体的轨迹进行预测，然后结合航道边界特征提出物体最终漂移位置的预测方法，利用MATLAB软件实现模型仿真，仿真结果表明：提出的模型能够在一定程度上体现内河失踪物体漂移的基本规律，能够根据风流特征预测物体最终漂移位置的分布情况。

在预测精度方面提出的模型还有进一步提升的空间，例如进一步考虑流场数据的空间相关性，进一步降低不确定性，从而提升漂移轨迹预测精度。此外，提出的方法仅从数值模拟的角度分析比较，其有效性还需要与实际场景下物体漂移轨迹进行比较，这也是未来研究的一个重要方向。