面向单向航道通航能力的船舶减速概率

王 展, 刘克中,2,3, 杨 星,2, 杨 帆, 杨旭刚

(1.武汉理工大学 航运学院, 武汉430063；2.内河航运技术湖北省重点实验室, 武汉 430063； 3.国家水运安全工程技术研究中心, 武汉 430063)

单向航道是水路交通运输中常见的一种船舶航行形式。相比于双向航道，单向航道内的船舶航行受到更加严格的限制和约束，致使航道通航能力受到影响，因此,提升其通航能力尤为重要。对单向航道船舶通航能力及相关问题研究不仅对港口航道规划、船舶交通组织及管理等方面具有重要的理论支撑，还为双向航道相关问题的研究提供重要借鉴。当前，针对单向航道通航能力，主要从船舶交通流静态特征、船舶交通流动态特征及船舶交通流仿真等方面开展研究。

1)基于船舶交通流静态特征的航道通航能力的研究。通过交通流量或交通密度来推断某一水域的通航能力[1-2]，但是船舶交通流量与交通密度因不能容易、准确地获取。船舶自动识别系统(Automatic Identification System, AIS)的普及与应用，不仅使得船舶交通流量的统计简单易行，还为船舶速度分布的统计提供手段和方法[3]，通过对船舶主要交通流平均速度的统计为航道通航能力的评价提供一种更直观、更准确的方法。[1-2]

2)基于船舶交通流动态特征的航道通航能力的研究。通常采用排队论方法，将航道内船舶交通视为一个排队系统，以排队与服务均衡时的航道服务水平来评价通航能力。[4-5]排队论方法更多地考虑船舶交通流在整体上表现的动态特性，但对于船舶个体间的干扰关系考虑不足。当前针对船舶个体间的干扰关系，主要对航道内船舶航行状态变化[6]及船舶行为间的耦合关系[7]进行研究，从船舶干扰过程的相关影响参数中挖掘信息来衡量航道的通航能力。

3)针对航道通航能力的仿真研究。船舶交通流仿真是以离散事件仿真为基础而逐渐兴起的科学研究方法，当前，MATLAB[6]、ARENA[7]等软件的熟练应用为这一研究提供技术支持。仿真研究的关键在于仿真模型的设计与实现，其中船舶、船舶交通流的生成是要解决的主要问题，当前采用蒙特卡洛方法[6]和元胞自动机方法[8]相结合的方式来解决该问题。仿真方法的目标实现在于仿真结果的输出及结果分析，通常根据仿真输出参数对航道通航能力进行分析与评估。[6-9]

从当前单向航道通航能力的研究进展来看，主要侧重于对航道交通流量的统计，结合排队论方法及仿真方法对航道内船舶通过数量进行估计，而由于对船舶速度差异性的影响考虑不足，特别是船舶减速引起的航道通航能力的下降情况。本文构建以单向航道船舶减速概率为目标，通过构建确定的数学模型揭示影响单向航道船舶通行效率的机理，研究结果可为单向航道通航能力评价及船舶组织调度提供理论基础。

1 船舶减速对单向航道通航能力影响分析

1.1 单向航道及其船舶交通流特征

单向航道是指同一时间内只允许同一个方向通航的航道[10]，对于这样的航道，其船舶交通流特征主要表现为船舶的队列特性及船舶间速度的制约性。在单向航道中，船舶交通流的队列特性体现在船舶的跟驰行驶上，由于在单向航道内禁止船舶追越，船舶进入后呈现排队行驶的特征。[11]在船舶队列中，船舶间的制约性集中体现在慢速船舶的影响上，船舶在以队列状态行驶的过程中，船舶间的距离因速度差异而不断变化，慢速船舶的出现往往使得其与后续船舶间的距离逐渐减小，对后续船舶的交通产生了制约。单向航道内船舶交通过程见图1。

1.2 单向航道内船舶减速影响因素

船舶减速是一种常见的船舶操纵行为，而这一行为通常会对航道总体的通航能力产生影响。船舶减速对航道通航能力的影响主要体现在以下方面。

1)船舶减速会增加船舶占用航道的时间，后续船舶受船舶队列顺序的制约，造成船舶通航时间的延误，航道的利用率下降。

2)在船舶交通队列特性的影响下，船舶减速行为具有传递性，航道内船舶减速后，可能会造成后续船舶连续减速，由此导致航道整体通航能力降低。

对于船舶连续减速过程，此处称之为船舶减速连锁效应，该效应会导致航道内的船舶交通处于阻滞的状态，应尽量避免航道内发生船舶连续减速过程。

船舶减速过程对航道通航能力有着不可忽视的影响，通过挖掘船舶减速的影响因素对船舶减速过程进行调控，能有效缓解船舶减速对航道交通的影响。下面对船舶减速影响因素进行分析并提取船舶到达率、船舶速度分布标准差和航道长度等3个船舶减速影响因素。

1)船舶到达率(单位时间到达航道入口的航道数量)是描述航道入口处船舶到达频率的一项参数，船舶到达率越大，航道内船舶密度越高，船舶发生减速的可能性会提升。

2)船舶速度分布标准差是描述船舶速度差异的一项参数，而船舶速度的差异性是船舶发生减速的前提条件，船舶间的速度差异性越大，船舶发生减速的可能性越高。

3)航道长度是航道的固有属性，对于不同长度的航道，船舶通过航道的时间不同，而船舶减速过程实际上是船舶速度差异性随通航时间的累积过程，这一过程对航道长度具有明显的依赖性，航道长度越长，船舶减速的可能性会提升。

2 船舶减速概率模型构建

2.1 模型假设

对于单向航道内的船舶到达规律及船舶速度分布规律，作出如下假设。

2.1.1船舶的到达规律

假定到达航道入口的船舶数量为一个计数过程，每艘船舶到达时间是相互独立的，而且在充分短的时间区间上最多只到达一艘船舶。在数学上，这一过程一般采用泊松分布来描述，其中单位时间到达的船舶数量用参数λ表示。

2.1.2船舶的速度分布规律

任何船舶进入航道时，都有一个初始速度，该速度与船舶进入航道前的航行状态有关，一般船舶间的初始速度是各不相同的。本文假定船舶初始速度是随机取值的，并服从一定速度区间内的均匀分布。

2.2 船舶减速条件

船舶减速临界关系见图2。将相邻船舶的2个通航状态标绘在线段上，通过简化船舶减速过程描述来构建减速边界条件。图2中初始状态为船舶S2进入航道的时刻，其前方船舶S1匀速行驶在航道内，两船的初始间距为d0，船舶S1、S2的速度分别为v1、v2。在船舶速度关系为v2>v1的前提条件下，船舶S2与船舶S1间距离逐渐减小。图2中最终状态为船舶S1即将驶出航道的时刻，两船间的距离为d1。

根据上述相邻船舶的2个通航状态，船舶离开航道前发生减速，船舶间的初始间距与最终间距需满足的条件为

(1)

式(1)中部分参数可作如下简化:船舶的初始间距d0是船舶S2进入航道时船舶S1已行驶的距离;已知船舶到达航道的到达率为λ，则船舶到达的平均时间间隔为1/λ，这里令d0≈v1/λ;船舶的最终间距是船舶发生减速后的距离，对于减速过程，假设船舶减速后与相邻前船维持在安全距离D匀速行驶，即d1=D,则船舶减速条件可表示为

(2)

2.3 船舶减速概率模型

根据船舶减速条件，可计算船舶减速概率。已知船舶速度服从均匀分布，则对于图2中的2艘船舶，在船舶S1速度取某一数值后，船舶S2的减速概率积分表达式为

(3)

(4)

式(4)为单向航道内相邻两船间发生减速的概率。但对于一个形成稳定交通流的航道，航道整体的船舶减速概率无法通过单船的减速概率来描述。从航道整体船舶交通考虑，若航道在一段时间内总共通过了N艘船舶，根据数学期望的思想，可认为该航道内船舶发生减速的概率近似为

(5)

式(5)中：pi为第i艘船舶发生减速的概率。

3 船舶减速概率模型试验验证

3.1 单向航道船舶交通仿真试验

单向航道船舶交通流仿真采用蒙特卡洛算法，通过随机生成的思想来模拟船舶交通流，根据第2.1节对船舶交通流规则所作的假设，船舶到达航道根据泊松分布随机生成，船舶到达时的速度根据均匀分布随机生成。

为了研究航道内船舶减速概率与船舶减速影响因子间的联系，并验证船舶减速数学模型的可靠性，设计对比试验来分析单向航道内的船舶减速问题。试验采取控制变量法，参数设置见表1，对3个船舶减速影响因子设置3组试验，每组试验将一个参数作为变量，其他变量取区间中间值。对于非影响因子，本次试验中取船舶安全间距D=1 200 m,船舶速度分布均值vmean=10 kn,仿真模拟时长T=300 d。试验过程中，每组试验中试验变量以一定步长改变取值，从而观测试验变量的变化对试验结果的影响。当试验变量取某一值时，由于模拟时长一定，其仿真结果会有一定偶然性，因此对于单次试验，采用蒙特卡洛方法，重复进行每次试验，试验结果以多次试验的均值来表示。

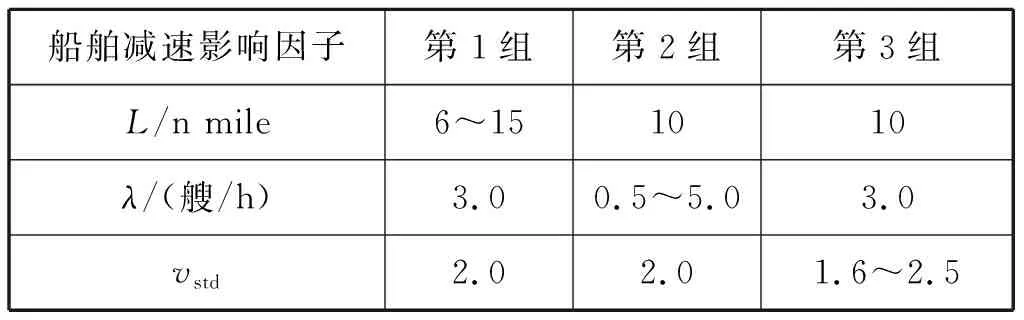
表1 试验参数设置

3.2 仿真试验结果及船舶减速概率模型验证

根据设计的3组试验，可得到试验结果见图3～图5。图3～图5中曲线显示的是船舶减速概率随船舶减速影响参数的变化关系，横坐标表示不同的船舶减速影响参数，纵坐标为船舶减速概率。仿真试验结果采用2种方案统计:一条曲线统计在整个仿真时间内所有发生减速的船舶数目与总船舶数目的比值，该曲线反映的是在试验条件下航道内的船舶减速状况；另一条曲线在统计结果时不计入因船舶减速连锁效应影响下的减速船舶，该曲线用来验证船舶减速概率模型的精度。从图3～图5中可知:3艘船舶减速影响因子与船舶减速概率相关性较好，其取值的增加都会使航道内发生减速的船舶比例增大。

对比仿真试验结果与模型计算结果，当航道长度<9 n mile，船舶到达率<2.5艘/h或船舶速度标准差<1.8 h时，试验结果与模型计算结果基本保持一致。当3个参数取值超过这一范围时，两者结果出现分歧，分析其原因为航道内单一船舶减速造成船舶连续减速，即航道内发生船舶减速连锁现象。在进行仿真试验时，不统计这一影响会造成船舶减速数量，得到的试验结果与模型计算结果基本一致，因此模型能够准确反映航道在正常通航状态下的船舶减速概率。

对于航道内船舶连续减速现象，结合第1.2节的分析，当航道内出现明显的减速连锁效应时，航道通航能力受到的影响是不可接受的。因此，航道长度9 n mile、船舶到达率2.5艘/h、船舶速度标准差1.8为航道保持正常通航状态的临界值。航道长度为航道固有属性，而船舶到达率及船舶速度差异性是基本可控的，据此可对航道内船舶交通进行一定控制，保障航道通航能力。

4 结束语

在船舶减速过程进行理论分析与数学计算基础上，建立船舶减速概率模型，实现对航道内船舶减速过程的定量描述,通过仿真试验对船舶减速概率模型进行验证。试验结果表明，概率模型能反映航道内船舶的减速概率。比较模型计算的结果与仿真结果，找出航道船舶减速产生连锁过程的临界点，而船舶减速连锁过程严重影响航道的通航能力。根据结果图中的临界点，可控制船舶到达率及船舶速度分布标准差，在临界范围内来降低船舶减速连锁效应的影响。