PCA算法在酒店推荐系统中的应用研究
刘淑英 邹燕飞 唐云凯 李依桥 赵子慧

摘 要:目前我们使用的酒店推荐系统中,会出现用户评分数据极端稀疏,矩阵的稀疏性导致推荐算法在相似性计算时存在较大误差,进而导致最近邻居选择的不准确,从而影响推荐质量。针对此问题,我们通过对评分矩阵采用PCA降维的方法,降低评分矩阵的稀疏性,保留了最能代表用户兴趣的维数,使得相似性计算更加准确,保证了最近邻居选择的准确性,从而提高了推荐质量。
关键词:机器学习;PCA算法;酒店推荐系统;降维
中图分类号:TP391.9 文献标识码:A 文章编号:1671-2064(2019)22-0051-02
0 引言
在信息技术和互联网蓬勃发展的今天,大量的数据使人们从信息贫乏的时代走到了信息过载的时代,面对大量的信息,人们获取到对自己有用的信息是非常慢[1]。因此,我们需要将信息进行过滤,找到有用的信息,从而使对数据的研究更加简单方便,这样过滤信息的能力就变成了评价一个系统的重要的条件[2]。PCA算法能够实现数据有效降维,并且可以利用特征值对原始指标进行分类,实现特征的准确提取。
1 PCA算法
PCA算法即主成分分析法(principal component analysis),用于数据降维,是以“信息”损失较小的为前提,将高维的数据转换到低维,这样就可以减小计算量[3]。它可以把一个确定事物的特征提取出来,舍掉没有特点的特征值,提取事物的本质因素,使复杂的问题简单化。
PCA算法的主旨思想就是通过对大量数据进行一系列的计算后,将高维度的数据降为低维度數据,应用于无监督学习。得到的低维将加快模型训练的速度,低维特征具有更好的可视化特性。此外,数据降维将导致某些信息丢失。通常我们可以设置一个丢失阈值来控制信息丢失[4-5]。PCA算法的计算过程如下:
设原始样本集为X,其有m个样本,每个样本有n个特征维度,可以用式(1)表示为:
(1)
接下来,我们对每个特征去均值化(即均值零化),计算公式为:
(2)
然后,我们通过计算协方差矩阵,计算公式为:
(3)
将特征向量按特征值的大小排序,组成矩阵u=[u1 u2 … un],则特征向量u1为主特征向量(对应的特征值最大),u2为次特征向量,以此类推。对于特征值越大的特征向量,样本集在该方向上的变化越大。对于由特征向量组成的矩阵我们称为特征矩阵,特征矩阵是一个正交矩阵,即满足uTu=uuT=I。
PCA算法非常巧妙地利用协方差矩阵来计算出样本集在不同方向上的分散程度,利用方差最大的方向作为样本集的主方向。PCA算法为我们提供了一种处理大量数据便捷快速的方法,在这个信息过量,发展速度迅速的时代,可以为我们提高工作学习以及生活的效率。
当样本数据量大,维度高时,PCA算法是非常有效的一种降维方法,它能起到的作用有两个:一个是节约存储空间,当数据量过多时,通过减少减少几个维度就可以节约很多空间;另一个是提供计算的速度,将数据降维后,无论是样本数据训练时,还有对新数据做出响应时,速度都会大幅提高。
2 模型实现
PCA算法的主要过程是首先构建一个示例矩阵通过使用样本集和特性,然后利用样本集,计算协方差矩阵,然后根据协方差矩阵的特征值和特征向量,并保留最大的前k个特征值的特征向量作为新维方向。将原始样本集转换为新的空间维度。
2.1 数据的采集
本文用到的样本数据集为两类,第一类样本数据为行为100000,列为5。100000表示的是用户的数量,5表示有5种类型的酒店。即100000用户对酒店在5个维度的侧重点的评分,这5个维度分别为用户酒店的浏览量,访客数,下单数,成交数,成交金额。第二类样本数据集为行为5,列为100。5表示样本,100表示的是特征点,5个维度同样代表的是浏览量,访客数,下单数,成交数,成交金额等。即第二类样本数据集为100个酒店在5个维度的评分。
使用矩阵运算,将两类样本数据集相乘,生成顾客对酒店的评分,其具体实现代码为:
hotelRating=pd.DataFrame(generators.dot(hotelcomp),index=[‘c%.6d%i for i in range(customerNum)],columns=[‘hotel_%.3d%j for j in range(100)]).astype(int)
print(hotelRating)
2.2 数据的预处理
计算样本集的平均值,再用样本集减去平均值并且除以其标准差,最后将数据进行归一化处理。其实现代码为:
def normalize(s):
if s.std()>1e-6:
return(s-s.mean())*s.std()**(-1)
else:
return (s-s.mean())
hotelRating_norm=hotelRating.apply(normalize)
2.3 模型训练
PCA算法的计算过程为:
(1)数据中心化,去均值。
(2)求解协方差矩阵。
(3)利用特征值分解/奇异值分解,求解特征值以及特征向量。
(4)利用特征向量构造投影矩阵。
首先,计算协方差矩阵,然后进行奇异值分解,PCA算法就是对协方差矩阵做特征值分解,我们使用奇异值分解来分解矩阵。其具体实现代码为:
u,s,v=np.linalg.svd(hotelRating_norm_corr)
print(‘u\n{}.format(u))
在实现的过程中,我们使用奇异值分解矩阵,使用SVD分解特征值,降低问题复杂性,奇异值分解,就是将一个矩阵通过运算分解为三个矩阵。即A=U*S*V,其中U和V均是正交矩阵,S为对角矩阵。相对于PCA特征值分解,奇异值分解可处理的不只是协方差矩阵(方阵),还可以直接处理数据。
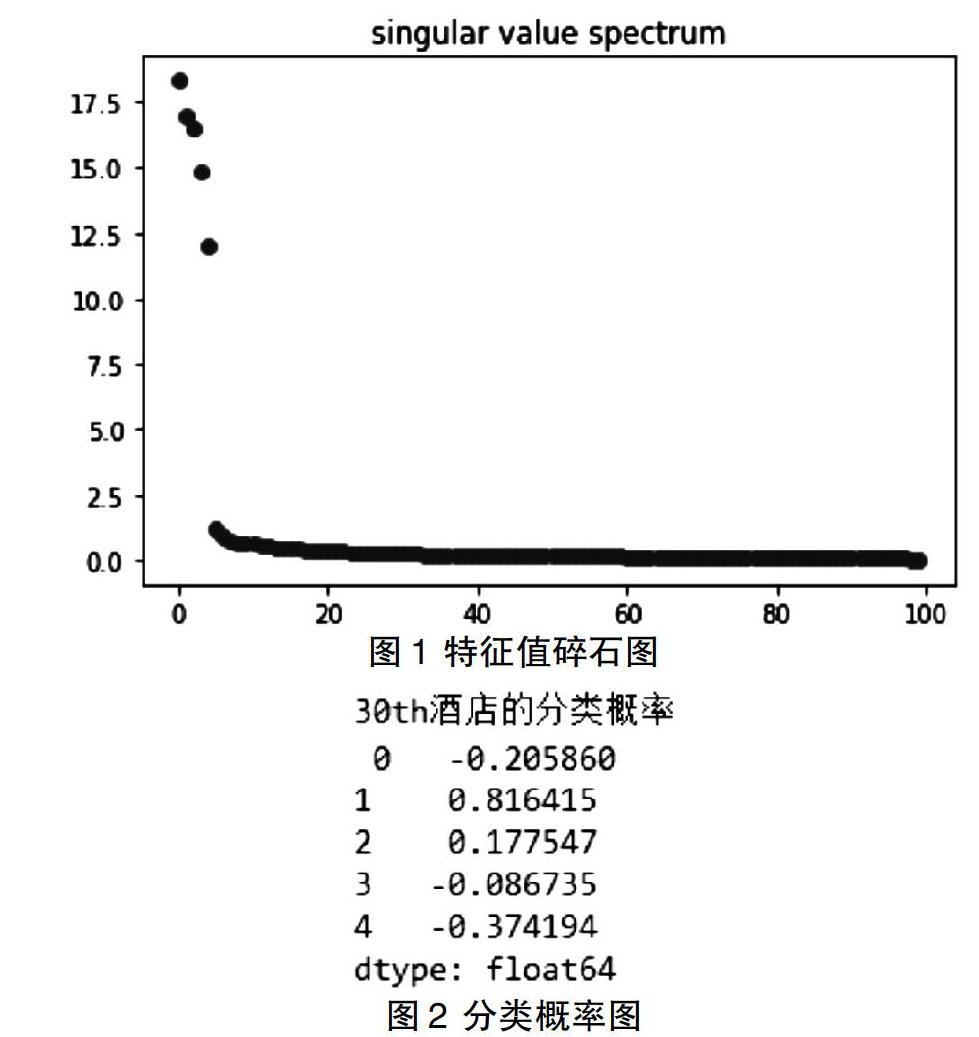
然后通过对数据的描绘,最后得到特征值碎石图,如图1所示。
根据碎石图1可知,X轴为成分数,Y轴为特征值,在第五个之后变得平缓,可得知我们可提取五个主成分,实现了PCA数据降维。
最后我们进行获取分类评分。根据分析协方差矩阵中100个样本和100个特征点的相似度,找出与每个特征点相似的样本,得到特征值。选出明显大的前k个特征值,舍去小的特征值。我们可以通过样本集特征提取最高的5个主成分。截取SVD维度来确定酒店相似度,具体实现代码为:
u_short=u[:,:5] v_short=v[:5,:] s_short=s[:5]
print(‘u,s,v,short{}.format(u_short,v_short,s_short))
該程序最终会得到一个行为100,列为5的矩阵,即100个酒店在前5个主特征值得评分。然后我们计算出指定酒店在各分类评分。首先获取样本集中的最高成分,与检索出的30号酒店的用户评分相乘。其具体实现代码为:
top_component=hotelRating_norm.dot(u_short).dot(np.diag(np.power(s_short,-0.5)))
hotel_ind = 30
rating=hotelRating_norm.loc[:,‘hotel_%.3d% hotel_ind]
print ("classification of the dth hotel"hotel_ind,
top_component.T.dot(rating)/customerNum)
该程序的运行结果如图2所示。
根据图2可以看出30号酒店与第1个分类评分最高,第3个分类的评分最低。用户可以根据自身需求选择是否入住30号酒店。
3 结语
通过用PCA算法实现简单的酒店推荐系统,在实际研究中,PCA算法是不能完全的到样本集的分类的,还要结合SVD奇异值分解获得样本集的特征值。PCA算法非常巧妙地利用协方差矩阵来计算出样本集在不同方向上的分散程度,利用方差最大的方向作为样本集的主方向。通过对该PCA算法在酒店推荐系统中的应用研究,实验结果表明:该酒店推荐算法具有较高的准确度和覆盖度。
参考文献
[1] Justiawan.Riyanto Sigit,Zainal Arief.Tooth Color Detection Using PCA and KNN Classifier Algorithm Based on Color Moment[J].Emitter:International Journal of Engineering Technology,2017,5(1):316-325.
[2] Yan Wang.An Advanced AOI-Cast Algorithm Based on PCA[J].Advanced Materials Research,2014,3227(945):1-2.
[3] 易旺.酒店搜索推荐的设计与分析[D].武汉:华中科技大学,2013.
[4] 刘艳.基于协同过滤的酒店推荐系统研究与实现[D].成都:电子科技大学,2011.
[5] 谢佩,吴小俊.分块多线性主成分分析及其在人脸识别中的应用研究[J].计算机科学,2015,42(03):274-279.

