基于HOG特征的显微镜自动对焦算法研究
马海波, 张鹏程, 张 权, 刘 瑜, 桂志国
(中北大学 生物医学成像与影像大数据山西省重点实验室, 山西 太原 030051)
随着光学技术的不断发展, 运用于图像采集的光学设备也越来越多[1-2]. 光学显微镜作为一种用途十分广泛的图像采集设备, 已成功应用于医疗病理辅助诊断、 农业害虫害防治、 环保污染物检测等领域. 显微图像的清晰程度在很大程度上影响着相关研究, 因此显微图像的清晰度判断引起了人们的广泛关注[3-4].
显微镜成像功能实现离不开自动对焦技术[5-6], 显微镜拍照时总会有一个最佳成像位置, 而显微镜平台由于自身工艺问题或使用时间太长会造成一定程度的倾斜, 容易使显微镜系统在拍照时偏离最佳位置, 图像就会变得模糊, 直接影响着后续的图像处理和相关研究, 甚至会造成研究人员的误判, 而自动对焦技术可以有效避免这种问题发生. 杨斯涵[7]提出的基于边缘特征的图像清晰度评价算法通过对当前帧图像的判断即可得到其与主观清晰度对应的参量, 但当图像背景复杂, 目标物体又很小时易受噪声影响, 该算法评价参数稳健性差. 对此很多学者作了大量研究: 吕美妮[8]等人提出的对焦算法能够选取内容丰富的子块作为聚焦窗口, 且评价函数抗噪性强; 薛万勋[9]等人提出的结合点锐度和平方梯度的图像清晰度评价算法, 具有很好的抗噪性; 张丰收[10]等人提出一种改进的Sobel梯度对焦算法, 能够很好地抑制噪声; 李郁峰[11]等人提出的灰度差分聚焦评价函数, 能有效滤除噪声, 增强稳定性.
本文提出了一种将HOG特征与拉普拉斯梯度相结合来判断图像最佳清晰度的算法, 对图像清晰度判断准确率高, 运行速度快, 鲁棒性好, 是实现显微镜自动对焦的前提, 在动态目标跟踪系统中具有重要的应用价值, 实验证明本算法在显微镜平台存在轻微倾斜时依旧有效.
1 显微镜自动对焦
1.1 显微镜自动对焦系统
显微镜系统的自动对焦通过运动控制系统控制载物平台移动, 调整物体与显微镜头间的距离, 使所成图像达到最清晰的效果, 在此过程中找到使图像清晰度最佳的位置即为对焦位置.
显微镜的自动对焦可分为传统的测距对焦法和基于数字图像处理对焦法[12-14], 利用测距对焦对机械的精度要求很高, 且对焦精度效率差, 而基于数字图像处理对焦算法是利用某种评价函数对图像质量做出客观评价, 从而判断当前图像是否清晰. 显微镜所成图像最清晰位置只有一个, 在这一位置前或后都会造成图像模糊, 图像的清晰度与镜头距物体距离大致成图 1 所示曲线.
显微镜自动对焦系统如图 2 所示, 由光学显微镜、 CCD相机、 计算机系统、 显微镜平台运动控制系统等组成. 计算机系统发送命令控制平台移动, 使载物台XYZ3轴精确定位, 通过图像清晰度评价算法完成对图像清晰度的评价, 实现自动对焦.

图 1 图像清晰度变化图Fig.1 Image sharpness change chart

图 2 自动对焦系统示意图Fig.2 Schematic diagram of autofocus system
1.2 显微镜自动对焦原理
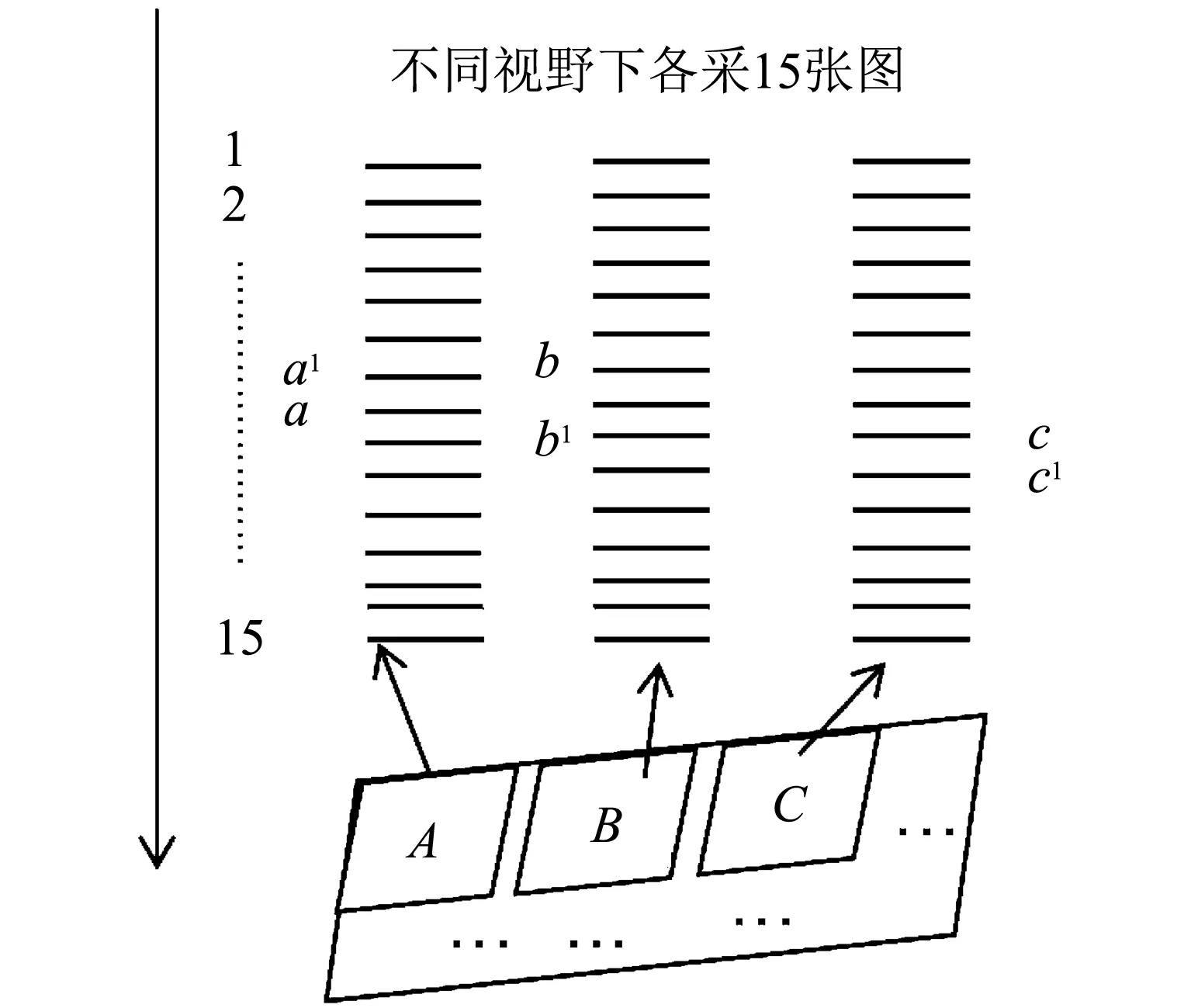
图 3 自动对焦系统原理图Fig.3 Autofocus schematic diagram
显微镜的自动对焦实现需要先人工找到一个较清晰的位置(人工对焦点为采集中心, 在中心点处采集一幅图像, 上下各7幅, 共15幅图像)执行图像清晰度算法得到最清晰图片结果, 得到与之对应的显微平台Z轴位置, 并将此位置作为下一个视野的拍摄中心. 如图 3 所示, 控制平台移动, 使玻片左上角A区域移动到显微镜视野下, 先手动找一个较清晰的位置a, 在此位置及其上下各7个位置拍摄图像, 运用图像清晰度评价算法找到最清晰的图像位置a1, 并记录此时平台Z轴位置. 保持Z轴位置不变即位置b, 在XY平面内移动载物台使玻片下区域B移动到显微镜视野下, 继续运用图像清晰度评价算法, 由于平台倾斜等原因会使B区域焦点下移到b1位置, 重复上面步骤完成对整个玻片的遍历. 这样即使平台出现倾斜造成玻片与显微镜并非完全垂直, 理想的自动对焦算法也可以自动调节高度, 依然能使拍摄的图像最清晰.
2 基于边缘特征图像清晰度评价算法
文献[7]提出图像的清晰度可以由其边缘来判断, 图像的灰度级突变越大, 图像边缘特征越明显, 图像越清晰, 其目标物体与背景边缘越锐利, 反之图像越模糊. 图像的梯度可以很好地反应图像中目标物体边缘灰度与其背景灰度之间的过渡, 利用式(1)求图像梯度
(1)
式中:d(x,y)表示图像在点(x,y)处的梯度;f(x,y)为图像在点(x,y)处的灰度值. 对图像求完梯度后, 在梯度图像中选取大小为1×5的窗口, 分别在0°, 45°, 90°, 135°方向上滑动, 求得窗口内5个梯度值总和, 利用式(2)计算每个像素点在以上4个方向上的值并取最大值.
S0°=d(x-2,y)+d(x-1,y)+d(x,y)+d(x+1,y)+d(x+2,y),
S90°=d(x,y-2)+d(x,y-1)+d(x,y)+d(x,y+1)+d(x,y+2),
S45°=d(x-2,y+2)+d(x-1,y+1)+d(x,y)+d(x+1,y-1)+d(x+2,y-2),
S135°=d(x-2,y-2)+d(x-1,y-1)+d(x,y+2)+d(x+1,y+1)+d(x+2,y+2).
(2)
基于边缘特征图像清晰度评价算法的实现具体步骤为:
1) 根据式(1)求图像梯度, 利用式(2)求梯度最大的图像边缘位置及方向;
2) 在具有最大梯度的位置沿边缘法向取7个点, 记其灰度值为fi,i=0,1,…,6, 并求得最大灰度与最小灰度差Fmax;
3) 在这7个点间取6个梯度di,i=0,1,…,5, 设F为某一固定阈值. 若Fmax≥F, 则存在边缘, 否则不存在;
4) 当有边缘存在时, 取6个梯度中位于中间的4个di,i=1,2,…,4, 找到其最大值dmax=max(d1,d2,d3,d4);
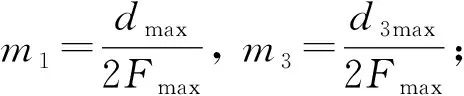
6) 图像的清晰度与m1,m3成正比, 当m1,m3分别大于各自固定阈值则图像较清晰;
7) 比较15张图像的m1值, 找到m1值最大和次大的两张图像, 再比较这两张图像对应的m3值大小,m3值大的那张图像最清晰, 即对焦位置图像.
图 4 为不同视野下的4组图像, 每个视野取15张图像, 图 4 只列出每组清晰程度不同的4张. 对每组图像运用边缘特征图像清晰度算法找到最清晰的图像, 结果如图 5 所示.
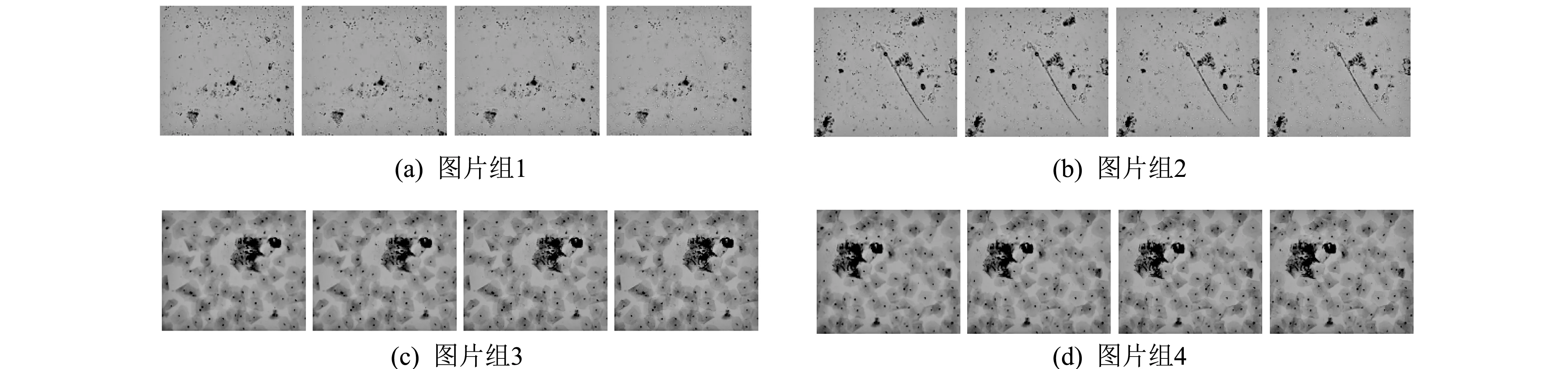
图 4 显微镜不同视野采集图Fig.4 Image from different fields of microscope
观察图 5 实验结果图, 对于图片组1和2来说, 运用边缘特征清晰度算法找到的对焦结果图, 通过肉眼观察清晰度可以接受. 但对于图片组3和4这种细胞图像, 目标物体很小, 通过肉眼观察此算法找到的对焦图片明显很模糊, 运用此算法对焦失败.

图 5 边缘特征算法结果图Fig.5 Edge feature algorithm result image
3 结合HOG特征的图像清晰度评价算法
3.1 理论基础
为了解决边缘特征图像清晰度算法存在的问题, 本文提出一种结合HOG特征的图像清晰度评价算法. HOG特征最早由Dalal[15]提出, 能够很好地描述出图像局部像素点之间的关系, 在目标物体小且背景复杂的情况下依然能对图像清晰度做出评价. 首先对同一视野下的一组图像做拉普拉斯变化并求拉普拉斯图像梯度总和sum_laplace, 找到一组图像中sum_laplace最大值和次大值及其对应的两张图像. 然后计算图像的HOG特征, 图像I(x,y)在点(x,y)处的水平梯度和垂直梯度如式(3)所示, 计算时可采用水平模板[-1,0,1]和竖直模板[-1,0,1]T与图像卷积即可得到像素点的水平与垂直方向梯度, 像素点处的梯度幅值与方向用式(4)表示.
Gx=I(x+1,y)-I(x-1,y),Gy=I(x,y+1)-I(x,y-1),
(3)

(4)
根据式(3), 式(4)求得图像的梯度大小和方向后, 将图像划分为几个小cell(单元格), 将cell梯度方向分成9个方向块, 统计落在每个方向块内像素点梯度方向的个数, 对cell中像素点基于方向的直方图投票, 投票的权值根据像素点的梯度幅值计算得出, 这样图片每个cell均有一个梯度方向直方图和梯度大小的统计, 找到每个cell中梯度大小最大的梯度值, 将图片中所有的小cell内最大梯度值加和得sum, 通过比较同一视野下15张图像的sum大小, 找到最大sum值及其对应的图像, 若此图像恰好对应之前通过laplace梯度找到的两张图像中的一张, 则认为这张图像就是最清晰的, 否则认为sum_laplace值最大的图像最清晰.
3.2 算法实现步骤
综上所述, 本文算法具体实现步骤为:
1) 对图像做拉普拉斯变化得到拉普拉斯图像, 求拉普拉斯图像梯度总和sum_laplace;
2) 计算同一视野下最大和次大的sum_laplace值, 并找到与之相对应的两张图片;
3) 计算图像的HOG特征, 将图像划分为小的单元格cell, 遍历图像统计求出每个cell内的梯度直方图和梯度大小, 找到每个cell内梯度大小的最大值max;
4) 对图片中所有cell内的最大值max求和得到sum, 找到同一视野下一组图片中sum最大的值及其对应的图片;
5) 对比sum值最大的图像是否为sum_laplace值最大或次大图像中的一张, 如果是则该sum值最大的图像即为同一视野下最清晰的, 否则sum_laplace值最大的图像最清晰.
3.3 实验结果
为验证本文算法的有效性, 对图4中4组不同视野下的图像运用本文算法进行清晰度判断. 本文算法是在Intel Corei7-4770 3.40GHz的CPU, 8GB内存的Windows7操作系统上利用Visual Studio结合OpenCV实现的, 实验结果如图 6 所示.

图 6 本文算法结果图Fig.6 Result image of algorithm in this paper
由图 6 实验结果可直观看出通过本文算法找到的4组对焦图像清晰度很高, 与图5结果对比, 图6中图片组1和2虽然很难看出两种算法的优劣, 但图片组3和4可明显看出本文算法效果更好.
为了客观比较本文算法与基于边缘特征图像清晰度评价算法的效果, 选用Tenengrad函数作为评价指标, 它是基于梯度的函数, 一幅图像越清晰, 其边缘越尖锐, 具有越大的梯度值. Tenengrad函数的原理是利用Sobel算子提取水平及垂直方向的梯度值, 图像经Sobel算子处理后的平均灰度值越大, 图像越清晰, 对应的对焦效果越好[16]. Tenengrad函数具体实现过程为:
图像I(x,y)在点(x,y)处的梯度幅值大小G(x,y)如式(5)所示, 其中Gx,Gy分别表示Sobel算子的水平核与垂直核, 符号*代表卷积. 图像I(x,y)的Tenengrad值为式(6), 其中n表示总像素数.
(5)

(6)
由式(5), 式(6)分别求出图5和图6中4张图像的Tenengrad函数值, 实验结果如表1所示. 由表1结果可知: 本文算法计算得到的对焦图像比边缘特征算法计算得到的图像Tenengrad值更大, 对于图片组1和2两种算法相差不大, 但对于图片组3和4两者相差很大, 这与肉眼直观观察完全符合. 本文算法在目标物体较小的情况下对焦效果明显优于边缘特征算法, 说明本文算法的鲁棒性更强.

表 1 算法清晰度结果
为了比较两种算法所用时间的差异, 表2统计了两种算法所用的时间. 对比表2数据可以发现: 本文算法在速度上也要优于基于边缘特征的图像清晰度评价算法.

表 2 算法耗时结果
4 结 论
针对传统的基于边缘特征图像清晰度评价算法难以实现在目标物体小, 图片背景复杂的情况下对图像清晰度做出准确判断的问题, 本文提出了一种将HOG特征与laplace图像梯度结合起来的算法, 完成多组图片的实验仿真并取得了较稳定的效果. 本文算法对图像清晰度判断准确率更高, 且运行速度更快, 是实现显微图像自动对焦的前提条件, 为后续图像处理相关工作奠定了重要基础.

