Revisit of advection-dispersion equation model with velocity-dependent dispersion in capturing tracer dynamics in single empty fractures *

Mu Wang （王沐）, Wei-dong Zhao （赵卫东）, Rhiannon Garrard , Yong Zhang , , Yong Liu （刘咏）,Jia-zhong Qian （钱家忠）

1. School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China 2. Department of Geological Sciences, University of Alabama, Tuscaloosa, USA

3. College of Mechanics and Materials, Hohai University, Nanjing 210098, China

4. School of Food and Biotechnology Engineering, Hefei University of Technology, Hefei 230009, China

Abstract: An accurate quantification of the contaminant transport through fractured media is critical for dealing with water-quality related scientific and engineering issues, where the dispersion coefficient is an important and elusive parameter for the solute transport modeling. Many previous studies show that the dispersion coefficient (D) in the standard advection-dispersion equation (ADE)model can be approximated by D = λ (where α is the dispersivity), a formula to be revisited systematically in this study by laboratory experiments and model analysis. First, a series of tracer transport experiments in single empty fractures are conducted in cases of different hydraulic gradients. Second, the tracer breakthrough curves are determined by simulations based on the ADE model,to obtain the dispersion coefficients corresponding to various fracture roughnesses and flow velocities. A varying trend of λ is analyzed under different flow conditions. Results show that although the standard ADE model cannot be used to characterize the late-time tailing of the tracer BTCs, likely due to the solute retention, this simple model can simulate most of the solute mass dynamics moving through fractures and may therefore provide information for estimating the dispersion in parsimonious models appropriate for the non-Fickian transport. The following three conclusions are drawn: (1) the peak of the breakthrough curves comes earlier with increasing the roughness, according to the ADE simulation, (2) the value of λ generally decreases as the relative roughness of the fracture increases, (3) the value of λ is approximately equal to 2.0 when the dispersion is dominated by the molecular diffusion in the smooth fracture.

Key words: Dispersion coefficient, molecular diffusion, roughness, variation trend, single fracture

Introduction

In hydrogeological sciences, the nature of the groundwater flow through fractured media is an important issue[1-3]. Yu et al.[4]investigated three different aquifer host rocks through leaching experiments with 13 trace elements under different experimental conditions, to examine the effect of the host rock mineralogy on the leachate composition, and to extract useful information about the groundwater source. Qian et al.[5]discussed the influence of the roughness and the Reynolds number on the flow through a single rough fracture and concluded that those factors did influence the flow’s friction. The solute transport in fractured media has also attracted a great deal of research attention. Wang et al.[6]developed an efficient quasi-3-D random walk particle tracking (RWPT) algorithm to simulate the solute transport through natural fractures based on a 2-D flow field generated from the modified local cubic law(MLCL). Zhou et al.[7]dealt with a coupled threedomain transport problem using mobile and immobile domains to characterize a filled single fracture and a matrix domain to characterize the rock body. Kang et al.[8]proposed a correlated continuous-time random walk (CTRW) modeling approach, as a simple yet powerful framework for characterizing the impact of the velocity distribution and correlation on the transport in fractured media. Becker and Shapiro[9]excluded the influence of the diffusion and the tough flow in the fracture solute transport, and found that the abnormal phenomenon in the breakthrough curves is caused by the anisotropy of the aperture distribution,which may be attributed to the fracture surface roughness.

The ADE model with a velocity-dependent dispersion coefficient was proposed to quantify the contaminant transport in geologic media. The solute transport in three-dimensional heterogeneous media can be quantified by the following ADE model

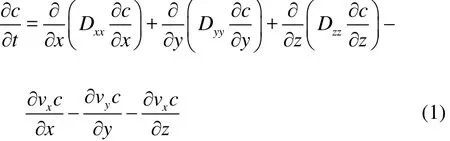
where /ct∂∂ is the concentration variation of the solute in the migration process, and the subscripts(,,)x y z denote the directions of the velocity or the dispersion. The first three items on the right side of the equation express the solute transport caused by the hydrodynamic dispersion, and the last three items express the solute transport caused by the advection.The Green’s function solution of the 1-D advectiondispersion equation (ADE) is expressed as

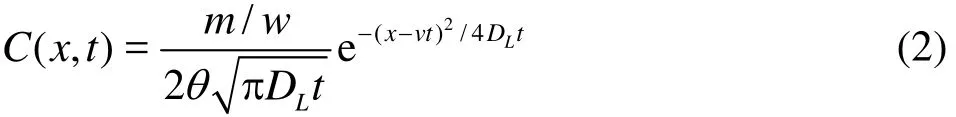
which describes a symmetric normal distribution in space at a given time, meaning that the resident concentration distribution is unimodal and it attains a peak value when = /t x v.

If (1) there is linear isothermal adsorption on the fracture surface during the solute transport, and (2) the inlet boundary has a continuous source with a constant concentration0C, then the definite solution for the solute transport process can be expressed as:

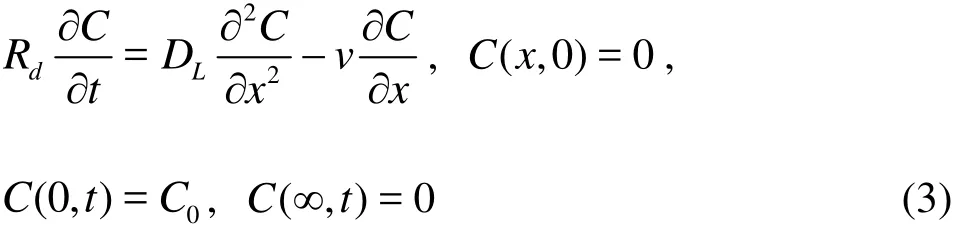
where C is the solute concentration,dR is the retardation coefficient, andLD is the longitudinal dispersion coefficient. The analytical solution of Eq.(3) is

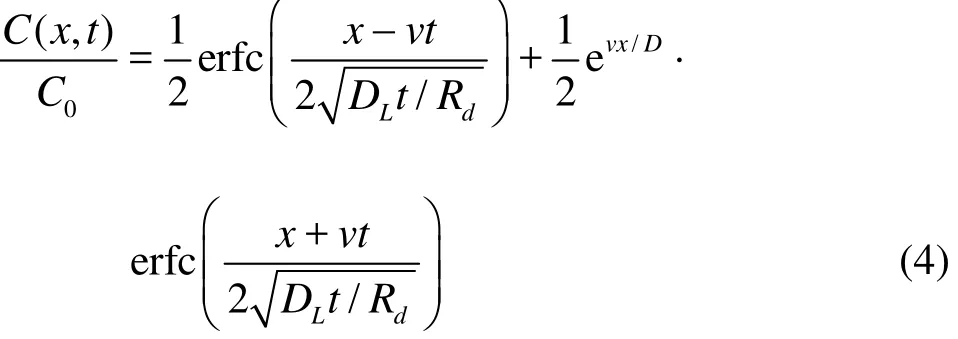
With a large enough x or t, the second item in Eq. (4) can be ignored, then one obtains

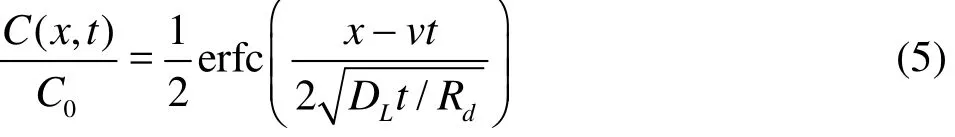
which can be simplified as

leading to

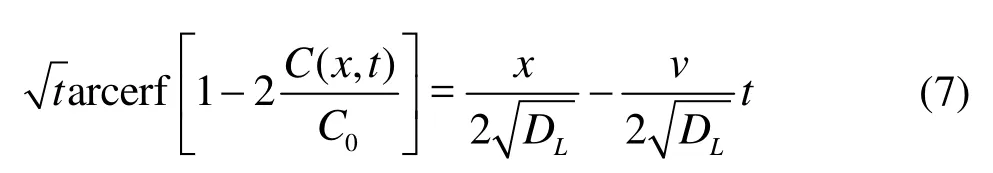
In this study, Eq. (7) is solved using the Matlab’s erfinv fu nction, to obtain a linear relationship between t and, and the dispersion coefficient can be expressed as

Parsimonious models with an effective dispersion coefficient were proposed by adding additional parameters to the standard ADE in order to simulate the transport in complex porous or fractured media with intrinsic multi-scale heterogeneity. For example, the well-known continuous time random walk (CTRW)model developed by Berkowitz et al.[10], the multi-rate mass transfer (MRMT) model developed by many researchers, including Tecklenburg et al.[11], and the fractional advection-dispersion equation (FADE)models[12], used to capture the non-Fickian or anomalous transport in natural geological media. In these stochastic models, a spatial averaged velocity and a constant dispersion coefficient are usually assumed,and the impact of the local flow velocities deviating from the mean velocity on the solute transport is captured by additional terms, such as the memory kernel in the CTRW model, the mass transfer rate coefficients combined by the capacity coefficients in the MRMT model, and the fractional index in the FADE model. The direct measurement of most of these additional parameters, however, remains a challenge. Most importantly, the effective and typically constant dispersion coefficient is not known in these complex models. Since the standard ADE model is much simpler and for the velocity-dependent dispersion coefficient, a potential mathematical formula can be used (although the exact values remain to be shown), we revisit and evaluate the standard transport model with a constant dispersion coefficient, which might shed some light to the selection of the effective dispersion coefficient in the CTRW, MRMT, or the FADE models.

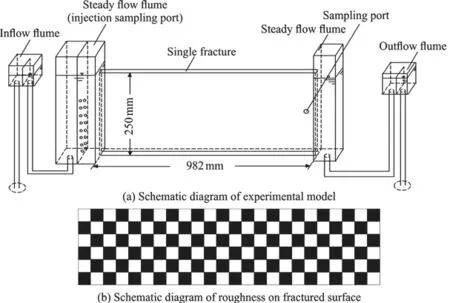
Fig. 1 Schematic diagram of experimental setup

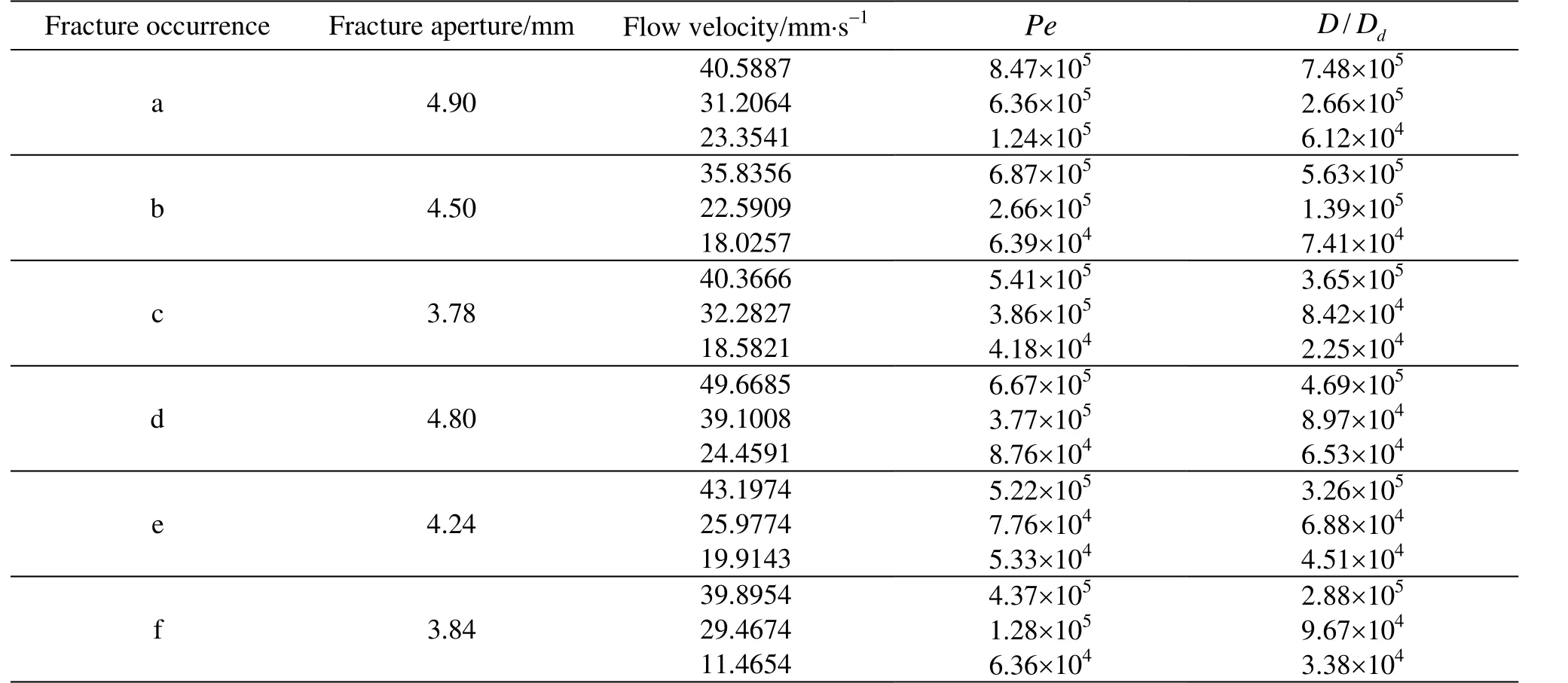
Table 1 Values of solute transport Pe and D/ Dd in different fracture situations

When moving through a porous or fractured medium, the contaminant particles can be driven by the mean flow velocity, whose spatial fluctuation (due to the local variation of hydraulic properties) can be accounted by the hydrodynamic dispersion with a coefficient D. The correlation between the dispersion coefficient D and the flow velocity v was quantitatively studied. For example, Dou et al.[13]obtained roughness scale dependence of the relationship between tracer longitudinal dispersion and Peclet number in fractures. Later, Dentz and Carrera[14]quantified the dynamic D by using a spatial moment analysis. Wang et al.[15]derived a closed-form expression for the dynamic longitudinal dispersion coefficient and analyzed the time and length scales for the distinguishing Fickian and non-Fickian transport regimes. Bear[16]built a model by a string of small units, linking each other with short passages, and he assumed that when a fluid with a certain concentration of the tracer flowed into a unit of another fluid with a different concentration, the former displaced a part of the latter fluid, to form a new kind of homogeneous fluid immediately, and this unit was called the ideal mixer. In the ideal mixer, the effect of the molecular diffusion is negligible. After many tests, he discussed the correlation between the dispersion coefficient and the flow velocity, and came up with the equation

where α is the dispersivity, v is the flow velocity,and λ is an exponent with a suggested value ranging from 1.0-2.0. Pugliese and Poulsen[17]established a set of expressions for estimating the dispersion coefficient in porous media at low velocities, taking into account the effect of porous media on the physical properties, they also came up with Eq. (8). Douglas and Stephen[18]analyzed the influence of the fracture roughness on the correlation between the dispersion coefficient and the flow velocity in a single fracture,and concluded that the value of λ was 2.0 for smooth parallel plates, and approximately 1.3 for rough plates. A systematic study is still needed to further understand the nature of the solute transport in fractured media and explore the variations of the dispersion coefficient against the fracture roughness and the flow velocities, which is the purpose of this study.

In this paper, we carry out the laboratory experiments and the model analysis to decipher the velocitydependent dispersion. We first conduct a series of hydraulic tests with different hydraulic gradients in the laboratory. The solute transport is then fitted using the ADE model, to analyze and disclose the variations of the dispersion coefficients against the fracture roughness and the flow velocity under different hydraulic conditions.

1. Experimental design

1.1 Experimental setup

The schematic diagram of the experimental setup of the flow and transport tests in a single fracture is shown in Fig. 1(a). The model is made of perspex casing with dimensions of 982 mm×250 mm×7.5 mm(length × width × height), placed horizontally. It includes three major parts: the inflow (outflow)flumes, the steady flow flumes, and the single fracture.The fracture roughness is varied by affixing rough plastic plates along the fracture walls, as shown in Fig.1(b). There are six types of fractures according to the size of plastic plates: 40 mm×40 mm×1 mm, 40 mm×40 mm×2 mm, 40 mm×40 mm×3 mm, 20 mm×20 mm×1 mm, 20 mm×20 mm×2 mm and 20 mm×20 mm×3 mm,marked with (a) through (f), respectively, as shown in Tables 1, 2. The relative roughness is the ratio of the surface relief to the fracture aperture, and the surface relief is the height of the plastic plate and the aperture value is obtained from Table 1. The water and the tracer (NaCl) flow into the fracture from the steady flow flume. The tracer samples are taken from a sampling port, and put on the fracture plate, to the right of the steady flow flume. They are then measured by a DDS-307 conductivity meter, manufactured by the Shanghai Optical Instrument Factory. The tracer concentration values are obtained by using a standard curve. All experiments are conducted with tap water.

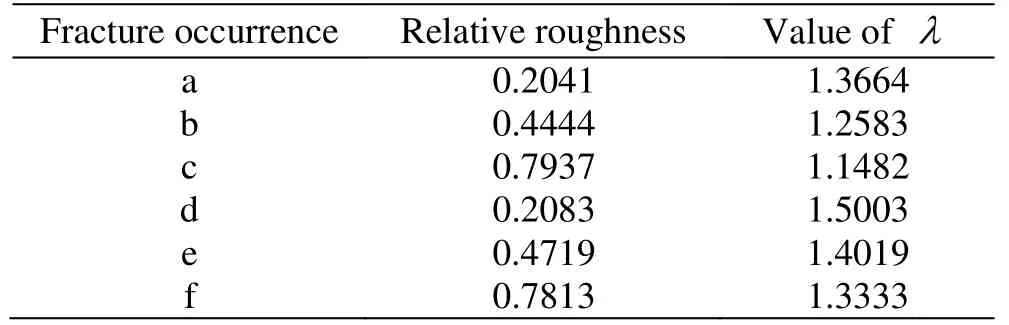
Table 2 Values of λ in different fracture situations

1.2 Experimental method

A graduated cylinder is used to gauge the steady flow velocity during the tests with errors below 2%.The height of the inflow (outflow) flumes could be moved up or down, and the water head differences are controlled by adjusting both ends of the model. The water flow is monitored to determine if it follows the Darcy’s law. The tracer conductivity is measured for the collected samples and is used to plot the breakthrough curves according to standard curve procedures. The dispersion coefficients are calculated in accordance with the standard advection-dispersion equation.

2. Results and discussions

The Peclet number, according to the diagram of the relationship between the molecular diffusion and the hydrodynamic dispersion by Bear[19]is =Pe, where v is the average velocity, b is the average aperture, anddD is the molecular diffusion coefficient. Peclet numbers calculated from the tests are listed in Table 1. The values of Pe range from, and the values ofrange fromIn the equation, the parameter ∂ is approximately equal to 0.5, m is an exponent,whose value ranges from 0 to 1.2. Our experiment points fall into the zones IV and V, as seen in Fig. 2.In these zones, the mechanical dispersion plays the major role while the effect of the molecular diffusion is negligible. In this case the dispersion coefficient can be determined as =D vλα .

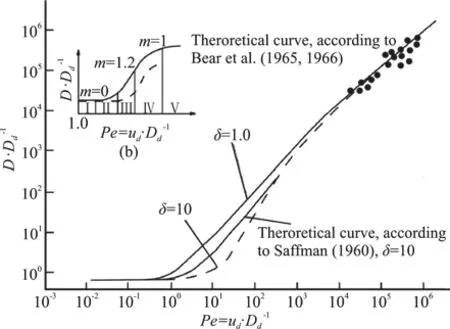
Fig. 2 Relationship between molecular diffusion and hydrodynamic dispersion

2.1 Analysis of flow condition

In this test, the heights of the inflow (outflow)flumes are adjusted and the flow velocities are calculated for different hydraulic gradients. Their relationship is shown in Fig. 3. The Darcy’s law and the Forchheimer’s formula are used to fit the experimental data. The correlation coefficient for the Forchheimer’s formula is larger than that for the Darcy’s law. In addition, the relationship between the hydraulic gradient and the velocity is nearly quadratic. Therefore,the water is regarded as obeying the non-Darcian flow.

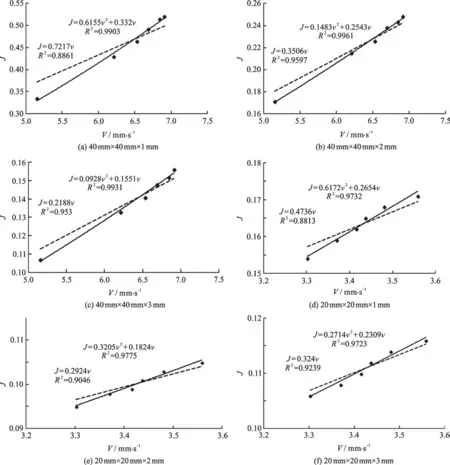
Fig. 3 Fitting curves of hydraulic gradient versus velocity in fractures of different roughness for different equations

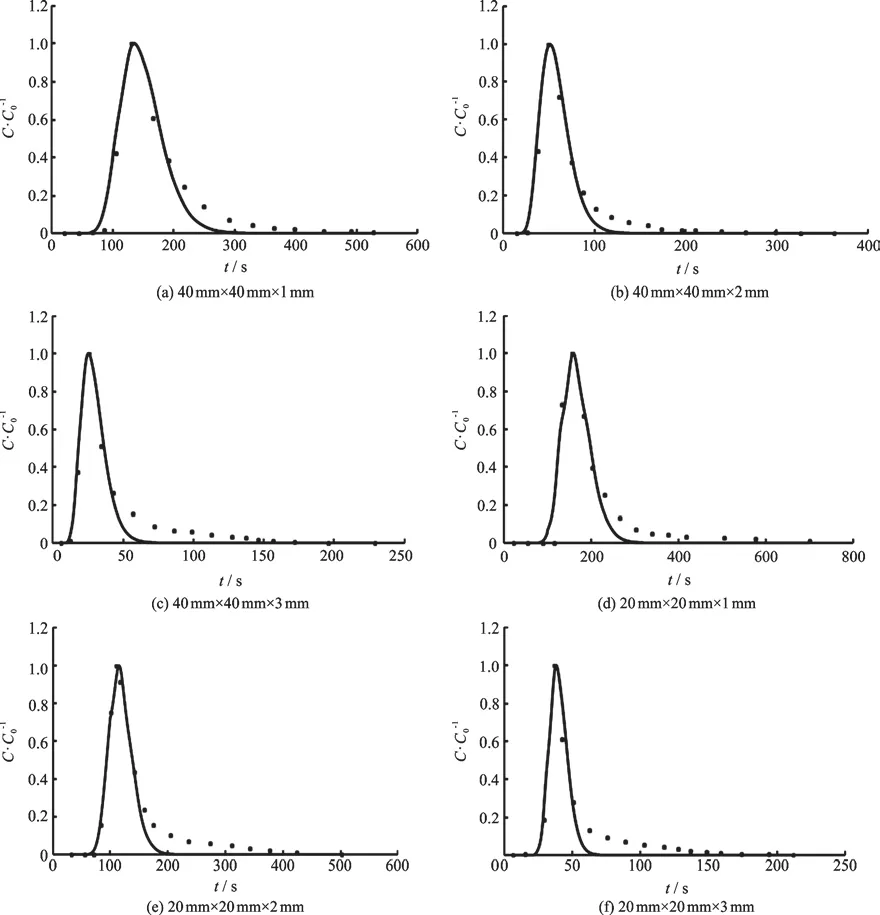
Fig. 4 Experimental data and ADE breakthrough curves at the velocity of 31.4105 mm/s

2.2 ADE model of solute transport

The NaCl is used as the tracer in this study.The tests of the solute transport are conducted with the tracer concentration values obtained according to the standard curve procedure using the conductivity values. The breakthrough curves of the solute transport through the rough-walled and smooth fractures are determined by the simulation with the ADE model,as shown in Fig. 4, Fig. 6(a).

The simple ADE model with a constant dispersion coefficient for each BTC can capture the dynamics for a majority of the solute mass moving through each fracture. In addition, the timing of the concentration peak occurs earlier as the roughness increases,as shown in Figs. 4(a)-4(c) and Figs. 4(d)-4(f). The reason might be that the channeling of the groundwater flow is enhanced as the roughness increases,and therefore, the solute transported in the channel moves relatively faster than with the average velocity.

It is worth noting that with the simple ADE model, the late-time tailing of the tracer BTC is underestimated. The delayed transport for some solute particles is one of the common characteristics of the non-Fickian transport, which is typically caused by the solute retention at zones of relatively small velocities. The retention process cannot be captured by a Fickian diffusive process with the standard ADE model, but may be efficiently simulated by stochastic models such as the CTRW, MRMT, or FADE models,where additional parameters and/or terms are designed to specifically capture the solute retention. Hence the dispersion coefficient determined in this study with the standard ADE might serve as a useful reference for the effective, typically constant dispersion coefficient in the stochastic models. We will focus on the stochastic models for the non-Fickian transport in a future study.

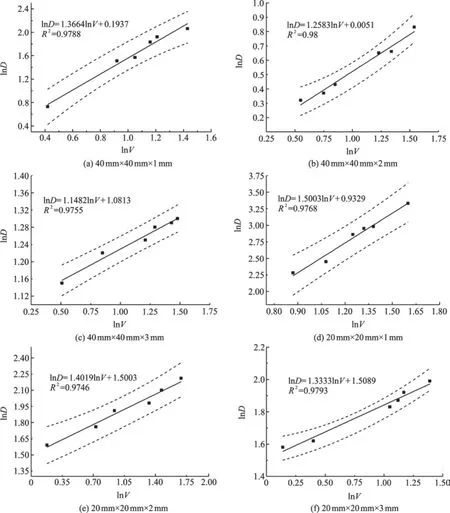
Fig. 5 Log-log plots of dispersion coefficient versus velocity in rough fractures of different roughnesses

2.3 Analysis of velocity dependence of dispersion co-efficient in rough fracture

Corresponding to the above analysis, the values of the dispersion coefficient are calculated at different flow velocities, then log-log plots of the values are drawn, as shown in Fig. 5. The values of λ obtained from the plots (a) through (f) are listed in Table 2:they range between 1.0 and 2.0, in good agreement with those in the study of porous media by Bear[16].

In addition, the rough plastic plates in the fractures (a)-(c) have the same length and width but different heights. From Table 2 it is evident that the values of λ decrease with the increase of the relative fracture roughness, and the same trend is found in the fractures (d) through (f).

2.4 Analysis of velocity dependence of dispersion co-efficient in smooth fracture

The solute transport in smooth fractures is also an important aspect in the observation. In this study,the dispersion coefficients are calculated, for different flow velocities, in a smooth fracture with a 4 mm aperture. The results are shown in Fig. 6(b). The value of λ is found to be 2.0038. Next, Pe is calculated for different flow velocities (Table 3). Detwiler and Rajaram[20]concluded that the molecular diffusion dominates the solute transport in cases of 1Pe≤ in a smooth fracture. In this study, 1Pe≤ for all cases,thus the solute transport is indeed dominated by the molecular diffusion. The results confirm the research results of Douglas et al.[18]for the dispersion coefficient, proportional to the square of the velocity for the transport dominated by the molecular diffusion in the smooth fracture.

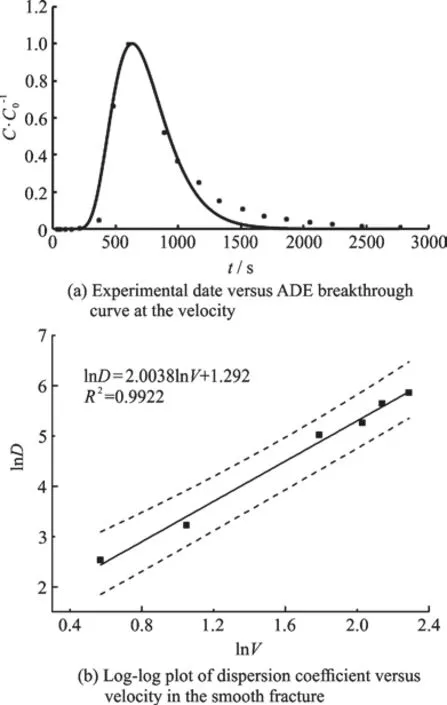
Fig. 6 Experimental results for the smooth fractures

Table 3 The Pe values versus flow velocities in smooth fracture of 4 mm aperture

3. Conclusions

In this study, the tracer transport tests are conducted for various flow velocities and fracture roughnesses. From the statistical analysis, the following conclusions can be drawn:

(1) Although the standard ADE model can not well simulate the late-time tailing in the tracer breakthrough due to the solute retention, it can capture the early arrivals and the main features of the transport that the peak of the breakthrough curve arrives earlier as the roughness in the rough-walled fracture increases. This simple model may, therefore, provide some useful information for estimating the effective and typically constant dispersion coefficient used in parsimonious, stochastic transport models designed specifically for the non-Fickian transport.

(2) The dispersion coefficient is found to be proportional to the flow velocity when the dispersion is dominated by the advection in a rough fracture. The relationship can be expressed as =D vλα (which follows the same power-law rule as that identified by many previous studies), where the experimental values of λ range from 1.1482 to 1.5003, decreasing with the increase of the relative fracture-wall roughness under non-Darcian flow conditions.

(3) The proportional relationship between the dispersion coefficients and the flow velocity is found to be stable when the dispersion is dominated by the molecular diffusion in smooth fractures, where the value of λ is approximately equal to 2.0.

Acknowledgements

This work was supported by the Key Program of Huainan Mining Group Co. LDT (Grant No. HNKYJT-JS-2010), the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (Grant No. 2013490111), the Public Welfare Geological Survey Program of Anhui Province (Grant No.2015-g-26), the Shandong Province Pilot Program of Science and Technology on Construction of Water Eco-civilization. YZ was funded by the National Science Foundation, United States (Grant Nos. DMS-1025417, DMS-1460319.