跨海大桥动力响应监测与计算

杨 帆，王少钦

(1.北京建筑大学 土木与交通工程学院，北京 100044；2.北京建筑大学 理学院，北京 100044)

近几十年来，世界各国桥梁建设快速发展，桥梁设计方法和施工技术的不断创新，促成了以斜拉桥、悬索桥为代表的大型桥梁建设突飞猛进。桥梁跨径记录不断被刷新，我国斜拉桥应用跨度已从96 m发展到接近 1 100 m[1]，并且作为世界上拥有斜拉桥数量最多的国家，全球主跨长度排名前10位的斜拉桥中，我国占据其中6席，见表1[2]。

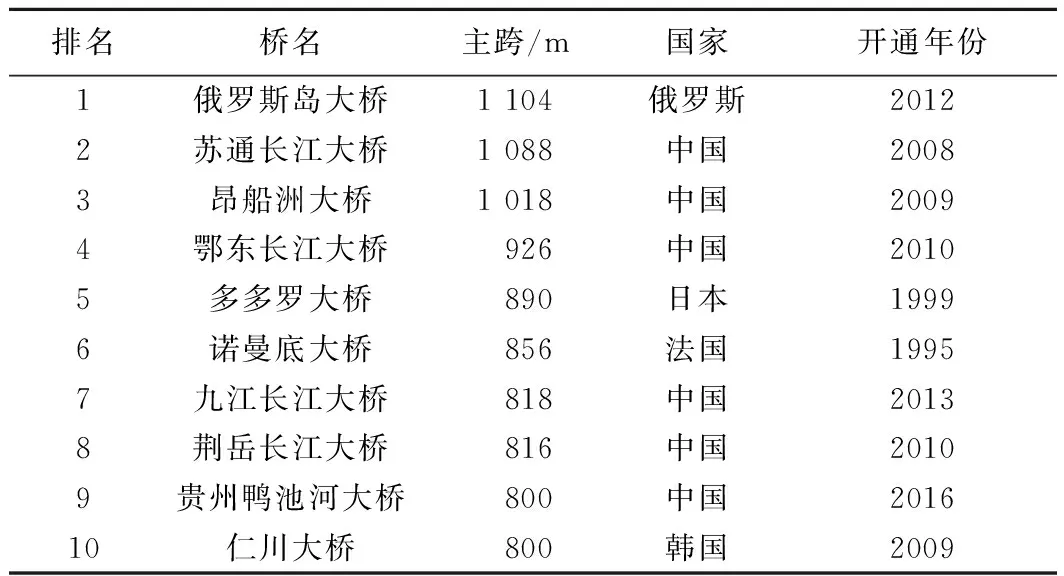
表1 世界斜拉桥主跨长度排名前十名

桥梁的使用期长达几十年、甚至上百年，桥梁结构服役过程中在荷载的长期效应、疲劳效应、材料退化、环境侵蚀及初始设计、施工过程中产生的各种不良因素的综合作用下，将不可避免地导致其强度和刚度逐渐降低、抗力衰减[3]，从而影响桥梁工程的正常及安全使用。国内外由此引发了多起桥梁安全事故：2001年宜宾南门大桥断裂，造成3车坠江，1船被毁、2人死亡、2人失踪、多人受伤，全市对外交通受阻而造成上亿元的经济损失。 2006年12月印度东部地区一座上跨铁路的大桥垮塌，造成桥下一列正在行驶的城际列车上33人死亡。2007年美国明尼苏达州的一座桥梁发生坍塌，60多辆汽车跌入密西西比河，7人死亡，至少60人受伤。另有众多桥梁出现了不同程度的性能退化，各国每年均要花费巨资用于旧桥的维修加固。桥梁的安全问题日益严峻，由此对桥梁结构进行实时的健康监测越发受到人们的重视。

利用健康监测系统对大型桥梁进行实时监测，克服了传统人工检测所不可避免的实时性差、整体性差、受检测人员数量及知识经验影响大、影响正常交通等不足之处[4]，成为保障桥梁结构可靠性、安全性和耐久性，实时掌握桥梁健康状况的有效手段。桥梁健康监测本身也是对桥梁的足尺试验，并且试验项目全面，测试数据丰富，能够得到真实桥梁在真实荷载和真实环境下的各种响应。其得到的大量长期监测数据将对完善大型桥梁结构的设计理论以及进行大型桥梁结构的相关科学研究具有极为重要的意义[3]，受到许多桥梁专家学者广泛关注。

东南大学的李爱群团队对结构健康监测策略和传感器优化布设进行了研究，据此设计了润扬长江大桥健康监测系统[5]。同济大学的孙利民团队致力于研究桥梁健康检测新技术与大型桥梁管理系统，同时参与了徐浦大桥、东海大桥、苏通大桥的桥梁健康监测设计与建设[6]。香港理工大学的倪一清团队致力于研究桥梁结构健康监测的推广应用，参与了国内多座大跨度桥梁健康监测系统的设计和建设[7]。哈尔滨工业大学的欧进萍、李惠团队开展了斜拉桥健康监测系统的设计与实现的研究，参与建立了滨州黄河公路大桥和哈尔滨松花江大桥的桥梁健康监测系统[8-9]。

本文对一座跨海大桥的健康监测系统做了介绍，并利用实测数据与数值模拟试验所得结果进行对比的方法验证了模拟试验的有效性，最后进一步利用有限元模型分析该桥在不同工况下的响应规律。

1 跨海大桥简介

1.1 工程概述

跨海大桥为分幅叠合梁公路斜拉桥，全长800 m，主跨为400 m，两侧有辅跨130 m和边跨70 m对称布置。三柱式门型桥塔，索塔高158 m，全桥共有288根斜拉索，设计行车速度100 km/h，设计基准期100年，地震基本烈度为Ⅶ度。其主桥总体布置和单幅主梁标准横断面如图1所示。

图1 大桥示意

1.2 桥梁监测系统

为了保障该跨海大桥的运营安全，该桥设置了安全监测系统，通过实时监测桥梁的运营状态评估桥梁的安全度，为桥梁的管理、养护提供科学依据。

该桥监测系统的监测项目主要包括主梁风荷载、索塔风荷载、主梁震动、斜拉索震动、地震动、索塔震动、防撞墩震动、GPS、动态称重、主梁温湿度、索塔温湿度、主梁变形、降雨量、梁端位移、结构应力、结构温度等。监测系统由传感器、调理器、采集服务器、数据处理器、数据库、IIS等部分构成。桥梁的各项监测数据的获取及应用流程如图2所示。

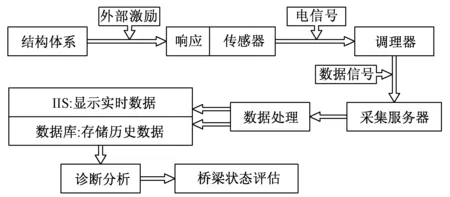
图2 监测数据的获取流程

1.3 有限元模型

利用ANSYS有限元分析软件，通过编写APDL命令流的方式进行斜拉桥的建模、计算及数据后处理[10]，斜拉桥的主梁、桥塔及桥墩采用Beam 4单元进行模拟，拉索采用Link 10单元模拟。

对斜拉桥进行模态分析，得到主梁的前10阶自振频率及振型列于表2。

表2 斜拉桥自振模态

2 桥梁荷载

2.1 车辆荷载

汽车模型采用文献[11]中箱式货车的参数,简化为前39.14 kN、后34.26 kN相距5.6 m的移动集中力。汽车荷载列中的车距根据《中华人民共和国道路交通安全法实施条例》中规定的安全车距并结合实际情况采取0.5的折减系数进行取值，在计算中取25 m。根据桥梁实际情况并结合相关规范[12]，汽车荷载的横向折减系数取0.78，纵向折减系数取0.96。汽车荷载的布置情况如图3所示。

图3 汽车荷载布置示意(单位：m)

2.2 风荷载

风荷载由跨海大桥主跨跨中处风速监测仪测得的某时段风速样本计算所得，该时间段内平均风速为7.27 m/s。为了研究多种不同风速条件下斜拉桥的振动响应，需按照规范中的风速谱进行不同平均风速下的风荷载时程数值模拟。本文采用Cao等提出的一种快速谱分析法[13]，其基本假定为：桥面沿水平方向是等高程的，平均风速和风谱沿桥面不变，任意2个模拟风速点之间的距离相等，桥梁第i个节点的纵向和垂直方向风分量的时程h(t)和v(t)可以由下式产生

式中：Δu为谱线之间的频率间隔；N为频率分量的总数；i=1,2，…，m；m为主梁模拟风速点的总数；φnj是0～2π 之间均匀分布的随机变量；G(u)是风速点之间的相关系数矩阵；Sh(u)和Sv(u)分别为水平和竖直风速自功率谱，按照我国JTG/T D60-01—2004《公路桥梁抗风设计规范》的规定进行计算。

对该跨海大桥主梁上的76个节点处的风速进行模拟时，风速节点间距取值与梁段长度保持一致，为10.5 m。

3 桥梁振动响应分析

为了方便输出，在桥梁主跨跨中、1/4跨及两侧辅跨跨中分别定义A,B,C,D和E点如图4所示。

图4 振动响应输出节点图示

首先模拟计算由3列、48排共144辆汽车组成的连续车队荷载列以80 km/h车速在桥上行驶时的桥梁动力响应。将在平均风速为7.27 m/s时段内实测的主跨跨中A点的竖向及横向加速度数据与在前述模拟车辆及相同风荷载共同作用下所得的相应值进行对比，如图5所示。可知模拟所得加速度曲线与桥梁监测系统实测数据振动形式相同，曲线波动范围很接近，说明该数值模拟试验有较好的可信度，能够较为准确地反应该跨海大桥的动力响应，对该桥其他工况下的响应规律做进一步的研究。

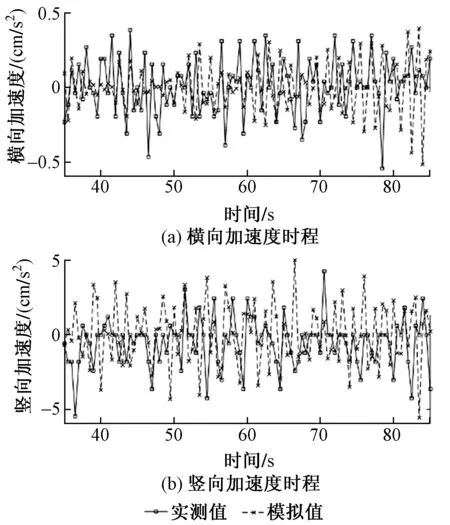
图5 实测与模拟桥梁跨中节点加速度时程曲线对比

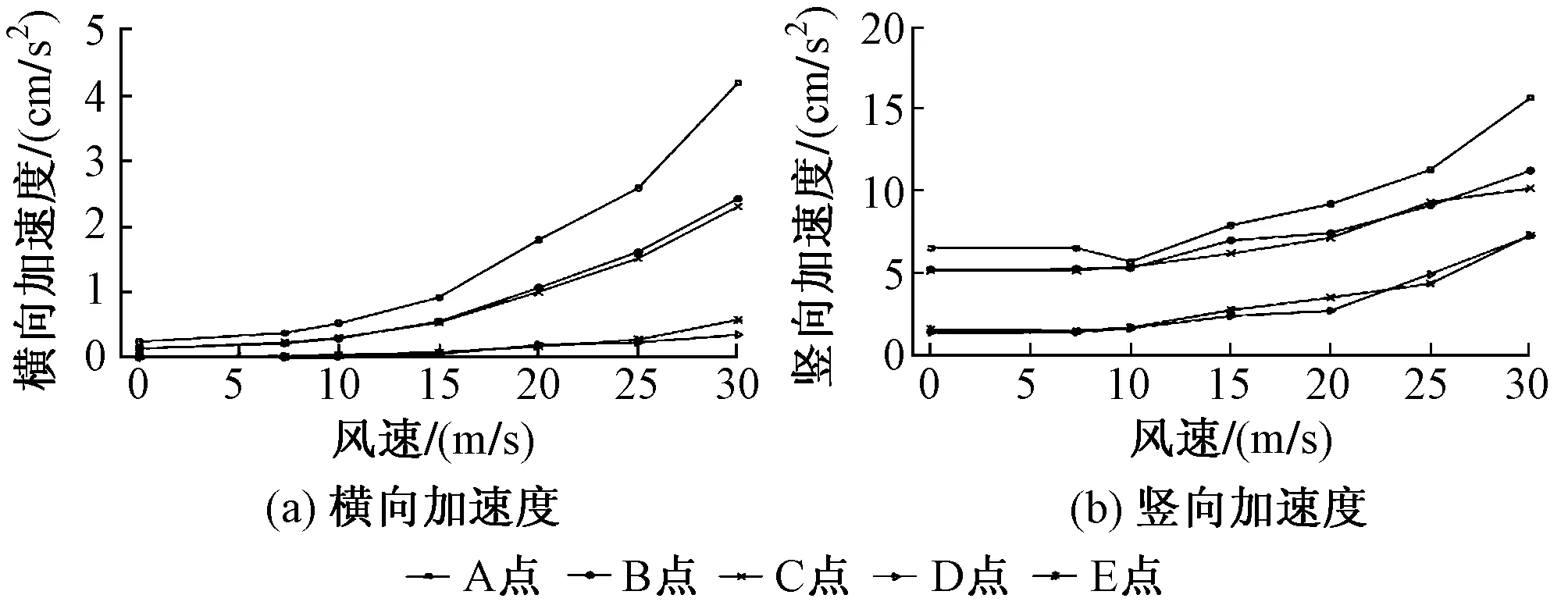
图6 桥梁各节点加速度极值随风速变化曲线

分别计算在车速为80 km/h时平均风速分别由0增加至30 m/s时桥梁的振动响应，斜拉桥各节点的横向、竖向振动加速度极值的变化趋势见图6。由图可知桥梁振动加速度极值随着风速的增加而明显增大，且竖向振动加速度相较于横向振动加速度的增幅更大，证明该斜拉桥对风荷载的敏感性。

斜拉桥各节点的横向位移极值随风速变化曲线如图7所示。可知，主跨跨中A节点比其他各点的横向位移大出很多，A点处的横向位移极值随风速变化斜率较大，说明斜拉桥主跨横向位移对风荷载较为敏感，与桥梁模态分析结果一致。

图7 桥梁各节点横向位移极值随风速变化曲线

当风速均值取7.27 m/s时，汽车荷载分别以40，60，80，100，120 km/h 5种车速过桥的情况下，桥梁A，B点处振动响应随车速变化趋势的模拟计算结果如图8 所示。可知，车速变化对桥梁横向位移的影响并不大，而对跨中节点的竖向位移影响较为明显，当车速在40～100 km/h时，跨中最大竖向位移几乎无变化，当车速超过100 km/h时最大位移明显增加。

图8 A,B点横、竖向位移极值随车速变化曲线

4 结论

1)本文以一座跨海大桥为工程背景，介绍了该桥健康监测系统的概况。建立了有限元分析模型，利用实测数据与数值模拟计算所得结果进行对比，验证了模型的有效性。以此为基础利用有限元模型计算了该桥在不同工况下的响应规律。

2)通过计算得出该斜拉桥自振频率较低，对风荷载作用较敏感。未考虑风荷载时，主梁各点的横向位移和横向加速度均很小，几乎为零，考虑风荷载作用后主梁的横向位移随着风速的增大而显著增大，因此主梁的横向位移响应主要由风荷载控制。

3)车速的变化对桥梁的横向位移影响不大，但当车速超过100 km/h时跨中节点最大竖向位移明显增加，由此验证了该跨海大桥设计行车速度的合理性。