3T1R并联机构降耦设计与分析

2019-01-05 07:45朱小蓉沈惠平杨廷力

农业机械学报 2018年12期

朱小蓉胡旸沈惠平杨廷力朱伟

(常州大学机械工程学院，常州 213164)

0 引言

3T1R并联机构由于能实现沿x、y、z轴的平动和绕固定轴(通常为z轴)的转动，可用于分拣、包装、码垛、装配等操作，在工业中得到大量应用。最初的3T1R并联机构是在3-DOF Delta机器人[1]的基础上加装中间UPU支链以实现绕z轴的独立转动。在此之后，提出了一系列由4支链和铰接双动平台组成的3T1R并联机构[2-8]，如H4、I4、Par4、Heli4、CrossIV等；文献[9-14]提出了一类结构对称、具有4支链和刚性单动平台的3T1R并联机构。上述能实现3T1R运动的并联机构中，含铰接双动平台的机构，通过2个子动平台的相对运动和特定设计的传动装置能实现较大旋转角，最大转动范围可达[-90°,90°]，但该类机构的结构和运动学都较为复杂；而刚性单动平台3T1R机构，由于支链耦合、机构奇异性的影响，这些机构的工作空间特别是转动范围受限，且这些机构的耦合度较大(κ=2)，其运动学正解、动力学分析求解复杂。因此，为满足工程实际应用需要，还需要对解耦及大转动能力的3T1R并联机构进行更多的研究。

根据基于方位特征(Position and orientation characteristic, POC)方程的并联机构拓扑结构设计理论，文献[15]提出了3种拓扑结构降耦设计原理和方法,其中，基于运动副复合的设计方法，在降低机构耦合度的同时，使机构的结构设计、制造变得更简单，已成为并联机构拓扑结构降耦设计的一种主要方法[16-18]。

文献[19-21]提出了一种具有较好应用前景的四自由度Quadrupteron并联机构，能实现三平移和绕动平台法线的一个转动输出，但机构的耦合度较高(κ=2)，且机构的转动能力受限。本文采用基于运动副复合的设计方法，对其进行结构降耦，以得到一种自由度和末端件输出运动类型保持不变，但机构耦合度降低，且具有运动解耦的新机型。

1 降耦并联机构

1.1 机构降耦设计

1.1.1Quadrupteron并联机构

图1 Quadrupteron并联机构Fig.1 Kinematic diagram of Quadrupteron

Quadrupteron并联机构如图1所示[22]，由1条CRR支链(Leg 1)和3条CRRR支链(Leg 2、Leg 3、Leg 4)连接定平台和动平台；与动平台相连的4个R副的轴线与动平台的法线相互平行；每条支链上其余的C副和R副轴线互相平行。

易知，当定平台上4个C副的移动作为驱动时，动平台可实现三平移和绕动平台法线的转动输出；同时，该机构由1个基本运动链(BKC)组成，且耦合度κ=2，其运动学正解及动力学正反解求解复杂。

1.1.2降耦设计

文献[15]提出的基于运动副复合的结构降耦设计方法，已对多种耦合度较高的并联机构进行了拓扑降耦优化设计[15-18]。由于Quadrupteron机构动平台上的4个R副轴线平行，可以通过合并的方法达到机构结构降耦的目的。

保持CRR支链(Leg 1)不变，首先将图1所示Quadrupteron并联机构的2条CRRR支链(Leg 2和Leg 3)上与动平台连接的2个转动副重合，合并成RD副，移至动平台的中心；再拆开另1条CRRR支链(Leg 4)与动平台相连的R副，并通过末端执行件与RD副相连，则构成图2所示的新型降耦机构，记为(3CRR/R)&CRRR并联机构。

图2 (3CRR/R)&CRRR降耦并联机构Fig.2 (3CRR/R)&CRRR decoupled PM

这样，降耦机构由静平台0、中间平台1和末端执行件2组成。其中，静平台0和中间平台1之间由转动副R12、R13、R22、R23、R32、R33和圆柱副C11、C21、C31及相应构件组成，且满足C11‖R12‖R13、C21‖R22‖R23、C31‖R32‖R33，装配时C11、C21、C31互相正交；另一支链由C41、R42、R43和R44(正交的两转动副R43、R44可采用万向节代替，记为U43)组成；旋转轴RD固定在中间平台1上，且垂直于中间平台1；主动输入为C11、C21、C31、C41的移动。

1.2 拓扑结构特征分析

1.2.1机构的POC计算

并联机构的POC方程[22]为

(1)

(2)

式中MJi——第i个运动副的POC集

Mbi——第i条支链末端的POC集

MPa——机构动平台的POC集

m——运动副数

v——独立回路数

静平台0与中间平台1及3条Ci1Ri2Ri3(i=1,2,3)支链可看成一子并联机构。

确定中间平台1的POC集为

即子并联机构可看成是1条三平移输出的等效支链SOC{-P-P-P-}。

末端执行件的POC集为

因此，机构自由度为4，具有空间任意方向的移动和绕垂直于中间平台1法线方向的转动，与Quadrupteron机构输出特性相同。

1.2.2机构的自由度计算

并联机构DOF公式[22]为

(3)

(4)

v=m-n+1

式中F——机构自由度

fi——第i个运动副的自由度

n——构件数

ξLj——第j个独立回路的独立位移方程数

Mb(j+1)——前j+1条支链末端构件POC集

机构所含的独立回路数为

v=m-n+1=14-12+1=3

机构的拓扑结构路线可以分解为

SOC1{-C11‖R12‖R13-R23‖R22‖C21-}

SOC2{-C31‖R32‖R33-}

SOC3{-RD‖R44⊥R43‖R42‖C41-}

由式(4)得

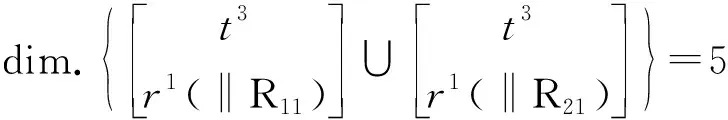
其构成子并联机构PM(1-2)的自由度和POC集为

由式(2)得

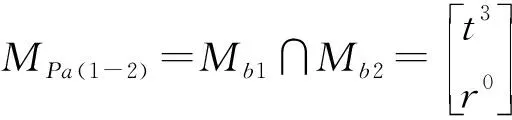
其子并联机构PM(1-3)的自由度和POC集为

由式(2)得

由式(3)得

因此，该降耦机构的自由度仍为4，当取静平台0上C副的移动作为驱动副时，末端输出件2可实现3个平移及1个转动的运动输出。

1.2.3机构耦合度κ计算

由基于序单开链(Single open chain, SOC)的机构组成原理[22]可知，任一机构可分解为约束度为正、零、负的3种有序单开链(SOC)，第j个SOCj的约束度定义为

(5)

式中mj——第j个SOCj的运动副数

Ij——第j个SOCj的驱动副数

进一步，一组有序的v个SOC可组成一个零自由度的独立回路数为v的基本运动链(Basic kinematics chain, BKC)，对一个BKC而言，须满足

(6)

因此，BKC的耦合度为

(7)

已计算出机构3个回路的独立位移方程数，分别为ξL1=5,ξL2=4,ξL3=5，因此，由式(5)可得：

SOC1的约束度为

SOC2的约束度为

SOC3的约束度为

则SOC3构成另一基本运动链BKC2，耦合度κ2=0。

1.2.4降耦机构运动解耦性分析

对图2所示的降耦机构进行解耦性分析如下：

(1)降耦机构可分解为2个BKC，如图3所示。其中，BKC1由SOC1和SOC2构成，即由静平台0、中间平台1及其间的3条Ci1Ri2Ri3(i=1,2,3)支链组成；另一个BKC2由C41、R42、U43、RD组成。

图3 降耦机构的拓扑结构组成Fig.3 Topological structure of decoupled PM

(2)由于机构的4个驱动位于不同的BKC，满足文献[22]的并联机构解耦性准则条件，则降耦机构具有部分自由度，即机构输出具有运动解耦。

(3)末端输出件2的位姿取决于所有主驱动输入，与其相邻的中间平台1(包括转动副RD)的位姿取决于部分输入；末端输出件2与中间平台1的平移运动重合，同时，末端件2绕转动副RD相对于中间平台1以角φ旋转。

用同样的方法，对Quadrupteron机构进行了上述的拓扑结构特征分析，分析结果如表1所示。

结果表明，降耦机构的自由度、POC集与Quadrupteron相同，均为3T1R；但运动副数和构件数均有所减小，故降耦机构的结构设计、制造更为简单；从拓扑结构组成来看，Quadrupteron由一个BKC组成，耦合度κ=2；而降耦机构由两个BKC组成，耦合度分别为1和0，且降耦机构的输出具有部分解耦性，表明降耦机构的运动学正解及动力学分析的难度将会大大降低。

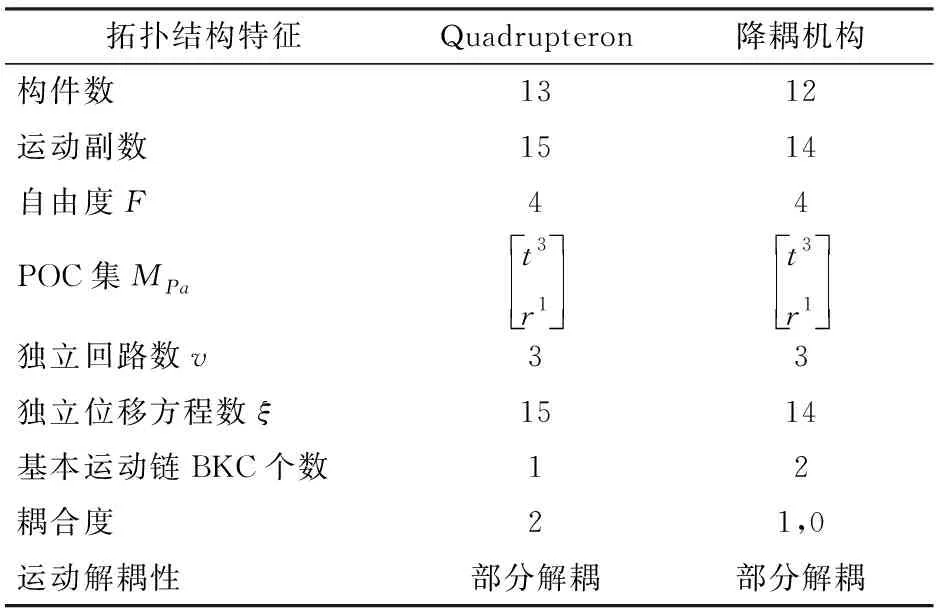
表1 两种并联机构的拓扑结构特征Tab.1 Topological structure characteristics of two PM

2 运动学分析

静平台采用框架形式，建立如图4所示定坐标系Oxyz，z轴与C11轴线平行，x轴平行于C31轴线；θi1(i=1,2,3)分别为构件A1B1与x轴、构件A2B2与x轴、构件A3B3与z轴的夹角；4个移动驱动滑块分别安装在间距为L的4个轨道上；驱动副行程为ρ，安装中心分别记为Gi(i=1,2,3,4)；每个分支的定长杆AiBi及BiCi长度设为lij(i=1,2,3;j=1,2)。

图4 并联机构运动示意图Fig.4 Kinematic diagram

在中间平台1的N点建立动坐标系Nuvw，v轴平行于转动副R23轴线方向，w轴平行于中间平台1的法线；点Ci(i=1,2,3)是转动副Ri3(i=1,2,3)在中间平台1上的安装基点，其特征参数是r，且有|NCi|=r(i=1,2,3)，并设Ci在Nuvw坐标系下的位置矢量为ri，βi(i=1,2,3)为NCi与u轴的夹角，如图5所示。

图5 中间平台1上运动副的分布Fig.5 Distribution of pairs on moving platform-1

图6 基本运动链BKC2示意图Fig.6 Sketch of BKC2

基本运动链BKC2的结构如图6所示，θ41为构件A4B4与x轴的夹角；定长杆A4B4及B4C4杆长分别为l41、l42；末端输出件C4D长度为l。

设驱动副的输入变量为ρ=(ρ1,ρ2,ρ3,ρ4)，末端输出件基点D位姿为x=(xD,yD,zD,φ)，则4条支链存在以下关系：

支链1

(8)

支链2

(9)

支链3

(10)

C4坐标满足如下关系

(11)

式中h——转动副安装基点D与点N距离，见图6

则由式(8)～(11)，可得

ρ2-rsinβ2=ρ4-lsinφ

(12)

2.1 机构位置正解

已知机构的输入位移(ρ1,ρ2,ρ3,ρ4)，求末端输出点D的位姿(xD,yD,zD,φ)，即为位置正解。

由式(8)～(12)，有

(13)

sinφ=(ρ4-ρ2+rsinβ2)/l

(14)

解式(14)，可得：

(1)当|ρ4-ρ2+rsinβ2|/l<1时，φ有两组解

φ1=arcsin(|ρ4-ρ2+rsinβ2|/l)

(15)

φ2=arcsin(|ρ4-ρ2+rsinβ2|/l)+π

(16)

(2)当|ρ4-ρ2+rsinβ2|/l=1时，φ有一组解。

(3)当|ρ4-ρ2+rsinβ2|/l>1时，φ无解。

分析表明，对于给定的、非奇异输入，末端执行件有两组姿态；而当初始装配情形确定后，机构的运动学正解具有唯一性。

2.2 机构位置反解

已知末端输出基点D的位姿(xD,yD,zD,φ),求机构的输入位移(ρ1,ρ2,ρ3,ρ4)，即为位置反解。

由式(13)、(14)可直接得出机构反解方程为

(17)

对式(13)、(14)整理，可得末端基点的输出矩阵形式为

(18)

式中 ·——输出常数

fi(·)——结构参数构成的函数

由式(18)可知，该机构的解耦性具有两层含义：①末端输出件的位置与姿态具有拓扑解耦特性。②末端输出的移动本身具有解耦特性，且具有各向同性，这为控制带来了方便。

3 机构雅可比矩阵及奇异性分析

3.1 机构雅可比矩阵

将式(17)对时间t求导，整理得

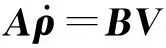
(19)

用矩阵A和B来分析机构奇异特性，并记J=A-1B为机构的雅可比矩阵。

3.2 奇异性分析

并联机构接近或到达奇异位形时，动平台将变得不可控。基于机构的雅可比矩阵，GOSSELIN等[23]将并联机构的奇异位形分为3类：正解奇异、反解奇异及混合奇异。发生正解奇异的条件是：|B|=0、|A|≠0，此时即使驱动副固定，机构末端仍能运动；当|A|=0、|B|≠0时，机构出现反解奇异，在发生反解奇异时，末端执行元件会失去一个或多个自由度；当正解奇异和反解奇异同时发生时，发生混合奇异。

对于(3CRR/R)&CRRR降耦并联机构来说，奇异分析包括两部分：①BKC1奇异，即静平台0、中间平台1及3条Ci1Ri2Ri3(i=1,2,3)支链组成子并联机构部分的奇异。②BKC1和BKC2组成的3回路(记为：BKC1+BKC2)机构的奇异。

3.2.1BKC1奇异分析

由式(19)前3项可知，三平移输出子并联机构的雅可比矩阵为正交单位矩阵，不存在正解奇异；对反解奇异，当每条Ci1Ri2Ri3(i=1,2,3)支链的3个运动副轴线共面时发生，属于工作空间的边界奇异。因此，解耦3CRR子并联机构在全工作空间内部不存在奇异位形。

3.2.2BKC1+BKC2奇异分析

(1)反解奇异

由式(19)可知，A是单常数阵，|A|恒不等于0，故不存在反解奇异。

(2)正解奇异

由|B|=0可得

cosφ=0

(20)

式(20)有两组解，即φ=π/2、φ=-π/2。这2个奇异姿态将降耦机构的工作空间分为2个无奇异工作空间区域：① 无奇异区域Ⅰ(-π/2<φ<π/2)，此时cosφ>0。② 无奇异区域Ⅱ (π/2<φ<3π/2)，此时cosφ<0。

只要机构远离这2个姿态(φ=π/2和φ=-π/2)，则机构不会发生反解奇异。

(3)混合奇异

由于|A|=0及|B|=0不可能同时成立，故机构不存在混合奇异位形。

3.2.3无奇异工作空间内运动学正解的分布

以上分析可知，机构无奇异工作空间包括：无奇异区域Ⅰ和无奇异区域Ⅱ；而运动学正解分析表明，机构存在两组运动学正解。根据式(15)、(16)、(20)可知，机构运动学正解的2个公式分别对应机构的无奇异工作空间区域Ⅰ和Ⅱ，如表2所示。

表2 机构无奇异工作空间区域内运动学正解Tab.2 Forward kinematics among singularity-free workspace

一旦机构装配形式给定，则确定了机构的无奇异工作区域，根据表2的计算公式可直接计算出机构的唯一运动学正解。

图4所示构型处于无奇异工作区域Ⅰ，则可采用式(13)、(15)进行运动学正解求解，这进一步简化了机构的运动学正解分析过程。

4 工作空间分析

对于3T1R并联机构，通常研究定姿态工作空间和可达工作空间。定姿态工作空间为机构动平台姿态保持一定时，动平台上参考点所能到达的区域；可达工作空间，是动平台上参考点以至少任一姿态能够到达的点的集合。

对大多数3T1R并联机构而言，动平台不同的姿态对应的工作空间大小不同，且相差较大。

由式(13)可知，本文提出的降耦并联机构，末端执行件3个方向的平移运动只与机构3个方向的驱动输入参数分别相关，与姿态角φ无关，故下文直接讨论机构的可达工作空间。

4.1 可达工作空间

由表3可知，工作空间随λ的增大先增加后保持不变，整个工作空间形状规则，且无内部空洞；当λ≤1时，工作空间是边长为ρ的立方体；当λ>1时，工作空间形状为一多面体；当λ>1.675时，工作空间形状和体积均保持不变。因此，为使机构结构紧凑、且获得规则形状的较大工作空间，驱动副行程不超过支链两定长杆长度之和。

表3驱动副行程对工作空间体积的影响
Tab.3Influenceofdrivingstrokeonworkspace

4.2 转动能力分析

由式(14)可知，末端机构的转动姿态仅仅决定于2个输入参数ρ2和ρ4，如保持ρ2、ρ4的驱动关系不变，可达工作空间内每一位置转动能力均相同；且每一位置的无奇异转动范围均为：φ∈(-π/2,π/2)或φ∈(π/2,3π/2)。

目前研究的文献中，除采用特殊的放大机构外，大多数3T1R并联机构的转动范围均在[-90°,90°]之内，且工作空间内点的转动能力差异较大。

5 算例

为便于性能比较，参照Quadrupteron样机结构参数，机构主要尺寸参数如表4所示[20]。增加的末端执行件C4D的长度为40 mm，移动副驱动行程为220 mm，机构三维虚拟装配如图7所示。

5.1 运动学正反解算例

由图7可知，该装配形式使得机构总工作在无奇异区域Ⅰ，给定两组主动输入参数：①ρ1=0，ρ2=0，ρ3=0，ρ4=0；②ρ1=10，ρ2=40，ρ3=30，ρ4=20。运用式(15)、(13)，求得对应的实数正解，如表5中序号①和②所示。

表4 机构的几何参数Tab.4 Geometric parameters of mechanism mm

图7 降耦并联机构的CAD模型Fig.7 CAD model of decoupled parallel mechanism

将表5中①、②正解数据，代入反解式(17)中，可得实数反解(序号③和④)。它与上述给定的输入参数一致，故认为正反解求解正确。

表5 (3CRR/R)&CRRR机构位姿正反解算例Tab.5 Positive and inverse solution example of(3CRR/R)&CRRR

5.2 工作空间及转动能力分析

由4.1节和4.2节分析可知，不考虑机构约束时，机构可达工作空间是一规则立方体，边长为驱动副行程，即机构工作空间是边长为220 mm的立方体，且工作空间内每一位置的转动能力均一致，为(-90°,90°)，且无内部奇异。

由于各被动关节转角限制以及杆件可能发生干涉，实际工作空间小很多。本文基于位置反解式(17)，采用搜索法求解出满足约束条件的所有点，再利用所有满足约束条件的“点集”近似求解出工作空间体积。求解步骤如下：

(1)根据经验初步估算出工作空间的搜索范围为：35 mm≤XD≤315 mm，31 mm≤YD≤365 mm，0≤ZD≤270 mm。

(2)基于位置反解式(17)求解并联机构的输入参数(ρ1,ρ2,ρ3,ρ4)，同时满足如下约束条件：①支链各被动关节的转角必须限制一定范围：-75°≤θi1≤75°，15°≤θi2≤165° (i=1,2,3)。②驱动副行程为220 mm。③根据奇异条件，末端输出件2的转动姿态必须满足(-90°,90°)。

(3)给定末端输出件姿态角φ，并将步骤(1)中的初始化输出参数代入反解式(17)中。

(4)选取搜索步长因子Δx=Δy=Δz=10 mm，若通过步骤(1)～(3)计算的结果满足所有约束条件，则为工作空间内有效点，否则返回步骤(1)，并按步长依次改变末端件的输出位置参数。

根据表4给定的机构参数，在Matlab中编程计算，求解给定姿态φ下的“点数”nφ，而每个点可视为边长为Δx的小正方体。因此，可求得定姿态下工作空间体积为(单位：mm3)

Vφ=nφ(Δx)3=103nφ

(21)

采用同样的步骤，对Quadrupteron机构的定姿态工作空间体积进行计算。图8是不考虑转动关节角度限制时，(3CRR/R)&CRRR降耦机构和Quadrupteron[20]的Vφ与φ的关系曲线。

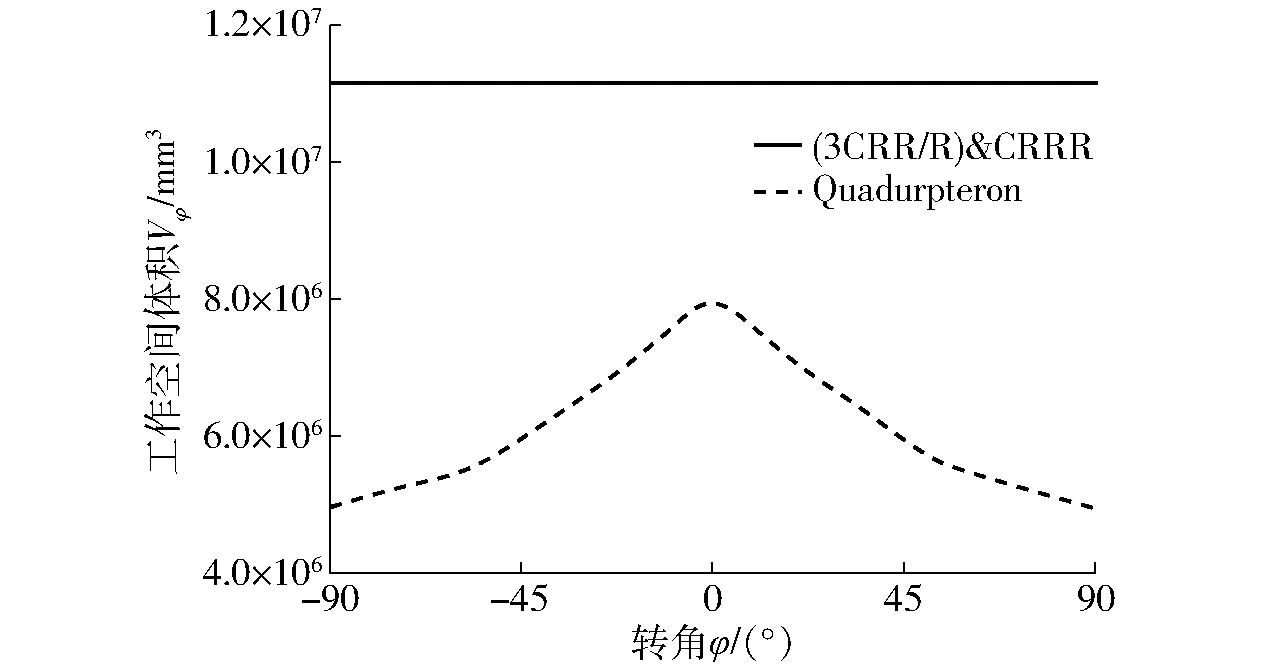
图8 定姿态工作空间体积随φ的变化(不考虑约束)Fig.8 Changes of Vφ with φ (without constraints)

由图8可知：①对(3CRR/R)&CRRR降耦机构，全工作空间转动能力保持不变，即工作空间内所有位置点的转动能力一致，工作空间体积达1.11×107mm3。②对于Quadrupteron机构，在姿态角为0°时，定姿态工作空间体积达最大，Vφmax=8.33×106mm3；当姿态角接近±90°时，定姿态工作空间体积最小，Vφmin=4.95×106mm3；其最小、最大工作空间体积降幅达40%以上，与文献[21]的结论一致。因此，降耦机构的定姿态工作空间体积及转动能力较Quadrupteron并联机构都有显著提升。

5.3 降耦机构的实际定姿态工作空间

图9是考虑转动副角度范围限制时，降耦机构(3CRR/R)&CRRR定姿态工作空间体积随末端输出姿态φ的变化情况。由图9可知：①考虑运动副转角范围限制后，降耦机构实际定姿态工作空间体积有所减小，可见，合理设计被动关节的安装角，可提高并联机构的工作空间。②降耦机构在初始姿态，即φ=0时，定姿态工作空间体积达最大，约为9.398×106mm3；随着姿态角的增加，定姿态工作空间体积减小；当转角接近±90°时，定姿态工作空间体积最小，为6.519×106mm3。故在考虑转动约束的情况下，降耦机构定姿态工作空间体积的最大降幅达30%，小于Quadrupteron在理想状态下最小、最大工作空间的降幅(大于40%)。这进一步表明，考虑转动副角度范围限制时，降耦机构的实际定姿态工作空间比Quadrupteron机构有较大改善。

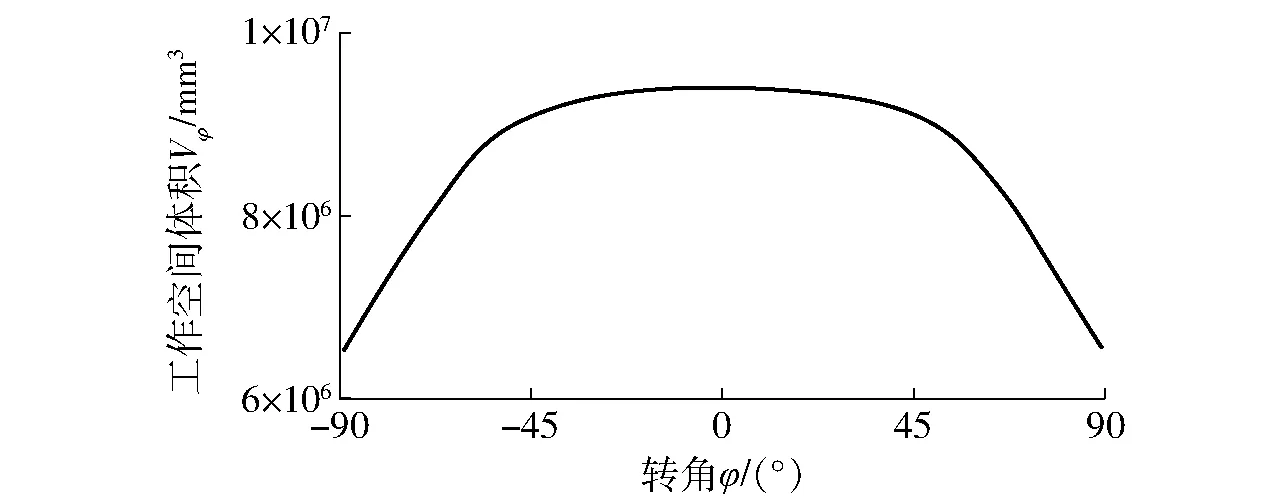
图9 (3CRR/R)&CRRR机构的Vφ与φ关系曲线(考虑约束)Fig.9 Relationship curve between Vφ with φ(with constraints)

6 结论

(1)通过运动副复合的方法，对Quadrupteron并联机构进行降耦设计，提出了一种耦合度较低的3T1R新机型。

(2)该降耦机构具有输出运动解耦特性，机构3个方向的移动输出与3个输入参数一一对应，而转动姿态与其中2个输入参数相关。

(3)机构结构简单、运动学正反解方程更简单，方便制造、控制。

(4)在(-90°,90°)输出转角范围内，机构无内部奇异存在；且机构具有较大体积的规则工作空间，全工作空间内所有位置的转动能力一致。

(5)该降耦机构克服了一般并联机构耦合性强、控制复杂的弱点，转动能力大幅度提高，具有较好的工业应用前景。