基于改进粒子群算法的路径规划

贾会群 魏仲慧 何 昕 张 磊 何家维 穆治亚

(1.中国科学院长春光学精密机械与物理研究所， 长春 130033； 2.中国科学院大学， 北京 100049)

0 引言

路径规划是机器人研究中最基本、最关键的问题[1-4]，目的在于寻找到一条从起点到终点的最短路径，使机器人安全到达预定的目的地。近些年，专家学者们提出很多有关机器人路径规划的算法[5-15]。一类是传统方法，如视图法[8]、人工势场法[9]、自由空间法[10-11]等；另一类是新兴的智能仿生算法，如粒子群算法[7]、鸡群算法[12]、蜂群算法[13]、狼群算法[14]、鸟群算法[15]等。相较于传统的算法，通过模拟生物的一种或几种行为而提出的智能仿生算法，为解决复杂环境下的路径规划问题提供了新思路。

粒子群算法(Particle swarm optimization, PSO)是一种模拟鱼群的仿生算法，具有易于实现、收敛速度快、所需调整的参数少等优点，一经提出便得到学术界的广泛关注[16-20]。针对PSO的研究主要集中在参数调整[16-18]、种群结构改进以及与其他方法相结合的改进[19-20]。文献[16]通过分析惯性权重因子ω大小同PSO收敛性的关系，提出了线性自适应惯性权重因子的PSO改进算法，提高了算法的收敛性。文献[17]在迭代过程中将适应度值较差的粒子的惯性权重因子置零，减小了算法的无效迭代，使算法的收敛性得到进一步提升。文献[18]通过分析加速因子c1、c2和PSO收敛性的关系，提出了线性的自适应加速因子的PSO改进算法，使算法的收敛性获得了一定的改善。文献[19]提出了PSO和遗传算法的混合算法用于路径规划，文献[20]提出了雁群和PSO混合算法进行路径规划。虽然已有文献对PSO进行了研究和改进，但目前粒子群算法依然存在收敛精度低、搜索停滞等缺点，导致在路径规划时不能得到最优的规划路径。

针对目前算法存在的问题，受文献[12，18]的启发，通过分析文献中方法的优缺点，本文提出使用三角函数的变化方式自适应地调整惯性权重因子和加速因子，使惯性权重因子和加速因子在算法运行各阶段的配合最佳，提高算法的搜索能力；然后引入母鸡和小鸡两种更新方程对搜索停滞的粒子进行扰动，提高粒子群的多样性，并在引入的方程中使用粒子群全局最优解，使得扰动后的粒子向全局最优解靠近，减少无效扰动，以提高算法的收敛精度及稳定性。

1 PSO算法的数学理论

文献[21]首次提出粒子群算法，假设粒子群规模大小为n，搜索区域维数为D，xi=(xi1,xi2,…,xiD)为粒子i(i∈1,2,…,n)在搜索区域的位置，vi=(vi1,vi2,…,viD)为粒子i的速度，pi=(pi1,pi2,…,piD)为粒子i搜索的最优位置，pg=(pg1,pg2,…,pgD)为粒子群搜索的最优位置，则对于第k+1次迭代，粒子的位置更新公式为

(1)

(2)

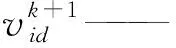
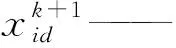
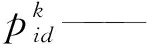
ω——惯性权重因子

c1、c2——加速因子

rand()——(0,1)间的随机数

2 PSO算法的改进

造成传统的PSO收敛精度低，搜索停滞的原因有[22]：① 算法收敛后期，因粒子群多样性降低，导致算法陷入局部最优值即“早熟”。② 因粒子容易被困在较差的搜索区域并很难跳出，造成搜索停滞，导致收敛效率低。为了解决上述问题，从粒子群参数及算法更新方程两方面进行改进。

2.1 PSO算法的参数改进

传统的粒子群算法的更新公式包括3部分：上一代粒子速度值、单个粒子学习部分和粒子群之间相互学习部分。第1部分受权重因子ω的控制，第2、3部分受加速因子c1、c2的控制。目前较多的研究主要集中在对一种参数的改进[16-17]，文献[18]对惯性权重因子和加速因子同时进行改进，相较于对一种参数的改进，两种参数同时改进的PSO算法在优化精度和收敛速度上具有一定的优势。但文献[18]中加速因子是在基于线性变化的基础上进行扰动，导致扰动效果并不明显。因此本文在文献[18]的基础上做进一步改进，即将线性变化的加速因子替换为非线性变化的加速因子，非线性扰动强度大，有利于提高种群的多样性，这对解决“早熟”问题是有利的。

本文惯性权重因子仍然使用文献[18]提出的余弦变化权重因子，其数学表达式为

(3)

其中ωmax=0.95ωmin=0.4

式中kmax——最终迭代次数

k——本次算法迭代次数

ω(k)——第k次迭代对应的惯性权重因子

根据式(3)画出不同迭代次数时惯性权重因子的变化曲线，如图1所示。

图1 ω变化曲线Fig.1 Variation curves of ω

根据式(1)，算法的学习部分受加速因子c1、c2的控制，c1控制单个粒子的学习部分，c2控制粒子群之间的相互学习部分。文献[20]中提到适当的调节加速因子可以优化算法的寻优过程，优化前期PSO算法进行全局搜索时要求个体从全局学习，因此要求前期c1取较大的值，后期PSO算法进入局部搜索时群体学习很重要，要求c2取较大的结果。经过分析，本文采用正弦函数模拟加速因子的变化，提出新的自适应加速因子

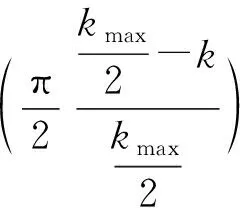
(4)

(5)

式中ca、cb、cα、cβ——待确定参数

按照文献[20]，c1在[0.5,2.5]和c2在[0.5,2.5]取值时，可得到较高的寻优结果，因此确定ca=1，cb=1.5，cα=1，cβ=1.5。图2、3分别为加速因子c1、c2随迭代次数的变化曲线。

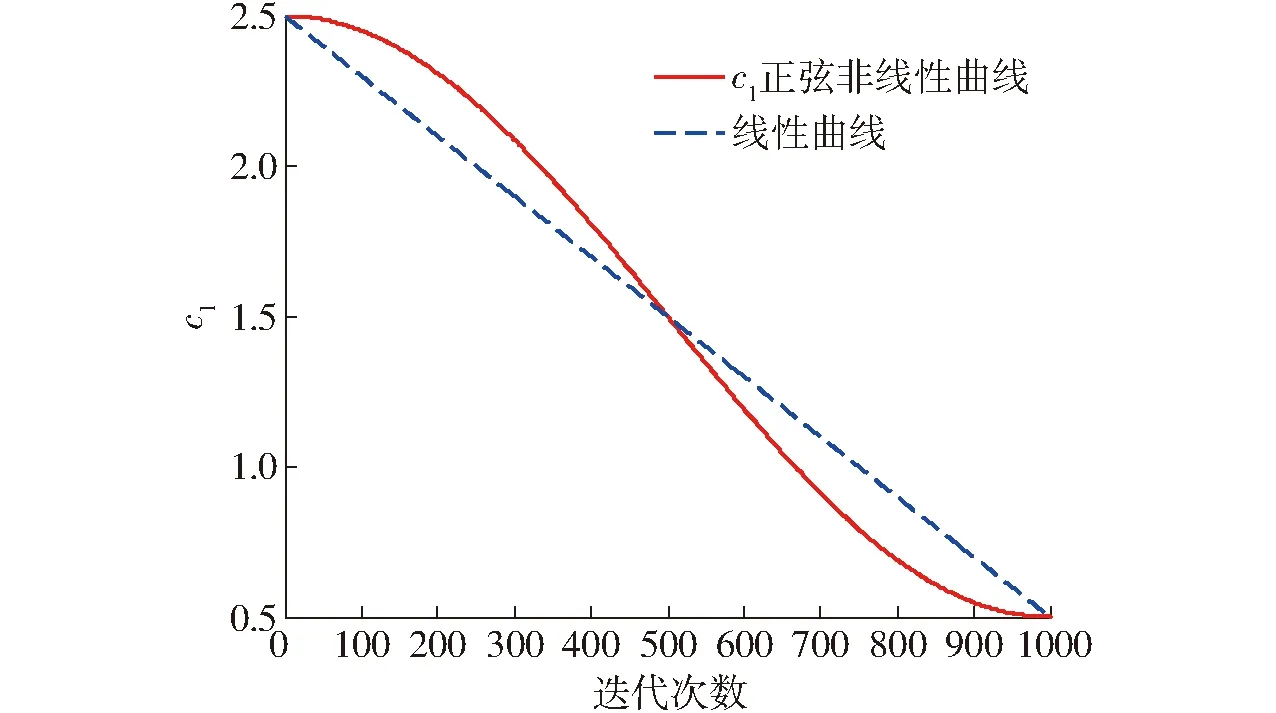
图2 c1变化曲线Fig.2 Variation curves of c1

图3 c2变化曲线Fig.3 Variation curves of c2

图1～3中实线为按三角函数规律变化的自适应惯性权重因子ω及加速因子c1、c2，虚线为各参数的线性规律变化。从图中可以看出，3个按照三角函数规律变化的参数之间是一种配合的关系，这是因为算法迭代前期惯性权重因子取值较大，PSO算法进行全局搜索，此时加速因子c1大、c2小，有助于个体对全局的学习；到了后期惯性权重因子取值较小，PSO算法进行局部搜索，此时c1小、c2大，有助于局部搜索时群体的学习，并且3种参数都是按三角函数规律增大或减小，使得各参数的大小配合达到最佳，提高算法的搜索能力。

将所提的按三角函数规律变化的惯性权重因子和加速因子方程代入式(1)、(2)得

(6)

(7)

式(6)、(7)为含有自适应参数的PSO算法的位置更新公式。

2.2 引入多种更新策略

当粒子被困在较差的搜索区域时，算法的优化结果一般会变差[17]，本文的优化问题是求取最小值，其变差的情况表示为

f(xk+1)>f(xk)

(8)

式中f(xk+1)——第k+1次迭代所得适应度值

f(xk)——第k次迭代所得适应度值

如果算法运行时连续3次迭代出现式(8)描述的情况，认为粒子处于较差的搜索区域，粒子出现无效搜索。为了解决这一问题，本文受鸡群算法[12]的启发，通过引入鸡群算法中母鸡和小鸡2种不同扰动强度的更新方程，对无效搜索的粒子进行扰动，其目的就是通过不同强度的扰动增加粒子的多样性，使粒子跳出较差的搜索区域，脱离局部最优。

当第1次判定粒子出现无效搜索时使用母鸡更新方程进行扰动

(9)

其中s1=exp((fi-fg)/(abs(fi)+ε))

(10)

s2=exp(fi-ft)

(11)

式中t——粒子序号，t≠i

fi——第i个粒子的适应度值

fg——全局最优适应度值

ε——保证分母不为零的极小数，本文调用Matlab 2014自带的极小数为2.225 1×10-308

s1、s2——学习因子

abs()——取绝对值函数

当式(9)扰动失败即粒子使用式(9)更新之后仍然是无效搜索状态，这时将加大扰动强度使用小鸡更新方程进行扰动。

(12)

式中FL——[1,2]之间的任意实数，为了获得较大的扰动，本文取FL=2

式(12)类似于鸟群算法中鸟群飞行行为[15]，可以使粒子从一个位置跳到另一个位置。

式(9)、(12)为在原来方程的基础上改进后的方程，与原方程的不同之处在于改进后的方程都用了全局最优位置解，目的是在对这些搜索较差的粒子进行扰动时，同时使这些粒子向全局最优位置靠近，避免了无效扰动，有利于提高算法的搜索效率。

改进后算法流程如下：

(1)PSO算法各参数初始化包括粒子初始位置、初始速度等，令迭代次数k=1。

(2)计算粒子的适应度值，计算当前各粒子的个体最优值以及种群的全局最优值。

(3)使用式(6)、(7)对粒子更新。

(4)连续迭代3次，判断f(xk+1)>f(xk)是否成立，成立转至步骤(5)，否则转至步骤(8)。

(5)使用式(9)对粒子进行扰动。

(6)连续迭代3次，判断f(xk+1)>f(xk)是否成立，成立即式(9)扰动失败转至步骤(7)，否则转至步骤(8)。

(7)使用式(12)对粒子进行扰动。

(8)计算位置更新后各粒子的适应度值并更新个体最优适应度值以及全局最优适应度值。

(9)判定k是否达到最大迭代次数，若是输出最优收敛结果，否则转至步骤(3)。

3 实验结果与分析

为了验证本文对传统粒子群算法改进的有效性，本文任意选取5个标准测试函数进行函数优化，并将其应用于机器人路径规划，从实际应用来验证算法的有效性，实验平台为Matlab 2014。

3.1 函数优化

选取的5个测试函数包含了多种类型，其基本的数学性质如表1所示，表中U表示单峰值，M表示多峰值，N表示不可分离，S表示可分离。

表1 标准测试函数Tab.1 Standard test function

为了保证实验所得数据的有效性，每个标准测试函数单独进行50次统计实验，根据统计结果计算出最优值、平均最优值(Mean)和标准差(Std)，对改进算法(WCPSO)的性能进行评价。对比算法选用传统算法即固定惯性权重粒子群算法[21](PSO)、线性自适应惯性权重因子粒子群算法[16](WPSO)和线性自适应加速因子粒子群算法[18](CPSO)3种较为常用的算法。所有算法设置相同的参数：种群数60，迭代次数1 000。实验结果如表2所示。

从表2的整体优化结果可以看出，对于不同类型的函数，本文所提出的改进算法(WCPSO)均取得了较高的收敛精度并且优于其他算法，其次是WPSO，传统的PSO算法收敛效果最差。表2中，函数f3、f4、f5通过改变维度，验证各算法对不同维度函数的优化性能：对于f3，WCPSO在不同维度上均取得了优于其他算法的结果；对于f4、f5，在不同维度时所有算法均取得相似的最优结果，但从均值和方差可以看出，WCPSO稳定性明显优于其他算法。

3.2 路径规划实验

将改进的算法(WCPSO)应用到机器人路径规划，验证改进算法在实际应用中的有效性。

3.2.1环境模型

采用导航点模型[1]构建环境模型如图4所示，起点坐标(0,0)，终点坐标(9,8)， 障碍物数学表达式为

(x-a)2+(y-b)2=R2

(13)

式中 (a,b)——障碍物圆心坐标

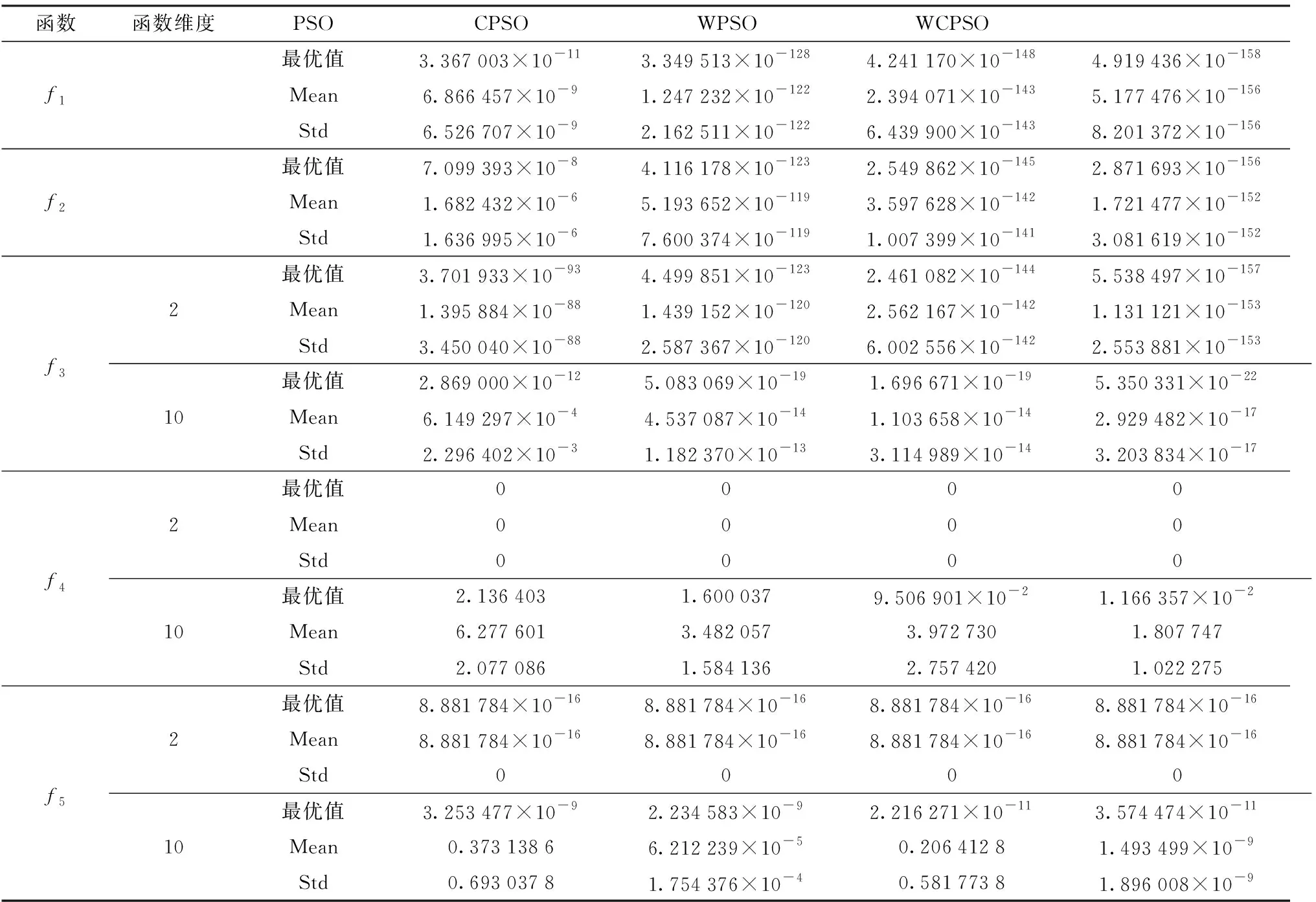
表2 函数优化结果Tab.2 Results of function optimization

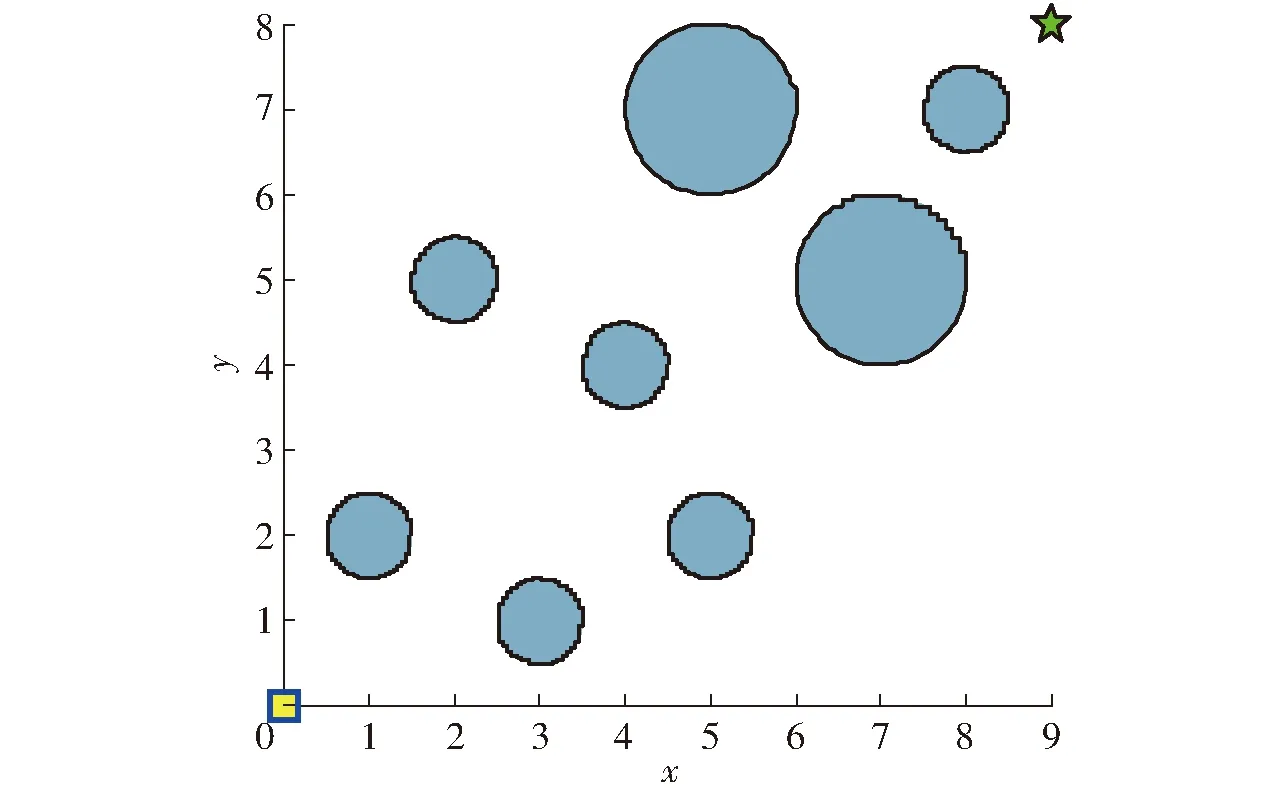
图4 环境模型Fig.4 Environment model

R——障碍物半径(图4中较大圆的半径为1，其余小圆的半径都为0.5)

3.2.2适应度函数

设起点坐标S(x0,y0)，终点坐标T(xn+1,yn+1)，一个粒子代表一条路径，其在x方向和y方向上的位置为X=(x1,x2,…,xn)，Y=(y1,y2,…,yn)。路径长度函数即适应度函数为

(14)

(15)

式中K——障碍物个数

V(k)——避障约束惩罚函数

w——安全因子，根据文献[1]设置w=100

R(k)——障碍物k的半径

图4中从起点到终点理论上最短的无障碍路径长度Lmin=12.141 590。

3.2.3实验结果分析

实验选用函数优化结果仅次于改进算法的WPSO算法作为对比算法，2种算法参数设置相同：种群规模150，迭代次数500。为了保证结果的可靠性，改进算法和对比算法分别进行10次独立实验。

图5为10次实验中WCPSO算法和WPSO算法所得到的路径长度曲线，绿色曲线是理论上最短的无障碍路径长度曲线。从图5中可以看出：10次实验中本文的改进算法更加接近理论值，并且一直保持较优的规划路径，算法稳定性较好；WPSO算法虽然也能获得较优的路径，但算法波动大，稳定性较差。图6、7分别为10次实验中WCPSO算法和WPSO算法路径规划的仿真结果。通过图6和图7的对比可以很直观地看出本文改进算法鲁棒性好、路径规划精度高的特性。

图5 实验对比结果Fig.5 Comparison of experimental results

4 结束语

为了解决目前粒子群算法中因存在搜索精度低、搜索停滞等现象，导致在机器人路径规划中不易获得最优路径的问题，本文对传统的粒子群算法进行改进，使用三角函数变化规律自适应地调整算法中的各个参数。与传统的线性自适应参数相比，基于三角函数规律变化的参数能够更准确地模拟在算法迭代过程中各个参数的变化趋势，使得各参数的大小配合达到最佳，从而使得各参数的作用充分发挥。通过在引入的母鸡和小鸡更新方程中使用全局最优解，对搜索停滞的粒子进行扰动，增加了粒子多样性，避免了搜索停滞的问题，实验结果表明改进的算法具有一定的应用价值。

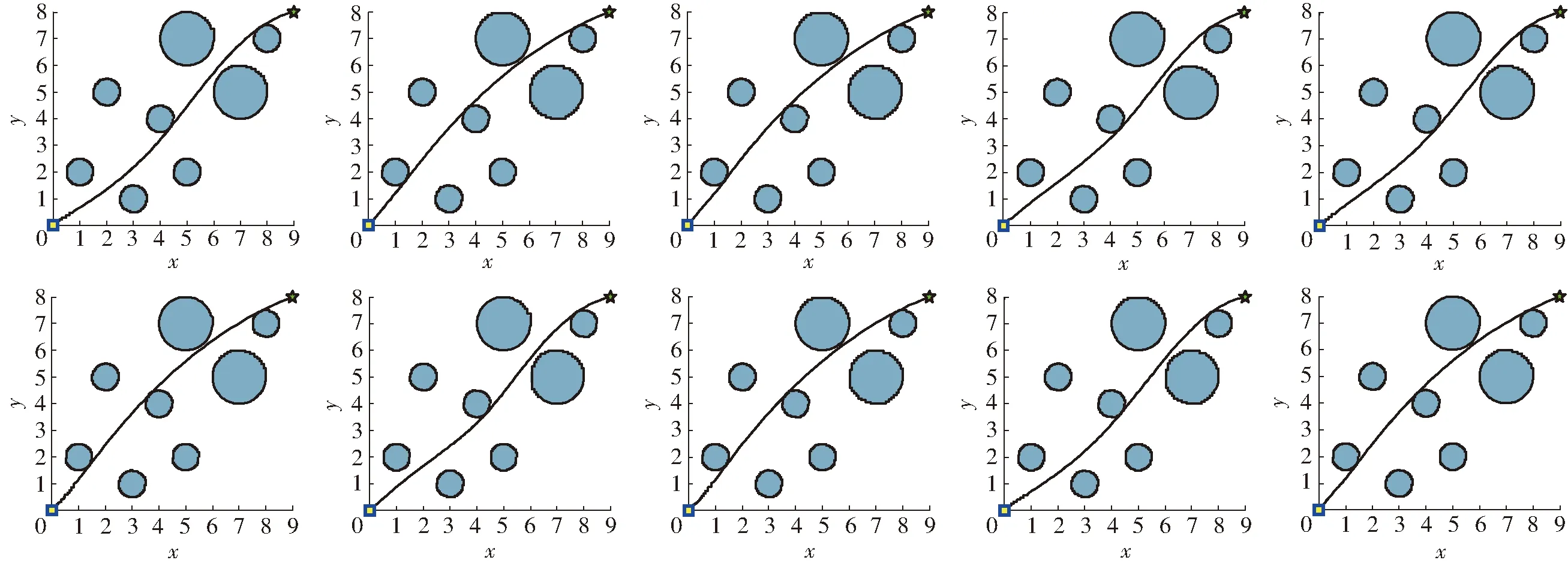
图6 改进算法路径规划结果Fig.6 Path planning results of improved algorithm