低比转数离心泵叶轮内流场重构与模态分析

张人会 陈学炳 郭广强 李仁年

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.甘肃省流体机械及系统重点实验室， 兰州 730050)

0 引言

离心泵水力性能的优化实质是对其内流动的优化控制，由于离心泵内部流动的复杂性及内部流动与其水力性能之间的复杂隐式关系，离心泵水力性能的优化设计研究进展缓慢[1-5]。目前叶轮机械优化设计方法主要有响应面法、遗传算法、伴随方法、不完全敏感性法等[6-9]。响应面法与遗传算法属于非梯度方法，全局最优，但随设计参数的增多，计算量剧增；伴随方法求解精度高、计算量小，但是伴随方程的推导及求解较为复杂。采用代理模型能够快速确定设计参数对流场的扰动响应，精确地进行流场的预估，有效避免大规模的流场计算，便于实现流场的快速优化。

本征正交分解(Proper orthogonal decomposition, POD)法是一种功能强大的数据分析方法[10]，其通过对数据系统的奇异值分解确定系统的POD基，在给定系统空间内具有最佳的表达能力。段焰辉等[11]在无粘跨音速情况下，使用本征正交分解法对机翼翼型流场进行了分析。文献[12-15]在Gappy POD翼型反设计方法的基础上提出校正迭代法，以此提高反设计精度，并将其与代理模型应用于流场的预测，得出基模态数与预测精度的关系。罗佳奇等[16]基于POD方法对跨音速叶片的流场进行分析，提出POD-RBF(本征正交分解-径向基函数)混合代理模型，并成功应用于跨音速流场的分析。文献[17-18]将本征正交分解法应用于离心泵的反设计研究，同时将其应用于液环泵单流道流场重构研究。

本文提出基于POD-RBF混合代理模型方法的离心泵叶轮内流场重构研究，并对离心泵叶轮内流场结构及模态特征进行流场基模态分析。

1 POD内流场重构及模态分析理论

1.1 Gappy POD本征正交分解法

SIROVICH[19]最早提出了Snapshot POD方法，该方法将自相关矩阵的阶数降低至与快照个数相等，大大改善了求解特征值的效率和稳定性问题，为POD方法在流体力学中的应用提供了便利。Gappy POD 是Snapshot POD方法的一种变形，常被用于缺失数据的填补。

样本快照集表示为

U=[U1u2]T

(1)

在矢量集U1中，所有元素都是已知的，矢量u2的表达式为

u2=[u21u22]

(2)

u21为已知数据，u22为缺失数据，需要完成对缺失元素的填补。

矢量集U1可表示为

(3)

其中

Φ=[Φ1Φ2]

(4)

式中Φ——POD基n——样本数

aj——基系数

其可通过快照集U的奇异值分解计算得到

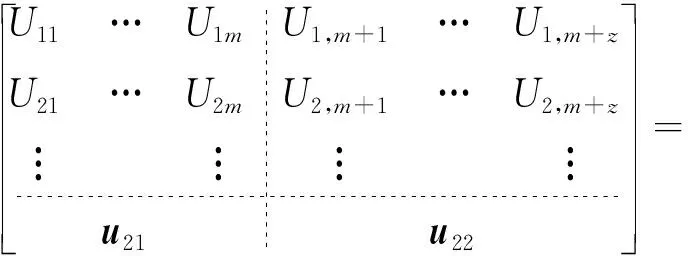
(5)

式中，Φ1、Φ2是对应于u21、u22两部分的POD基，bij与βj为POD基系数，下角标m为叶型参数的个数，下角标z为重构截面网格节点个数。对矢量u22可进行填补，即

(6)

系数βj可通过最小二乘法得到，即

Mβ=f

(7)

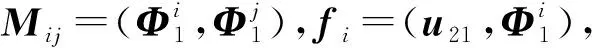
1.2 POD-RBF混合代理模型

在早期的Gappy POD的应用中，经常采用最小二乘法来确定POD基系数，这是一种线性回归方法，在非线性系统响应问题中精度较低。为了提高POD基系数的响应精度，采用非线性且响应精度高的径向基函数(Radial basis function, RBF)[20]来预测目标样本的正交基系数。

由样本快照集的奇异值分解可得

U=QΣVT=QΦ

(8)

式中Q——各样本对应的基系数

Σ——对角矩阵

V——右奇异矩阵

不同的样本叶型参数分别对应不同的正交基系数，可建立样本矢量与其基系数的径向基神经网络模型(Radial basis function neural network, RBFNN)

(9)

其中qkj为第k个POD基系数向量的第j个分量，Wij为RBFNN模型系数，xi为各样本叶型控制参数。φ(xi,xj)为径向基函数，采用高斯型径向基函数，其表达式为

φ(xi,xj)=e-σ‖xi-xj‖2

(10)

式中σ为正实数，0≤σ≤1。

由式(8)可得样本集的正交基矢量，由径向基网络的输入参数xi及其输出qkj可反解其RBFNN模型系数Wij，然后依据该RBFNN模型可预测目标叶型xo所对应的POD基系数qo，并由式(8)重构目标叶型所对应的叶轮内流场。

1.3 叶轮内流场的基模态分析

采用POD方法进行样本流场模态的提取，每个快照均由叶轮中间截面网格节点坐标和相应的流场信息构成，第i个样本矢量可表示为(xi,1,xi,2,…,xi,M×N|yi,1,yi,2,…,yi,M×N|vi,1,vi,2,…,vi,M×N)。其中(x，y)为网格节点坐标，v为流场参数，M×N为网格节点数。

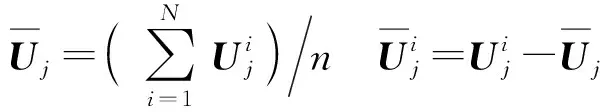
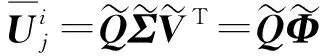
(11)

2 离心泵叶轮内流场重构及其模态分析

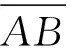
图1 叶片型线参数化控制Fig.1 Parametric control of blade shape

2.1 内流场重构及其误差分析

依据初始叶片型线基础上扰动所得各样本叶轮内流场的CFD计算结果，对初始叶型的叶轮内流场进行POD重构分析，并将流场的POD重构结果与其CFD结果进行误差分析。样本矢量由叶片型线的控制参数和叶轮内流场参数构成，第i个样本矢量可以表示为(αi,1,αi,2,…,αi,m|vi,1,vi,2,…,vi,53×41)，其中α是叶型参数，单个流道取53×41的网格节点数，由此可得样本集为

(12)

其中vo,i是目标叶型αo,i所对应的流场参数。

8个叶轮叶片型线各不相同，无法实现同一网格下的流场重构，由于各叶轮内流道几何相似，进行流场的重构时需要根据对应的相似节点进行流场样本集的构建，并进行流场预测。采用网格变形技术重构其结构化网格，将其单个流道网格统一为53×41的结构化网格，按照相似的网格节点进行流场的插值，得到各相似坐标点的样本矢量集。

定义沿着圆周角γ及半径r方向的无量纲坐标δi,j和ηi,j，其中δi,j满足公式

γi,j=γi,1+δi,j(γi,41-γi,1)

(13)

式中，γi,j为节点(i，j)所对应的圆周角坐标，类似地可定义r方向的无量纲坐标ηi,j。由均匀分布的无量纲坐标及叶片边界上的节点分布即可求解叶轮内任意相似节点的坐标。

通过POD-RBF混合代理模型对目标叶型对应的内流场进行重构，并将预测流场与CFD计算结果进行对比，如图2～6所示。

图2 CFD计算全流道压力分布Fig.2 Pressure distributions of whole channel of CFD

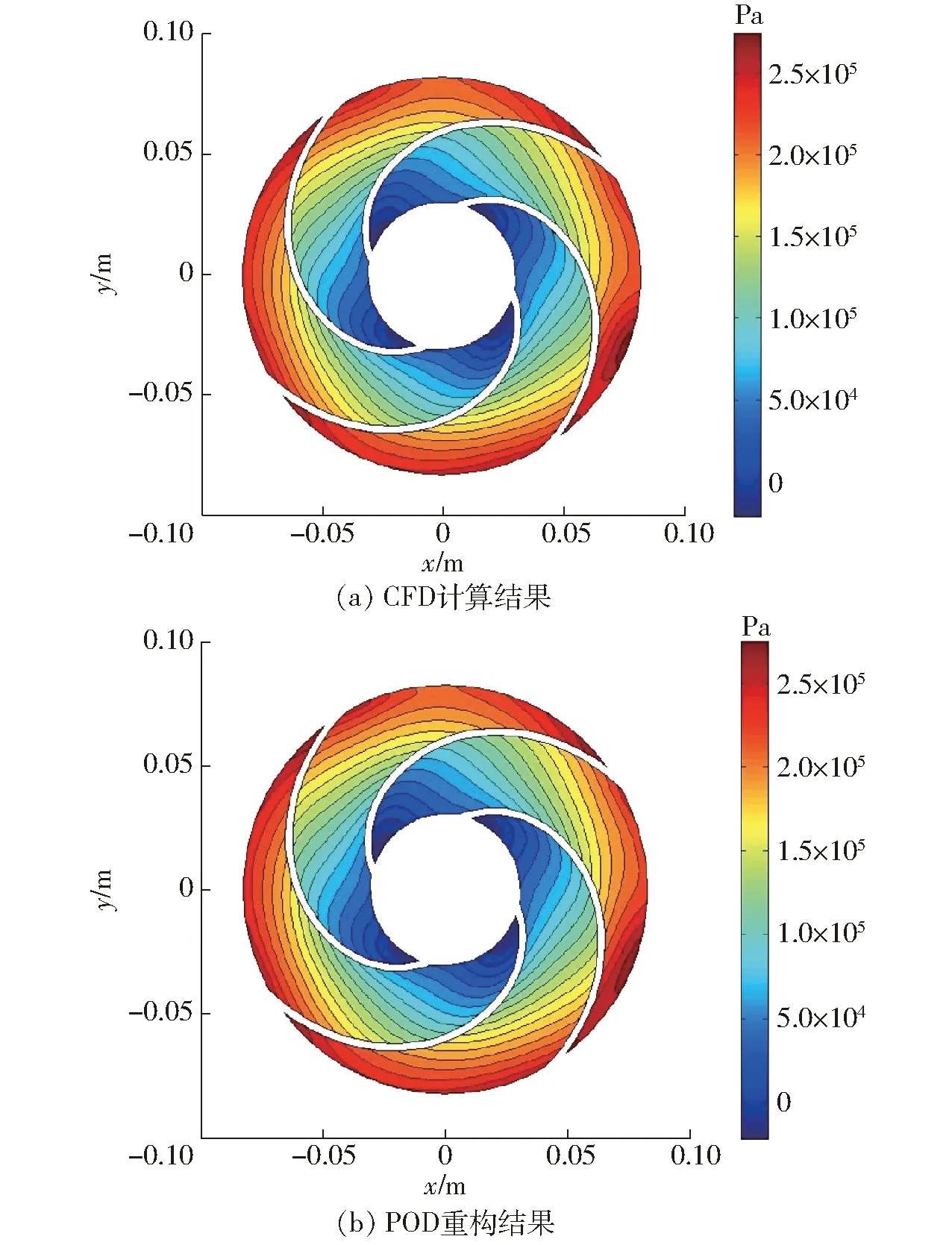
图3 CFD与POD重构的压力分布Fig.3 Pressure distributions of CFD and POD

(14)

其中fi,POD、fi,CFD分别为各网格节点的POD及CFD流场参数，K为叶轮中间截面网格节点总数。

图4 压力误差分布Fig.4 Distributions of pressure errors

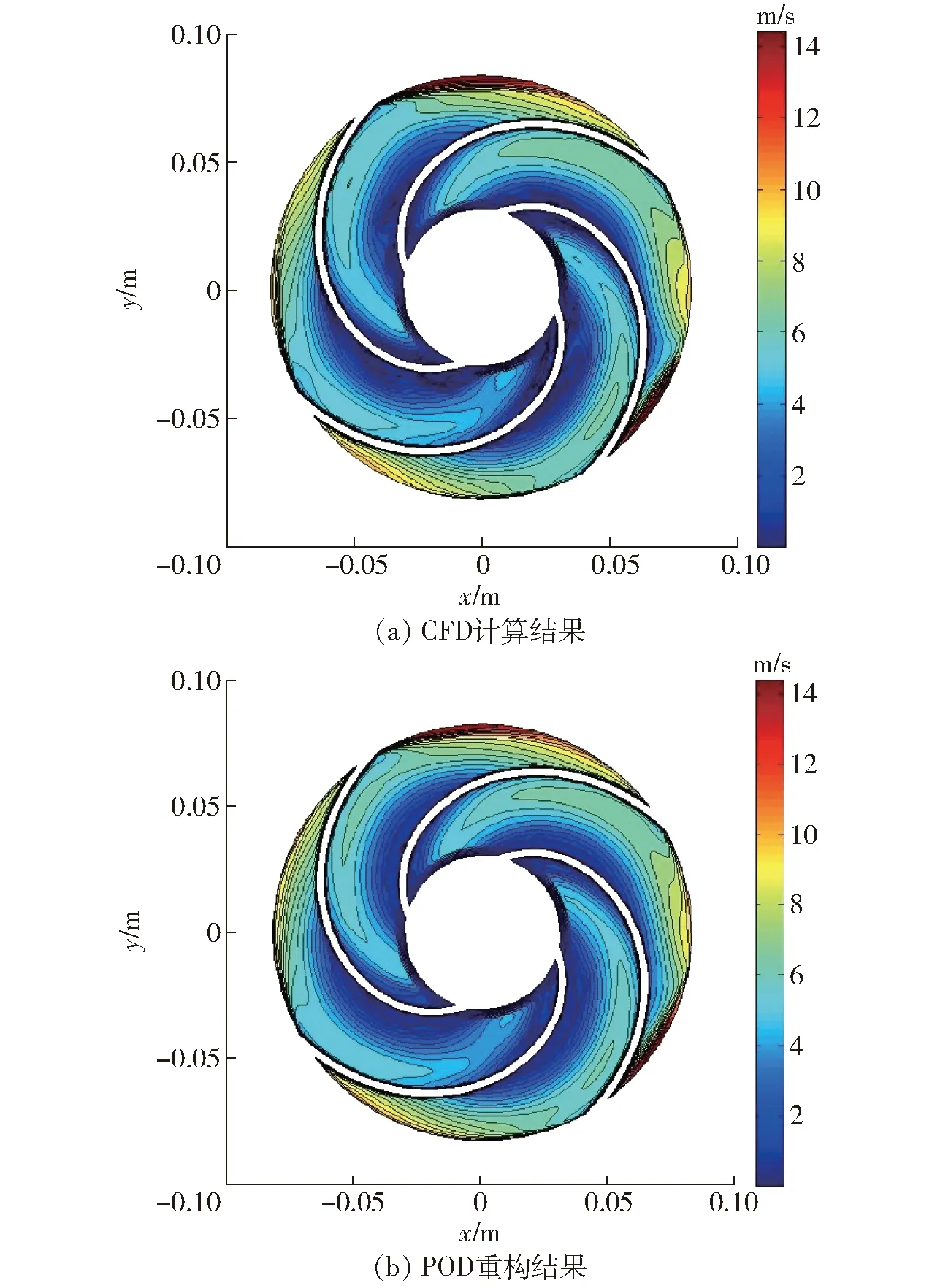
图5 CFD与POD重构的速度分布Fig.5 Velocity distributions of CFD and POD

图2是CFD计算全流道中间截面压力分布情况，可以看出由于隔舌动静干涉的影响，隔舌附近叶轮内压力较高。图3是叶轮中间截面压力场的POD预测结果与CFD计算情况的对比，由图可以看出POD预测结果与CFD计算基本一致，从叶轮进口到叶轮出口压力逐渐增大。图4是压力预测误差分布情况，是由POD预测压力场减去CFD计算流场得到。从图中可以看出，叶轮靠近蜗壳隔舌部位有较高的局部误差，约10 000 Pa，整体来看叶轮内流场压力预测误差基本在1 000～3 000 Pa，误差较小。根据式(14)计算可得均方根误差为0.84%。

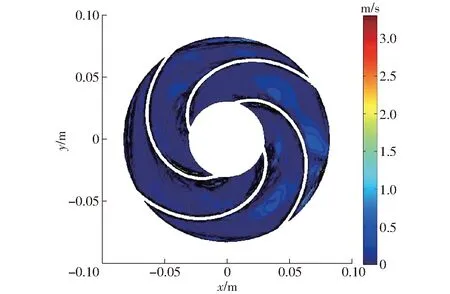
图6 速度误差分布Fig.6 Distributions of velocity errors

图5为叶轮中间截面相对速度的POD预测与CFD计算结果的对比，由图可以看出，POD-RBF混合代理模型法可以精确预测目标叶轮相对速度场的分布情况。图6为预测速度场与CFD计算速度场间的对比误差分布，可以看出预测误差基本在0.5 m/s以内。同样在DELL T620、24核、64 GB内存的工作站上进行运算， CFD计算泵内流场需要2 h才能完成，而由POD-RBF方法重构叶轮内流场所需要的预测时间大约为30 s，仅为 CFD计算所需时间的1/240，可以实现离心泵内流场的快速精确预估。

2.2 内流场模态分析

依据1.3节流场基模态分析方法，将由网格节点坐标及流场参数构成的快照集减去平均快照集，并进行奇异值分解，最后叠加平均快照集，得到基模态流场，如图7～10所示。

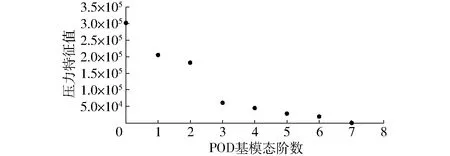
图7 各阶POD模态对应的压力特征值Fig.7 Pressure eigenvalue of POD modal

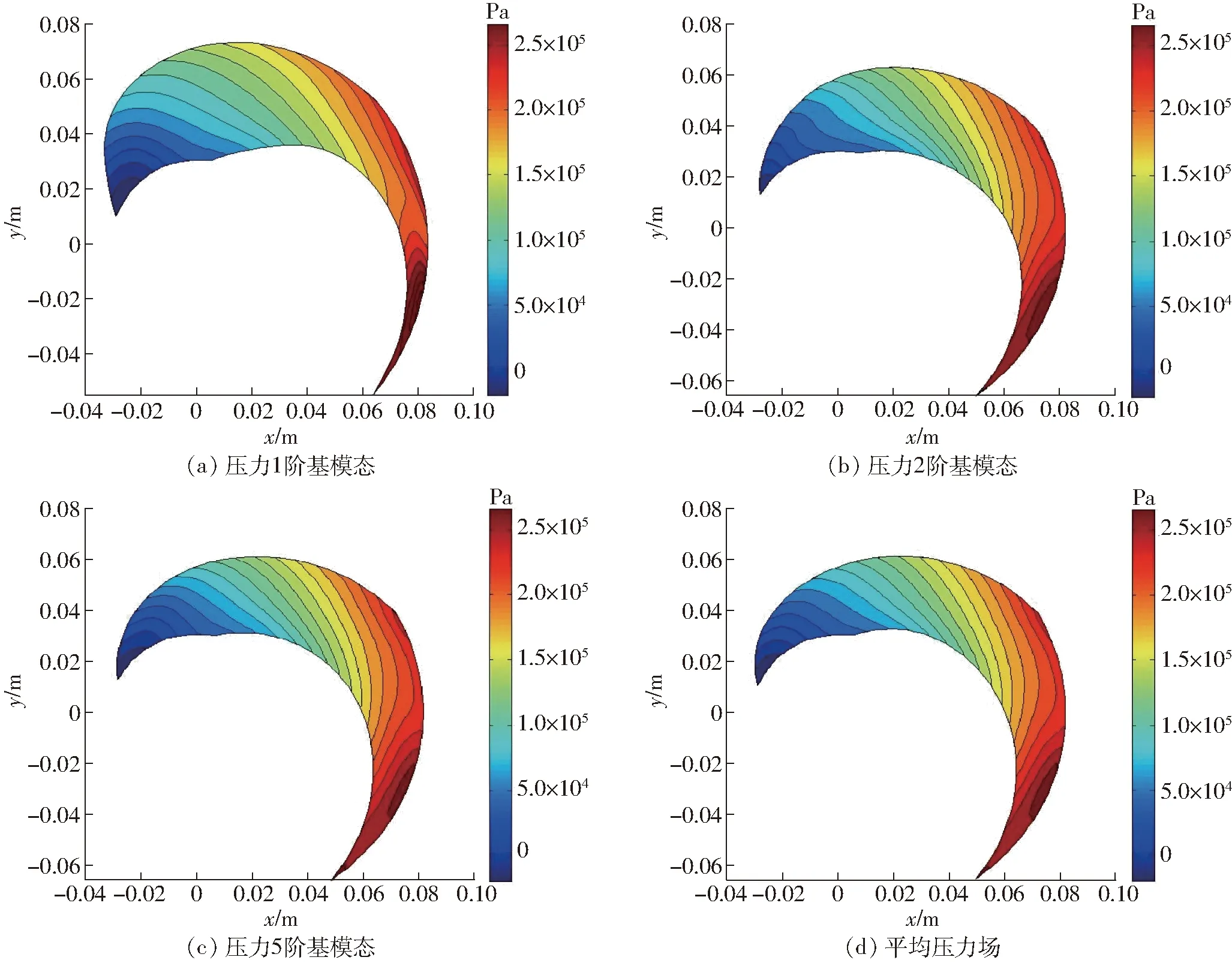
图8 基模态压力流场Fig.8 Pressure field of base modal

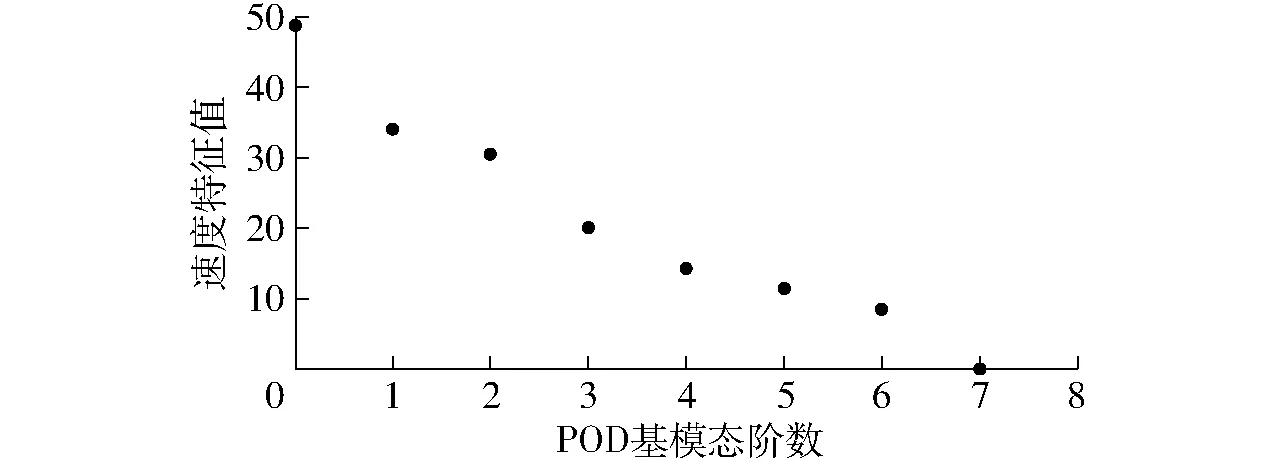
图9 各阶POD基模态对应的速度特征值Fig.9 Velocity eigenvalue of POD modal

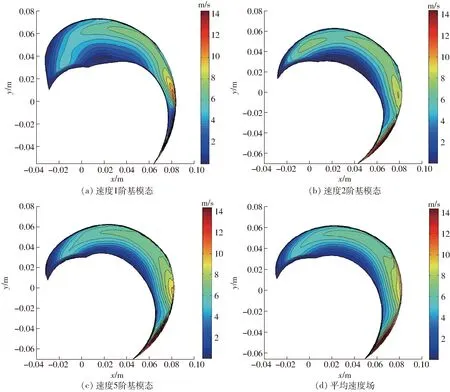
图10 基模态速度流场Fig.10 Velocity field of base modal

图7、9分别为压力场与速度场的各个基模态特征值分布，由图可以看出随着基模态阶数的增多，其所包含的特征越少，前6阶压力与速度的基模态分别包含了其97.7%、94.9%的流场能量。图8及图10分别是基模态压力场与基模态速度场，从中可以看出，第1阶POD基模态流场与样本平均流场的差异最显著，说明其包含的流场变化特征最多，第5阶基模态流场与平均流场基本一致。由图8可以看出，压力第1阶基模态反映其进口到出口压力递增以及叶片压力面出口高压区的流场特征，压力第2阶基模态能够反映叶轮出口与隔舌的干扰引起的高压区特征。由图10可以看出，速度的第1阶基模态能够反映叶片压力面的低速区、叶片进口背面的低速区、叶片压力面出口低速区及叶轮出口与隔舌的干扰作用引起的高速区流场特征，第2阶基模态反映出叶片出口压力面附近的高速区特征，其余的速度场特征相比于第1阶基模态明显减弱。

3 结论

(1)提出了采用POD-RBF混合代理模型方法对离心泵叶轮内流场进行重构分析。从对离心泵叶轮内流场的重构分析结果来看，POD-RBF方法能够精确重构出其压力场与速度场分布的结构特征，压力预测均方根误差为0.84%，速度预测误差基本在0.5 m/s以内。

(2)对样本集进行POD基模态分析，前6阶基模态基本包含所有流场能量，1阶基模态流场与样本平均流场差异最显著，说明其包含的流场变化特征最多，5阶基模态流场与平均流场基本一致。采用POD基模态分析可以精确地预测叶轮内流场的流动特征。

(3)提出的POD-RBF方法能够快速精确地对低比转数离心泵叶轮内流场进行重构，流场预估所需时间约为CFD计算的1/240，并可精确捕捉到内流场的分布特征，其预测精度高、计算量小，可以作为代理模型用于流体机械优化设计中流场的预估。