钙质土中重力串锚水平承载力特性有限元研究❋

徐保照, 李 飒, 苏洪路

( 1.天津港东疆建设开发有限公司, 天津 300463; 2.天津大学建筑工程学院, 天津 300072; 3.天津二建建筑工程有限公司, 天津 300143 )

近几十年来，海洋油气资源的开发成为现在能源开发的热点，海洋油气的开发促成了越来越多海洋平台的建造逐步向深海发展。中国海域面积广阔，土质的分布也比较特殊，从一般的粘土、砂土到与粘土和砂土性质不同的迭层土[1]，再到易破碎的珊瑚礁、钙质砂以及硬的钙质岩(礁灰岩)，每种土都有各自的特殊性，钙质土中的钙质砂与一般的粘土及砂土最大的不同是，钙质砂在受力的情况下，表现出颗粒易碎、强度、压缩及循环荷载下强度衰减等特性,在该土质条件下需要慎重选择锚固基础。

重力锚是一种应用比较早的锚固形式，主要靠自重下锚底与土之间的摩擦力来提供反力[2]，其结构简单，由混凝土块或碎金属或其他高密度材料制成。对于含有礁灰岩的钙质土，重力锚可以较好地适用于这种土质条件。在国外有不少学者对重力锚进行了相关的研究，Taylor R[3]设计了带剪力键的重力锚，给出了重力锚在粘土中的承载力计算公式。Harris R E等[4]为波浪能转换器(WECs)设计锚泊系统，讨论了该体系所遇到疲劳荷载和磨损以及从工程造价和土质适用上探讨了传统的锚泊系统对该体系的适用性，得出的结论是重力锚是比较优越的。Taylor R等[5]介绍了热带岛屿或者火山环礁附近海域上的海洋热能转换器(OTEC)可能的锚固设计方案，根据环境条件，设计了拖曳嵌入式锚和带有裙翼的重力锚，并探讨其外形尺寸的选择。Michael G S[6]为东南佛罗里达海洋再生能源体系设计了重力锚泊系统，主要设计了单锚的外形尺寸并进行了强度验算。Jim B. Petersen[7]发明了用锚链连接在一起的两个或者多个锚单元，用来增加锚抓力；同时，锚单元在安装过程中可以转动，以确保锚以正确的方向安装在海底。Ben U[8]在华盛顿州的SR520常青点浮桥和西雅图登陆项目设计中，因地制宜地设计了轴钻锚(Drilled shaft anchor)、重力锚、抓锚三种不同的锚来适应不同的工况条件。在国内，李怀亮等[9]对重力锚水平承载力进行了相关的研究。对于钙质土的研究，近年来不少学者做了相关的研究[10-13]。

1 模型的可靠性验证

1.1 理论计算

为了对串锚进行相关分析，首先需要对建立的计算模型进行可靠性验证。重力锚的结构示意图如下：

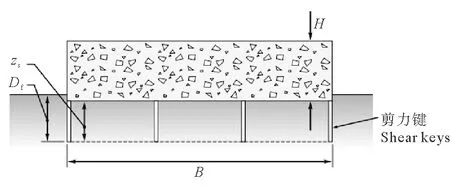
图1 重力锚结构示意图Fig.1 The structure diagram of gravity anchor

此图为锚的断面图，锚主体为长方体型，即蹲块式重力锚，重力锚有安装剪力键和无剪力键的情况，各个物理参数在下面进行详细说明。

模型的验证采用如下方法进行：分别用理论及室内模型试验和有限元法计算重力锚的水平极限承载力，然后对比三种方法的计算结果，如果有限元计算的结果和理论计算以及室内试验结果的误差在容许的范围内，则认为模型是可靠的，反之则不可靠。目前相关规范[2]给出，在非粘性土中，锚在水平荷载作用下，锚底土体发生排水剪切破坏，水平极限承载力按下式计算：

Qul=μ[(Wb+γbADf-Fve)cosβ-Fhsinβ]+Rp。

(1)

式中：Qul为锚水平极限承载力；μ为锚底与土体的摩擦系数或者是在有剪力键的前提下土与土之间的摩擦系数，计算公式为μ=tan(φ-5°)(在没有剪力键的钢质或混凝土的锚底需要折减5°，有剪力键则不用折减)；Wb为锚在水下的重力；Fve为设计荷载与锚链荷载在竖直方向上的分力(竖直向上为正)；Fh为设计荷载与锚链荷载在水平方向上的分力(沿锚底坡向方向为负)；γbADf为剪力键间土体的浮重；γb为土的浮重度； A为锚底面积；Df为剪力键入泥深度(海底泥面以下为正)；β为海底泥面坡角；φ是锚底土体内摩擦角；Rp为锚底前沿的被动土压力，Rp可由下式计算：

(2)

式中Kp为被动土压力系数，计算公式为：

Kp=tan2(φ/2+45°)。

Talory对式(1)进行了简化，当β=0时，

Qul=μ[(Wb-Fve)]+Rp。

(3)

对于平底锚(无剪力键)，在水平荷载作用下，公式(3)可简化为

Qul=μWb。

(4)

此次验证采用单个重力锚，并且没有锚底的剪力键。对于重力锚下面土体的计算相关参数，可以根据室内试验结果。采用室内试验方法对钙质砂的成分进行测试。样本的钙质砂中CaCO3含量都大于95%，钙质砂的重度为19 kN/m3。试验用钙质砂的颗粒级配见图2，采用此级配的钙质砂在不同的相对密实度下进行直剪试验，得到钙质砂内摩擦角随相对密实度变化的关系见图3。根据上述试验结果，确定重力锚下土体的计算参数。

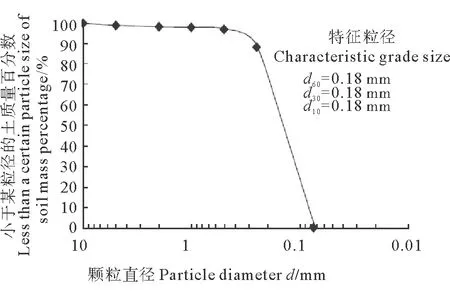
图2 钙质砂的颗粒级配Fig.2 The particle gradation of calcareous sand

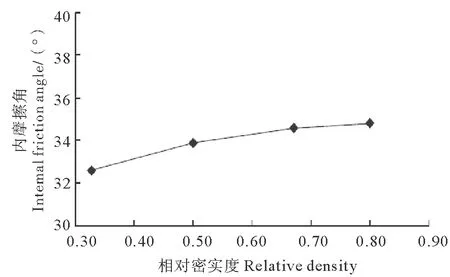
图3 钙质砂内摩擦角随相对密实度的变化关系Fig.3 The relationship of internal friction angle and relative density of calcareous sand

1.2 有限元模型建立

为了分析重力锚的水平承载机理，采用有限元方法对承受水平拉力的重力锚进行分析。计算采用ABAQUS 有限元软件，土体单元类型采用C3D8R 实体单元，土体的计算范围根据锚体的外形尺寸确定，计算深度与计算宽度均取约为5倍锚的相应高度和宽度以消除边界的影响，土体尺寸选定为20 m × 20 m × 10 m(长×宽×高)。土体采用M-C(摩尔-库伦) 本构模型，土重度取19 kN/m3(浮重度9 kN/m3)，内摩擦角取35°，相当于密实钙质砂的内摩擦角，弹性模量30 MPa，泊松比0.25。为了提高模拟精度，土体单元采用渐进加密的单元划分。重力锚干重84.78 t，锚的尺寸为3.0 m×3.0 m×1.2 m，对于重力锚尺寸的要求相关规范[2]有详细说明，其材质为钢材，其本构模型采用性弹性体，其密度为7 850 kg/m3(考虑重力锚在海底受到浮力，计算时采用水下密度6 850 kg/m3)，弹性模量取2.1×105MPa，泊松比0.3。

重力锚与土体之间设置接触面，接触面采用surface-to-surface 类型，在接触属性定义切向和法向接触面特性，对于切向特性，平底锚采用土体内摩擦角折减5°取正切；对于法向特性，采用硬接触。土体底部约束三个方向上的位移，四周立面约束水平方向上的位移。在计算分析过程中，均考虑重力锚应用于悬链线式系泊系统，即重力锚只承受水平荷载，Fve = 0，海底地面平坦，即β = 0，水平力施加在锚前面形心位置。

根据提取的锚上水平反力和位移对应关系，可绘制有限元法所计算的重力锚水平极限承载力-位移图见图4。

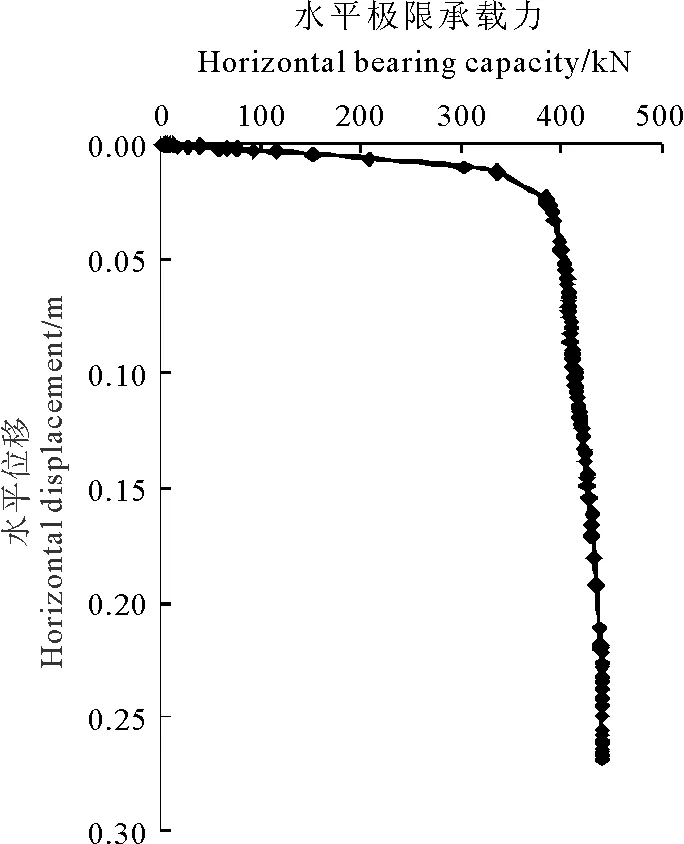
图4 单锚位移-水平极限承载力关系Fig.4 The relationship of displacement-horizontal bearing capacity of single gravity anchor

从上图可以看出，重力锚在水平荷载作用下，锚底土体发生滑动破坏，图中水平位移-承载力关系曲线有明显的拐点，从图中可得到重力锚的水平极限承载力为390.201 kN。

1.3 模型试验

重力锚构件尺寸为3.0 m×3.1 m×1.2 m。模型几何比尺为1∶15，所以重力锚模型试件尺寸取：0.20 m×0.20 m×0.10 m。试验装置由流速控制系统、量测系统、计算机数据采集系统等几部分组成。试验过程基本原理为：设定水流流速，通过调节变频电动机转速从而改变水泵流量，同时在管道内布置毕托管检测实际流速，直到达到水槽设定水流流速。重力锚后端布置拉线式位移传感器，监测重力锚运动；在重力锚前端的缆绳上布置拉力传感器。待水流流速平稳后，利用数据采集器将传感器上的信号传送到电脑上。本次试验主要通过水压加荷。通过定滑轮在水槽末端悬挂一塑料水箱，利用水泵向水箱内匀速加水，实现对重力锚试件的匀速加载。

试验过程按照相关的规范[14-17]操作进行，锚静止在水槽钙质砂上，等土中超静水孔压完全消失后，开始均匀施加水平荷载，至锚移动后触发行程开关，加载停止，锚在水平荷载下移动一定距离后将停下(见图5)，此时可认为锚下面土体已破坏，由于水流速度很小，对锚的阻力很小，可以忽略，故锚移动以前的荷载为锚水平承载力极限值。

图5 锚在水平荷载作用下滑动破坏Fig.5 Sliding failure of gravity with horizontal load

根据计算机采集的数据，将锚的水平荷载和位移关系绘制如下图。

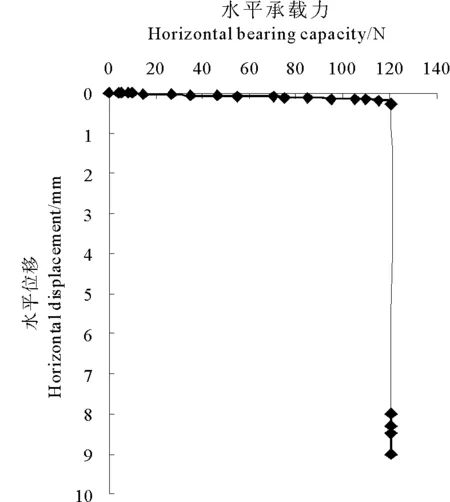
图6 锚位移-荷载关系Fig.6 The relationship between the displacement and horizontal bearing capacity of gravity anchor

从图中可以看出，水平荷载与位移的关系曲线有明显的转折点，水平极限承载力为120.21 N。

模型试验中锚的总干重25.004 kg，按照相似三定理的关系，原型锚的质量为84.38 t，按公式(4)可计算得模型锚水平极限承载力为125.87 N，有限元计算的结果也按相似三定理换算，其结果为115.62 N，相对误差分析见下表1。

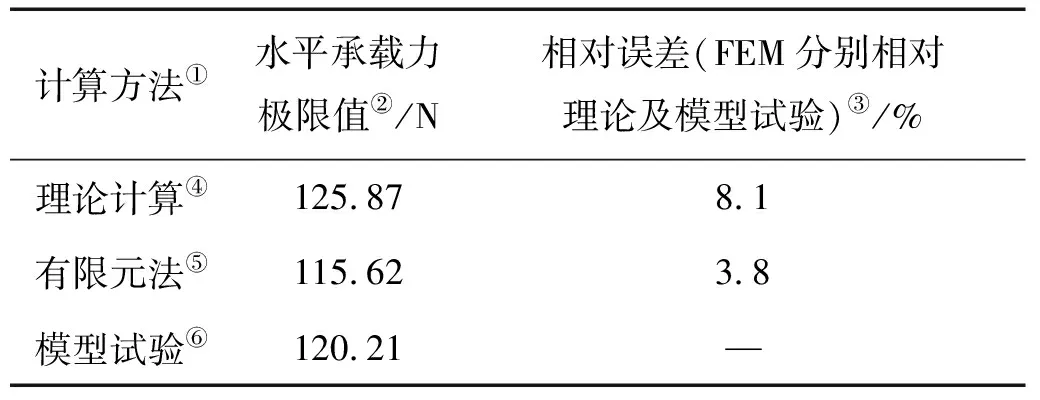
表1 不同方法所得锚水平极限承载力Table 1 horizontal ultimate bearing capacity of gravity with different method

Note：①Computing method；②Horizontal ultimate bearing capacity；③Relative deviation (FEM compared with theoretical and model test respectively)；④Theoretical calculation；⑤Finite element method；⑥Model test.

从表中可以看出，不论是与理论计算还是模型试验结果相比，有限元法所计算结果的相对误差都在10%以内，因此，可以确信有限元模拟计算的结果是可靠的。

2 串锚承载力机理特性

串锚是将多个重力锚单元用锚链串联起来，本次主要研究由两个重力锚单元串联起来的串锚承载力特性，两个锚单元的尺寸仍采用上面重力锚的尺寸，锚链的长度分别为10、20、40、60和80 m，计算的土质条件仍不变，对应土体尺寸分别为40 m×20 m×10 m、 60 m×20 m×10 m、80 m×20 m×10 m、100 m×20 m×10 m、120 m×20 m×10 m。计算模型见下图：

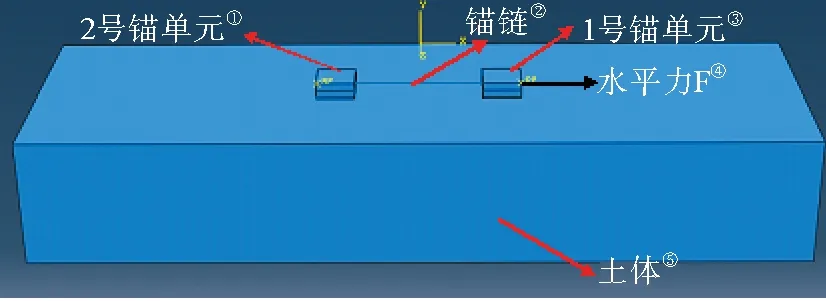
(①2# anchor unit；②Anchor chain；③1# anchor unit；④Horizontal force；⑤Soil.)

图7 串锚有限元模型示意图
Fig.7 Finite element model of multiple gravity anchors

在ABAQUS中，锚链常用truss单元来模拟，truss单元为桁架单元，所有的单元的节点均为铰接点，只有平动自由度，这就意味着truss单元没有转动方向的刚度，只能受拉或受压。对于本次模拟的锚链，只受拉，故可以用truss单元来模拟，锚链的等效截面积为0.007 85 m2，本次研究的锚链材质为钢质，锚链直接与前后两个锚立面形心连接以简化计算模型，连接方式为锚链两端的节点与前后锚单元的立面耦合(Coupling)。为了模拟可操作性以及横向可对比性，锚链的初始状态均为刚好绷直(相对水平荷载，锚链自重可以忽略)。水平荷载施加在1号锚前面形心位置，与单锚情况相同。分别提取1号锚单元受力点的水平荷载和位移，绘制水平荷载和位移关系图如下图所示：

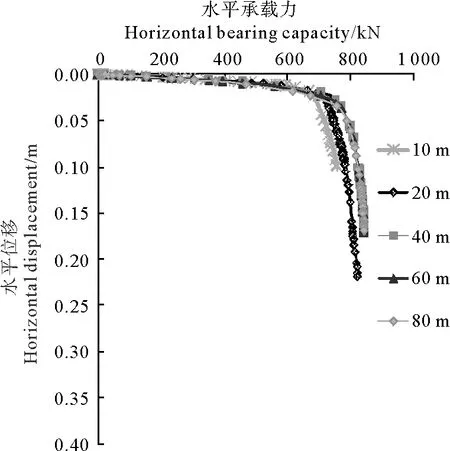
图8 不同锚链长度的串锚水平承载力与水平位移关系

从上图可看出，串锚的水平承载力与位移关系和单锚类似，图中所有曲线有明显的拐点，锚链长度为10 m的串锚水平承载力最小，从图中可以得到不同长度的锚链的串锚水平承载力，见下表2。

表2 不同锚链长度的串锚水平承载力与水平位移Table 2 the relationship between horizontal bearing capacity and displacement with different length of chain

注：锚链长度为10 m的串锚水平极限承载力小于700 kN，故水平反力为700 kN时锚底土体已破坏，和其他工况的串锚水平位移没有比较意义。

Note:①Chain length of multiple anchors；②Horizontal ultimate bearing capacity；③Horizontal displacement under horizontal ultimate bearing capacity；④Horizontal displacement under horizontal reaction 700 kN.

很明显，总体对比起来，随锚链的长度增加，串锚的水平承载力有增加的趋势，当锚链达到一定长度，承载力基本不变，总体上来讲，锚链越长，串锚达到水平极限承载力时发生的位移也越大，达到同样的水平承载力时，同样锚链越长，锚发生的位移越大。对比单锚和串锚水平承载力，见下表3。

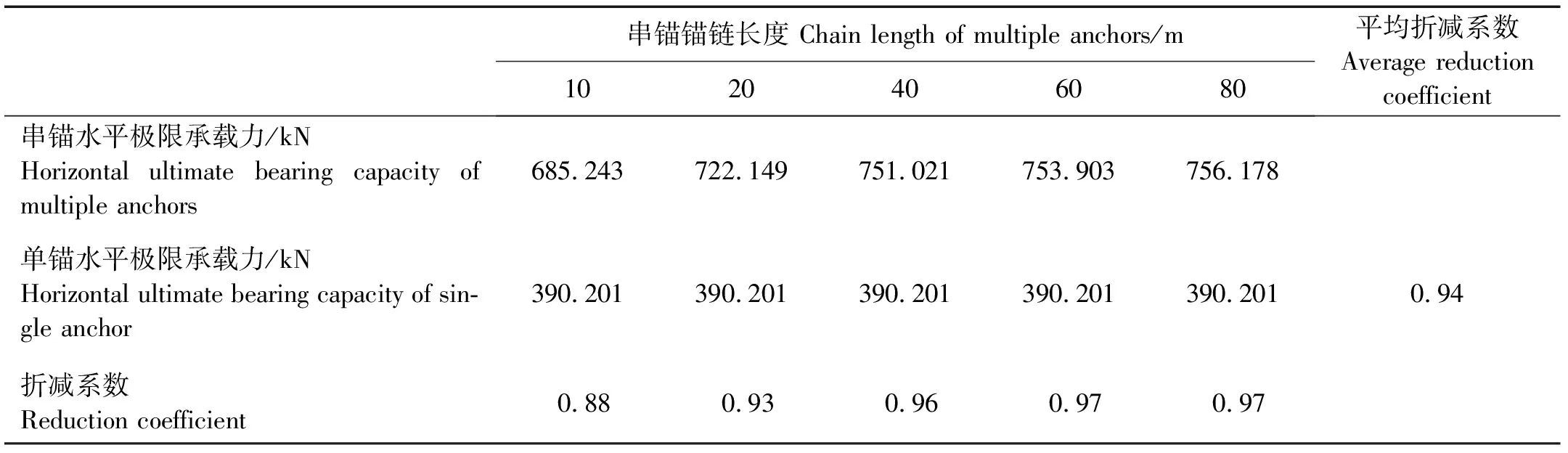
表3 串锚承载力与单锚对比Table 3 the horizontal bearing capacity of single gravity anchor and multiple gravity anchor

注：这里的折减系数是串锚水平承载力与单锚水平承载力2倍的比值。

Note:Reduction coefficient=Horizontal ultimate bearing capacity of China anchor÷(Horizontal ultimate bearing capacity of single anchor ×2).

从上表3可以看出，所有串锚的水平承载力均小于单锚水平承载力的2倍，也就是说串锚的承载力不是单个锚承载力的简单相加，造成这种情况的原因可以从水平承载力机理上解释。

首先可以研究单锚承载力机理，下面两个图为单锚在水平荷载作用下发生滑动破坏后土体的等效塑性应变云图(PEEQ)和塑性屈服图(AC YIELD)。

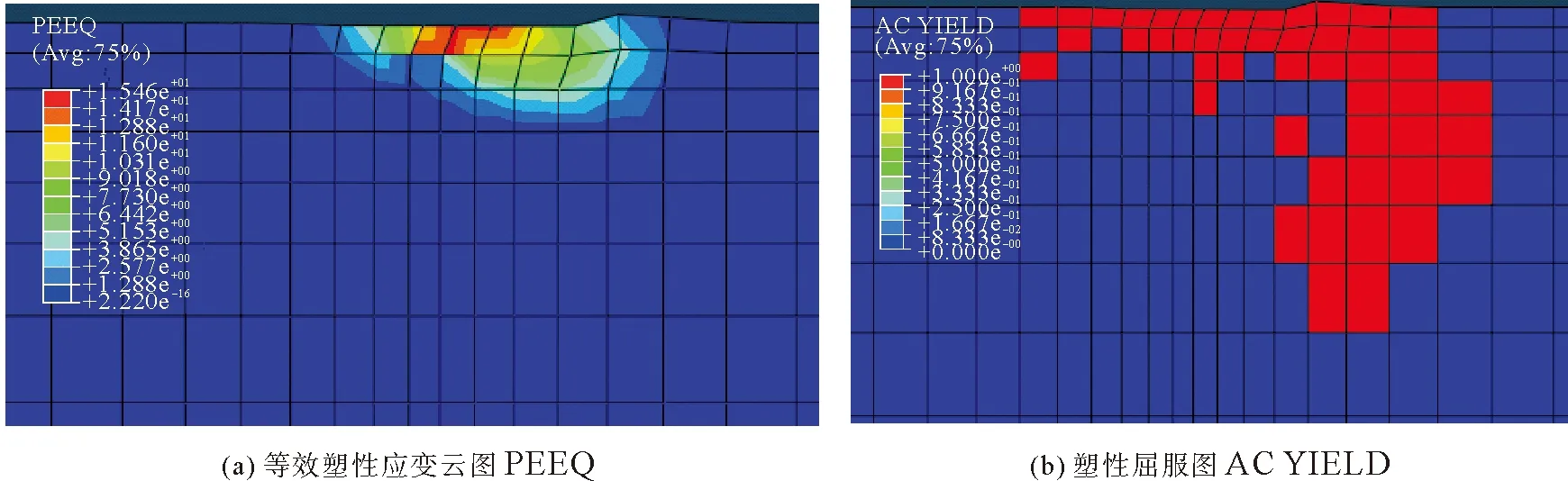
图9 单锚锚底土体等效塑性应变云图和塑性屈服图Fig.9 PEEQ and AC YIELD of the soil under single gravity anchor

上面的剖面是沿锚水平轴线纵向剖开，荷载施加方向为水平向右。为了清楚看到土体破坏后各项指标，故将锚移除。从上图可以明显看出，在水平荷载作用下，锚底土体发生滑动破坏，破坏面为弧形，靠近前端，破坏面较深。

图10分别是锚链长度10、20、40、60和80 m串锚锚底土体等效塑性应变云图。图10均是右边是1号锚锚底土体，左边是2号锚锚底土体，由于土体过于狭长，只截取了锚底一定范围内的土体。

从上图(a)到(e)可看出，串锚的每个锚单元破坏模式基本上和单锚相同，都是锚底土体发生滑动破坏，不同的是，前面的锚单元锚底土体塑性应变值较后面的锚单元大，破坏面也较后面的大；随着锚链长度的增加，这种差距变的较小。其原因是：在水平荷载作用下，由于锚链的存在，每个锚单元受力是不一样的，前面的锚单元受力大于后面的锚单元，也就是说，随着水平荷载作用的增加，前面的锚单元会先发生锚底土体滑动破坏，导致水平滑动失效，随后将力传给后面的锚单元，后面的最后也发生滑动破坏。因此导致串锚的水平承载力不是单个锚水平承载力相加。对于不同锚链长度的串锚，在一定范围内锚链越长，破坏时前面锚单元发生的位移越大，这样后面的锚单元能够充分发挥承载力效应。

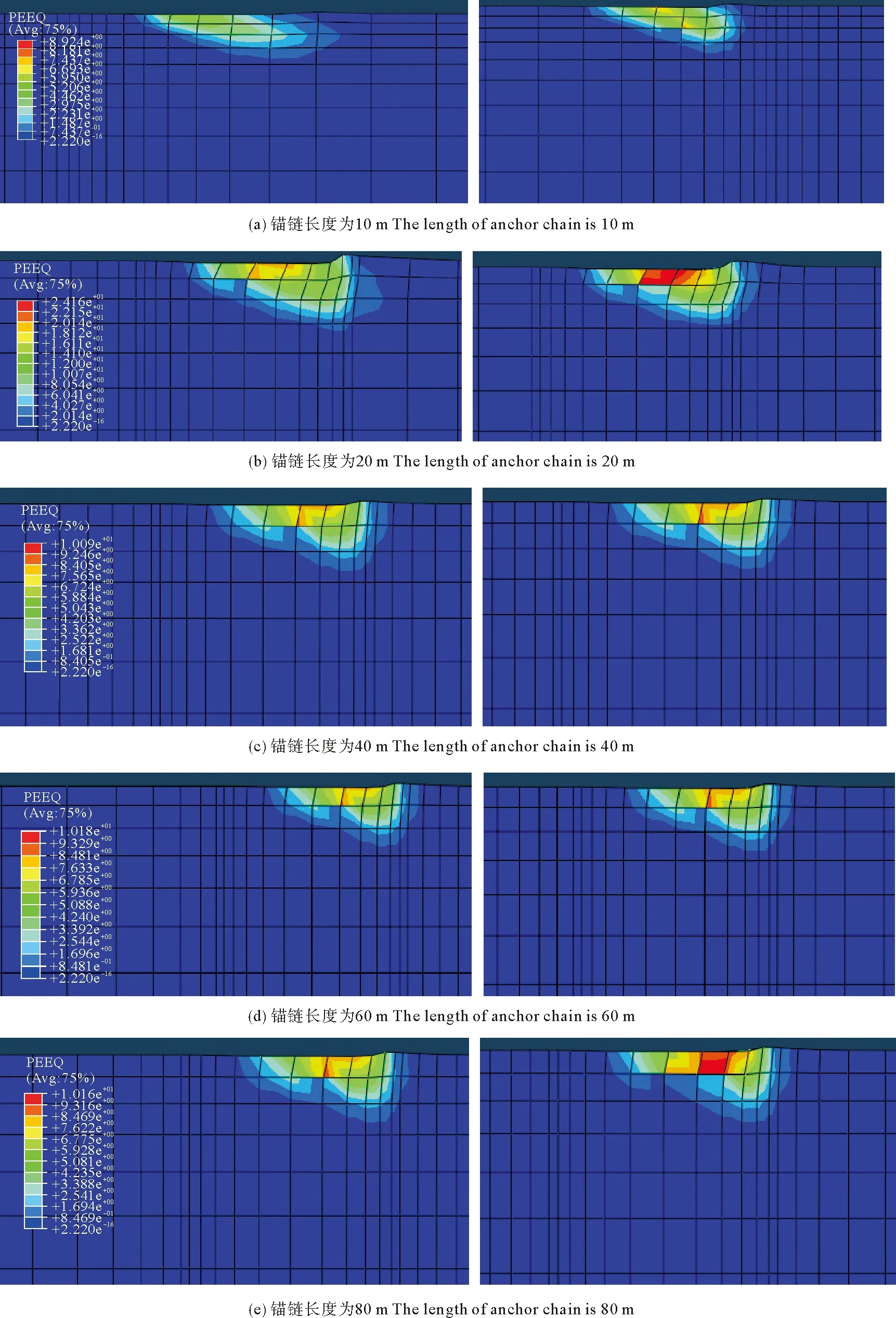
图10 不同锚链长度串锚锚底土体等效塑性应变云图Fig.10 PEEQ of the soil under multiple gravity anchor with different chain length

3 结论

通过有限元对串锚在水平荷载作用下破坏过程的模拟，可以得出下面几点结论：

(1)串锚在水平荷载作用下，首先是前面施加荷载的锚单元先发生滑动破坏，随后是后面的锚单元发生滑动破坏，即前面锚单元受力较后面的大，滑动破坏模式和相应的单锚基本相同。

(2)串锚的水平承载力与锚链长度有关，在一定范围内，增加锚链的长度可以提高串锚的水平承载力，超过某一长度后，锚链的长度对串锚的承载力影响不大。

(3)串锚的水平承载力不是单个锚的水平承载力相加，其水平承载力小于相应的单个锚水平承载力之和，在进行串锚水平承载力设计计算时应给与适当的考虑。

针对串锚的破坏模式以及锚链长度对水平承载力的影响，在此文的参考下，需要用模型试验来进一步确认锚链最佳长度，这正是下一步所要做的研究工作。