改进窗函数下的忆阻器特性分析和研究
(河南理工大学电气工程与自动化学院,河南焦作454000)
1971年,美国加州大学伯克利分校的蔡少棠教授首次提出忆阻器的概念[1]。2008年惠普实验室的Strukov等[2]首次成功设计出忆阻器的物理模型。忆阻器不仅在理论模型方面[3-6],还在混沌电路、模拟电路、图像处理、神经网络等应用方面[7-9]都有着广泛的研究成果。
杂质漂移机理[2]在研究忆阻器导电过程及特性方面具有代表性,随之线性离子迁移忆阻器模型[2]也被首次提出,但是并没有很好地满足忆阻器的真实特性。窗函数对分析忆阻器的内部离子真实漂移规律起重要作用。为了更好地呈现其非线性效果,学者们在忆阻器数学模型中引入了窗函数。Joglekar等[10]、Yu等[11]窗函数尽管其大部分优势被保留下来,但存在 “边界锁死”问题,即当内部分界面运动到任意一端电极时,无论外部任何激励都无法改变内部离子的迁移。一旦 “边界锁死”发生,忆阻器的阻值就不再发生改变。Biolek等[12]模型因在窗函数中考虑到电流因素解决了 “边界锁死”问题,但该窗函数中的参数因为只能取正整数导致其可调性受限。Prodromakis等[13]解决了窗函数可调性受限问题,但忽略了 “边界锁死”问题。
为了解决上述窗函数各自存在的问题,本文提出了一种改进的窗函数模型,基于MATLAB软件工具,通过改变相关参数,分析并对比传统窗函数下忆阻器模型的滞回特性,不仅解决了 “边界锁死”问题,还具有可调性和高灵活性,同时还分析了不同频率下滞回特性曲线的变化规律。本文的研究为忆阻器的制造及应用奠定了理论基础。
1 线性杂质漂移忆阻器模型
1.1 忆阻器数学模型
图1为HP忆阻器物理模型。该模型由两端金属铂片电极Pt夹杂着两层钛氧化物薄膜组成,假设忆阻器模型总尺寸长度为D,其中掺杂了氧空缺的TiO2-x薄膜厚度为w,对外呈导电状态;另一层TiO2薄膜厚度则为D-w,对外呈绝缘状态。

图1 HP忆阻器物理模型Fig.1 HP memristor physical model
忆阻器的瞬时阻抗数学模型表达式:
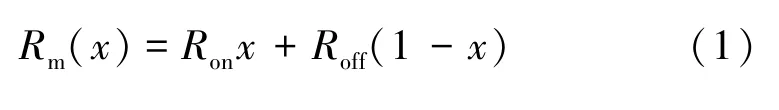
式中:x表示HP忆阻器的内部状态变量,[0,1];Rm表示HP忆阻器的总阻值;Roff和Ron分别表示w=0或者w=D时忆阻值的极限值。
偏置电压v(t)和流经忆阻器的电流i(t),与瞬时阻抗Rm之间满足欧姆定律:

HP实验室给出了分界面在杂质线性漂移情况下的移动规律[2]:

式中:μv表示平均离子漂移速率,是反映杂质在导电区域中移动能力的一个物理量。
1.2 杂质漂移机理(Dopant Drift Mechanism)
杂质漂移机理是在忆阻器模型掺杂区中氧空缺形成和迁移的基础上建立的。

图2 外加电场下掺杂区和非掺杂区杂质迁移图Fig.2 Doping and undoped impurity migration graph under applied electric field
当对忆阻器两端施加偏置电压v(t)时,流经其内部的电流为i(t)。在未掺杂层,氧化钛分子中每一个钛原子配有两个氧原子,并且它们之间用稳定的离子键连接,因此该氧化钛中的氧原子很难随意地移开。故未掺杂层被看作是对外绝缘而且没有电流流过。但在掺杂层,由于缺少一定比例的氧原子而形成氧空位,导致离子键的不稳定性,氧原子很容易在相邻的钛原子之间移动。氧空缺带有正电荷,因为同种电荷相互排斥,所以向外加电源的负极性端移动,电荷的定向运动形成电流。部分氧空缺进入或离开非掺杂区,从而改变了掺杂区和非掺杂区的厚度,忆阻器的瞬时阻抗也随之发生改变。
1.3 线性杂质漂移模型
图1中,线性杂质漂移模型的分界面在内部整个区域内是以匀速来回移动的,即状态变量x的匀速变化反映了内部离子线性运动。图3是基于1.1中的忆阻器数学模型表达式(1)~(3),搭建忆阻器线性漂移模型,通过MATLAB软件仿真出来的伏安特性曲线图。这里,忆阻参数设置:Ron=100 Ω,Roff=16 kΩ,忆阻器的电阻初始值R0=11 kΩ,ΔR=Roff-Ron,数学模型的初始值设为x0,x0=(Roff-R0)/ΔR=0.3145。

图3 线性忆阻器模型下的I-V特性曲线图Fig.3 TheI-V characteristic curve for linear memristor model
由于HP忆阻器是纳米级器件,实际应用中,在很小的压差下就会产生强大的电场,致使离子漂移受限,特别是靠近两端电极时表现更明显[14],这里将这种现象称为边界效应;另一方面,当分界面到达任一端电极时,会处于停滞状态,忆阻器的阻值将不再发生改变,这就是所谓的 “边界锁死”现象。
2 不同窗函数下的忆阻器特性分析
为了更加准确地模拟HP忆阻器内部离子的真实迁移情况,在公式(3)中引入了窗函数f(x),即:

2.1 Joglekar窗函数
忆阻器模型中常用的Joglekar窗函数定义[10]:

式中:x∈[0,1],p取正整数。从上述公式中可知,当x=0和x=1时,f(x)=0,则dx/dt=0,即当分界面到任一端电极时,任何外部激励都无法改变这种停滞状态,忆阻值将不再发生改变,因此,该窗函数下的忆阻器模型存在 “边界锁死”现象。
(1)参数p值的影响
在外加电压幅值U=1.2 V,频率f=1 Hz下,分别取不同的p值,对忆阻器的伏安特性进行分析,结果如图4所示。由图4得知,随着p值的增大,I-V特性曲线处于重叠状态。p值对特性曲线几乎没有影响。

图4 不同p值下I-V曲线图(U=1.2 V,f=1 Hz)Fig.4 TheI-V curves at differentp(U=1.2 V,f=1 Hz)
(2)外加电压的影响
图5所示,在f=1 Hz,p=2条件下,随着电压幅值的增大,I-V滞回曲线包围的面积也随之增大。由于该窗函数模型存在 “边界锁死”问题,在x∈[0,1]区域内,当电压U→∞时,I-V曲线趋于不光滑,不能很好地实现忆阻器的非线性漂移。

图5 不同电压幅值下I-V曲线图(f=1 Hz,p=2)Fig.5 TheI-V curves at different voltage(f=1 Hz,p=2)
2.2 Biolek 窗函数
为了解决 “边界锁死”问题,Biolek窗函数将电流作为一个重要的因素考虑在内,其定义[12]:

式中:x∈[0,1],p取正整数,stp(·)为窗函数中关于电流i的符号函数:。
该窗函数中考虑到了电流因素,使得忆阻值变化不会受 “边界锁死”的影响,即忆阻值会随着电荷的运动情况做出相应的变化。
但是参数p与Joglekar窗函数中的参数取值一样,只能取正整数,取值范围受限;当x∈[0,1]时,该窗函数的最大值fmax恒等于1,因此不能保证该窗函数的可调性。
(1)参数p值的影响
对比Joglekar窗函数下相应的I-V特性曲线图4和图5,相同电压幅值和频率情况下,图6中I-V曲线随着p值的增大显示出明显的滞回特性。

图6 不同p值下I-V曲线图(U=1.2 V,f=1 Hz)Fig.6 TheI-V curves at differentp(U=1.2 V,f=1 Hz)
(2)外加电压的影响
图7中,在f=1 Hz,p=2条件下,随着电压幅值的增大,I-V滞回特性曲线包围的面积也随之增大,并且有明显的非线性。
没有控制参数致使该窗函数的可调性受限,当电压增大到一定值时(U=6 V),忆阻器便失去了滞回特性,这是因为该忆阻器模型中内部离子漂移运动在此电场作用下出现了畸形导致忆阻器被击穿,如图8所示。
2.3 Prodromakis窗函数
为了更好地突显内部杂质迁移的非线性和函数可调性,Prodromakis窗函数给出了很好的解决方法,该窗函数中因含有控制参数j,可控制该窗函数的大小,即分别在f(x)<1和f(x)≥1范围内变化,Prodromakis窗函数定义[13]:
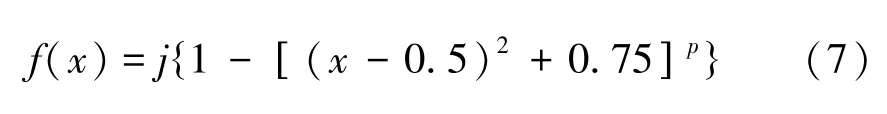

图8 电压U=6 V下I-V曲线图(f=1 Hz,p=2)Fig.8 TheI-V curve atU=6 V(f=1 Hz,p=2)
式中:x∈[0,1],p为正整数。不考虑控制参数j的情况下,通过选择合适的p值,该窗函数的最大值fmax在区域(0,1)内变化,而Biolek窗函数的最大值fmax恒为1,显然保证了窗函数的可调性。
(1)参数p和j的影响
图9是在U=2 V,f=1 Hz,j=1条件下,分别取不同的p值仿真出来的。随着p值的增大,I-V滞回特性曲线包围的面积增大,选取合适的p值,会显示明显的非线性,当p值趋于无穷大时,将与理想的线性漂移模型很接近。

图9 不同p值下I-V曲线图(U=2 V,f=1 Hz,j=1)Fig.9 TheI-V curves at differentp(U=2 V,f=1 Hz,j=1)
图10,在U=2 V,f=1 Hz,p=2条件下,随着j值的增大,I-V滞回特性曲线包围的面积增大,其非线性越明显。最重要的是,j值的调节使得f(x)不仅仅只在f(x)<1范围内变化,所以运用比较灵活。并且发现j值的变化与外加电压幅值变化对忆阻器伏安特性影响规律基本一致。

图10 不同j值下I-V曲线图(U=2 V,f=1 Hz,p=2)Fig.10 TheI-V curves at differentj(U=2 V,f=1 Hz,p=2)
(2)外加电压的影响
图11,在U=6 V左右,斜 ‘8’字滞回特性曲线并没有变形,曲线也很光滑。保持I-V曲线不失真情况下,相比前两个窗函数下的对应曲线,该窗函数下忆阻器模型的外加电压幅值范围比较大。
选择该窗函数既可以更好地建立非线性忆阻器模型,调节合适的参数还可以创建线性模型。但同Joglekar窗函数模型一样存在 “边界锁死”问题。

图11 不同电压值下I-V曲线图(f=1 Hz,j=1,p=2)Fig.11 TheI-V curves at different voltage(f=1 Hz,j=1,p=2)
2.4 一种改进的窗函数
综上三种传统窗函数下的忆阻器伏安特性分析,本文提出一种改进的窗函数模型,该窗函数是在Biolek窗函数的基础上加上了控制参数j,不仅避免了 “边界锁死”,并且还具有可调性,其定义如下:

式中:x∈[0,1],p取正整数,stp(·)为该窗函数中关于电流i的符号函数:。
该窗函数仿真曲线如图12所示(j=1)。

图12 不同p值下的改进窗函数曲线图形(j=1)Fig.12 The improved window function curves at differentp(j=1)
(1)参数p和j的影响
图13与Biolek窗函数下的忆阻器模型仿真图6对比,在j=1的情况下,参数p值对忆阻特性的影响是一致的,即:随着p值的增大显示出明显的滞回特性。
图14中,该窗函数因含有控制参数j,增加了可调性,使得f(x)调节范围没有局限性;并且随着j值的增大,I-V滞回曲线包围的面积增大,滞回特性更加明显,反映了该模型下内部离子非线性漂移的变化规律,根据不同的参数变化作相应的调整,便于实际电路中的应用。在电压允许范围内,j值的变化间接扩大电压幅值范围。
通过调整相关参数p和j的值,该窗函数同样也可以创建线性杂质忆阻器模型。

图13 不同p值下I-V曲线图(U=1.2 V,f=1 Hz,j=1)Fig.13 TheI-V curves at differentp(U=1.2 V,f=1 Hz,j=1)

图14 不同j值下I-V曲线图(U=2 V,f=1 Hz,p=2)Fig.14 TheI-V curves at differentj(U=2 V,f=1 Hz,p=2)
(2)外加电压的影响
图15与图7和图8对比,外加电压幅值范围增大,另外,在U=6 V时,该窗函数下的伏安特性并没有失真,并且具有很完整的非线性和滞回特性。反映了该窗函数下的忆阻器模型在较高的电压下不会被击穿,内部离子漂移运动还可以做非线性变化。

图15 不同电压值下I-V曲线图(f=1 Hz,j=0.6,p=2)Fig.15 TheI-V curves at different voltage(f=1 Hz,j=0.6,p=2)
该窗函数下的忆阻器模型由于考虑到电流的影响,不存在 “边界锁死”问题,还可以通过控制参数j值的变化,扩大外加电压幅值范围,具有可调性和高灵活性。
2.5 上述窗函数相关参数对照
表1中,不难发现本文中改进的窗函数下的忆阻器模型的伏安特性更具有优越性,既解决了边界效应和 “边界锁死”问题,还具有可调性和高灵活性,其伏安特性仿真结果与忆阻器内部离子实际迁移规律更相符。改变控制参数可使得忆阻特性更好地呈现出来。

表1 不同窗函数下影响参数对照表Tab.1 A comparison of performance factors for different window functions
3 频率对忆阻器滞回特性的影响分析
当施加一个正弦交流激励i=sin(ωt)时,忆阻器的当前电荷量设为q0,并且电荷存储公式q=q0-(1/ω)cos(ωt)。当ω逐渐增大时,电荷q→q0。忆阻器的阻值会在很小的范围内(q0-1/ω,q0+1/ω)变化,当ω→∞时,忆阻值会变成一个常数。
为了分析不同频率下忆阻器伏安特性的变化规律,设置不同频率值,通过MATLAB软件得出仿真图16。

图16 不同频率下I-V曲线图(U=4 V,j=1,p=2)Fig.16 TheI-V curves at different frequency(U=4 V,j=1,p=2)
随着频率的增大,I-V曲线包围的面积呈现缩小状态。频率的增大,实际上是电压周期缩短,离子迁移在很短时间内做往返运动,则忆阻值的变化范围不会很明显,当频率f→∞时,伏安曲线会缩减成一条直线,忆阻值趋于一个定值,忆阻器就等同于一个普通的电阻元件。
4 结论
为了更加准确地模拟HP忆阻器内部离子的真实迁移情况,基于杂质漂移机理,分析了忆阻器的导电过程,提出了一种改进的窗函数模型。通过对比分析传统窗函数下忆阻器模型的伏安特性,改进的窗函数模型由于考虑到电流方向的影响及其范围的局限性,不仅解决了 “边界锁死”问题,还具有可调性和高灵活性。在频率允许范围内,随着频率的增大,忆阻器的伏安特性会呈现缩减趋势,且当频率趋于无穷大时,会变成一个单值函数,忆阻器等同于一个普通的电阻元件。通过调整该窗函数模型的相关参数,也可以创建一个理想的线性杂质漂移忆阻器模型。

