关于Pell方程ax2-by2=±1没有正整数解的证明

李勇

关于Pell方程2-2=±1没有正整数解的证明

李勇

广安职业技术学院师范学院, 四川 广安 63800

关于Pell方程的正整数解问题，国内外学者进行了广泛的讨论。本文以2-2=±1为例，通过两种解法得出10个定理，并分别进行证明，结论如下：两种解法都假设(mod 20)为素数，第一种解法当1 (º±3,±7)、-1 (º±3,±7)、-1 (º-1,-3,-7,-9)、1 (º-1,-3,-7,-9) 时，Pell方程都没有正整数解；第二种解法当1 (,Î+,º±1,±9)，且(p/)=-1 (=1,2,…2+1)时，当1 (,Î+,º±3,±7)，且(p/=-1 (=1,2,…)时；当-1 (,Î+,º1,9)，且(p/)=-1 (=1,2…2+1)时；当-1 (,Î+,º-3,-7)，且(p/)=-1 (=1,2,…,)时；当-1 (,Î+,º3,7)，且(p/)=-1 (=1,2,…,)时；当=-1 (,Î+,º-1,-9)，且(p/)=-1 (=1,2,…2)时，Pell方程都没有整数解。

Pell方程; 正整数解; 取模

Pell方程（佩尔方程）属于不定二次方程的一种类型，它在数学领域有着广泛的应用，例如Pell方程结合欧几里得算法，可以对某个正整数平方根的近似值进行计算。早在古希腊时期，著名数学家阿基米德就提出了二元二次不定方程，可以看成Pell方程的前身。十六世纪，法国数学家费马进一步探索了该类型方程在求解方面的问题，他对Pell方程正整数解的无穷性进行了猜测，但还未很好地证明[1]。同时代的英国数学家沃利斯则解决了Pell方程正整数解无穷性证明这一问题[2]。广泛意义上的Pell方程存在着两种类型：（1）2-2=(,,Î)；（2）2-2=±1,±2,±4 (,,,Î,¹0。随着数学理论的不断发展，Pell方程有了更完善的理论基础，而且在实际应用方面也被挖掘出更多的价值，影响到人们生产生活的方方面面。本文主要对2-2=±1这一例Pell方程没有正整数解的问题进行探索。

1 Pell方程ax2-by2=±1的相关定理

1.1 第一种解法的定理

设的模值为，=±5,º±1,±3 (mod 10)，为素数，有以下4个定理：

定理1：方程2-(-5)2=1 (º±3,±7 (mod 20)为素数)，没有整数解。

定理2：方程2-(+5)2=-1 (º±3,±7 (mod 20)为素数)，没有整数解。

定理3：方程2-(-5)2=-1 (º-1,-3,-7,-9 (mod 20)为素数)，没有整数解。

定理4：方程2-(+5)2=1 (º-1,-3,-7,-9 (mod 20)为素数)，没有整数解。

1.2 第二种解法的定理

设=,Î+, 5|,º±1,±3 (mod 10)为素数，为合数，有以下6个定理：

定理5：方程5px2-2=1 (,Î+,º±1,±9 (mod 20)为素数)，p是素数，且(p/)=-1 (=1,2,…2+1)没有整数解。

定理6：方程52t+1px2-2=1 (,Î+,º±3,±7 (mod 20)为素数)，p是素数，且(p/)=1 (=1,2,…)没有整数解。

定理7：方程5px2-2=-1 (,Î+,º1,9 (mod 20)为素数)，p是素数，且(p/)=-1 (=1,2,…2+1)没有整数解。

定理8：方程52t+1px2-2=-1 (,Î+,º-3,-7 (mod 20)为素数)，p是素数，且(p/)=1 (=1,2,…)没有整数解。

定理9：方程52tpx2-2=-1 (,Î+,º3,7 (mod 20)为素数)，p是素数，且(p/)=1 (=1,2,…)没有整数解。

定理10：方程5px2-2=-1 (,Î+,º-1,-9 (mod 20)为素数)，p是素数，且(p/)=-1 (=1,2,…2)没有整数解。

2 Pell方程ax2-by2=±1相关定理的证明

2.1 第一种解法定理的证明

因此在º±3,±7 (mod 20)的时候，5/=-1，这与之前的设定产生矛盾，因此定理1没有正整数解。

定理2的证明：对于定理2中的方程，在方程的两边取模，-52º-1 (mod)，5/=1，但是前面证明在º±3,±7 (mod 20)的时候，5/=-1，同样产生了矛盾，因此定理2没有正整数解。

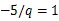
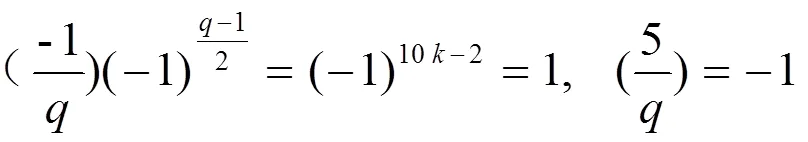
因此在º-1,-3,-7,-9 (mod 20)的时候，-5/=-1，这与之前的设定产生矛盾，因此定理3没有正整数解。

定理4的证明：对于定理4中的方程，在方程的两边取模，-52º1 (mod)，-5/=1，但是前面证明在º-1,-3,-7,-9 (mod 20)的时候，-5/=-1，同样产生了矛盾，因此定理4没有正整数解。

2.2 第二种解法定理的证明

又因为(p/)=-1 (=1,2,…2+1)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理5没有正整数解。

又因为(p/)=1 (=1,2,…)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理6没有正整数解。

又因为(p/)=-1 (=1,2,…2+1)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理7没有正整数解。

又因为(p/)=1 (=1,2,…,)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理8没有正整数解。

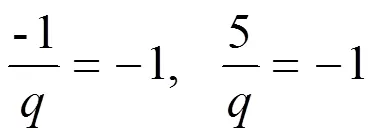
又因为(p/)=1 (=1,2,…)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理9没有正整数解。

又因为(p/)=-1 (=1,2,…2)，所以取模后的方程解为-1，这与之前取模后的方程解产生矛盾，因此定理10没有正整数解。

3 讨论

关于Pell方程正整数解的相关研究，国内外学者进行了大量的探索。美国数学家Pletser在探索2-2=±1是否存在可解性的过程中，给出了该类型方程没有正整数解的六个结论，他认为这样的结论对于狭义Pell方程的研究起到了重要作用[3]。英国学者Beck通过Legendre符号以及同余性质的运用，对Pell方程2-2=±1这一类型有无正整数解进行了探索，得出该类型方程没有正整数解的四个结论[4]。国内学者过静等人探讨了两类Pell方程组的解，得出结论：2-32=1，2-2=1这两个方程组不存在正整数解，只有平凡解[5]。本文针对Pell方程2-2=±1是否存在正整数解，给出了两种算法的10个定理，这些定理都不存在正整数解，并分别对这些定理进行证明。相对于国内外相关研究来说，本文的探索进一步拓展了该类型方程没有正整数解的结论，有一定的创新意义和应用价值。

4 结论

Pell方程没有正整数解这一命题自十六世纪以来，就一直处于广泛的讨论之中。本文以2-2=±1这一狭义Pell方程为例，对第一种解法假设 (mod 20) 为素数，用模代替，得出4个结论：当1 (º±3,±7)、-1 (º±3,±7)、-1 (º-1,-3,-7,-9)、1 (º-1,-3,-7,-9)时，Pell方程都没有正整数解；对第二种解法假设(mod 20)为素数，p是素数，在方程两边取模，得出6个结论：当1 (,Î+，º±1,±9)，且(p/)=-1 (=1,2,…2+1)时，Pell方程没有整数解；当1 (,Î+，º±3,±7)，且(p/)=-1 (=1,2,…)时，Pell方程没有整数解；当-1 (,Î+，º1,9)，且(p/)=-1 (=1,2,…2+1)时，Pell方程没有整数解；当-1 (,Î+,º-3,-7)，且(p/)=-1 (=1,2,…)时，Pell方程没有整数解；当-1 (,Î+,º3,7)，且(p/)=-1 (=1,2,…)时，Pell方程没有整数解；当-1 (,Î+,º-1,-9)，且(p/)=-1 (=1,2,…2)时，Pell方程没有整数解。

[1] Colman WJA. Some Remarks on the Pell Equation[J]. Mathematical spectrum, 2015(3):125-127

[2] Elsner C. On Exponential-type Sums Formed by Solutions of Pell's Equation [J]. Journal of combinatorics and number theory, 2014(3):163-181

[3] Pletser V. On continued fraction development of quadratic irrationals having all periodic terms but last equal and associated general solutions of the Pell equation[J]. Journal of Number Theory, 2014(12):339-353

[4] Jzsef B. Pell equation and randomness[J]. Periodica Mathematica Hungarica: Journal of the Janos Bolyai Mathematical Society, 2015(1):1-108

[5] 过静,赵建红,杜先存.关于Pell方程组~2-3~2=1与~2-~2=1的解[J].数学的实践与认识,2017(20):265-269

Proof of the Existence of No Positive Integer Solution for Pell Equation2-2=±1

LI Yong

63800,

The problem of positive integer solution of Pell equation has been extensively discussed by scholars at home and abroad. This paper takes2-2=±1 as an example, draws 10 theorems through two solutions, and proves them separately. The conclusion is as follows: both solutions assume that (mode 20) is a prime number. The first solution is when 1 (º±3,±7)、-1 (º±3,±7)、-1 (º-1,-3,-7,-9)、1 (º-1,-3,-7,-9), There is no positive integer solution to the Pell equation. The second solution is 1 (,Î+,º±1,±9), and (p/)=-1 (=1,2,…2+1), when 1 (,Î+,º±3,±7), and (p/=-1 (=1,2,…); when 1 (,Î+,º±3,±7), and(p/=-1 (=1,2,…); when -1 (,Î+,º-3,-7), and (p/)=-1 (=1,2,…,); when -1 (,Î+,º3,7), and (p/)=-1 (=1,2,…,); when 当=-1 (,Î+,º-1,-9), and (p/)=-1 (=1,2,…2), there is no integer solution to the Pell equation.

Pell equation; positive integer solution; take form

O122.2

A

1000-2324(2018)06-0998-04

10.3969/j.issn.1000-2324.2018.06.019

2017-12-06

2018-02-25

李勇(1982-),男,本科,讲师,主要研究方向为数学与应用数学. E-mail:yfc2222@163.com