顺层岩质边坡开挖变形特征模型试验研究

习朝辉，裴向军，穆成林，阳 博

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

随着国家经济的发展，我国的基础设施建设取得了长足的进步。在工程建设中，经常出现边坡开挖的情况，其中层状岩质边坡比较常见。层状岩质边坡稳定性问题是目前需要解决的重大问题。层状边坡的复杂岩体结构在不同开挖条件下的变形失稳模式具有多变性和多样性。国内外许多专家对于层状岩质边坡开挖后的稳定性进行了研究。文献[1]指出顺层岩质边坡易产生滑动变形，在岩质边坡中危害最大。文献[2-3]对不同岩层倾角的顺层岩质边坡变形破坏机制进行了研究。文献[4]通过底摩擦试验，对缓倾层状边坡变形破坏机制进行了研究。文献[5]以一公路边坡为研究对象，在室内建立相似模型对顺层岩质边坡开挖过程中坡内位移和应力变化规律进行了深入研究。目前的研究主要集中在岩层倾角变化对边坡的影响，关于开挖坡角对顺层岩质边坡稳定性及变形破坏特征的研究相对较少。因此，在现场查明研究区(贵州织金茶店乡)地质情况的前提下，通过大型框架模型试验研究顺层岩质边坡不同开挖角度的变形破坏全过程，分析边坡变形破坏机制，根据模型上布置的监测点产生的变形情况确定边坡破坏范围，为边坡开挖设计及支护提供参考。

1 工程地质条件

研究区位于云贵高原上的低中山区，四周共有13个高挖方边坡，坡脚高程 1 260 m，边坡最大高差约190 m，最小高差45 m。研究区处于溶蚀、侵蚀洼地内，地质条件复杂。边坡岩层倾向350°～5°，倾角20°～45°，岩层厚度0.05～2.00 m。边坡岩性从上至下依次为粉质黏土、强风化白云岩、中风化白云岩。在边坡岩层中间含有多层软弱夹层，厚0.01～0.06 m，强度较低，多呈可塑状态。软弱夹层成为控制边坡稳定性和变形破坏特征的主控结构面。坡体节理较为发育，主要有2组，产状分别为125°∠78°，220°∠76°，节理间距一般为0.05～0.15 m，张开度为微张～张开，多有泥质填充。整个坡体结构岩体较为破碎，风化严重。现场实测剖面见图1。

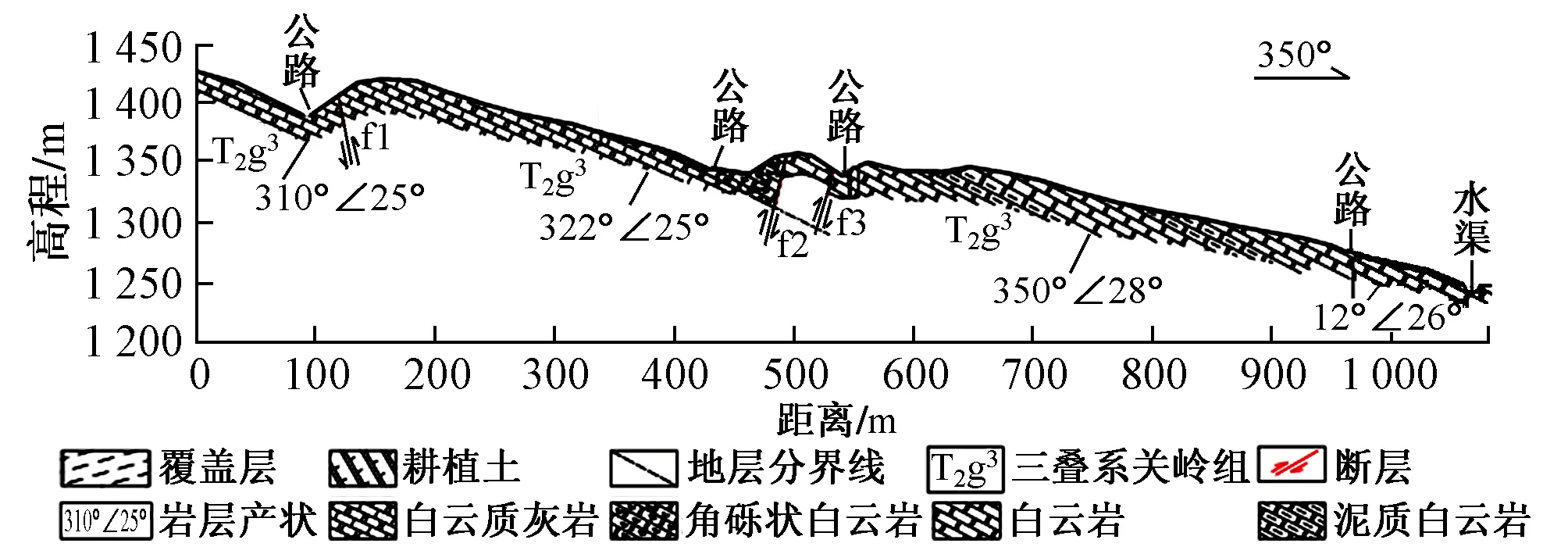
图1 现场实测剖面

2 模型试验

在工程地质研究中，采用物理模型试验去揭示和分析地质现象的本质是解决边坡变形失稳等问题的有效手段[6]。应用于开挖顺层岩质边坡分析具有几个突出的意义：①边坡变形破坏失稳在整个开挖过程中的演化特征能够直接再现；②可以通过试验监测数据分析边坡在开挖过程中位移与应力的分布及调整情况，为边坡演化机制等分析提供依据；③对于不同地质条件下的边坡可以多次试验，总结分析演化特征，对于同一地质条件的边坡可以采用差异的开挖条件以及外界影响因素来分析其变形及演化特征。

2.1 模型相似比确定

相似比是现场原型和室内模型之间具有相同量纲的物理量的比值[7]。本文采用二维室内框架模型试验，结合实际试验条件和原型边坡地质情况，建立室内物理模型。根据相似原理确定几何相似常数Cl=60，重度相似常数Cr=1.0。根据相似原理可以获得其他相关参数的相似比：Cσ=ClCr=60；Cl=Cδ=60；Cμ=Cε=Cf=Cφ=1；CE=CC=CRt=CRC=Cτ=55；Ct=(Cl)1/2=7.75。式中：Cσ为应力相似常数；Cδ为位移相似常数；Cμ为泊松比相似常数；Cε为应变相似常数；Cf为摩擦系数相似常数；Cφ为内摩擦角相似常数；CE为弹性模量相似常数；CC为黏聚力相似常数；CRt为抗拉强度相似常数；CRC为抗压强度相似常数；Cτ为抗剪强度相似常数；Ct为时间相似常数。

2.2 试验材料及配比

边坡模型采用具有一定厚度的试验块体搭建。试块制作采用预制模具压制而成。主要材料为水泥、石英砂、石膏和水。采用不同的材料配置强风化白云岩，中风化白云岩。试验材料的质量配比见表1。

表1 试验材料的质量配比

考虑岩层厚度的差异，采用 3种厚度来模拟不同的岩体，尺寸(长×宽×厚)分别为0.15 m×0.10 m×0.03 m；0.15 m×0.10 m×0.02 m；0.15 cm×0.10 cm×0.01 cm。根据现场调查结果，软弱夹层相似材料要具有强度低、遇水易软化等特点。经过反复试验研究，采取贵州高岭土掺加部分细颗粒河沙作为软弱夹层相似材料。

2.3 模型设计及试验步骤

试验模型箱内框尺寸(长×高×宽)为2.5 m×2.4 m×0.6 m，前无遮挡后有挡板。模块养护好之后，按照原始拟开挖边坡的坡型、坡体结构进行搭建。首先，在模型底部采用混凝土砖块搭建前低后高，岩层倾角25°的边坡作为基础，形成原始边坡倾斜岩层，然后依次铺设试块。在铺设过程中每一组的分界面铺设软弱夹层的相似材料。软弱夹层厚度设置为1～5 mm，尽量做到平整。软弱夹层模拟材料内摩擦角15°，黏聚力太小，可忽略不计。试验模型搭建完成以后需要静置6 h以上，待模型整体趋于稳定后，按照设计方案进行开挖。

在试验模型边坡标示拟开挖坡形线，由上至下依次开挖。每开挖一级后，位移计和压力计分别在30 min，1 h，2 h，4 h，8 h进行读数，直至监测数据稳定，再进行下一级开挖。此外，除了位移计监测外，在模型表面贴纸片，构成监测网，平行层面方向间隔0.15 m，垂直层面方向间隔0.10 m，在不利于布置位移计处进行监测，位移大小采用标尺直接测量，是对位移计的补充监测。

3 开挖方案设计

方案1：缓坡分级开挖。设计开挖坡角30°，每一级边坡高10.0 m，共9级，设计平台宽2.0 m，坡向为N，开挖高度90.0 m，SN向开挖，长170.3 m。设计图见图2(a)。

方案2：设计开挖坡角50°，每一级边坡高10.0 m，共9级，每3级设置1个宽10.0 m的平台，其余平台宽2.0 m，开挖高度90.0 m，SN向开挖，长107.5 m。设计图见图2(b)。

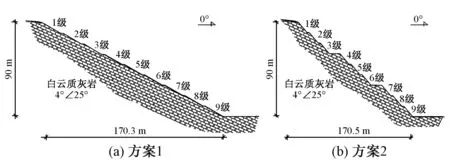
图2 开挖方案设计

4 试验过程与结果分析

4.1 试验过程

1)方案1

首先对边坡上部的1～3级坡进行开挖，开挖以后边坡未产生较为明显的变形。开挖4～6级坡后，可以观察到边坡产生了一定的变形，但整体位移较小，仅在6级坡的中下部至坡脚出现沿层面的滑动现象，其余位置则无明显位移。开挖7～9级坡后，在8级坡的坡脚出现18 mm的相对错动位移，相当于原始边坡的1.08 m，向下延伸长度为22 mm，相当于原始边坡的1.32 m。方案1变形破坏过程见图3(a)～(d)。

2)方案2

图3 变形破坏过程

开挖1～3级坡后,1级坡中上部及坡顶出现不同程度的裂缝，最大宽度15 mm，相当于原始边坡的0.9 m，在3级坡的坡脚存在层间错动迹象。开挖4～6级坡使得1级坡拉裂缝增宽，向坡体深处延伸。在3级坡的坡脚层间错动加剧，位移达50 mm，相当于原始边坡的3 m。模型中部出现裂缝，宽25 mm，向坡体内部延伸约46 mm。在6级坡的坡脚存在沿层面的相对错动迹象。开挖6级坡后，变形持续时间长达6 h。开挖7～9级坡后，1级坡拉裂缝宽度、深度持续增加，宽达42 mm，3级坡的坡脚相对位移68 mm，拉裂缝持续增宽，向坡体深处延伸。7～8级坡出现不同程度的拉裂变形。方案2变形破坏过程见图3(e)～(h)。

4.2 试验边坡变形破坏演化过程

对方案2从边坡开挖至变形破坏整个演化过程分析得出：①边坡以陡倾角(50°)开挖，首先在1级坡中部出现宽度较大的拉张裂缝，1～3级坡岩体沿层面向下滑动；②边坡变形失稳模式为由上及下、由表及里渐进失稳，尤其是在降雨后层间软弱夹层软化，强度降低致使边坡变形速度增大，失稳破坏特征明显；③对含多层软弱夹层的顺层边坡采用陡倾角(50°)开挖时变形失稳范围较大，破坏深度可达开挖面以下15～35 m，为深层失稳破坏。边坡破坏后从坡顶到坡脚出现多级滑动面。

4.3 试验结果拟合分析

图4 开挖边坡失稳范围预测模型

为了计算简单对试验模型进行了简化。开挖边坡失稳范围预测模型如图4所示。其中：H为开挖边坡的总高度，取1.50 m；h为计算高度到坡脚的垂直距离；h0为软弱夹层的间距，取5.5 cm；α为岩层倾角，取25°；β为开挖边坡坡角，取30°，50°；Lh为距坡脚垂直高度h的坡面上一点A距坡体内部失稳边界的水平距离。A为开挖边坡坡面上的点,B为坡体内部失稳边界上的点，A，B两点距X轴的垂直距离均为h，坐标分别为A(x1，y1)，B(x2，y2)。

x1=h/tanβ,y1=h

(1)

x2=h/tanβ+Lh，y2=h

(2)

部分试验参数统计见表2。

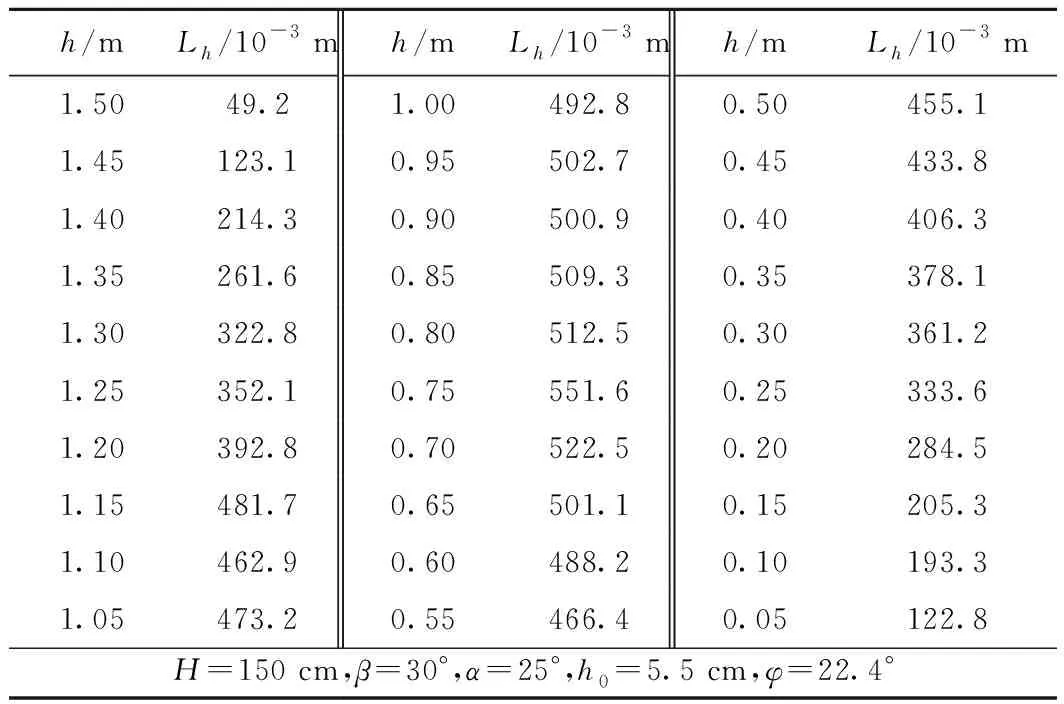
表2 部分试验参数统计

根据表2、图4可知:B点的轨迹在剪出口附近(M点前)近似于直线，M点后近似于指数函数。当x≤70 cm时，采用直线拟合效果较好;当x>70 cm时，使用指数函数进行拟合效果较好。因此可建立关于y轴的分段函数F(x)。

(3)

式中：a1，b1，a2，b2，c为由α,β,h0,H确定的常数。

由于数据较多，且公式复杂，故采用MATLAB计算软件反复进行多次拟合。将表2数据代入式(1)、式(2)中求得x，y的值，再将x，y的值代入式(3)中，拟合求得a1，b1，a2，b2，c的值。

(4)

5 结论

2)边坡形成阶梯状滑动面，说明边坡破坏在多层软弱夹层之间同时进行。边坡变形不是一次产生的，在最终失稳破坏前有多次的滑动现象。

3)顺层岩质边坡变形失稳范围与开挖坡角有关。开挖坡角30°时边坡破坏主要集中在4～7 m深处，开挖坡角50°时边坡破坏集中在15～35 m深处。在施工时应采用缓坡角开挖。