砂土地层深埋盾构隧道开挖面稳定性分析
张明聚,万 涛,李鹏飞
随着城市地下交通网络的形成,新建隧道的埋深越来越大,深埋盾构隧道也日渐增多,如何在盾构掘进过程中控制开挖面的稳定性是一个重要课题。在隧道开挖面稳定性分析中所采用的理论方法主要为极限平衡法和极限分析法。极限分析法因计算过程复杂在工程中应用受限,极限平衡法对土拱效应的考虑不够完善,导致其计算结果与实际相差较大,尤其是对砂土地层深埋盾构隧道开挖面极限支护力的计算。本文对此进行深入分析。
1 深埋盾构隧道开挖面失稳破坏模式
由文献[1-6]中砂土地层盾构隧道开挖面稳定性模型试验和数值模拟结果可以总结得到砂土地层深埋盾构隧道开挖面失稳破坏模式,如图1所示。图中:C为隧道埋深;D为隧道直径;σs为作用在地面上的超载;σT为作用在开挖面上的支护压力。在开挖面前方隧道顶部以下的土体为剪切滑动破坏;而在隧道顶部以上的土体因受土拱效应的影响,出现一定高度、近似垂直的剪切带,即该区域两侧的土体抗剪强度得到充分发挥。同时,在剪切带上方则出现一定高度的潜在塌落土体区域,该区在隧道掘进方向的垂直截面上近似呈抛物线状。值得注意的是,开挖面达到极限支护力时,隧道顶部以上土体主应力方向发生明显偏转。

图1 砂土地层深埋盾构隧道开挖面失稳破坏模式
2 开挖面稳定性分析的力学模型
文献[7-8]采用活板门模型试验来研究土拱效应。试验结果表明,土体相对滑移的大小将导致不同的土拱表现形态。因此,本文在砂土地层深埋盾构隧道开挖面极限支护力计算中作如下假设:在隧道顶部以上一定高度范围内由于土体相对滑移较大,土拱表现为矩形拱,矩形拱的两侧为剪切带;在矩形拱以上一定高度范围内由于土体相对滑移较小,土拱表现为曲线拱;2种形式的土拱在不同埋深处共同发挥作用,使得开挖面前方隧道顶部以上土体应力重分布。

图2 砂土地层深埋盾构隧道开挖面稳定性分析力学模型
根据砂土地层深埋盾构隧道的开挖面土体破坏模式以及根据土拱不同表现形态所作的假设,使用极限平衡法建立了砂土地层深埋盾构隧道开挖面稳定性分析力学模型,如图2所示。图中:在隧道顶部以下,滑动破坏土体为楔形体;ω为楔形体前端滑动面与水平面之间的夹角;L为楔形体顶部在隧道掘进方向的长度;B为楔形体顶部的宽度,B=0.25πD;根据文献[7]中的建议将曲线拱的形状假设为抛物线形,矩形拱和抛物线拱的高度分别为Hre,Hpa。
3 开挖面极限支护力计算
3.1 抛物线拱对土压力的传递
与文献[7]中的方法一致,本文假设抛物线拱的土体破裂面呈抛物线状,破裂面以上土体自身成拱,并且将上方土体中的一部分土压力传向下方两侧土体中;矩形拱以上至抛物线状破裂面以下区域为潜在塌落土体区域。假设抛物线状破裂面以上土体对下方土体的竖直压应力为σvr。经抛物线拱对土压力重分布以后,作用在矩形拱顶部的有效竖直荷载V由2部分组成:抛物线拱以下的土体自重W和竖直压应力σvr所对应的土压力Pv。为求解σvr,在紧邻抛物线状土体破裂面上方土体中取一个抛物线形土拱微元体,如图3所示。

图3 抛物线拱荷载传递机制
该微元体的厚度为dh,过抛物线拱两端的切线与水平方向的夹角为θ,拱高为f,f= (Ltanθ)/4=L/(4tanφ)。假设θ=90°-φ,φ为土体的内摩擦角[8]。同时,将作用在抛物线拱微元体上的土压力等效成均布荷载q,作用在整个跨度上。
经过抛物线拱对土压力重分布以后传递到两侧相邻不动土体上的竖直应力σv1近似等于静止土压力γ(C-Har)减去抛物线状破裂面以上土体对下方土体的竖直压应力σvr。其中:γ为土体重度;Har为土拱整体高度。由于抛物线状破裂面以上土体共同成拱发挥作用,实现了土压力的重分布,因此
(1)
抛物线拱微元体在均布荷载q作用下的侧向推力dFh[9]为
(2)
作用在抛物线拱拱脚上的水平应力σhr=dFh/dh,假设σhr作用在拱底部,其值是个常数,且沿土拱微元体厚度方向均匀分布。由式(1)和式(2)可得水平应力
(3)
由应力莫尔圆可得A点处竖直压应力σvr与水平应力σhr的关系为
将式(3)代入式(4)得
(6)
抛物线拱以下的土体自重W为
(7)
因此,作用在矩形拱顶部的有效竖直荷载V为
(8)
作用在矩形拱顶部的平均应力qm为
(9)
3.2 矩形拱两侧的剪切带高度
本文统计了多个典型开挖面稳定性模型试验及数值模拟结果,得到了隧道顶部以上矩形拱两侧的剪切带高度Hre和矩形拱两侧剪切带之间宽度L的值,见表1。
首先计算了宽度L与高度H之间的比值η=L/H,然后将η、λ=tan(45°-φ/2)及其相对偏差进行比较,结果见图4。相对偏差δ的计算公式为
(10)
由图4可知:η与λ值较为接近,各组η与λ的相对偏差δ介于0.3%~11.0%。

表1 剪切带高度和宽度统计结果
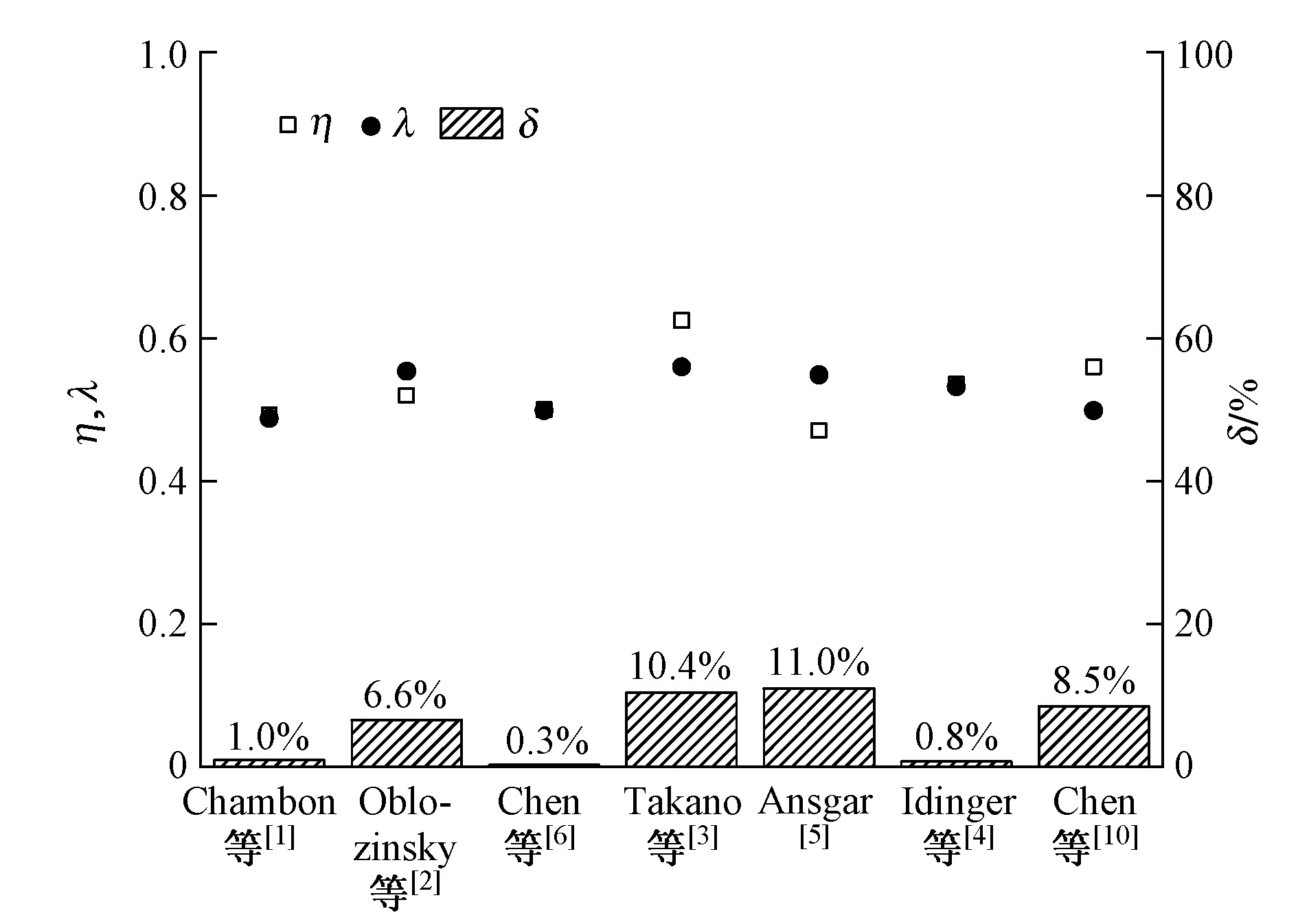
图4 剪切带宽高比η、(45°-φ/2)的正切值λ、相对偏差δ的对比
当隧道埋深较大且开挖面处于极限支护力状态时,可由式(11)近似得到隧道顶部以上矩形拱两侧的剪切带高度Hre。
(11)
3.3 开挖面极限支护力
开挖面极限支护力的计算分析如图5所示,楔形体的重力G为
G=(π/8)γD3cotω
(12)

图5 开挖面极限支护力的计算分析
根据太沙基松动土压力理论[11],在矩形拱高度范围内距地表任意深度z处取一个厚度为dz的无穷小微元体。该微元体在竖直方向受力平衡,可得矩形拱底部竖向应力σav为
式中:Kc为矩形拱两侧的土体侧压力系数,当土体抗剪强度充分发挥时,Kc=(1+KaKp)/(Ka+Kp)[12],Ka为主动土压力系数,Kp为被动土压力系数。
作用在楔形体两侧滑动面上的摩擦力T2为
(15)
土拱的整体高度Har=Hre+Hpa,其中Hpa=L/(4tanφ),Hre由式(16)确定,其中L=D/tanω。
(16)
对楔形体在水平方向和竖直方向上分别进行受力平衡分析,求得隧道开挖面处极限支护力P为
(17)
隧道开挖面处极限支护力P除以隧道截面面积S即可得到开挖面处极限支护压力plim。
(18)
式中:η1=tan(ω-φ)/tanω-K0μtanφ;η2=tan(ω-φ)/(2tanω)-(K0μtanφ)/3;μ=(4/π)[cotω+tan(ω-φ)]cosω,ω∈[π/4,π/2);K0为静止土压力系数,K0=1-sinφ。
4 算例分析
为了验证本文计算模型的准确性,以文献[1]离心机模型试验中的工况为例进行分析,并与本文计算方法和一些经典理论方法[13-16]所得结果进行对比。在文献[1]中隧道直径D为10 m,土体重度γ为 16.0 kN/m3,土体内摩擦角φ介于38°~42°。由文献[1]离心机模型试验结果可知:埋深比C/D分别为2和4时开挖面极限支护压力分别为8.0 kPa和8.2 kPa;当埋深比C/D>2时,归一化极限支护压力几乎不再随着埋深的增大而增大。

图6 离心机模型试验与各理论方法所得开挖面极限支护压力对比
取内摩擦角φ的2个极值38°和42°,计算结果见图6。本文计算方法与其他经典理论方法和模型试验所得结果一致,即当隧道埋深比C/D>2时,归一化极限支护压力几乎不再随着埋深的增大而增大。
在相同埋深条件下,极限平衡法(文献[13]、文献[14]和本文计算方法)得到结果明显大于极限分析法(文献[15]、文献[16]),但是极限分析法的计算过程较为复杂,且隧道顶部以上的计算模型并不能反映开挖面的土体破坏特征。本文计算方法所得结果明显小于文献[13]楔形体模型计算结果。当隧道埋深不断增大时,由于文献[14]没有合理考虑矩形拱上方的土压力,导致其计算结果过于保守,而本文计算方法所得结果与离心机模型试验结果(文献[1])和极限分析法(文献[15-16])所得结果较为接近。因此,从总体上来看,本文提出的计算模型用于开挖面前方土体破坏特征分析合理,计算精度较高,同时计算过程较为简单,可满足工程需求。
5 结论
1)通过对砂土地层深埋盾构隧道开挖面的失稳破坏模式的分析以及土拱效应的现有研究,根据土拱形态随隧道埋深变化作出假设:在隧道顶部以上一定高度范围内土拱呈矩形拱;在矩形拱以上一定高度范围内土拱呈曲线拱;2种形式的土拱在不同埋深处共同发挥作用,使得开挖面前方隧道顶部以上土体实现应力重分布。
2)基于该假设,修正了Terzaghi松动土压力计算公式,建立了砂土地层深埋盾构隧道的开挖面处极限支护压力计算方法,该方法可以反映深埋盾构隧道开挖过程中土拱效应。通过算例分析,本文提出的计算方法对开挖面前方的土体破坏特征分析合理、计算精度较高,同时计算过程较为简单,可满足工程需求。

