铁路客票快速经由算法的研究与实现

张 霞，单杏花，戴琳琳，尹伊伊

（中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081）

近年来，中国交通运输行业高速发展，特别是高铁成网后，高速列车和动车组列车开行密度逐渐增大，为广大旅客的出行提供了很大的便利。但是，随着旅客出行数量的增长，有些问题也日益突出。其中，站点与站点之间的可达性问题成为困扰旅客出行的主要因素，具体来说，旅客在通过网络进行购票时，经常会遇到始发站与终点站间没有直达车次或直达车次没有余票的情况，此时，旅客往往只能自行选择换乘站，再查询是否有始发站到换乘站以及换乘站到终点站的车次，这一过程操作复杂，耗时巨大，且旅客单靠人力根本无法全面掌握始发站与终点站间的多个换乘线路，进而往往无法选择合适的换乘站。并且，在春运等时间段，还很有可能遭遇所选的换乘站也没有余票的情形，这导致旅客的出行极为不便。车站发售通票的功能也仅限于路径规划[1]。因此，如何自动为旅客提供有效的换乘方案，成为目前亟待解决的技术问题。

在此背景下，本文中的铁路客票经由算法是指，在给定列车发站X和到站Y的情况下，基于中转次数、运行里程、时间、总票价和中转代价等因素，向旅客提供推荐列车中转线路的算法。

如果将一趟列车从起始站到终点站看作一个有向直线，沿途各站为该有向直线的各点，那么经由算法可以转化为有向图的最短路径算法。同时，所有停靠站都可以很容易地转化为某种唯一编号，铁路的经由算法就转化为基于N个节点的有向图，计算两个节点之间的最短（最优）路径的问题[2]。这里，N为沿途的车站数。

文中所述的基于经由算法的最短路径算法，是指换乘次数最少条件下的最短（最优）路径，再辅以考虑里程、时间和票价等综合评分因素，为旅客提供最合理的出行的接续方案。因此简单的图论最短路径算法不能满足经由算法的实际应用需求。

1 简单的图论算法

简单的图论算法就是通过有向图广度搜索（BFS）或深度搜索（DFS），把出发点i至到达点j的所有路径找出，然后列出最短路径。在搜索过程中，需要排除回路，即经过出发点之后不能再回溯到i，且达到终点j则停止并返回。

简单的图论算法中，线路信息即为有向图，有向图可以通过邻接表（Adjacency List）或邻接矩阵（Adjacency Matrix）来描述图中各个节点之间的连通属性，其中，邻接表使用顶点及其所邻接的边来表示，而邻接矩阵使用N×N的数组来表示各点间的连通性。图论算法的效率问题直接取决于数据结构的存储结构及方式，使用邻接表，时间复杂度为O(N+e)，e为常量；而使用邻接矩阵，时间复杂度为O(N2)。

简单经由算法只能找到路径最短的经由通路[3]，对于实际客票经由问题，还需考虑列车票价、中转次数等，显然不是客票经由算法的最佳选择[4]。客票经由不是简单的径路问题，需要考虑车次实际开行情况[5]。本文基于传统的经典图论算法并结合铁路实际业务，提出快速经由算法。

2 经由传递闭包

2.1 传递闭包

在数学概念中，在集合X上的二元关系R的传递闭包是指包含R的X上的最小的传递关系。从定义上很容易看出，对于经由算法来说，集合X就是所有停靠站的集合，关系R就是任意两个停靠站之间是否有列车直达，即可用邻接矩阵表示，那么R的传递闭包（简称：经由传递闭包）就是任意两个停靠站间是否最终可达。

引入经由传递闭包是为了检验给定的两个停靠站是否最终可达。在快速经由算法中，根据经由传递闭包中两个停靠站的可达状态，决定是否继续计算相关中转站，它是减少无效节点计算的有力方法。

2.2 弗洛伊德算法

计算传递闭包的经典算法是弗洛伊德算法（Floyd-Warshall algorithm）[6]，其原理是动态规划：设路网图为D，其中，i点为发站、j点为到站，k为路网中的其他站点，Di,j,k为发站至到站且途径k中某个节点的最短路径的代价，i、j、k为1, 2, …, n。

（1）如果最短（最优）路径经过点k，则Di,j,k=Di,k,k-1+Dk,j,k-1。

（2）如果最短（最优）路径不经过点k，则Di,j,k=Di,j,k-1。

在实际运算中，算法成本需要考虑空间成本及时间成本，为节约空间，可以在原基础上通过迭代处理做降维操作，将空间降至为二维，如下所示：

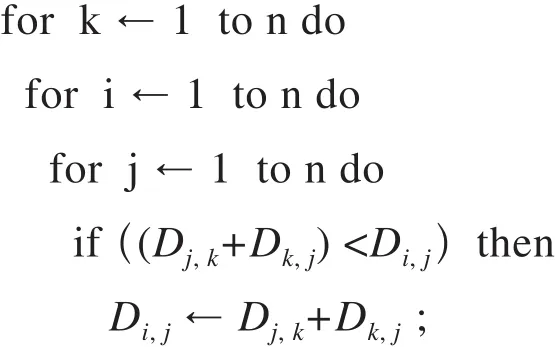
Di,j指发站i到达目的地j时的总代价，即车票、耗时、里程等综合代价值，当Di,j为∞，代表i、j两站点之间是不可到达的。

弗洛伊德算法的空间复杂度为O(N2)，时间复杂度为O(N3)。这个算法除了可以计算出传递闭包外，还可以算出每两个顶点间的最短路径。当然这个最短路径中的点到点的代价，可以是中转次数、里程、运行时间以及票价的加权值。由于该算法的时间复杂度较高，一个性能优化的做法是提前根据预设权值计算出经由传递闭包矩阵，那么实际应用中，需要查询时，时间消耗仅有O(1)。这个算法可以基本满足经由算法的要求，但是还具有局限性，比如，旅客希望自己选择中转次数，然后设定票价区间或中转时间差，那么这个算法需要重新计算点到点的代价，运行时间较长，而且仅能有一条最短路径的推荐，不符合旅客购票心理。

3 快速经由算法

快速经由算法需要解决如下旅客需求：

（1）接受旅客提出的中转次数的要求；

（2）在（1）的基础上，还需要接受旅客对换乘车次的里程，票价，中转时间差的要求。

3.1 中转次数

根据旅客提出的中转次数来选择铁路经由路线时，需要使用邻接矩阵的特性。

设路网图为G，具有N个乘车站的邻接矩阵A，使用二维数组N×N存放各乘车站之间关系数据，ai,j=1 表示i, j之间互通，否则 ai,j=0，表示i、j之间不可达。

也就是说，可以通过Ak来判断停靠站i到j是否存在中转次数为k-1的路线，如果存在，可以根据以下算法得到所有中转站：

function find Route Node(start Node, end Node, k){

if(k＜=1){

stack.push(#);//end of one route

return;

}

if(Ak== 1){

stack.push(end Node);

}

byte [] B = Astart Node,(1,…,n)k-1& A(1,…,n),end Node

for( index=0; index ＜=n; index++){

if(Bindex == 1){

find Route Node(start Node, index,k-1);

}

}

}

该算法的时间复杂度为O(Nk)，但前提是A2,…,Ak都已算好，Ak一次计算的时间复杂度为O(N3)。

3.2 附加需求

将旅客提出的里程、时间、票价等附加要求加入到查询条件中，需要通过邻接矩阵中附加信息来过滤。在构建邻接矩阵时，除了标注点到点的连通性外，还可以增加类似车次数据。

这些记录着车次信息的矩阵元素，均可为算法描述时间、费用提供依据。

4 优化及改进设计

快速经由算法可以通过程序具体实现方法来优化性能，改进用户体验。

4.1 数据预处理

数据提前处理生成，并在程序启动时就载入内存。这里的数据包括车次信息，停靠站信息，里程信息，票价信息等[7]。数据提前处理包括为停靠站编号，将列车相关信息组织成容易访问和获取的结构（其中，可以将全车次哈希成唯一数字ID，提升比较效率），通过将全车次数据排序预处理操作，提升后续计算的查询操作；根据停靠站信息构建经由邻接矩阵时，将站到站的直达列车信息附加到经由邻接矩阵元素结构中，在这过程中，可以根据预设的条件把一些列车过滤。

4.2 中转次数限定

提供合理的中转次数选择。快速经由算法在理论上支持旅客输入任意中转次数，但每个Ak的计算需要O(Nk)，比较合适的做法是假设一个中转次数的最高合理数k，然后提前生成A2, …, Ak，比如认为要求中转7次以上基本不可能，那么可以提前生成A2,…, A7。这样，可以很大程度上节省运算时间。

4.3 测试效果

将经由算法根据铁路的业务进行优化后，基于分布式内存数据库集群GemFire[8]的硬件环境下搭建了铁路旅程规划原型系统，并进行了实例测试。测试流程为模拟旅客输入基本的查询条件：乘车站、到站，乘车日期，算法根据旅客对时间、票价、换乘概率的要求对接续方案综合评分，高效计算出满足需求的接续方案。

测试样本数据包括既有的铁路路网数据、全国办理客运业务所有车站，及1 000个换乘站样本集，将火车站及开行车的样本数据初始化为路网图，如图1所示。

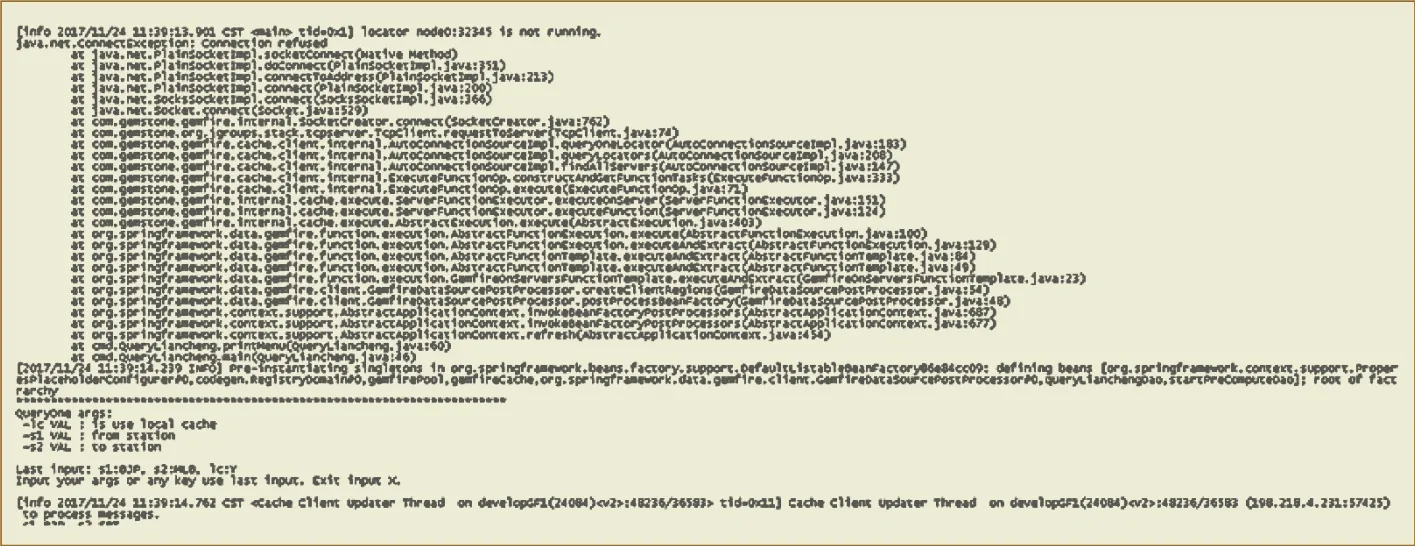
图 1 数据初始化

测试评价标准包括：换乘车站是否合理；接续方案是否可靠；综合评价是否易于接受。换乘方案的测试用例如表1所示。

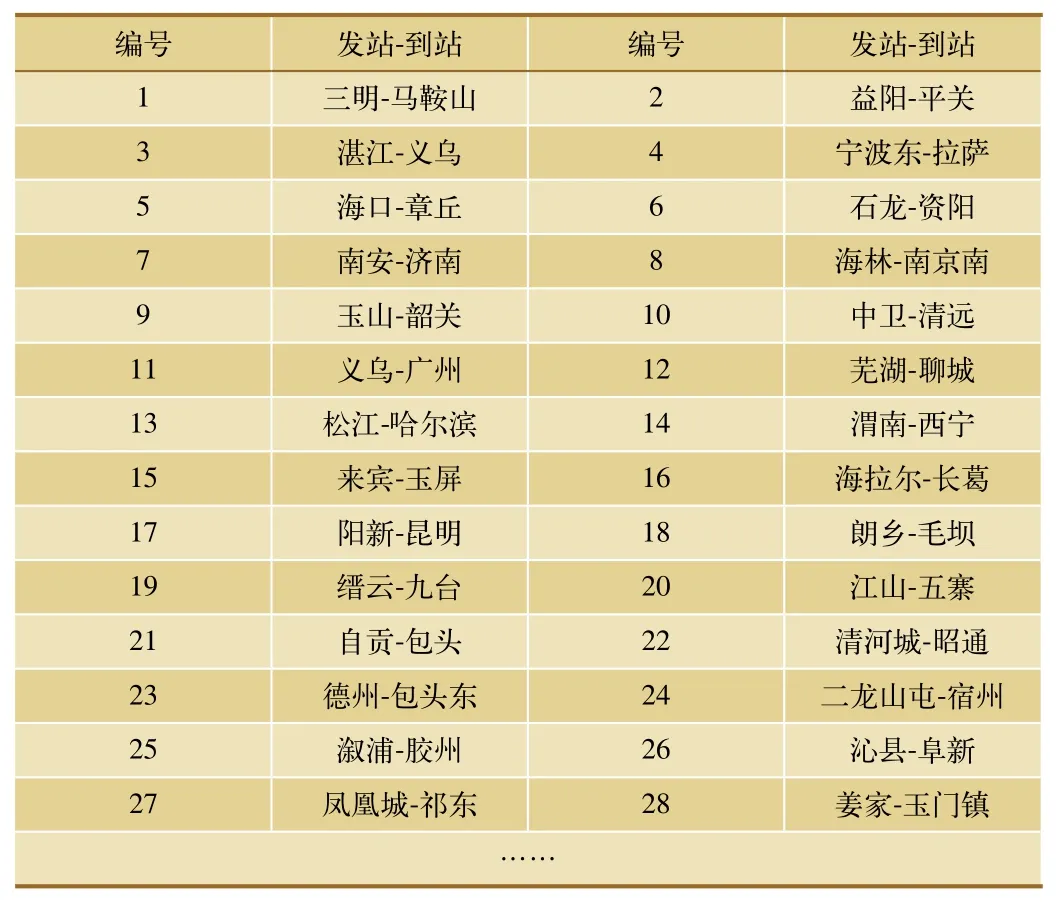
表1 换乘方案测试用例

如图2所示，出发城市为北京，到达城市为穆棱，两地之间经过算法计算获得9个建议的一次换乘城市的列表（其中，滨江与哈尔滨东、哈尔滨西为同城车站，长春与长春西为同城车站，高花与沈阳、沈阳北、沈阳南为同城车站等），与余票数据结合后，旅客获得联程产品如图3所示。

图2 简单展现一次换乘里程权重优先的方案图

测试过程中，设计了总体测试方案，每轮测试又设计了重点需要解决的方案，选择了具有代表性的城镇，涵盖了省会、大多数大中型城市、部分末梢车站、全部铁路枢纽车站。从测试结果看，测试方案涵盖面广，测试内容较为合理，对修正错误，调整、优化系统内容起到了较好的作用。测试结果表明，算法基于预处理数据方式，计算效率高效，换乘的方案比较合理、实用，初步达到了可以进行公测的条件。

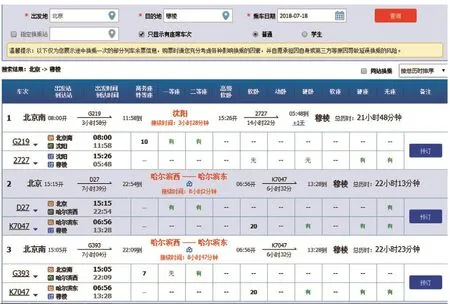
图3 一次换乘结果展示

5 结束语

铁路经由算法根据旅客的个性化需求，计算出的接续方案拥有不同的侧重点和灵活性。本文所研究的快速经由算法可以很好地解决根据旅客经由次数需求，以及附加的里程、票价、中转时间差要求的铁路经由问题。通过实际原型系统测试，该算法性能高效，运行平稳，证明了算法的正确性。