一种基于神经网络的硅基光伏组件运行温度在线软测量方法

于航，刘阳，连魏魏，朱红路

（1.龙源(北京)太阳能技术有限公司，北京市 西城区 100034；2.华北电力大学可再生能源学院，北京市 昌平区 102206）

0 引言

目前，光伏行业发展迅猛，2007—2017年全球光伏发电装机容量呈指数级增长。截至 2017年底，全球光伏发电的装机容量达到402 GW[1-2]。根据国际能源署的最高预测，到2030年全球太阳能光伏发电装机容量可能会超过1700 GW[3]。由于世界范围内光伏电站主要以硅基光伏组件为主，对于该类型的光伏电站而言，光伏组件运行温度是影响硅基光伏组件电气性能和效率的重要参数[4]。目前，硅基光伏组件运行温度建模受到了越来越多学者的关注。文献[5]探讨了硅基光伏组件运行温度受到的外部因素影响，如环境温度、风速以及太阳辐照强度等。针对诸多外部因素的影响，相关学者尝试建立它们之间的关联：硅基光伏组件运行温度和辐照量以及环境温度之间的联系[6]；硅基光伏组件运行温度系数与太阳辐照度和其他因素之间的联系[7]；组件运行温度函数，硅基光伏组件运行温度、外界环境温度等因素与光伏系统输出功率之间的联系[8]。以上研究表明，组件运行温度和外部环境因素之间具有很明显的关系。为了进一步研究组件运行温度与电气参数之间的关系，相关学者从光伏电站附近的地理和气候环境出发，研究了正确定位温度传感器位置处的空气流动性对组件运行温度的影响[9]；组件自身物理特性以及自身参数的影响、运行温度与短路电流、结电流的关系[10]；运行温度所引起的开路电压、填充因子的下降，进而带来组件的效率下降等等[11]。由于运行温度对硅基光伏组件的效率和性能有着重要影响，许多学者对硅基光伏组件的运行温度计算问题进行了探索[12-14]。由于每个电站的地理位置，环境差异较大，且不同组件自身材料特性和安装环境也各不相同，因此想要建立精确的机制模型十分困难。文献[15]采用理论模型对硅基光伏组件运行温度进行计算，然而其计算结果与实际状况仍存在一定的误差。文献[16]针对组件运行温度的计算建立了太阳辐照度和硅基光伏组件运行温度的线性相关分析模型，但是模型参数的获取较为复杂，一般光伏组件厂商提供或者实验测试。文献[17]提出Hottel-Whillier-Bliss (HWB)公式来对硅基光伏组件运行温度进行修正计算，但是受到条件限制，缺乏良好的泛化性能，难以直接工程应用。

综上所述，在复杂和恶劣的工作条件下，光伏组件的运行温度受到实际环境中各种因素的影响，电站地理位置信息，电站自身性能的衰退，使得采用机制模型算法较为困难。但最重要的是，机制模型在建模时，由于所涉及的建模环节、模型参数众多，且受建站成本的限制，在现场实际运行条件下机制模型要得到所有输入变量以及模型参数是不可能的[18]。针对上述问题，本文提出一种基于多层反向传播(back propagation，BP)神经网络的硅基光伏组件运行温度计算方法。由于光伏电站的历史运行数据不仅包含了电站自身位置、结构等信息、外部环境状况(太阳辐照度、环境温度、湿度、风速)，而且能够体现组件自身特性(效率降低等)，因此所提基于多层BP神经网络的组件运行温度计算模型，采用电站历史运行数据不仅可以避免物理模型的复杂分析过程，以及模型参数难以获取等问题，而且相比于单层隐含层 BP神经网络模型，其泛化能力更强，计算简单、高效、性能较好，可以有效地应用于相关工程计算中。

1 运行温度对光伏组件效率的影响

当光伏组件运行温度发生变化时，短路电流ISC和开路电压USC分别为：

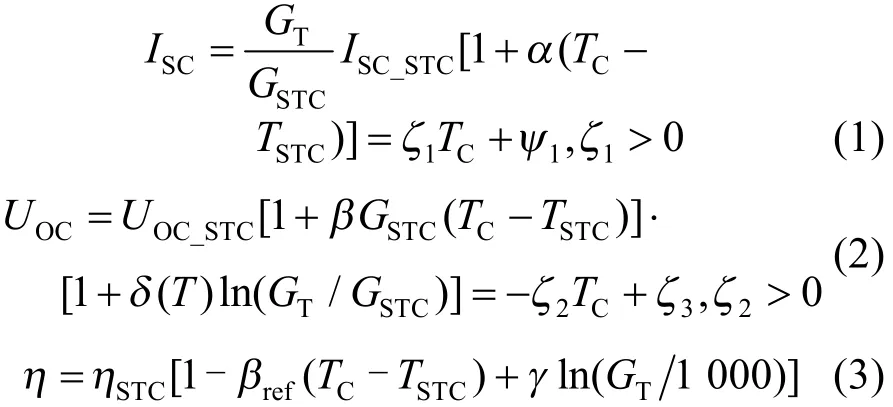
式中：GT为硅基光伏电池工作时的光照强度，W/m2；GSTC为标准测试条件下的光照强度，W/m2，GSTC为 1 000 W/m2；TC为组件运行温度，℃；TSTC为标准测试条件下的电池温度，℃，TSTC为 25 ℃；α为短路电流温度系数，α通常由生产厂家提供；ISC_STC为标准测试条件下的硅基光伏电池短路电流；UOC_STC为标准测试条件下的硅基光伏电池开路电压；β为开路电压温度系数；δ为太阳辐射强度的校正因子；为只考虑组件运行温度是相应电气参数的系数，其中≪；ηSTC为硅基光伏电池在标准测试条件下的发电效率；γ为辐照度系数；βref为参考状态下的温度系数 ，K-1。

式(1)和式(2)说明了短路电流和开路电压在辐照度一定的条件下与组件运行温度之间的关系。从式(1)和式(2)可知：短路电流随着组件运行温度有微小的增大；开路电压则随着运行温度的增大明显减小。由于≪，因此，随温度增高，硅基光伏电池的开路电压显著变小，短路电流微小变大，最终导致其效率随着温度升高而降低，如图1所示，具体数值关系可以由式(3)进行描述。式(1)—(3)描述了硅基光伏电池的相关电气特性及其电气参数受外部环境影响的变化规律，分析了组件运行温度通过影响短路电流和开路电压，从而影响组件转化效率的过程。各个公式中的参数和相关变量多由组件生产厂家给定或需要现场测试得到，且这些参数并不是固定不变的，光伏组件可能受到恶劣环境条件的影响导致性能退化、厂家生产工艺的差异、实际现场状况以及施工条件的不同等因素的影响，导致相关参数畸变，同时由于光伏电站相关数据采集设备未有效及时配置，使得所需实际参数无法直接获取，只能通过间接的方法得到，最终导致计算结果和实际值之间偏差较大。

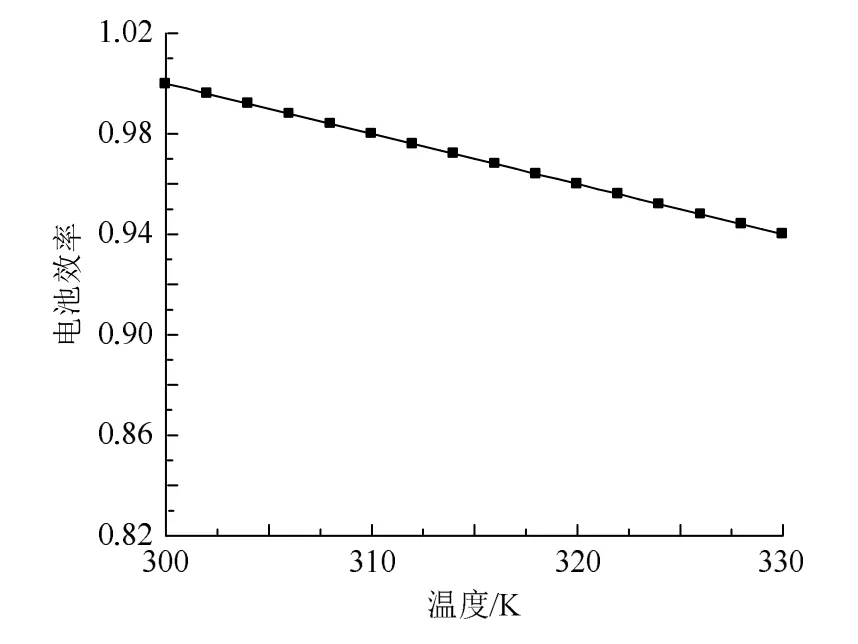
图1 硅基光伏电池的效率与温度的关系Fig. 1 Relationship between efficiency and temperature of silicon-based PV cells

2 硅基光伏组件运行温度的计算及实证分析

2.1 硅基光伏组件运行温度计算模型

从第1节分析可知：短路电流随着组件运行温度有较为微小的增大；开路电压则随着运行温度的增大明显减小；光电转化效率随着温度升高而降低。从光伏电池机制层面探究其原因主要是由于组件运行温度提高，热激发态电子在半导体的电气特性中开始占据主导地位，并且填充因子大幅度减小。在工程应用上，考虑硅基光伏组件运行温度的光伏系统输出功率PTc_r为

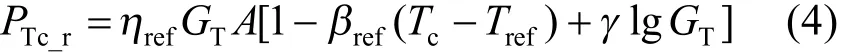
式中：βref为硅基光伏组件的温度系数，对于硅基光伏组件，一般取0.004 K-1；Tc为硅基光伏组件运行温度，简单起见γ的值通常可以设为0。相比于直接利用环境温度来进行光伏输出功率的计算方法 P =ηrefGTA而言，此种方法考虑到了组件运行温度对于光伏电站输出功率的影响，发电量计算结果有一定的提高。但是对于容量几十MW的光伏电站，组件数量众多，且空间覆盖面积广阔，为每一个组件或每一串组件安装温度采集器不现实，不仅成本剧增，而且信息维护困难。因此在实际环境条件下大型光伏电站组件运行温度是难以获取的。

光伏发电机制建模主要是依据太阳辐照度传递过程、光伏组件光电转化方程、相关设备运行方程、详细的地理位置信息等，建模环节众多，模型结构复杂，参数求解困难。因此，对于大多数的机制模型来说很难应用于光伏组件在线温度的计算。在实际应用中，较为常用的光伏组件运行温度计算如式(5)所示，该公式建立了组件运行温度和环境温度之间的关系：

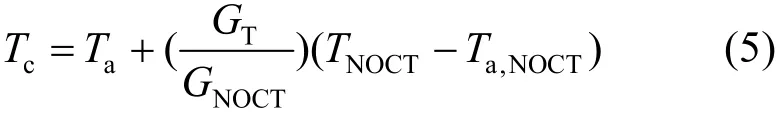
式中：Ta为环境温度；TNOCT为硅基光伏电池标称工作温度，是指当硅基光伏组件或硅基光伏电池处于开路状态，并在一定条件下(硅基光伏电池表面光强强度为800 W/m2，环境温度为20℃，风速为1 m/s，支架结构为后背面打开)所达到的温度。

2.2 实证平台的描述

为评价上述光伏组件运行温度计算方法的性能，搭建了光伏发电实证测试平台进行测试。图2说明了实证测试实验平台的系统构成方式以及温度传感器布置方式，图3给出了实验平台气象数据采集以及温度测量设备，可以采集外部环境参数以及组件运行温度等数据，每块组件按照图 2布置方式设置 5个温度传感器，型号为PT100，文中的分析过程取各温度测点的平均值。

2.3 实证分析

为说明上述经验公式方法的性能，将实证测试平台的实测倾斜面太阳辐照度和环境温度作为输入，基于经验公式(5)可以计算出相应的组件运行温度。由于光伏组件运行温度在不同季节条件下存在较大的差异，因此针对各典型季节分别展开了计算分析，相应的组件运行温度计算结果如图4所示。从图4可以看出，实际组件运行温度明显高于环境温度，而由经验公式(5)所得到的运行温度计算值则介于二者之间；且组件运行温度随季节状况变化明显。

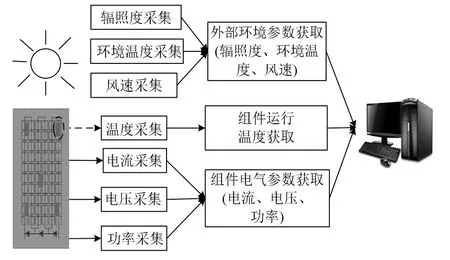
图2 实证测试系统结构示意图Fig. 2 Structure schematic diagram of experimental test system

图3 实证平台气象数据采集及温度测量设备Fig. 3 Meteorological data acquisition and temperature measurement equipment of empirical platform

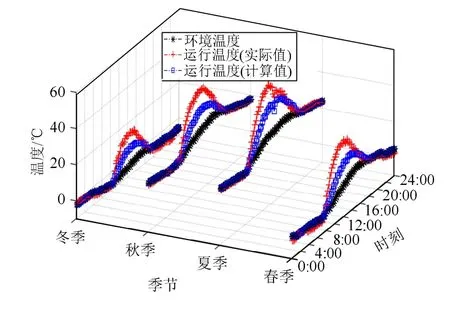
图4 典型季节条件下硅基光伏组件运行温度计算分析Fig. 4 Calculation and analysis for operating temperature of silicon-based PV modules under typical seasonal condition

以上分析仅为定性的结果，为量化评价光伏组件运行温度计算模型的性能，本文分别选择最大误差εMaxError、标准差εSTD、均方根误差εRMSE、平均绝对误差εMAE等指标对组件运行温度计算结果进行评价，相应指标计算公式为：

式中：Tc_r,i为电站实际运行状况下组件运行温度；Tc_C,i为经验公式(5)下的组件运行温度计算值；Tc_mean为组件运行温度计算值的算数平均值；n为样本数量。同理，引入环境温度和光伏组件运行温度之间的误差用于经验计算的对比分析。量化的分析结果见表1。

通过图4和表1可以得到如下结论：组件运行温度受到季节状况的影响，不同季节条件下组件运行温度差距较大；环境温度和组件实际运行温度之间差距较大，在进行发电量的计算中组件运行温度和环境温度之间不具有互换性，仅以环境温度代替组件运行温度得到的发电量结果偏差较为明显；经验公式计算得到的组件运行温度相比于环境温度来说更加接近于组件运行温度，但是其仅仅能够描述组件运行温度的变化趋势，存在较大误差；同时，面对复杂的外部环境状况以及随着电站服役时间越久，光伏系统自身性能退化越来越严重，其发电量和辐照量、组件运行温度的关系并不是一成不变的。因此，随着时间和运行状况的改变，利用经验公式来实现光伏组件运行温度的精确计算是不可行的，需要找到一种具有自学习能力，可以面对以上复杂的状况，同时计算精度高的方法。

表1 在典型季节条件下硅基光伏组件运行温度的计算误差分析Tab. 1 Error analysis about calculation for the operating temperature of silicon-based PV modules in typical seasons ℃

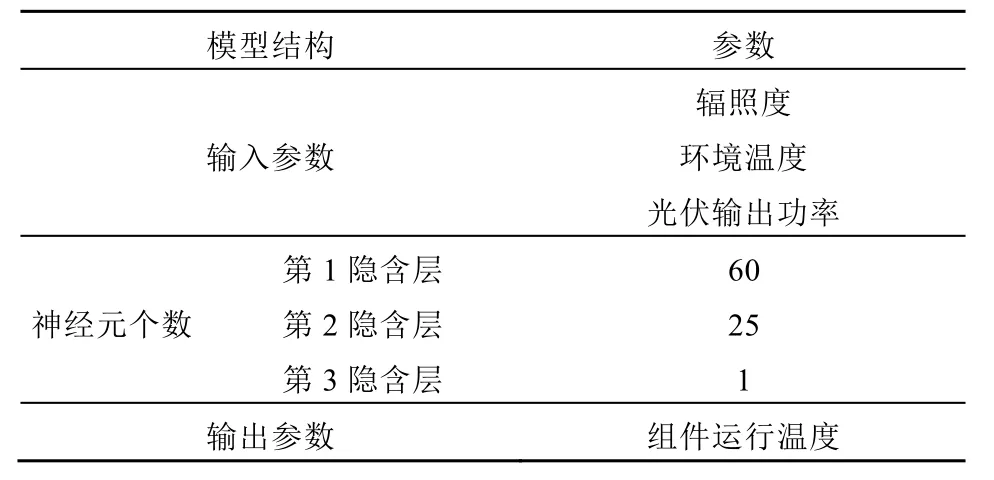
表2 多层BP神经网络模型参数配置列表Tab. 2 Parameters configuration list of multi-layer BP-ANN model

图5 光伏组件运行温度计算多层BP-神经网络模型Fig. 5 Multi-layer BP-ANN model for operating temperature calculation of PV module

3 基于多层BP神经网络的硅基光伏组件运行温度计算方法

BP神经网络是使用最为普遍的神经网络算法，能够学习和存储大量的输入-输出之间的映射关系，它的最终目标则是通过反向传播误差不断调整网络的权值和阈值，使得误差的平方和最小[19]。由第2节分析可知，由于机制建模所涉及的建模环节众多，模型结构复杂，参数求解困难，并且各个环节所涉及的模型变量和参数不易获得，因此，很难应用于光伏组件在线温度的计算。针对BP神经网络，多层结构的网络相比单层的结构泛化能力更强，拟合非线性的能力增加，误差更小[20-21]。因此本文采用多层BP神经网络方法来建立光伏组件运行温度的计算模型，构建一个 5层 BP神经网络模型，选择太阳辐照强度，环境温度、光伏系统输出功率作为5层BP神经网络模型输入变量，同时选择硅基光伏组件运行温度作为多层BP神经网络模型的输出变量。

由于风速的大小与组件散热有关，会影响光伏组件的运行温度，在这里将风速作为一种可选择的模型输入变量。基于多层 BP神经网络的硅基光伏组件运行温度模型参数配置见表2。

按照表2模型参数配置表来建立多层BP神经网络的光伏组件运行温度计算模型，如图5所示。通常情况下，神经网络的应用主要包括3个步骤：采集训练样本、训练网络结构、测试网络。本文设计的光伏组件运行温度在线软测量方法采用的是离线训练神经网络，利用训练好的模型在线计算组件运行温度。即根据实验平台大量样本数据，在Matlab平台上训练神经网络，得到最佳的网络权值、阈值以及训练函数等其他参数，最后基于神经网络模型实现光伏组件运行温度的在线软测量。

所设计的 5层神经网络隐含层函数依次为tansig函数，tansig函数以及purelin函数；输出层函数采用traingd函数；训练次数设置为5 000次，训练精度设置为 0.001。按照以上参数训练神经网络得到所需的各连接权值和阈值，依据训练好的神经网络结构就可以编写程序，实现组件运行温度的在线计算，相应的在线计算流程如图6所示。

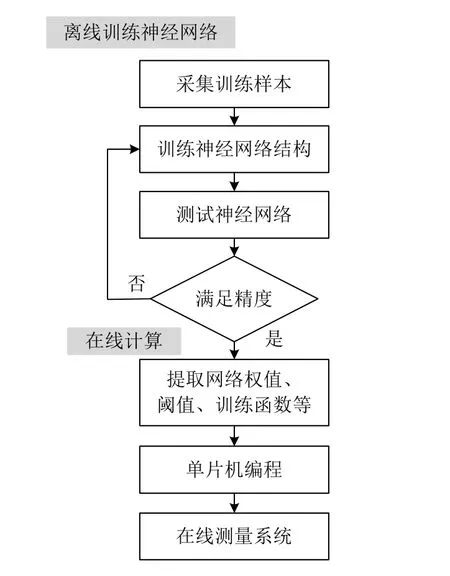
图6 光伏组件运行温度在线计算流程图Fig. 6 Flow chart for operating temperature online calculation of PV module

4 结果和讨论

由于 BP神经网络的训练依赖样本数据的大小，为了明确训练数据集大小对于所提模型精度的影响，选取不同数据集大小的样本数据进行训练，见表3。将光伏实证平台2016年全年的历史运行数据按照不同时间尺度样本数据(7天、15天、1月、3月、6月、1年)各分成6组进行统计分析，其中80%的数据用于训练，剩余20%的数据用于测试。

利用表2参数来建立基于多层BP神经网络的硅基光伏组件运行温度计算模型。为了探究风速对于光伏组件运行温度的建模是否存在影响，实验设计中将所建立模型分为2组来对比分析风速的影响。

由表3可知：

1）所提多层BP神经网络模型的计算误差随着训练样本的增大而逐渐减小；相反，模型的训练时间随着样本的增大而逐渐增加，有明显的变化趋势。

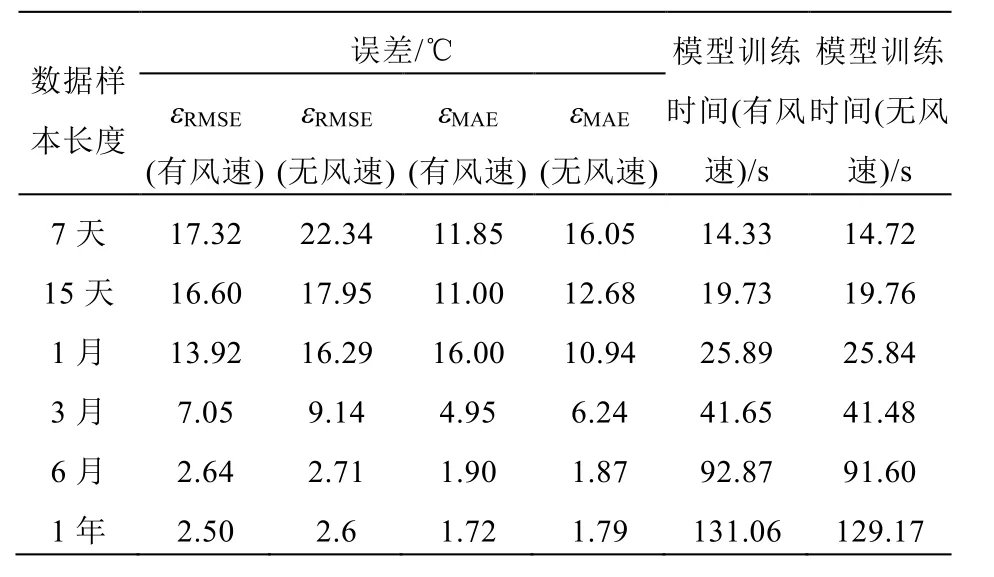
表3 多层BP-神经网络建模结果(有/无风速)Tab. 3 Modeling results of multi-layer BP-ANN(w/or w/o wind speed)

2）风速对于提高组件运行温度模型的计算精度是有帮助的，因此，在条件允许的情况下，组件运行温度的模型计算中应考虑风速的影响。

因此，为了保证模型的精度要求，本文选择一年的样本数据用于模型的训练，同时神经网络模型采用离线的方式训练得到。表3和表4分别统计了不同样本大小条件下模型训练时间和不同天测试数据的在线计算时间，论文方法在线计算时间耗时在ms级别，满足实时在线计算的要求。

为了验证所提多层BP神经网络运行温度模型的准确性和普遍适应性，以及是否满足在线计算的时间要求，选择2016年9月30日—2016年10月3日连续4天实测电站运行数据，对光伏组件运行温度的在线计算结果进行分析。从计算时间来看，本文所提方法在线计算的时间耗时在ms级别，满足实时在线计算的要求。图7展示了所提多层BP神经网络运行温度模型和前述经验公式(5)的建模结果。误差的计算结果如表4和图8所示。可以看出，经验公式所得结果具有较大的误差，本文所提的基于多层BP神经网络的组件温度计算方法具有较好的性能，精度较高。

5 结论

在实际应用中采用机制模型进行光伏组件温度的计算不仅相关模型参数难以获取，计算过程复杂，而且具有较大的误差。同时为了寻求更加有效、计算简单、且泛化能力强的方法来计算组件运行温度。因此，在神经网络的基础上，本文提出了基于多层 BP神经网络组件运行温度的计算方法。通过本论文分析能够得到如下结论：

1）基于多层BP神经网络的组件运行温度计算方法对非线性对象具有较强自学习能力，模型泛化能力较强，且历史训练数据中已经包括了光伏电站自身特征的历史信息，能够适应电站的动态变化特性；

2）本文提出光伏组件运行温度计算方法能够利用现有可测量参数，实现光伏组件运行温度的在线软测量，进而代替温度传感器测量；

3）针对大型光伏电站，本文所提方法能够在线监控各部分组件的运行温度情况，从而可以得到更加精确的发电量计算结果。

4）采用经验公式计算得到的组件运行温度误差较大，对比于机制模型复杂的计算过程，本文所提方法简单高效，且具有更高的计算精度，同时本文方法计算耗时满足在线计算的要求，可以应用于实际工程。

表4 误差分析Tab. 4 Error analysis

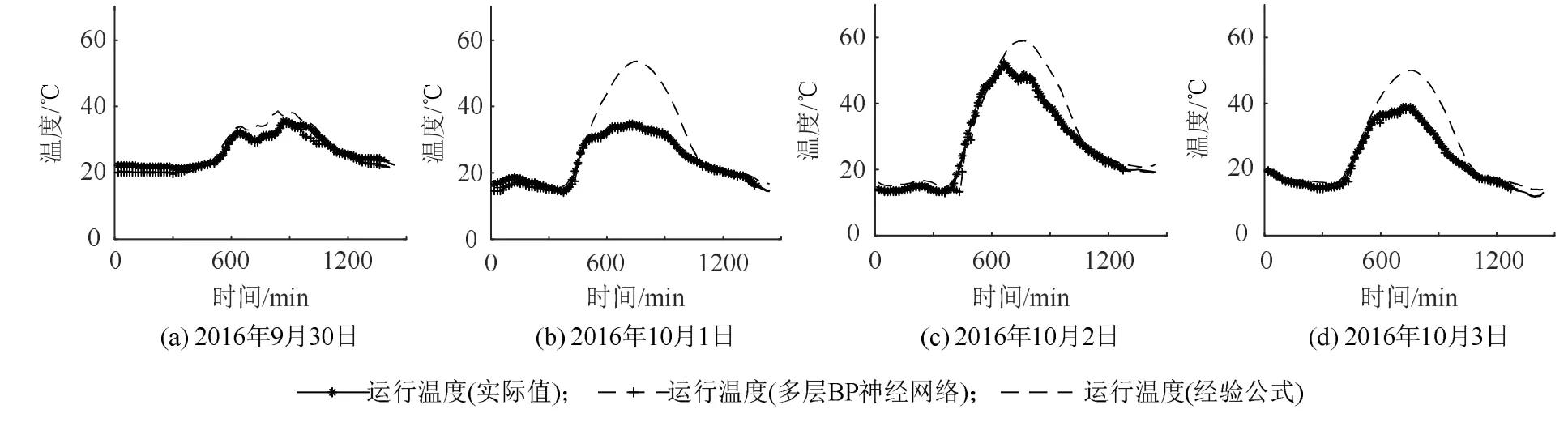
图7 硅基光伏组件运行温度计算结果Fig. 7 Calculation results of operating temperature of silicon-based PV modules

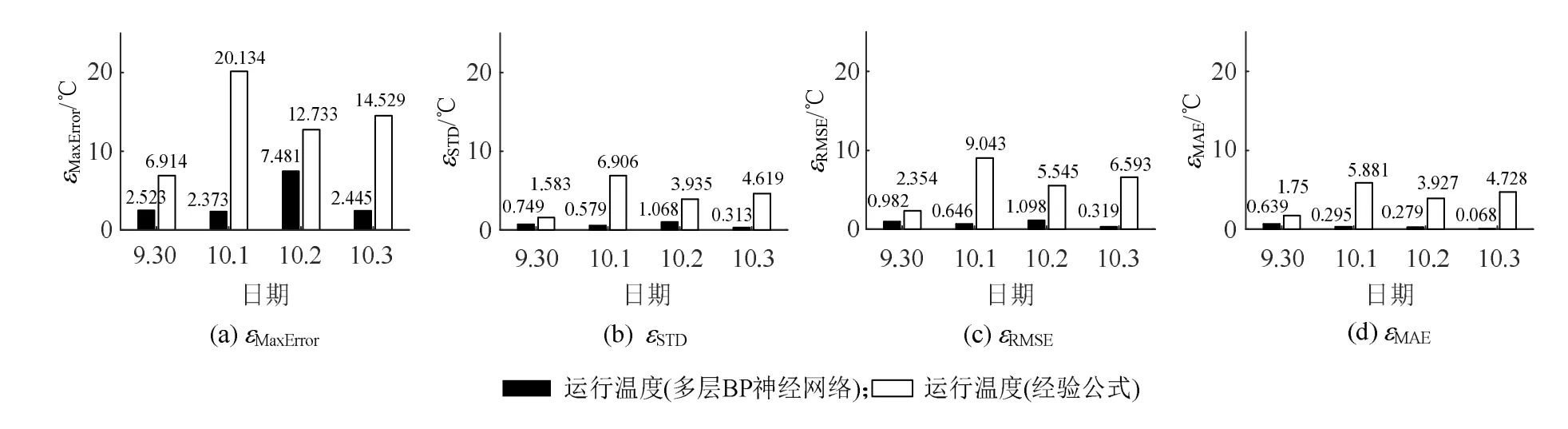
图8 硅基光伏组件运行温度误差分析Fig. 8 Error analysis of silicon-based PV module operating temperature