基于随机线采样的磁共振图像重构算法研究
吴章洪
(成都大学 美术与设计学院, 四川 成都 610106)
0 引 言
磁共振图像是一种基础医疗诊断工具,压缩感知(Compressed sensing,CS)为磁共振图像中的应用提供了潜在的减少扫描时间的可能[1].磁共振图像若要成功应用CS必须满足2个关键要求:医疗影像是可压缩的或是稀疏的;磁共振图像扫描仪获得的是编码后的样品,而不是直接像素的样本[2].磁共振图像获得的编码样品通过求解凸优化问题找到信号的逼近.目前,科研人员提出了许多凸优化方法,例如内点法、梯度投影方法和迭代阈值法等[3].本研究针对阈值迭代法无法区分稀疏系数尺度位置并且存在着恒定偏差的问题,提出了一种新的阈值函数与数据约束一致性的方法重构磁共振图像.
1 理论基础
1.1 相关性
CS中若要完全恢复图像,稀疏矩阵与采样矩阵必须满足RIP性质,而直接测量RIP性质非常困难,本实验通过计算采样矩阵Φ和稀疏基Ψ之间的相干性来探测.采样矩阵Φ和稀疏基Ψ之间的相干系数定义为,
(1)

1.2 图像重构理论
CS在磁共振图像中的应用可以描述为:假设有一幅磁共振图像x,此图像在小波变换域或者奇异值分解下是稀疏的,稀疏基为Ψ,采样矩阵为Φ,图像的测量值为y,其中y=φ×φ×x.若对磁共振图像进行恢复,其重构算法[5]可以描述为,
(2)
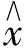
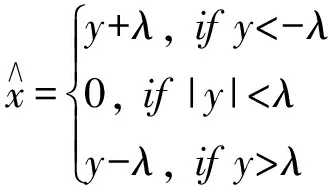
(3)
由式(3)可知,其解的形式与软阈值函数相似,阈值迭代算法的实现是根据软阈值函数求解以及约束数据的一致性进行图像的恢复,其具体实现步骤如下:

其次,根据约束数据一致性理论,
(4)
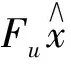
(5)
磁共振图像通过欠采样方式获得观测值.根据采样理论,对复杂信号进行采样时,如果采样时钟频率不到信号中最大频率的2倍,则会出现一种称为“混叠”的现象.若把“混叠”现象看成是噪声,则对磁共振图像的恢复可看成是“去噪”的过程,可采用式(3)的方法恢复图像.但式(5)有2个变量,因此没有具体的解的形式.式(5)常用的解决方案是软阈值函数和数据约束一致性相结合来恢复图像,但是由于软阈值函数对于原系数和小波分解系数存在恒定偏差,由式(3)可知,软阈值函数估算信号时,只是简单地加减λ,因此函数无法区分稀疏系数尺度的位置,所以尽管整体上重构信号在欧氏距离上逼近原信号,但是存在低尺度能量搬移到高尺度的现象,从而容易出现不期望的人工效应.当软阈值函数在|y|<λ时,其估算值全部置0,会产生截断效应,导致许多细节信息丢失,影响图像重构精度.对此,本研究采用新的阈值函数和约束数据一致性的方法恢复图像.新的阈值函数为,
(6)
式中,k=log2(|λ/y|∧n+1),相当于一个调节因子.当|y>λ|,0 为验证本研究提出的算法恢复磁共振图像的效果,采用MATLAB软件进行仿真实验. 研究对象为256×256的大脑磁共振图像,如图1所示. 图1大脑磁共振图像 采用小波变换基作为稀疏基,随机线矩阵为采样矩阵,采样线的条数是60,如图2与图3所示. 图2小波变换稀疏后的图 图3采样矩阵 软阈值函数与新阈值函数恢复图像后的效果如图4所示. 图4 函数重构图 根据仿真实验的结果,本研究从图像恢复的信噪比、图像在不同稀疏基下重构的时间及相干性3个方面作为评价图像恢复的标准.实验结果如图5、表1~表3所示. 图5 2种采样矩阵图像恢复的信噪比 表2 不同稀疏基作用下2种函数对应图像恢复的时间比 表3 矩阵之间相关性的对比 根据CS理论可知,图像恢复的信噪比越高,均方误差越小,图像恢复的质量就越高. 仿真实验结果表明,新阈值迭代算法能有效地解决原阈值迭代法无法区分稀疏系数尺度的位置和存在着恒定偏差的问题,同时能精确地重构图像,达到了本研究期望的结果.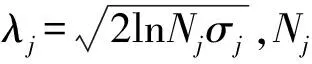
2 仿真实验
2.1 实验软件
2.2 实验对象

2.3 参数设置


2.4 实验结果

2.5 数据分析




3 结 语

