亚音速壁板弱非线性动力学模型响应预测

黎昭文， 李 鹏， 杨翊仁

(西南交通大学 力学与工程学院， 四川 成都 610031)

0 引 言

研究表明，高速列车在运行时， 其车身蒙皮等壁板结构与流体之间存在强耦合作用会出现严重的气动弹性问题[1].事实上， 气动弹性力学系统的研究需要同时关注结构与气动力两者之间的耦合作用.针对该问题， 科研人员做了大量研究[2-8].研究表明，对高速列车运行这类低马赫数流动问题， 其车身壁板上的气动力可用线性模型表征，在考虑壁板结构非线性环节后的气动弹性动力学模型可用一类典型的非线性VanderPol-Duffing方程来表征.故， 本研究拟基于Volterra级数采用脉冲响应法对模型系统进行辨识， 并对该模型系统的动力学响应进行预测， 从而建立该类气动弹性问题的响应分析方法.

1 Volterra级数理论

研究发现，Volterra级数适用于时不变弱非线性系统的建模，其可在任意精度上逼进集上的连续函数[9].任意时不变的离散系统对任意输入u[n]的响应y[n]可用无限项的多维卷积分描述，

k1,n-k2]u[k1]u[k2]+…+

n-km]u[k1]u[k2]…u[km]+…

(1)

式中，n=0,1,2,…，是离散时间变量，h0是定常状态响应，hm[n-k1,n-k2，…，n-km]是系统的m阶核.若能识别出系统的各阶核，则系统对于任意输入的响应都可以通过上述卷积求得.

各阶核的识别过程是Volterra级数模型建立的关键步骤.研究显示，核识别的方法包括脉冲响应法、阶跃响应法和准阶跃响应法等[10].本研究拟采用脉冲响应法识别模型系统的各阶核.

设该模型系统的定常状态h0=0，则式(1)可写为如下的二阶截断形式，

k1,n-k2]u[k1]u[k2]

(2)

定义离散时间域内一维单位脉冲、二维单位脉冲为，

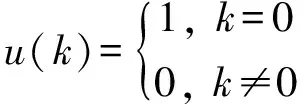
(3)

u(τ1)=u(τ1-k1)+u(τ1-k2)， 0≤k1≤k2

(4)

按识别要求分别施加脉冲信号于式(2)，可得其一阶核的表达式为，

(5)

式中，当y0[n]为零时施加信号(1)的响应，y2[n]为零时施加双倍幅值信号(1)的响应.

模型系统的二阶核的表达式为，

h2[n-k1,n-k2]

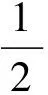
(6)

式中，y1[n-k1,n-k2]为施加信号(4)的响应，y0[n-k1]和y1[n-k2]分别为在k1和k2时刻施加信号(3)的响应.

一阶核h1[n]为时间n的一维函数，表示非线性系统的线性子系统特性，也可表征一定的非线性特性，且比非线性系统纯线化后的线性核更加合理.二阶核是关于时间n和时移k1-k2的二维函数序列.

2 壁板模型的动力学系统与响应预测

2.1 壁板模型的动力学系统与方程

两端简支的黏弹性二维壁板模型如图1所示.壁板上表面有沿轴向的不可压缩亚音速气流，气流密度及速度分别为ρ∞与U∞，壁板上表面作用有扰动气流及基座扰动所致简谐激励力.

图1二维壁板模型

描述该模型的气动弹性系统的无量纲动力学方程[1]为，

(7)

式中，质量m=ms+mf、刚度系数k=ks+kf，其中下标s表示结构相关项，f表示与流体相关的附加项，其随流体的密度与速度的改变而变化；阻尼系数μ和非线性项系数k3只与结构参数相关；外激励幅值F0和外激励频率ω均与扰动气动力和基座激扰有关[11].

式(7)所表征的方程可视为弱非线性系统，可用其对模型的动力学系统响应进行预测.

2.2 非线性响应预测

首先，将式(7)右端项替换为脉冲激励P，并将式(7)降阶为一阶微分方程组，

(8)

表1 计算参数

基于表1的参数，图2(a)给出模型系统起步阶段的响应的数值计算及理论预测解，图2(b)～(d)给出了模型系统稳态阶段的数值计算及预测解.

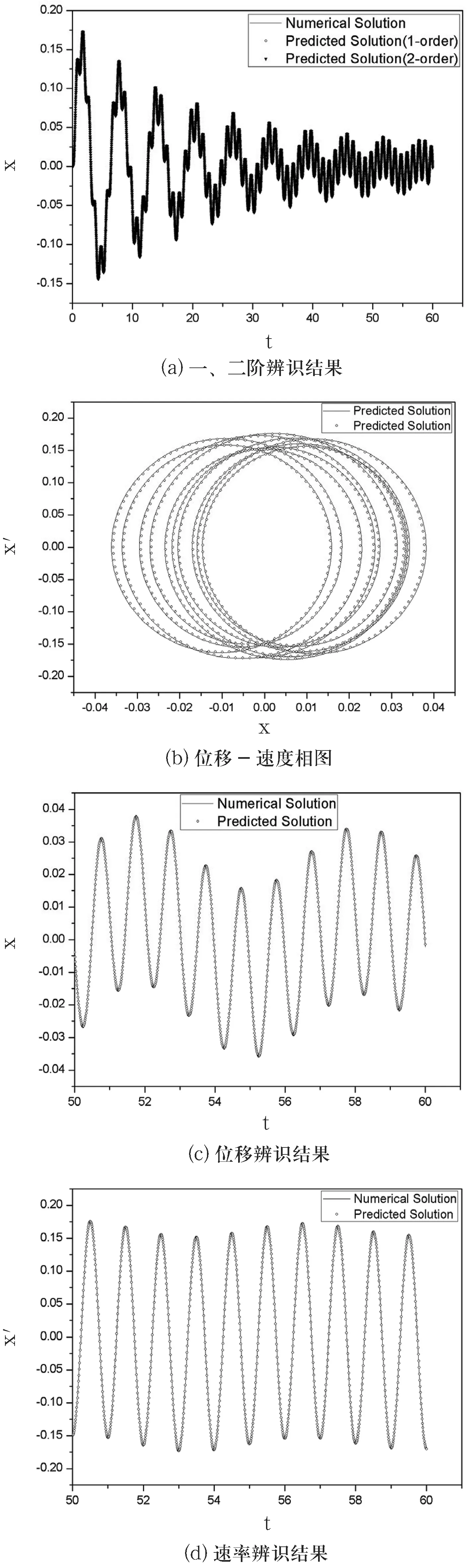
图2 模型系统的动力学响应预测结果

由图2(a)可知，采用一阶核可较好地预测该模型的响应，且对其起步阶段及稳定阶段的响应均有很好的预测.因二阶核对一阶核的修正效果有限，故本分析中仅使用一阶核进行系统的响应预测.

为研究模型系统的参数对响应预测的影响，需要对方程(7)中的可变参数进行分析以确定其合理的变化范围，从而保证获得较好的识别效果.

2.2.1 流场参数.

流场参数可由质量m和刚度系数k表征.计算发现，随着m值的变大，其响应的预测效果将会逐渐变差，结果如图3所示.从图3可知，系统的响应预测值在峰值处已经出现了明显的差别.同时，由计算可知，当k相对较大时，系统响应识别效果较好，结果如图4所示.从图4可知，当k逐渐变小并趋于零时，系统的响应预测效果会显著变差.这主要是由于系统处于零刚度的失稳临界状态.故，相对较小的m和相对较大的k能够保证模型系统有较好的预测效果.

图3m=2时位移预测结果

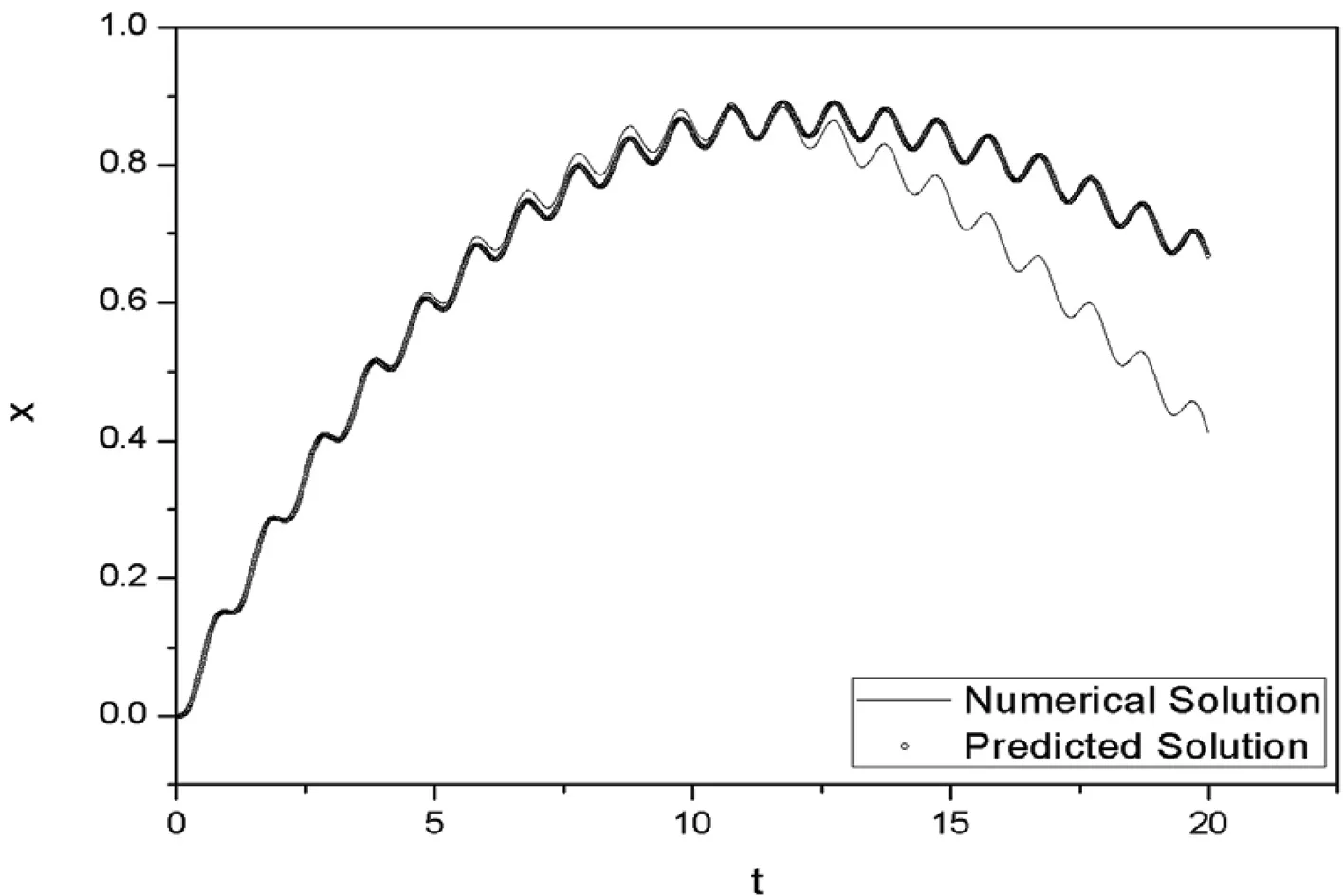
图4k=0.01时位移预测结果

2.2.2 结构参数.

结构参数主要由阻尼系数μ和非线性项系数k3表征.计算发现，预测效果对μ值变化并不敏感，但会影响系统趋于稳态的时间，即μ越大其进入稳态的时间就越快，图5给出了μ=1时的系统响应预测结果，进入稳态时间与μ=0.1相比明显变短.同时，由计算可知，随着k3的增大预测效果会变差，图6给出了k3=10时系统起始段预测结果.由图6可知，为保证模型系统有较好的预测效果，应使k3相对较小.

图5μ=1时位移预测结果

图6k3=10时位移预测结果

2.2.3 激励参数.

激励参数主要由外激励幅值F0和外激励频率ω表征.计算发现，F0的大小对模型预测结果的影响不明显，但对系统的位移幅值的影响较大，结果如图7所示.同时，由计算可知，ω值越小，预测效果越差，结果如图8所示.据此可知，相对较大ω值可保证模型系统有较好的预测效果.

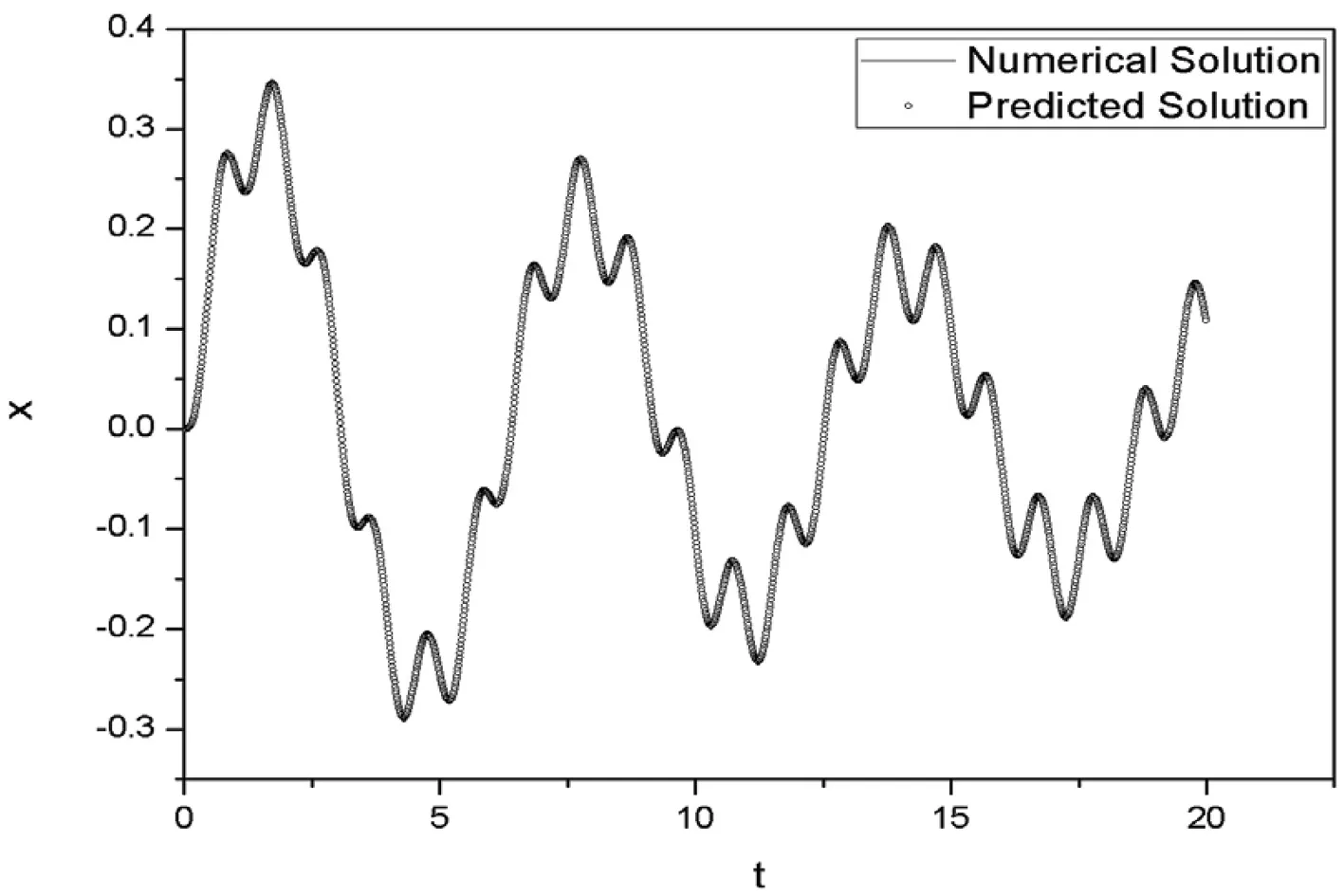
图7F0=2时位移预测结果

图8 ω=0.1 π位移预测结果

3 结 论

本研究选取表征亚音速壁板非线性动力学模型系统的VanDerPol-Duffing方程，并对其进行了研究，基于Volterra级数对模型进行核识别并建立相应的系统以进行动力学响应预测.研究表明：对该类弱非线性问题，基于一阶核所构建的Volterra模型对系统的响应有较好的预测效果；系统的阻尼系数μ和外激励幅值F0对预测精度无明显影响，系统的质量m和非线性项系数k3的值相对越大，则预测精度越差，刚度系数k和外激励频率ω的值相对越小，其预测精度越差.