时间约束下任务关键系统的可调度性分析
陈 莹,邢建春,杨启亮,,张孝鹏
(1.陆军工程大学 国防工程学院,南京 210007; 2.南京大学 计算机软件新技术国家重点实验室,南京 210093;3.酒泉卫星发射中心,甘肃 酒泉 732750)
0 概述
任务关键系统(Mission Critical System,MCS)[1]是指在系统运行过程中不能发生中断或失效,否则将导致任务执行失败,造成严重的经济损失或人员伤亡的系统。如何在时间有限的情况下保证现有的关键任务持续、及时完成,己成为亟待解决的问题。时间约束下的任务关键系统的可运行性分析,也就是确保有限时间约束内能够完成任务的触发问题。因此,首先需要研究整个系统中所有活动是否都为可调度的。
在工作流网系统中,如果任何2个变迁之间都不存在潜在的资源冲突,那么称此工作流模型是可调度的。对于不可调度的活动,结合关键任务等级,通过对活动的时间约束进行修正使得工作流模型变成可调度[2]。时间约束下的任务关键系统的调度性问题本质上是一个非线性规划问题[3]。
时间约束下工作流程的建模是其时间性能分析的前提,具有强大时间约束表达能力和数学基础的时间约束Petri网(Timing Constraint Petri Net,TCPN)在建模方面得到了广泛应用。然而,TCPN强大的时间约束描述能力也使得可调度性的分析难度大大增加。因此,众多学者从不同角度对其进行了研究。文献[1]提出了TCPN的概念,并给出了最基础的调度验证的方法,很多学者的研究都基于此方法;文献[2]提出了基于Petri网的时间约束工作流的可调度性验证算法;文献[4]从结构、时间、资源限制3个层面提出多工作流系统的原型,并进一步给出多工作流网下的可调度性验证算法和修正策略;文献[5]完善了TCPN的定义,并提出了TCPN时间可调度性判定定理;文献[6]提出了4种基本工作流组件模型的简化规则和压缩推理方法;文献[7]对文献[2]的验证算法进行了改进,使得算法更加简洁,减小了时间复杂度;文献[8]提出了扩展的时间约束Petri网(w-TCPN)的定义,并结合w-TCPN的拓扑结构,从模型和实例2个层次给出了w-TCPN可调度的判定定理,并描绘了时间约束的修正策略;文献[9]提出了一种基于Parsec的并行计算工作流调度算法;文献[10]进行了基于集群拓扑结构的工作流调度研究;文献[11]针对军事网格应用及工作流的特点,给出一种基于网格工作流分割的调度算法;文献[12]提出了一种基于多QoS目标的工作流任务调度算法;文献[13]对工作流进行了建模与分析。
近些年有关可调度性分析的研究,大部分都基于TCPN,没有加入任何新元素,限制了可调度性分析的应用范围。基于此不足,本文通过引入任务关键系统这一元素,在时间约束着色Petri网(Timing Constraint Color Petri Net,TCCP-Net)中,提出一种任务关键系统的可调度性静态分析、动态分析及其修正策略。
1 TCCP-Net语义及相关概念
1.1 关键任务等级划分
任务关键系统的时间约束验证有两方面要求。一方面,整个工作流过程是在一定时间约束下进行的,文中给出每一个库所的时间约束最大值,即Vpmax。另一方面,将任务根据不同的重要程度分为不同的等级,文中将其分为2个等级。
定义1关键系统中的任务分为关键任务和非关键任务。其中,关键任务是为完成最终任务必须要执行的任务,且每个工作流程中最少要有一个关键任务。
1.2 TCCP-Net定义
定义2时间约束着色Petri网(TCCP-Net)。一个时间约束着色Petri网是一个七元组:TCCP-Net=(P,T,F,M0,C,PT,D)。
1)P:描述系统库所(Place)的有限集合;
2)T:变迁(Transition)的有限集合;
3)F:弧(Arc)的有限集合,满足F⊆(P×T∪T×P);
4)M0:初始变量;
5)C:与每个库所和变迁关联的色彩集。具体地,库所pi的色彩集为C(pi)={ai,1,ai,2,…,ai,ui},其中,ui=C(pi),i=1,2,…,n,变迁tj的色彩集为C(tj)={bj,1,bj,2,…,bj,vj},vj=C(tj),j=1,2,…,m;
6)PT是定义在库所集和变迁集上的整数对PT(pj,tj)=[Vl(pt),Vc(pt)]的集合;
7)D是变迁的执行延迟Vd(t)的集合。
1.3 TCCP-Net中时间参数的形式化定义
图1为一个TCCP-Net的片段,Vl(pt)、Vc(pt)和Td(t)的单位为时间单元,如天(d)、小时(h)等。
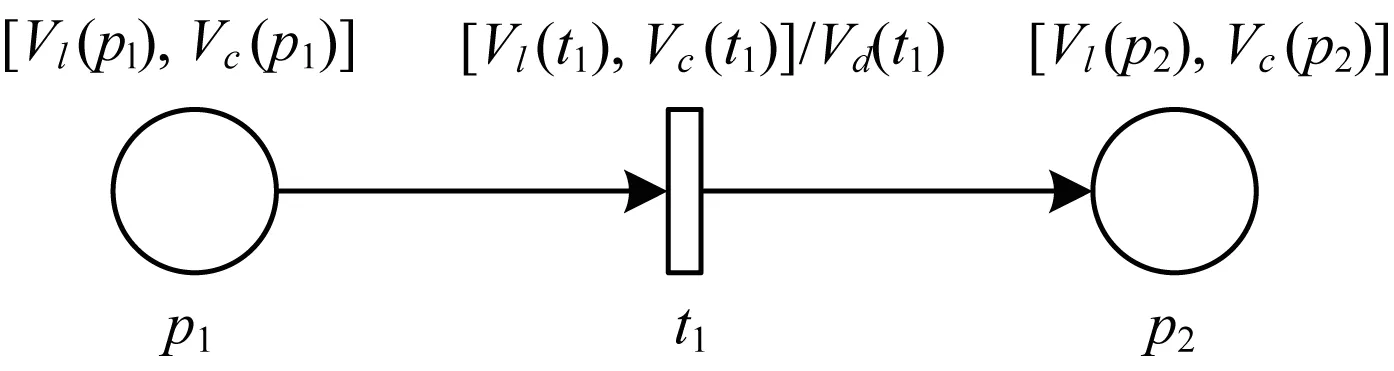
图1 TCCP-Net片段
结合图1,将TCCP-Net中库所和变迁的时间约束条件进行说明,除此之外,为了下文讨论方便,此处给出一些其他变量的定义和运算公式。
1)[Vl(p1),Vc(p1)]和[Vl(p2),Vc(p2)]分别为库所p1和p2上的局部时间约束值,表示库所中的托肯对后续变迁的使能区间。假设托肯到达库所p1的时间为V0,则在区间[V0+Vl(p1),V0+Vc(p1)]内变迁t1被使能。
2)[Vl(t1),Vc(t1)]为变迁t1的局部时间约束值,表示t1的可触发时间。假设变迁t1在V1时刻使能,那么其可触发时间为[V1+Vl(t1),V1+Vc(t1)]。
3)Vd(t1)表示变迁t1完成触发所需要的时间延迟。假设变迁t1的触发时刻为V2,那么完成触发的时刻为V2+Vd(t1)。
4)[EVl(p),EVc(p)]为库所p使能的时间区间,此区间是上文中托肯对后续变迁使能区间的交集。
5)[EVl(t),EVc(t)]为变迁t使能的时间区间。
6)[FVl(t),FVc(t)]为变迁t的可触发时间区间。
7)[FVbegl(t),FVendc(t)]为变迁t触发的最早开始时刻和最晚结束时刻。其中,FVendc(t)=EVc(p)。
8)Token(pn)j为第n个库所中第j个托肯到达的时刻,并且每一个库所托肯的到达时间Token(p)取决于库所中最后一个托肯的到达时间。
由于变迁完成触发还需要一定的时间延迟Vd(t),也就是说如果要求变迁能够成功触发,需要满足条件Vc(t)-Vl(t)≥Vd(t)。
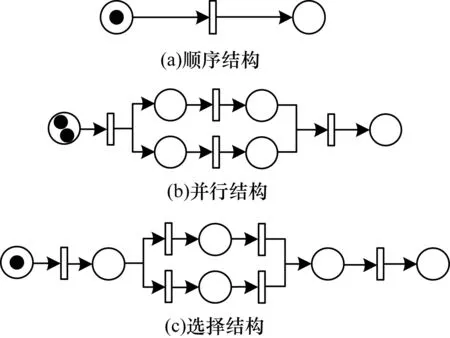
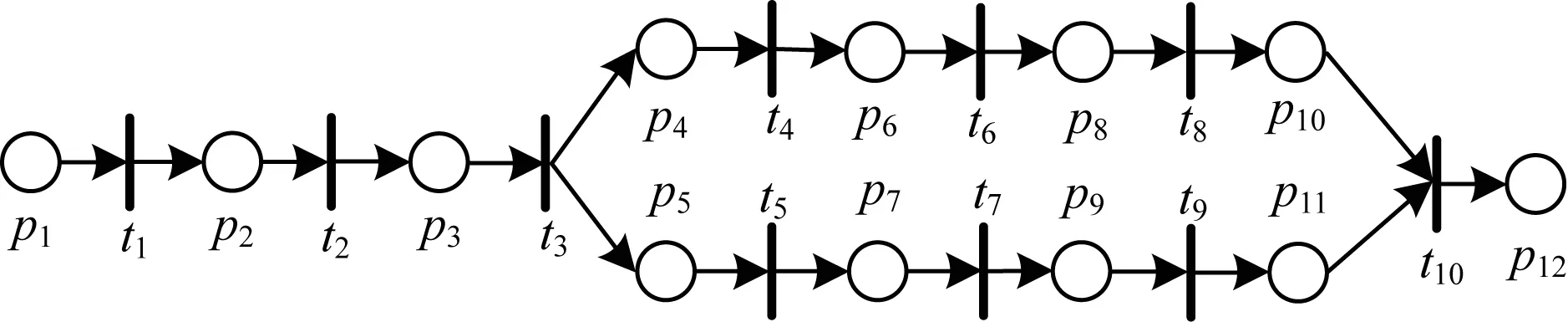
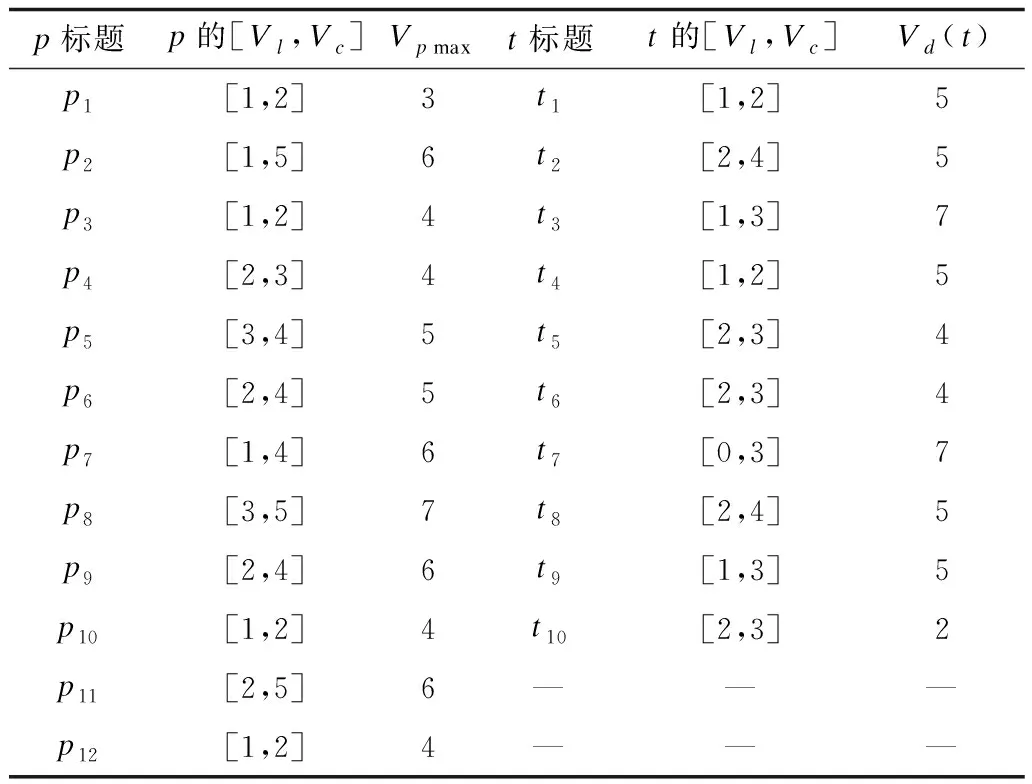
变迁可调度性的验证问题,归根结底是验证变迁触发结束时刻值与出发开始时刻值之差是否满足时间延迟的约束。因此,当变迁的最晚触发结束时刻的值FVendc(t)与最早触发开始时刻的值FVbegl(t)的差值都不满足时间延迟Vd(t)的约束,也即FVendc(t)-FVbegl(t) 规则1在TCCP-Net网的某一状态标识M下,如果变迁t满足: FVendc(t)-FVbel(t)≥Vd(t) (1) 那么变迁t是可调度的。 定义3TCCP-Net网是可调度的,当且仅当网中每一个变迁都是可调度的。 定义4前驱库所(precursor place)。如果有向弧从p连接到t,那么活动t就称为p的前驱库所,即·p。带有m个托肯的库所如图2所示。 图2 带有m个托肯的库所 当只有一个变迁时,若要变迁t进入触发阶段,则需要所有前驱库所都处于使能阶段,也就是说前驱库所中的所有托肯都必须到达,因此,FVbegl(t)和FVendc(t)的计算公式为: FVbegl(t)=FVl(t)=EVl(t)+Vl(t)= min{Token(·p1)m}+Vl(·p)+Vl(t) (2) FVendc(t)=EVc(t)=max{Token(·p1)1}+Vc(·p) (3) 式(2)表示当变迁t处于使能阶段时,需要经过Vl(t)时间才能使得变迁t处于最早触发时间阶段,并且变迁t最早使能时间取决于最后一个托肯的到达时间;式(3)表示当库所处于触发阶段,变迁t处于使能阶段时,必须马上被触发,否则库所中的托肯将会丢失,从而导致变迁无法被触发,并且变迁t最晚使能时间取决于第一个托肯对其使能时间的最大值。 工作流过程的可调度性分析一般分为静态分析和动态分析[14]。其中,静态分析是指不考虑托肯到达库所的时间,动态分析又称强可调度性分析,是指需关注不确定因素对工作流过程带来的影响,其最大的影响因素就是托肯到达库所的时间。 在实际的工作流过程中,只有资源(托肯)全部到达,活动(变迁)才能够被触发,从而使得整个过程得以运行。在分析工作流过程的可调度性时,只有考虑到托肯的到达时间才具有实际意义。因此,文中只对可调度性进行强可调度性分析。 通过规则1可知,变迁的可调度性取决于变迁和前驱库所的时间约束。从图3可以看出,只有并行路径的库所需要大于一个的托肯数。换句话说,只有并行路径存在变迁拥有多个前驱库所的情况。但根据结构可知,其他路径是并行路径的一个特殊情况,因此,只需分析并行路径中多个前驱库所的情况即可。 图3 变迁路径的基本结构 定理1在TCCP-Net网的某一状态标识M下,具有n个前驱库所的变迁强可调度性充要条件为: min{Token(·pi)1}-max{Token(·pi)m}+ minVc(·p)-maxVl(·p)-Vl(t)≥Vd(t) (4) 其中,1≤i≤n。 证明 由于: FVbegl(t)= max{min{Token(·pi)m}+ Vl(·p)}+Vl(t) 其中,1≤i≤n。 FVendc(t)= min{max{Token(·pi)1}+ Vc(·p)} 其中,1≤i≤n,带入式(1)可得: min{ max{Token(·pi)1}+Vc(·p)}- max{min{Token(·pi)m}+ Vl(·p)}+Vl(t)≥Vd(t) 也即: min{ max{Token(·pi)1}}- max{min{Token(·pi)m}+minVc(·p)- maxVl(·p)-Vl(t)≥Vd(t) 其中,1≤i≤n,式(4)得证。 综上所述,工作流过程的可调度性分析的基本思路为:根据已知时间约束,计算变迁t触发最早开始时刻FVbegl(t)和最晚结束时刻FVendc(t)的值,然后比较FVendc(t)-FVbegl(t)≥Vd(t)是否成立。若成立,则可判断t是强可调度的;若不成立,则应对变迁及其前驱库所的时间约束进行修正,从而使得变迁为强可调度的。 工作流过程的可调度分析不仅要验证工作流中的变迁是否可调度,还要对不可调度的变迁进行修正,使得整个工作流网都为可调度的。由式(4)可知,影响变迁可调度性的元素有4种:库所使能时间上限,库所使能时间下限,变迁可触发时间下限和变迁完成触发所需的时间延迟。其中,时间延迟是固定值,无法进行修改。那么,如果要使得式(4)成立,根据对工作流过程的总的时间约束值Vpmax,可首先减小变迁可触发时间下限值;若仍不成立且V≤Vpmax,则可减小库所使能时间下限值并增加库所使能时间上限值;最后,若式(4)仍不成立且V≥Vpmax,则根据关键任务的等级程度对其进行取消执行。假设工作流时间约束为Vpmax,当V≤Vpmax时,具体步骤如下: 步骤1减小Vl(t)的值,如果Vl(t)≥0且式(4)成立,转入步骤4,否则转入步骤2。 步骤2减小Vl(·p)的值,如果Vl(·p)≥0且式(4)成立,转入步骤4,否则转入步骤3。 步骤3寻找变迁t的直接前驱库所·p,增加Vc(·p)的值,当式(4)成立,但V(·p)>V(·pmax)时,若活动t为非关键任务,则可直接取消执行任务t;若活动t为关键任务,则增大Tmax的值,直到式(4)成立。 步骤4结束。 图4为某港岸基保障信息系统流程,码头一般设置有食品供应中心、供水中心、供电中心、供暖中心等岸基保障设施,所以舰艇靠岸驻泊后,岸基保障部门通过这些保障设施为其补给水、电、气、食品以及军械、弹药等物资[15],其工作流程如图4所示。其中:p1表示准备提交申请;p2表示准备进行审核;p3表示完成审核,准备部门批准;p4表示完成批准,准备配备食品;p5表示完成批准,准备配备水电;p6表示准备调用货车;p7表示准备调配保障人员;p8表示食品装配完毕,待运输;p9表示水电准备完毕,待配送;p10表示食品输送完毕,待确认;p11表示水电配送完毕,待确认;p12表示水电配送完毕,待确认;t1表示提交申请;t2表示部门进行审核;t3表示部门批准;t4表示配备需供应的食品;t5表示配备需供应的水电;t6表示将货车调到食品供应站;t7表示调用保障人员;t8表示用货车运输食品;t9表示保障人员进行水电配送;t10表示确认任务完成。 图4 案例工作流程 案例工作流程时间约束集PT如表1所示,其时间单位为min。 表1 案例工作流程时间约束集 一只舰艇靠岸驻泊后,假设库所p中有2个托肯,到达库所的时间区间分别为:Token(p)1=[1,3]和Token(p)2=[2,5],且t4~t9为关键任务,t1~t3、t10为非关键任务。运用第2节所述的工作流过程,可调度性验证方法对案例进行验证的过程如下: 1)对活动t1进行验证,其最早触发开始时间值与最晚触发结束时间值分别为: FVbegl(t1)= min{Token(·p1)2}+Vl(·p1)+ Vl(t1)=4 FVendc(t1)= max{Token(·p1)1}+ Vc(·p1)=5 由于FVendc(t1)-FVbegl(t1)=1<5,对活动t1的时间约束进行修正: (1)减小Vl(t1)的值至0,则FVendc(t1)-FVbegl(t1)=2<5,活动仍不可调度约束。此时,活动t1新的时间约束为[0,2]。 (2)减小Vl(·p1)的值至0,则FVendc(t1)-FVbegl(t1)=3<5,活动仍不可调度约束。此时,库所p1新的时间约束为[0,2]。 (3)若要使得FVendc(t1)-FVbegl(t1)≥5,FVbegl(t1)的最小值为2,那么就需要增加FVendc(t1)的值,由上述分析可知增加Vc(·p1)的值为4时,不等式成立。此时库所p1新的时间约束为[0,4]。但由已知条件可知,V(p1)max=3,并且活动t1为非关键任务,因此,可选择不执行活动t1,直接执行活动t2。 2)对活动t2进行验证: FVbegl(t2)= min{Token(·p2)2}+ Vl(·p2)+Vl(t2)=3 FVendc(t2)= max{Token(·p2)1}+ Vc(·p2)=8 由于FVendc(t2)-FVbegl(t2)=6>5,因此活动t2为可调度的。 3)对活动t3进行验证: FVbegl(t3)= min{Token(·p3)2}+Vl(·p3)+ Vl(t3)=9 FVendc(t3)= max{Token(·p3)1}+ Vc(·p3)=15 由于FVendc(t3)-FVbegl(t3)=6<7,因此对活动t3的时间约束进行修正: (1)减小Vl(t3)的值至0,则FVendc(t3)-FVbegl(t3)=7,可调度。 (2)活动t3新的时间约束为[0,3],活动t3新的最早触发开始时间值与最晚触发结束时间值分别为: Vl(·p3)+Vl(t3)=8 4)对活动t4进行验证: FVbegl(t4)= min{Token(·p4)2}+ Vl(·p4)+Vl(t4)=18 FVendc(t4)= max{Token(·p4)1}+ Vc(·p4)=25 由于FVendc(t4)-FVbegl(t4)=7≥5,因此活动t4为可调度的。 5)对活动t5进行验证: FVbegl(t5)= min{Token(·p5)2}+ Vl(·p5)+Vl(t5)=28 FVendc(t5)= max{Token(·p5)1}+ Vc(·p5)=34 由于FVendc(t5)-FVbegl(t5)=6>4,因此活动t5为可调度的。 6)对活动t6进行验证: FVbegl(t6)= min{Token(·p6)2}+ Vl(·p6)+Vl(t6)=37 FVendc(t6)= max{Token(·p6)1}+ Vc(·p6)=42 由于FVendc(t6)-FVbegl(t6)=5≥4,因此活动t6为可调度的。 7)对活动t7进行验证: FVbegl(t7)= min{Token(·p7)2}+ Vl(·p7)+Vl(t7)=42 FVendc(t7)= max{Token(·p7)1}+ Vc(·p7)=50 由于FVendc(t7)-FVbegl(t7)=8≥7,因此活动t7为可调度的。 8)对活动t8进行验证: FVbegl(t8)= min{Token(·p8)2}+Vl(·p8)+ Vl(t8)=54 FVendc(t8)=max{Token(·p8)1}+Vc(·p8)=62 由于FVendc(t8)-FVbegl(t8)=6≥5,因此活动t8为可调度的。 9)对活动t9进行验证: FVbegl(t9)= min{Token(·p9)2}+Vl(·p9)+ Vl(t9)=62 FVendc(t9)= max{Token(·p9)1}+ Vc(·p9)=71 由于FVendc(t9)-FVbegl(t9)=9≥5,因此活动t9为可调度的。 10)对活动t10进行验证: FVbegl(t10)= min{Token(·p10)2}+ Vl(·p10)+Vl(t10)=70 FVendc(t10)= max{Token(·p10)1}+ Vc(·p10)=78 由于FVendc(t10)-FVbegl(t10)=8≥7,因此活动t10为可调度的。 11)验证算法结束。 对不可调度的活动进行修正后的时间约束值如表2所示。其中“/”表示无数据。 表2 修正后的时间约束值 为了更好地解决时间约束下工作流过程的可调度性分析这一问题,本文引入了时间约束Petri网,将工作流中的活动分为关键任务和非关键任务,提出了可调度性分析的判别方法,并且对于不可调度的活动进行时间约束修正,从而使得整个工作流满足可调度性。分析结果表明,该方法不仅增强了工作流运行的准确性,还大幅提高了其运行效率。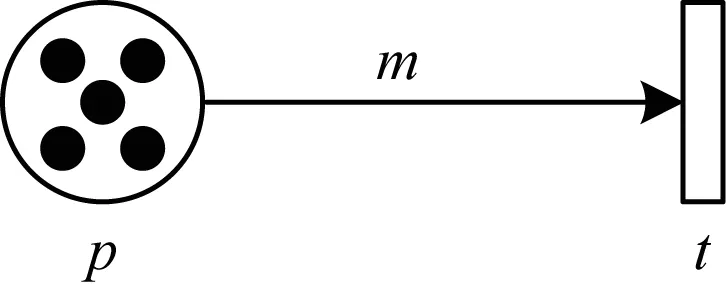
2 时间约束下的CTPN可调度性分析
2.1 可调度性分析方法
2.2 时间约束修正策略与算法
3 案例分析

4 结束语

