前向纠错算法的研究

肖利平

(贵州理工学院，贵州 贵阳 550003)

0 引言

在现代通信过程中，差错控制方法主要有3种:自动请求重发技术、反馈校验技术和前向纠错技术。

自动请求重发技术就是当接收端所接收的信息码有错时，请求发送端重新发送该组信息码。

反馈校验法就是接收端接收到的信息后，无论其正确与否，都无条件地将接收到的信息码原原本本地送回到发送端，由发送端进行判断，若不正确，则自动重发该组信息码。

前向纠错技术的基本思想是，接收端不仅能对数据进行错误判断，而且还能对错误进行定位，从而能自动进行纠错。纠错时，将错误位求反即可。

本文研究的就是第三种差错控制方法，即前向纠错算法。

2 前向纠错算法

2.1 逻辑异或运算

逻辑异或运算符通常用“⊕”表示。其运算规则是，相同两数码异或结果得0，不同两数码异或结果得1。

2.2 算法描述

2.2.1 校验码及校验公式

算法的设计思路是，每组传输信息由8个数码位＋8个校验位组成，即一个传输信息组共16位，依次用B1～B16表示。

B9～B16的计算式:

2.2.2 校验方法

在发送端，用(1)～(8)式计算出校验码B9～B16，连同前8位信息码一道发出；在接收端，用(9)～(16)式进行校验，若这8个式子的计算结果都为0，则说明传输正确，只要有一个式子的计算结果为1，则说明传输有错。

2.2.3 判断法则

法则1:若(9)～(16)式子全错，则B1必错；

法则2:若只有(10)式正确而其余7个式子全错，则B2必错；

法则3:若只有(11)式正确而其余7个式子全错，则B3必错；

法则4:若只有(12)式正确而其余7个式子全错，则B4必错；

法则5:若只有(13)式正确而其余7个式子全错，则B5必错；

法则6:若只有(14)式正确而其余7个式子全错，则B6必错；

法则7:若只有(15)式正确而其余7个式子全错，则B7必错；

法则8:若只有(16)式正确而其余7个式子全错，则B8必错；

法则9:若只有(9)式错而其余7个式子正确，则B9必错；

法则10:若只有(10)式错而其余7个式子正确，则B10必错；

法则11:若只有(11)式错而其余7个式子正确，则B11必错；

法则12:若只有(12)式错而其余7个式子正确，则B12必错。

法则13:若只有(13)式错而其余7个式子正确，则B13必错；

法则14:若只有(14)式错而其余7个式子正确，则B14必错；

法则15:若只有(15)式错而其余7个式子正确，则B15必错；

法则16:若只有(16)式错而其余7个式子正确，则B16必错。

2.2.4 算法的证明

在这里，我们采用反证法进行证明。

由于篇幅所限，本文只证明第一种情况:即当(9)～(16)式全错时，B1必错，而其他位正确。

假设(9)～(16)式全错，而B1正确，则B2～B16必有一位错。

假设B2错，而B1，B3～B16正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(10)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B2不可能有错。

假设B3错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(11)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B3不可能有错。

假设B4错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(12)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B4不可能有错。

假设B5错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(13)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B5不可能有错。

假设B6错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(14)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B6不可能有错。

假设B7错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(15)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B7不可能有错。

假设B8错，而其余位正确，将其代入(9)～(16)式:

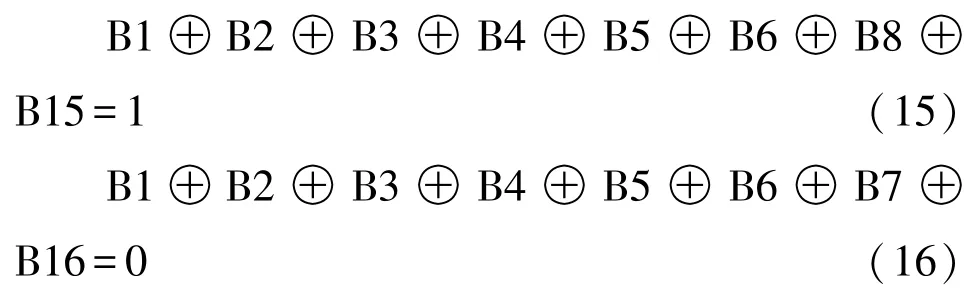
从上述计算结果可看出，只有(16)式正确而其余式全错，与“(9)～(16)式全错”相矛盾，因此，B8不可能有错。

假设B9错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(9)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B9不可能有错。

假设B10错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(10)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B10不可能有错。

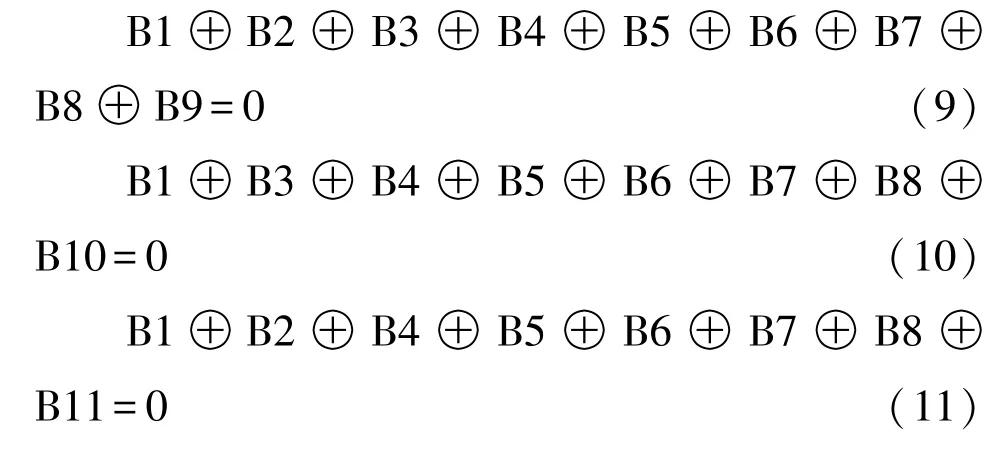
假设B11错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(11)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B11不可能有错。

假设B12错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(12)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B12不可能有错。

假设B13错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(13)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B13不可能有错。

假设B14错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(14)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B14不可能有错。

假设B15错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(15)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B15不可能有错。

假设B16错，而其余位正确，将其代入(9)～(16)式:

从上述计算结果可看出，只有(16)式错而其余式正确，与“(9)～(16)式全错”相矛盾，因此，B16不可能有错。

由上证明过程可看出，在(9)～(16)式全错的情况下，B2～B16都不可能有错，因此，必有B1错。

证毕。

同理，可证明其他15种情况。

3 结语

本算法显著的优点是:每组发送的信息码为8个二进制位，而标准的ASCII码每个字符的长度也正好是8位，因此，每次可发送一个完整的字符，这正符合现代计算机网络通信规范。算法存在的主要不足是:信息的传输量要增加一倍。如何压缩校验位的长度，值得继续研究。

在实际网络通信过程，纠错时只需要判断前8位B1～B8的正确性，而后8位B9～B16是不必判断的，这样可节省差错判断的时间，以提高通信数据处理能力。