基于梁截面几何特性参数的白车身结构优化设计

赵永宏，陈东，袁焕泉，耿富荣，熊志华，汪芳胜



基于梁截面几何特性参数的白车身结构优化设计

赵永宏，陈东，袁焕泉，耿富荣，熊志华，汪芳胜

（广州汽车集团股份有限公司汽车工程研究院，广东 广州 511434）

文章建立了基于梁截面几何特性参数的参数化车身概念模型，提出车身刚度相关性系数对梁与壳单元转换产生的精度误差进行修正。同时，引入Kuhn-Tucker约束条件，以梁的质量最小值为目标函数，车身弯曲、扭转刚度目标值为约束函数，输出最优的梁截面几何特性参数结果，进而确定截面形状及其几何尺寸。另外，对各车身梁结构的性能贡献度进行了分析，在满足车身扭转、弯曲刚度性能目标的基础上，对参考车型结构进行优化，使得车身减重36.4kg，减轻率为11.9%。

车身；参数优化；性能；梁结构

前言

在车身概念设计阶段，有针对性地控制车身结构力学性能（刚度、模态等），可以极大程度地提高设计的可靠性、缩短车身开发周期[1-2]。作为主要的承载构件，车身结构中梁的占比最大，其结构设计的合理与否更是直接影响着车身后续阶段的开发进程[3-4]。因此，在车身概念设计中，基于车身性能目标的定义，梁的结构优化显得尤为重要。

关于车身概念设计阶段梁结构的优化设计研究层出不穷，涌现了多种优化模型和设计方法。Nishigaki等人开发了First Order Analysis系统，用于简化车身梁、接头结构的性能优化分析[5-6]。德国SFE公司采用隐式参数化技术开发了SFE-CONCEPT商业软件，通过建立几何、网格一体化模型，实现了车身结构的形状、厚度和位置的快速优化分析[7]。VOLVO汽车公司提出了Property Based Models（PBM）车身设计方法，在概念阶段建立梁、接头和面板结合的参数化模型，可用于车身性能的预测与优化[7-8]。侯文彬等开发的VCD _ICAE系统，直接建立车身概念结构，进行了梁截面形状尺寸的优化设计[9-10]。

目前，关于车身梁的结构优化设计方法多种多样，但多是通过梁结构本身尺寸和形状的改进和优化以间接追求车身整体的性能目标，而通过对梁截面几何特性参数（惯性矩、扭转常数等）的优化来改进梁结构的力学性能，进而车身性能的研究策略却鲜有报道。

本文基于参数化的技术思想，采用梁单元对车身结构进行建模，引入刚度相关性系数用于消除梁壳转换造成的误差，并结合梁结构性能贡献度及车身性能目标的要求，对梁截面几何特性参数进行优化，进而确定截面形状及其几何尺寸，实现车身结构的减重。研究结果对提高新车型概念设计阶段的开发效率及轻量化设计具有重要的意义。

1 参数化车身模型的建立

基于参数化的技术思想，对车身进行建模，主要包括梁、接头和面板等结构。其中，面板结构主要分布于顶盖、地板和侧围位置，以保证参数化车身模型的稳定性，使其刚度性能与实际车身有更好的一致性；接头结构由梁结构的连接形成，主要用于梁结构之间的载荷传递，由于接头在车身结构中起着关键性作用，在设计时又主要取决于梁的结构特点和刚度性能，故接头不做特殊处理，保持壳单元结构，以保证梁截面特性的优化精度。

图1 参数化车身模型

图2 薄壳梁截面示意图

1.1 梁截面参数定义

基于有限元思想，在车身参数化模型中，采用一维梁单元进行建模，在商用软件NASTRAN中采用CBEAM单元定义[11]，梁的截面几何特性参数通过PBEAM关键字定义，包括材料面积，截面惯性矩I、I，极惯性矩I和扭转常数。梁截面内薄壁可离散为多个小线段，如图2所示，其几何特性参数计算公式如下：

梁截面面积：

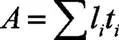
梁截面形心坐标：

梁截面惯性矩和极惯性矩：

闭口、开口截面梁扭转常数为：

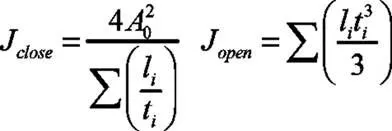
式中，l为截面边界分割后的小线段长度，t为截面边界材料厚度，为梁截面材料面积，A为截面边界分割后小线段面积，c、c为小线段中心分别到基于截面形心的垂直坐标系、轴的垂直距离，α是边界小线段与轴正向的夹角，0为截面边界所围成的面积。

由公式（1）～（4）可知，梁截面几何特性参数主要与截面材料面积和材料到形心的距离有关，所以截面形状设计主要考虑边界的周长、料厚和边界到形心坐标系、轴的垂直距离c、c。

1.2 刚度相关性系数

车身结构中的梁结构由薄壳焊接而成，而一维梁单元截面沿轴向具有均匀性的特点，并不能充分体现壳的局部变形特性，这些差异将导致框架梁车身刚度与实际车身产生偏差。这里设定车身刚度性能相关系数用与评价车身的等效精度，其公式如下：

式中：为相关性系数，K为参考车身刚度，K为等效梁单元车身（概念车身）刚度。

2 几何特性参数优化

车身梁结构优化的主要目的是在保证车身结构力学性能的前提下，尽可能地减少车身梁截面材料的盈余，从而降低车身的整体质量，提高车身概念模型的可靠性与合理性。

2.1 优化方法

优化方法采用NASTRAN基于结构参数的优化方法[12]，其数学表达式如下：

目标函数：

约束函数：

边界条件：

设计变量：

其中，目标函数是一个由设计变量表示的标量函数，优化目的是求目标函数的最小值；约束函数表达式定义为小于等于0的不等式，即约束函数为负值，阀值为0；边界条件限定设计变量的变化范围。

优化问题的求解采用两个约束条件的Kuhn-Tucker优化策略，如图3所示。目标函数()，约束函数1()、2()，约束边界是两个约束函数等于0值时的曲线。目标函数是一组常数绘制的轮廓钱，目标函数的方向沿着轮廓线的峰顶方向。目标函数的最优值为两条约束边界线的交点位置，即图示中的X处。

图3 两个约束条件的Kuhn-Tucker优化策略

2.2 优化变量

框架车身模型刚度由梁单元的刚度特性决定。其中，梁单元的轴向刚度为弹性模量和面积的乘积，即；弯曲刚度为截面的惯性矩和材料弹性模量的乘积，即EI、EI；扭转刚度为剪切模量和扭转常数的乘积，即。因此，本文将梁截面力学参数、I、I和作为优化变量，从而定义优化设计空间，实现车身梁结构优化的目的。这些参数变化范围下限为其初始值的10%，上限则为其初始值的200%，即：

2.3 目标函数

一维梁单元的质量为截面面积和长度的乘积，即。根据框架车身梁结构优化的目的，实现梁单元的质量最小，其数学表达式如下：

式中，A为梁单元截面面积，L为梁单元的长度，为材料密度。

梁的长度由车身结构的空间布置决定，变化幅度很小，所以梁结构质量的降低主要由减小梁截面面积来实现。

2.4 约束函数

本文车身刚度性能主要考虑静态扭转刚度和静态弯曲刚度。刚度性能指标在优化中定义为约束函数。图4给出车身扭转、弯曲两种工况下的受力特点及位移测点。

图4 扭转、弯曲载荷工况

扭转工况为在轴心位置对应的塔座支撑点施加扭矩，测量左右加载点相对扭转角度，扭转刚度K计算公式如下：

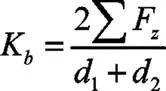
刚度约束函数定义为：

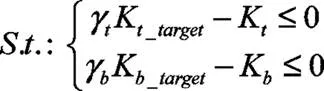
式中，K为车身扭转刚度目标值；K为弯曲刚度目标值，γ、γ为根据公式（5）计算出的概念车身和详细壳单元模型的扭转、弯曲刚度相关性系数。

表1 A柱上边梁梁截面几何参数优化结果

3 车身梁结构优化设计实例

以某参考车白车身为例，建立梁框架车身模型，该模型要优化的梁结构有18个，每个梁分别对应着一个梁截面。概念车身模型与参考车身的扭转刚度相关性系数为98.2%，弯曲刚度相关系数99.85%。车身扭转刚度目标定义为16000 Nm/°，弯曲刚度目标定义为18000N/m。利用前述优化方法，以车身质量最小化为目标函数，车身扭转、弯曲刚度为约束函数，梁截面参数为设计变量，进行梁结构优化，计算输出各个梁截面最优的几何特性参数。

表1为框架车身A柱上边梁优化前后梁截面几何特性参数在优化前后的结果对比，可知优化后的梁截面参数比初始值有相对减少。根据截面几何特性参数的变化情况、车身A柱上边梁的实际功能以及工艺要求等对截面进行重新设计，如图5所示。设计后的截面比参考截面面积减少24.13%。

表2 车身梁截面参数优化与设计结果汇总

同理，对其余梁结构的截面进行优化设计，设计时综合考虑工艺和车身造型、布置的影响，使设计的截面参数尽可能满足优化值。各个梁截面前后优化对比如表2所示，仔细观察发现，少数梁结构的截面几何特性中个别参数在优化过程中呈增大趋势，其余大部分梁结构的几何特性都有不同程度的减少，这就为整体车身结构的减重创造了条件，可以在各个梁截面的面积变化中看出，各几何特性参数的优化结果，为之后的截面设计提供了方向指引。

另外，为了便于分析各个梁结构几何特性参数在优化过程中对结构性能及车身整体的影响，这里分析了各个梁结构性能变化的灵敏度及其对车身整体性能的影响，见图6。在图6(a)中，各个梁结构几何特性参数所引起的自身性能的变化灵敏度有显著差异，且各个梁结构对不同性能的贡献不同。图6(c) 则给出了各结构性能变化对车身整体结构的影响，在对车身结构进行优化时可据此针对不同梁结构部件进行优化，使得方向更加清晰，结果易于控制。

然而，考虑到各个梁结构及车身性能目标数目可能比较多，在对各结构及车身进行性能评估时，结果比较分散，不便于分析。因此，这里采用求均方值的方法对各性能进行综合考虑，如图6(b)和6(d)所示，从图中可以得出各梁结构整体性能的灵敏度及其对车身整体的贡献度。

图5 A柱上边梁截面优化设计

图6 各梁结构性能变化及对整车性能的影响

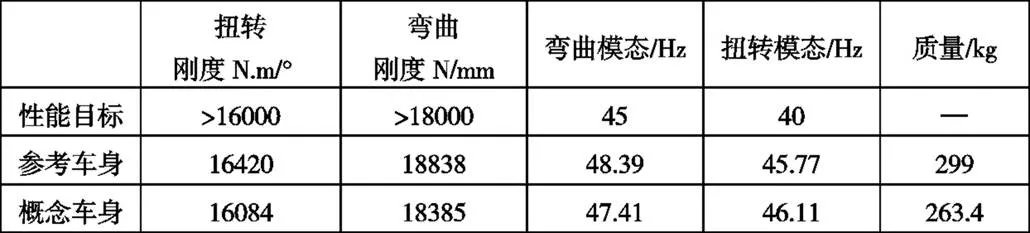
根据新设计的截面参数进行概念数据设计，得到车身的概念模型质量和刚度性能满足目标要求，车身各性能计算结果如表3所示，计算得到概念车身质量相对参考车身减少11.9%，即36.4kg。

表3 新概念车身性能计算结果

4 结束语

基于有限元思想建立了参数化的车身结构模型，利用Kuhn-Tucker约束优化策略，以车身梁结构质量最小化为目标，弯曲、扭转刚度为约束，梁截面几何特性参数为变量，对模型参数进行了优化计算。根据优化结果，在综合考虑造型、工艺和布置的情况下对梁结构的截面进行针对性的设计，进而完成新车型的概念设计。同时，也分析了各梁结构在几何特性参数变化时结构的性能灵敏度，揭露了各结构性能在车身整体性能中的贡献度，并采用求均方值的方法对不同性能进行综合评估，研究结果为车身结构优化及轻量化提供重要的参考依据。经优化设计后的新车身刚度性能满足目标要求，质量减少36.4kg，减轻率为11.9%。

[1] 左文杰.简化车身框架结构建模与快速优化研究[D].吉林大学, 2010.

[2] 徐涛,左文杰,徐天爽,等.概念车身框架结构的多变量截面参数优化[J].汽车工程, 2010, (05): 394-398+428.

[3] 郭润清,侯文彬,胡平,等.车身轻量化中梁截面优化的研究与实现[J].汽车工程, 2012, (01): 40-45.

[4] 孔敏,郭永进,刘波.轿车白车身概念设计阶段梁截面优化设计[J]. 机械设计与研究,2010,(06): 120-123.

[5] Hidekazu Nishigaki, Tatsuyuki Amago,Hideki Sugiura, et al. First order analysis for automotive body structure design–Part 1: Overv -iew and applications[J]. SAE TECHNICAL PAPER SERIES, 2004, 01-1658.

[6] Hidekazu Nishigaki, Shinji Nishiwaki, Tatsuyuki Amago, et al. First order analysis - new CAE tools for automotive body designers [J]. SAE TECHNICAL PAPER SERIES,2001,01-0768.

[7] Hans Zimmer, U. Umlauf, Jack E. Thompson,et al. Use of SFE CONCEPT in developing FEA models without CAD[J]. SAE TECH -NICAL PAPER SERIES,2000,01-2706.

[8] Nicklas Bylund, Magnus Eriksson, Simulation Driven. Car body development using property based models[J].SAE TECHNICAL PAPER SERIES,2001,01-3046.

[9] 侯文彬,王增飞,张伟,等.基于复杂工程约束的车身梁截面优化设计[J].机械工程学报, 2014, (18): 127-133.

[10] 胡平,郭润清,侯文彬,等.概念车身梁截面厚度优化设计[J].汽车技术,2011, (10): 1-5.

[11] MD Nastran Linear Statics Analysis User’s Guide[M]. MSC. Software Corporation, June 2010 Reversion 0.

[12] MD Nastran Design Sensitivity and Optimization User’s Guide[M]. MSC. Software Corporation, June 2010 Reversion 0.

Optimization of car-body structures based on the characteristic parameters of beam structures

Zhao Yonghong, Chen Dong, Yuan Huanquan, Geng Furong, Xiong Zhihua, Wang Fangsheng

( Guangzhou Automobile Group Co., Ltd Automotive Engineering Institute, Guangdong Guangzhou 511434 )

In this paper the parametric technique is utilized for the conceptual design and optimization of car body with stiffness analysis. According to the finite element theory the reference car body is parameterized using beam elements. The correlation coefficient of stiffness is defined to modify the precision of computational model. In the optimization process, the minimum mass is defined as objective function, values of the flexural and torsional stiffness are regarded as the constraint functions. Then, with the Kuhn-Tucker condition the optimal parameters of geometric characteristic can be obtained for the determination of shapes and sizes of beam cross sections. Besides, the effect of beam structures on performances of car body is analyzed in detail and after the optimization the mass decreases by 11.9 % (36.4 kg).

Car-body; parametric optimization; performance; beam

B

1671-7988(2018)24-135-05

U462

B

1671-7988(2018)24-135-05

U462

赵永宏，高级工程师，研究方向主要为车身性能及结构轻量化。

10.16638/j.cnki.1671-7988.2018.24.049