车用燃料电池离心式空压机叶轮多参数多工况优化*

展庆，章月朦，许思传



车用燃料电池离心式空压机叶轮多参数多工况优化*

展庆，章月朦，许思传

（同济大学汽车学院，上海 201804）

离心式空压机耗功占燃料电池输出功率的20%左右。为了提高燃料电池在整个车用工况的效率，文章将多岛遗传算法与数值仿真相结合，提出了一种离心空压机多工况多参数的优化方法。文章基于NEDC(New European Driving Cycle)工况针对车用空压机两个常用工况，以各工况下的压比以及整机的喘振和阻塞边界为约束条件，选取叶片叶尖进口安装角、叶片叶底进口安装角、叶片进口直径、出口宽度、出口直径、出口安装角以及扩压器长度7个关键参数作为优化变量，对各工况的效率进行寻优。对比原始设计方案，优化后的叶轮流道内的流动更加稳定，低速涡团和逆流区明显减少，损失降低；在两个工况的效率分别提高了3%和4%。

燃料电池；离心式空压机；多工况多目标；多岛遗传算法

引言

随着能源问题和环境问题的加剧，国家的排放法规日益严格，汽车行业正经历巨大的变革，各国政府和企业都在不断倡导发展新能源汽车。其中，燃料电池汽车由于其由于具有续驶里程长、加氢时间短等锂电池汽车不具备的优势，在排放、效率等方面也明显优于传统内燃机汽车，因此燃料电池汽车在新能源汽车占据重要地位[1]。

燃料电池系统主要由电堆、空气供应系统、氢气供应系统和水热管理系统组成。空气压缩机是燃料电池空气供给系统的核心部件，它将反应所需的空气压缩至电堆反应所需的压力，这对提高燃料电池的功率密度和效率，减小燃料电池电堆尺寸有重要作用。由于汽车运行工况比较复杂，因此要求空压机能够根据电堆需求及时进行供气调节，而且在燃料电池系统的辅助部件之中，空气压缩机的寄生功耗很大，约占燃料电池辅助功耗的80%[2]。所以，燃料电池用压缩机的设计对燃料电池系统意义重大。

离心叶轮作为空压机的主要部件，其设计的优良与否对空压机的性能有着至关重要的影响。针对离心叶轮的优化，前人提出了很多优化方法。Engeda A[3]等人根据经验对叶轮进出口参数进行横向比较，给出了不同策略的优化方案，然后采用仿真和试验相结合的方式对各种优化方案进行验证，最终得到最优的一组进出口参数。JinTang[4]等分析了叶顶间隙、分流叶片位置、叶片扭曲等因素对空压机性能的影响。该优化方法效率较高，但需要设计者对叶轮参数对性能的影响规律有清晰的认识，非常依赖设计经验。汪创华[5]等人分析了长、短叶片的相对位置对离心压缩机性能的影响，并通过数值计算验证提出了改进通道涡和二次流的设计方案。

由于离心叶轮的控制参数较多且各参数之间相互耦合，共同影响空压机的性能，任意参数的改变对性能的影响非常复杂，因此，算法优化的优势就体现了出来。韦开君[6]等分析了叶片进口角、叶片出口角等参数对离心压缩机压比和绝热效率的影响，通过建立Kriging模型对压缩机进行优化设计，设计工况点的压比和效率有所提高；张良[6]等结合均匀设计法、神经网络模型以及多目标遗传算法，对离心叶轮的多个参数进行了优化设计，优化后等熵效率和静圧比都有所提高。王文杰[8]等针对泵叶轮提出了一种基于Kriging近似模型和遗传算法的优化方法针对叶轮的多个参数进行优化，优化后的叶轮效率在两工况下的效率都有所提高。算法优化大多采用的方法是通过建立近似模型，在近似模型上进行寻优以期能够得到最优结构。但该方法存在以下问题：一方面，模型的精度难以保证，为了不使模型过拟合而又有足够的泛化能力，参与训练的样本数要足够多；另一方面，近似模型的寻优结果没有经过流体流动仿真，往往不能符合实际的流动情况，即所得到的优化结果很有可能使流动模型更加恶化。

本文根据车用燃料电池空压机运行的多个工况，通过驱动脚本使得设计软件和仿真软件能够自动进行叶轮的设计和仿真，使用优化算法对仿真结果进行筛选处理，然后生成下一组设计参数，重复运行以上过程直至寻至最优解。该设计方法可以充分利用算法优化的优势，由仿真得到的最优结构也能符合流体流动规律，且该方法大大减少了时间成本，使得设计效率大大提高。

1 离心式空压机多参数多工况优化

本文选取在叶轮设计中两个性能指标——效率作为设计目标、压比作为约束条件。在满足空压机喘振和阻塞边界的要求下，选取了两个常用工况点作为优化的工况，采用多岛遗传算法和数值仿真相结合的方法，对包括叶轮出口宽度b2、出口直径d2、出口安装角β2等七个主要的结构参数进行了优化。

由于叶轮设计参数较多，各个参数相互耦合，优化目标之间存在相互制约，所以采用传统的优化方法很难找到全局最优解。多岛遗传算法以生物进化为原型，具有很好的收敛型，其具有计算时间少，鲁棒性高等优点。它不但能够找到全局最优解，而且简单的逻辑结构利于程序设计，能够大大减少设计人员的工作量。

1.1 优化方法

遗传算法是模拟生物在自然界中遗传和进化过程中而形成的一种自适应全局优化概率搜索算法[9]。遗传算法对决策变量进行编码，使其成为“染色体”的形式，通过模拟染色体间的选择、交叉、变异等行为，根据个体的适应度来找寻具有最优性状的“个体”，但其缺点在于可能会出现“早熟”现象，使优化结果陷入局部最优解。

多岛遗传算法是在传统遗传算法的基础上发展起来的，其进化过程如图1所示。多岛遗传算法和传统遗传算法的不同在于整个种群分布在多个“岛屿”上，各个岛屿间相互隔绝，每个子群独立进化。除此以外，各个岛屿间以一定的时间间隔进行“迁移”操作，完成了各个独立“岛屿”岛屿之间的信息交换。多岛遗传算法能够有效提高运算速度，若干独立进化的子群也增加了整个种群的多样性，抑制了“早熟”现象的发生，更容易找到全局最优解0。

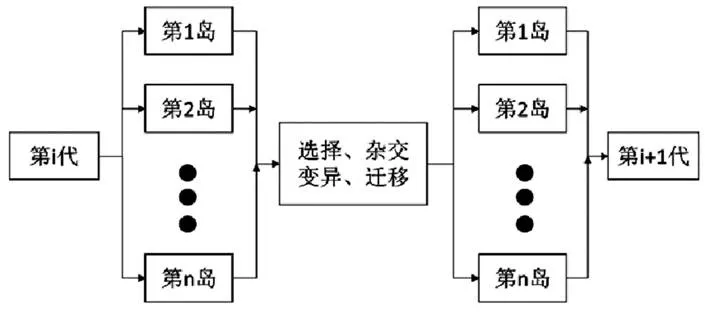
图1 多岛遗传算法

1.2 模型参数

图2 离心叶轮结构

本文的优化对象是单级离心式空气压缩机，其叶轮结构如图2所示。本文选取的叶轮优化参数有：叶轮进口叶底安装角（β1h），叶轮进口叶顶安装角（β1s），叶片出口安装角（β2），叶轮出口直径（D2），叶片出口直径（Ds），叶轮出口宽度（B2）和扩压器长度（Ls）。

1.2.1求解器设置

在求解器中针对叶轮单流道性能进行仿真计算，流体介质假设为理想气体，选取SST k-ω湍流模型。进口边界条件为压力入口，出口边界条件为流量出口，进口压力设置为101 kPa。定子保持静止，叶片和轮毂以给定转速旋转，所有固体壁面均采用无滑移、绝热边界。该模型采用二阶迎风差分格式对各项进行离散，当计算残差低于10-6时认为仿真收敛。

1.2.2模型验证

为了验证仿真模型的可靠性，对已有空压机进行了台架试验，测试台架可以实时测量采集离心空压机流量、压比、进出口温度、进出口压力等参数。在给定转速下，通过调节出口阀门开度得到压比随质量流量的变化。图3给出了不同转速下试验与仿真值的对比结果。

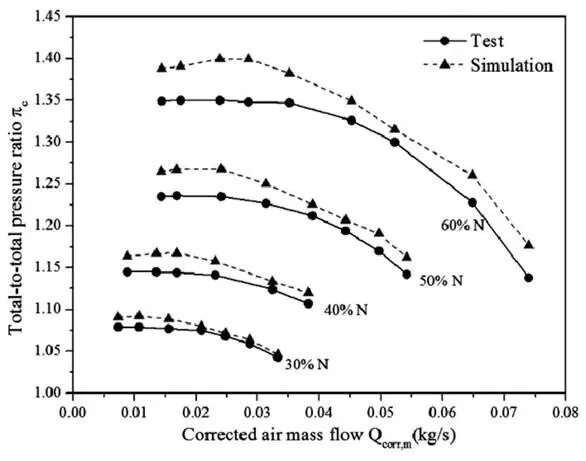
图3 叶轮仿真与试验特性曲线

由图3可知，仿真数据与试验数据基本吻合。而由于数值计算模型没有考虑壁面粗糙度，所以仿真数据较测试数据整体偏高。数值计算压比与试验数据较为接近，趋势基本一致，最大误差小于5%。因此，根据离心空压机测试环境监理的数值计算模型其计算精度在可接受的范围内。

1.3 优化过程

1.3.1优化目标

本次优化的目标是在满足空压机常用工况的压比基础上，提高空压机在常用工况的多变效率和。

由于多岛遗传算法为单一目标优化算法，因此需要把上述多目标优化问题转化为单目标优化问题。本文采用加权法将多目标归一化，通过为每个目标指定加权系数，加权系数表征了对多个目标的重视程度，通过这种方法使多个目标归一化为单个目标，后采用多岛遗传算法进行单目标优化，修改后的适应度函数如下：

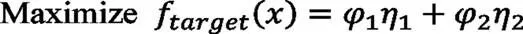
1，2分别为两个常用工况效率的权重，f()为优化目标。

1.3.2工况分析

要确定两个工况的权重，就必须对整体工况进行分析。本文选取NEDC典型工况来分析两个设计工况点的占比情况。

图4为对象车辆的NEDC工况图。本文将其常用工况划分为1-22kw与22k-46kw两个工况区间，如图所示。在分析了各个工况数据点在时间尺度上的占比后，得到功率分布如图5所示。可以看出，工况1的占比更大，与工况二的比值约为3.1，因此确定加权系数1=3.1，2=1。

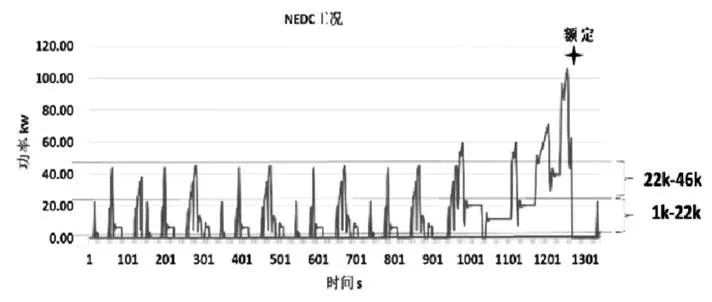
图4 NEDC循环工况

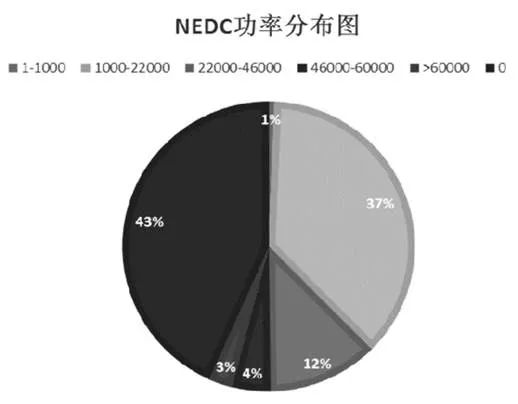
图5 功率分布图

本文针对燃料电池车用工况，确定空压机的两个常用工况点以及额定工况点的转速、压比和流量，对应工况如表2所示。

表1 各工况点对应流量、压比与转速

此外，空压机还应该满足各个转速下的喘振边界和阻塞边界的要求。针对各工况的喘振边界要求如表3。其中，在100000r/min大流量区域更易发生阻塞，考虑到计算资源，仅对这一转速提出阻塞要求。

表2 喘振和阻塞边界要求

1.3.3优化过程

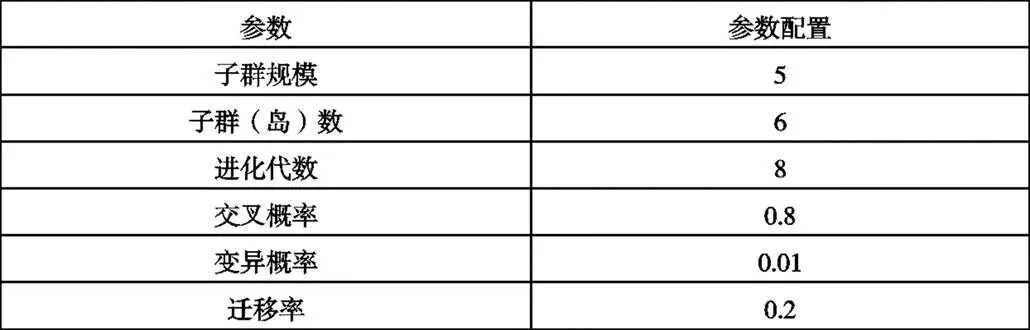
优化流程如图6，多岛遗传算法生成一组参数，然后用叶轮设计软件对叶轮造型；经过网格划分，采用数值仿真分析叶轮是否满足边界要求，如果不满足，则舍弃该组设计参数，再由多岛遗传算法进行下一次的迭代；如果满足边界要求，就对设计点进行仿真分析，记录该次计算结果。多岛遗传算法选择保留满足条件的优良基因，然后生成下一代的参数，重复以上过程直至达到遗传代数，输出最优结果。多岛遗传算法的参数设置如表4所示。

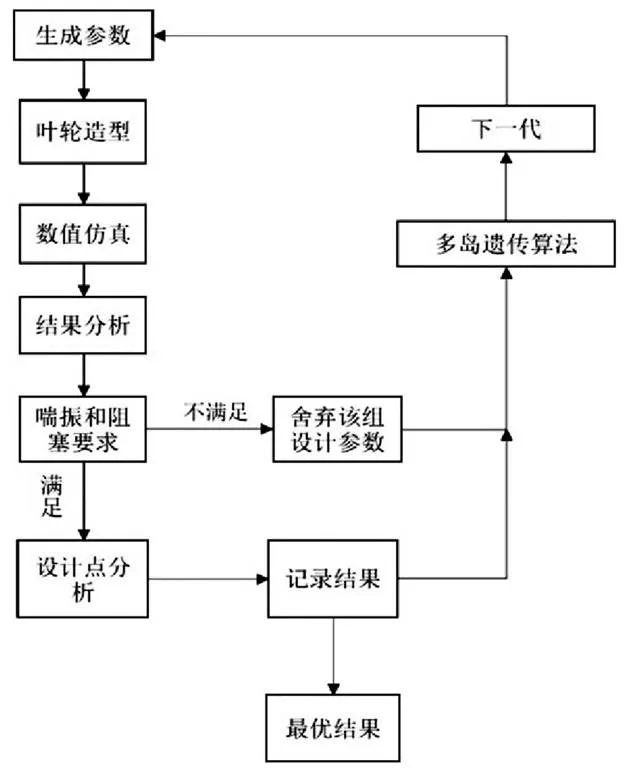
图6 算法运行流程

表3 多岛遗传算法参数设置

2 优化结果分析

经过优化，得到的最优结果参数与设计点效率分别如表5，表6所示：

表5 优化结果参数

表6 优化设计与原设计对比

从优化前后叶轮的压比与效率的对比结果可以看出，虽然使设计工况下的压比略有降低，但满足约束条件的要求，而各工况的效率分别提高3%，4%和1.4%，达到了优化目的。

进口安装角β1在轮毂和轮盖面均增大；进口轮盖直径D1s减小。进口的设计对于下游的流动有很大影响，若气流在进口处有明显的流场畸变，则主流区从一开始就具有明显的涡旋特征，且这种流场畸变不会在下游消失，甚至随着流动不断的发展加剧，以至于严重影响空压机性能。优化结果相较于原始设计，进口安装角度变大使得空压机在常用工况时气流更加均匀且无偏移的接近离心叶轮进口，即进口冲角损失更小，D1s不仅影响子午面的形状，也直接影响进口相对速度，叶轮流动损失与进口相对速度成正相关，减小进口轮盖直径有利于减小进口相对速度，进而减小了叶片进口段的流动损失。

出口安装角β2增大，出口直径D2和出口宽度B2均减小。对于后弯叶片，叶片出口角度β2越大，则做东能力越小，空压机的压比也就越小，但是出口角度的增大能够使气体出口绝对气流角减小，在小流量工况，出口绝对气流角的减小可以提高叶轮工作稳定性，有利于将喘振边界向小流量工况拓展。

出口宽度B2越小，叶轮的扩压度减小，并能够有效抑制气流分离，压缩机的稳定工作范围扩大，并且有利于小流量时气体的流动。但是，出口宽度的减小会使叶顶间隙对叶轮性能的影响增大，会导致较大的漏气损失。通过多岛遗传算法进行全局寻优，从而找到最优的B2值。

合适的轮径比Ds/D2既能够使叶轮充分利用离心力来提高压力，又不会引起内外壁面上速度的不均匀性，从而产生分离损失。优化后，轮径比Ds/D2没有明显变化，表明初始设计的叶轮进出口直径选择合理。

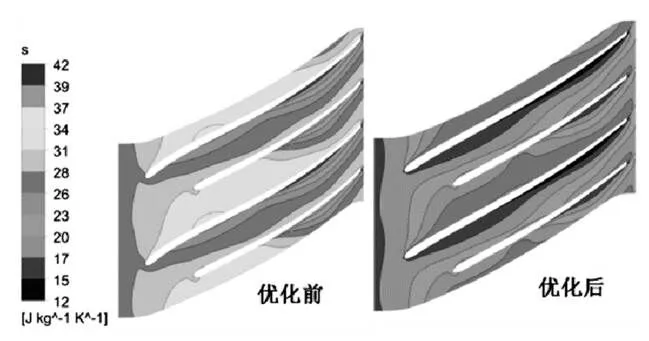
图7 工况一优化前后%50叶高处熵分布

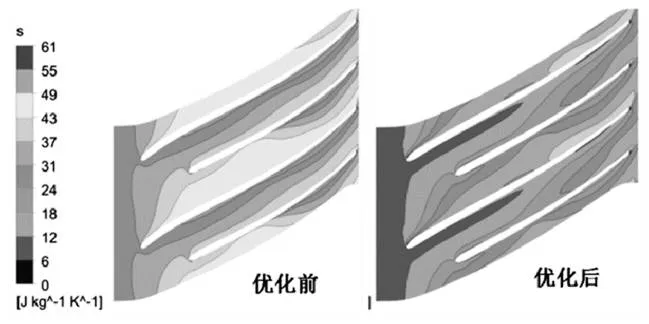
图8 工况二优化前后%50叶高处熵分布

熵可以用来解释优化前后效率变化的原因。熵和温度的改变对当地熵值以及整体压力或者动能损失等密切相关，可以通过对熵增云图的分析，确定损失位置及大小。图7图8给出了不同工况下50%叶高处的熵分布。可以看出，在两个设计工况点，优化后的叶轮在整个流道内的熵增都明显减少，其中，在主页片压力面最为明显，流动损失明显降低。这是由于叶轮参数的改变改善了流道内流体流动状况，同时，叶轮结构参数的改变也会引起叶轮型线的改变，优化后的型线更加符合流体在流道内的流动规律，使流动损失降低。

相对马赫数图可以表征流体在流道内的损失情况。图9 图10 为气体在50%叶高流道内的相对马赫数的变化。可以看出，在优化前，叶片的吸力面有低速涡团出现，它会影响流体在流道内的正常流动，可能导致流体回流等恶劣现象的出现，而优化后，流道内的低速涡团明显减小，且流道内的速度分布更加均匀，流体流动更加稳定，流道内流动损失降低。

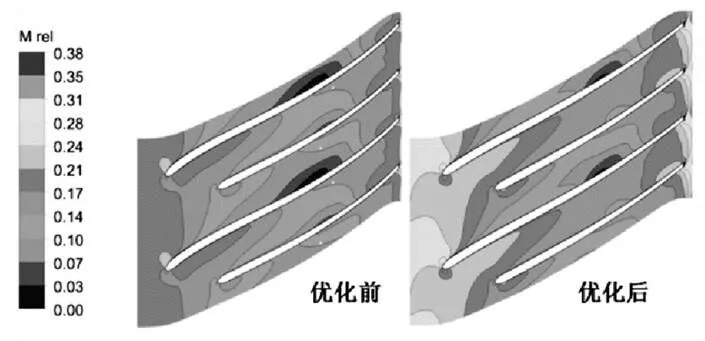
图9 工况一优化前后50%叶高处相对马赫数

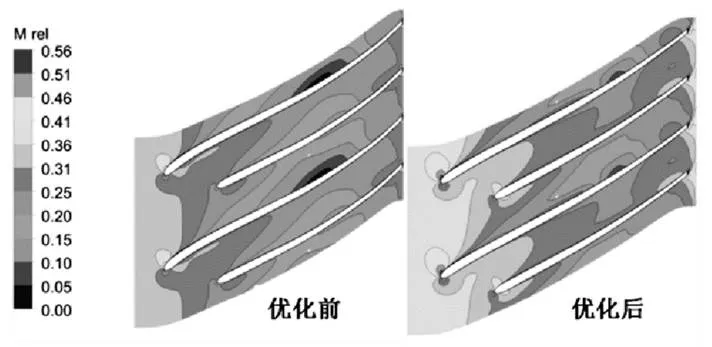
图10 工况二优化前后50%叶高处相对马赫数

为了进一步对比优化后叶轮与优化前叶轮性能，本文在设计点附近选取了另外四个工况点来对比其性能，结果如图11所示。其中case 1，case 2，case 3分别为三个工况，ori为初始设计，opt为优化设计。可以看出，优化后的空压机在设计转速下不同流量范围内的性能都有所提高，符合空压机经常在中低转速小流量区域运行的工作特点，达到了此次优化的优化目的，验证了本优化方法的有效性。

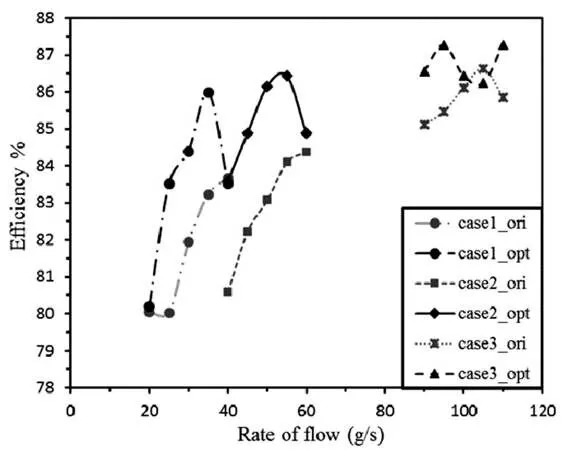
图11 多工况效率分布

3 结论

本文采用多岛遗传算法与数值仿真相结合的方法，针对燃料电池空压机常用工况，以工况点效率最优为目标，在空压机喘振边界和阻塞边界的约束下，对叶轮多个结构参数进行了优化。结论如下：

（1）通过对比常用工况下叶轮优化前后内部的熵和相对马赫数的分布，可以看出优化后叶轮内部的气体流动更加稳定，低速涡团和逆流区域减少，流道内损失降低。

（2）优化后，中低转速的小流量区域效率明显提高，更加符合车用燃料电池小流量区域的工作区间，使得空压机在整个车用工况的总体效率有所提高。

[1] 李建秋,方川,徐梁飞.燃料电池汽车研究现状及发展[J].汽车安全与节能学报,2014,5(01):17-29.

[2] 郭爱,李奇,陈维荣,等.车用燃料电池阴极系统特性[J].西南交通大学学报, 2013, 48(6):1052-1058.

[3] Engeda A. Effect of Impeller Exit Width Trimming on Compressor Performance[J].Proceedings of the Institution of Mechanical Engine -ers Part A Journal of Power & Energy, 2007, 228(8):878-888.

[4] Chiu Y J, Lien H C.A strategy of estimating fuel concentration in a direct liquid-feed fuel cell system[J]. Journal of Power Sources, 2006, 159(2):1162-1168.

[5] 汪创华,刘静,姚瑞锋,等.离心叶轮长,短叶片参数对压缩机性能影响分析[J].工程热物理学报,2013,34(02):270-273.

[6] 左曙光,韦开君,吴旭东,等.采用Kriging模型的离心压缩机叶轮多目标参数优化[J].农业工程学报,2016,32(02):77-83.

[7] 张良,许思传,万玉.PEM燃料电池用空压机多参数多目标优化[J].电源技术,2016,40(01):81-83+93.

[8] 王文杰,袁寿其,裴吉,等.基于Kriging模型和遗传算法的泵叶轮两工况水力优化设计[J].机械工程学报,2015,51(15):33-38.

[9] 周明,孙树栋.遗传算法原理及应用[M].国防工业出版社,1999:4.

[10] 丁泉惠,王森,黄修长,等.基于有限元法和多岛遗传算法的飞轮结构参数优化设计[J].噪声与振动控制,2016,36(02):56-6.

[11] 曾辉杰,燃料电池用压缩机叶轮参数对性能影响的研究[D],上海市曹安公路4800号:同济大学汽车学院,2014.03: 28-41.

Multi Parameter and Multi Conditions Optimization of Centrifugal Compressor Impeller for Fuel Cell Vehicles*

Zhao Qing, Zhang Yuemeng, Xu Sichuan

( School of Automotive Studies, Tongji University, Shanghai 201804 )

The consumption of centrifugal air compressor accounts for about 20% of the output power of fuel cell. In order to improve the fuel cell efficiency in the whole vehicle working condition, this paper combines multi-island genetic algorithm with numerical simulation, and proposes a multi-condition and multi-parameter optimization method for centrifugal air compressor. In this paper, based on the NEDC working condition, the pressure ratio under each working condition and the surge and blocking boundary of the compressor are taken as the constraints. Seven key parameters including the inlet blade tip installation angle, the inlet blade bottom installation angle, the inlet blade diameter, the outlet width, the outlet diameter, the outlet installation angle and the diffuser length are selected as an optimization variable to optimize the efficiency of each working condition. Compared with the original design scheme, the flow in the impeller passage is more stable after optimization. The low-speed vortex group and counter-current area are obviously reduced, and the loss is reduced and the efficiency of the two working conditions is increased by 3% and 4% respectively.

Fuel cell; Centrifugal air compressor; Multi working conditions and multiple objectives; Multi island genetic algorithm

A

1671-7988(2018)24-25-05

U469

A

1671-7988(2018)24-25-05

U469

展庆（1992.11-），男，同济大学动力机械与工程硕士学位。研究方向：燃料电池空气供应系统的设计与优化。

许思传（1963.01-），男，吉林工业大学机械与工程专业博士学位，现为同济大学汽车学院教授。研究方向：燃料电池发动机系统、整车热管理。课题来源于项目：高比功率燃料电池发动机关键技术研究与平台开发（2017YFB0102802）。

10.16638/j.cnki.1671-7988.2018.24.008