结合稳态卡尔曼滤波的永磁同步电机滑模观测器

莫丽琴

(江苏海事职业技术学院，南京211170)

0 引言

随着稀土材料和功率电子的发展，永磁同步电机(以下简称PMSM)近年来在工业机器人、电动汽车等新兴领域获得了广泛的应用［1］。相比于异步电机，PMSM的功率密度更大、效率更高，而且少了转差之后控制也更加简单。

PMSM的矢量控制需要获得准确的转子位置，而机械位置传感器存在造价高以及在恶劣环境中无法使用的问题，因此越来越多的学者研究了无位置传感器控制，采用PMSM的电压和电流对转子位置进行估计。无位置传感器算法可以分为两类［2－4］，即基频反电动势类和高频注入类。由于高频注入算法会引入噪声和损耗，因此实际使用中应用广泛的还是基频反电势类算法，包括滑模观测器、卡尔曼滤波器和模型参考自适应算法等。其中，滑模观测器由于鲁棒性好、响应快和算法简单而特别备受关注［5－6］。

滑模观测器将定子电流和电压信号作为输入，实时观测反电动势信息，进而得到转子位置。但传统滑模观测器由于滑模面的切换而存在高频抖振，会在反电动势中引入高频噪声，普通的低通滤波器也难以完全滤除反电动势信息中的高频噪声，严重影响了观测器的精度。对此，有学者采用了锁相环(以下简称PLL)技术来抑制噪声［7］。将滑模观测器估计到的反电动势作为PLL的输入，利用PLL的低通滤波特性和跟踪特性，完成转子位置的准确快速跟踪。在此基础上，为了提高PLL的性能，文献［8］采用改进的分数阶PLL，采用分数阶PI代替了PLL中的传统PI，从而在动态上获得了比传统PLL更好的跟踪性能，但分数阶PI的实现较困难。

本文针对PMSM的滑模观测器抖振问题，采用了稳态卡尔曼滤波器(以下简称SSEKF)来抑制高频噪声。SSEKF是将EKF算法中的卡尔曼增益矩阵视为常数，从而极大地简化了滤波器的形式［9］，在运算量很小的同时，能达到比PLL更好的性能。实验结果表明，SSEKF能够有效减小滑模观测器的位置估计误差。

1 PMSM滑模观测器

滑模观测器是一种变结构的设计，通过设计合理的滑模切换函数，使得观测误差沿着滑模面变化，最后收敛到零。本文将PMSM的定子电压和电流作为观测器的输入，用于观测反电动势信息。首先考虑PMSM在两相静止坐标系下的数学模型:

式中:uα，uβ，iα，iβ分别是 α，β 轴的定子电压、定子电流，Ls是定子电感;Rs是定子电阻;ω是转子转速;ψf是永磁体磁链。

当获得α，β轴的反电动势后，可以计算得到转子位置:

根据滑模理论，以观测电流与实际电流的误差构建滑模切换函数:

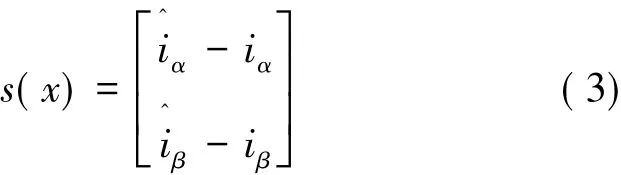
采用符号函数sign(x)构建滑模观测器:

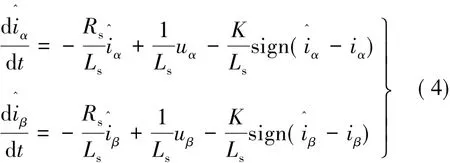
由式(2)和式(4)得到电流误差方程:

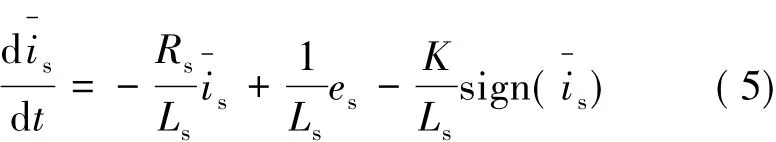
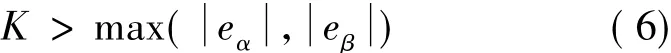
当滑模增益K满足式(6)条件时，式(4)能够准确估计出反电动势的值。通常情况下，K取值较大才能满足条件，因此观测器会有很大的抖振噪声。为此，采用低通滤波器对观测值进行滤波，得到连续的反电动势信息。为了减小低通滤波器引起的相位滞后，其截止频率较高。

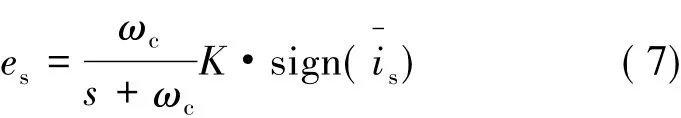
考虑到由式(4)得到的反电动势信息中高频噪声较大，低通滤波器也难以将其完全滤除，因此有学者将滑模观测器和PLL结合起来，利用PLL的跟踪特性和滤波特性获得更准确的转子位置信息，其框图如图1所示。

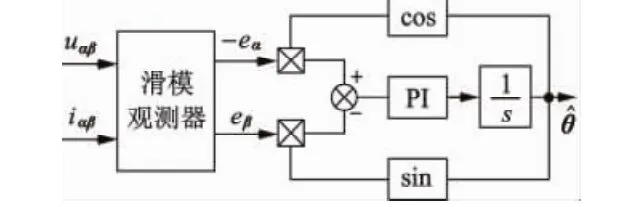
图1 结合PLL的PMSM滑模观测器

PLL在稳态时有较好的滤波效果，能够有效消除滑模观测器的高频抖振。但是由于PI参数的限制，PLL的带宽较小，因此动态性能较差，在转速变化时会产生较大的估计误差。对此，本文采用稳态卡尔曼滤波器SSEKF来代替PLL。

2 稳态卡尔曼滤波器

考虑如下的电机运动模型:

式中:T是采样周期;θk是转子位置;ωk是转子转速;wk是零均值的白噪声。可以看到，式(9)将电机运动形式看成加速度是恒定的。

将滑模观测到的反电动势作为观测相量，即:

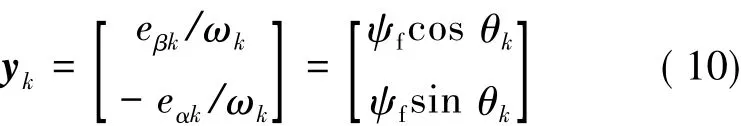
将状态相量选择xk=［θkωkak］T，就能获得如下的状态空间方程:

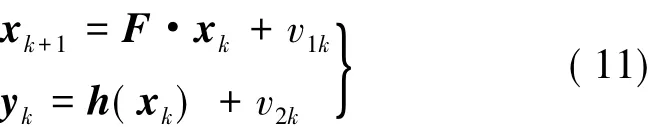
在建立状态空间模型之后，状态相量xk就可以由下面的递推公式得到:

式中:R1和R2分别是模型误差和观测误差，Hk是h的一阶近似，即:

经过式(17)的变换，所有的Hk变成了常数矩阵H，从而Pk+1也成为了时不变的，最终Pk会收敛到一个稳态矩阵 P－，P－可以由Riccati方程求得。此时，卡尔曼增益Kk虽然是时变的，但可以由以下计算得到:

式中:k1，k2，k3是常数。

从而，对于式(15)，有:

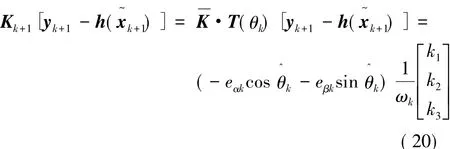
将式(20)代入到式(15)中，就可以获得如下的SSEKF递推公式:

式(21)的SSEKF算法形式简便，计算量小，容易实现，但是动态性能却优于PLL。结合了SSEKF的PMSM滑模观测器框图如2所示。

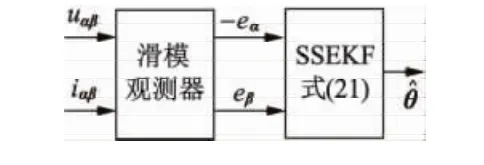
图2 结合SSEKF的PMSM滑模观测器

3 仿真和实验验证

3．1 SSEKF和PLL的仿真对比

本文在滑模观测器的基础上，结合了SSEKF算法用于高频抖振的抑制。为了表明SSEKF相对于PLL的优越性，本文首先进行仿真验证。

仿真中，电机处于加速状态，其运行频率从10 Hz逐渐增大到40 Hz，此时反电动势也随着转速升高而增大。利用PLL和SSEKF分别解算出转子位置，其仿真结果如图3所示。

PLL 的参数设置为kp=0.2，ki=0．02;SSEKF 的参数设置为 k1=0．2，k2=0．02，k3=0．006。可以看到，当反电动势信息中包含有高频噪声时(信噪比SNR=34 dB)，直接用式(8)的arctan函数计算得到的转子位置中也包含了高频误差，其误差峰峰值约为4°。若采用PLL对反电动势波形进行处理，则转子位置结果的误差会减小，但是在加速过程中会出现估计位置偏离真实位置的情况，PLL的转子位置估计误差能达到3°。同时，PLL的转速估计误差也达到了80 r/min。当采用SSEKF处理反电动势信息时，不会出现由于速度变化产生的动态误差，同时高频误差峰峰值减小到2°，SSEKF的转速估计误差也一直在零附近波动，误差约为5 r/min。仿真结果表明，SSEKF能有效削弱高频抖振带来的误差，同时能够保证不会产生动态误差。

图3 SSEKF和PLL对比仿真结果

3．2 SSEKF 实验结果

为了验证本文结合SSEKF的PMSM滑模观测器的性能和优越性，在一台两对极隐极型SPMSM上进行了实验，实验平台如图4所示。电机的参数如表1所示。

图4 实验平台

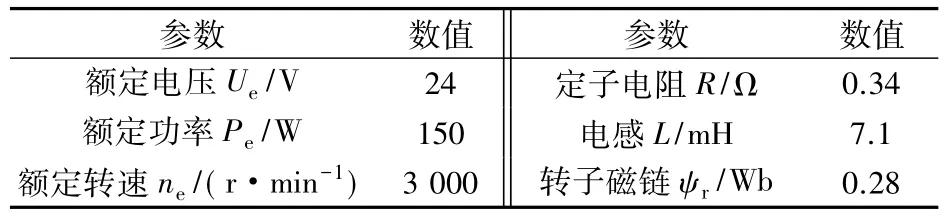
表1 实验用PMSM电气参数

如图5所示，使用滑模观测器观测到的转子位置作为反馈，进行PMSM的调速控制，负载转矩维持在0．15 N·m不变，转速从1500 r/min升到3 000 r/min再降到1500 r/min，编码器的信号仅用于比较而非闭环反馈。由图5可以看到，在此过程中，使用结合SSEKF的滑模观测器位置估计误差控制在10°以内，即使在高速段误差也维持在15°以内，此时的转速误差约为80 r/min。而如果采用传统的滑模观测器，则误差达到25°，在高速段误差则更大。因此，实验结果表明，采用本文的改进滑模观测器能够实现PMSM的调速控制，且其观测性能要优于传统滑模观测器。

图5 实验结果

4 结语

针对PMSM的无传感器控制，本文研究了一种结合稳态卡尔曼滤波的滑模观测器。在传统滑模观测器的基础上，利用SSEKF对反电动势信息进行滤波处理，从而有效削弱了滑模观测器的抖振噪声。由于SSEKF将增益矩阵视为常数，因此具有简洁的表达形式，便于工程实现。仿真结果表明，在调速过程中SSEKF具有比PLL更小的动态误差。最终的实验结果也表明，本文的结合SSEKF的滑模观测器能够更准确地获得转子位置，能够完成PMSM的无传感器调速，由此验证了算法的可行性和有效性。