基于MUSIC与SVRM的感应电动机转子断条故障检测

刘志坚，李德路，吴 玮

(江苏建筑职业技术学院，徐州221116)

0 引 言

感应电动机作为工农业生产的重要动力设备，对其进行可靠的状态监测和故障诊断颇为重要［1－2］。转子断条故障是电机常见故障之一，它不仅会导致生产受到不良影响，降低产品质量，还可能产生危及设备以及人员安全的事故［3］。因此，感应电动机转子断条故障检测一直以来都是研究的热点。

基于电机定子电流特性分析(以下简称MCSA)是感应电机转子断条故障诊断的常用方法［4］。快速傅里叶变换(以下简称FFT)是最常用的电流特性分析方法。MCSA方法通过检测感应电动机定子电流中断条故障特征频率(1±2s)f1来判断电机是否存在故障［5］。轻载时特征频率(1±2s)f1与基频f1极其接近，传统的MCSA方法是通过增加采样信号长度来保证特征频率(1±2s)f1的检测精度。但是该方法不可避免会受到负载波动和噪声的干扰，由此引发频谱泄露等问题，从而导致传统方法精度不高［6］。

基于此，频谱估计被引入到电机故障检测中［8］。多重信号分类(以下简称MUSIC)是一种常见信号频谱分析方法，其基于谱估计技术，对数据长度要求不高，即使在较短的数据量情况下也具有较好的检测精度和较高的频率分辨力。因此，将MUSIC引入到电机故障诊断中可以避免传统方法因负载波动致使检测精度不高的缺点。然而MUSIC不可以获取特征信号的初相角以及幅值，只能检测出信号频率的大小。为此许多学者将优化算法PSA［9］、SAA［10］、PSO［11］等与 MUSIC 相结合用于获取信号的幅值和相位信息。文献［12－13］提出了一种迭代变权最小二乘支持向量机的电力系统谐波检测方法，但该方法只能检测幅值和相位角，而对于频率的测量却只能通过“试探”的方法获得，从而大大降低了算法的计算速度。文献［12］将Root－MUSIC和SVRM相结合，成功用于间谐波参数估计。文献［13］将TLS－ESPRIT与SVRM相结合，对间谐波进行了精确检测［15］。

为此，针对MUSIC不能估计信号频率，且感应电机故障诊断时因负载波动、噪声等对检测精度的影响等问题，本文将MUSIC和支持向量回归机(以下简称SVRM)相结合用于感应电动机转子断条故障检测。首先以转子断条故障仿真信号对本文方法在数据量、抗噪能力、计算精度等方面的性能进行分析，然后基于Y132M－4型感应电动机进行实验，并通过实验结果证明了理论分析的正确性。

1 MUSIC算法

MUSIC 算法的基本原理［14－15］:

用含有p个频率成分的组合表示采样信号［1，6］:

式中:p表示谐波个数;fi表示第i次谐波频率;Ai表示第i次谐波幅值;φi表示第i次谐波初始相位角;N表示采样点数;w(n)表示白噪声，白噪声方差取σ2，均值取 0。

设置一个m×N阶矩阵，为确保m≥p，通常使m=3N/4。

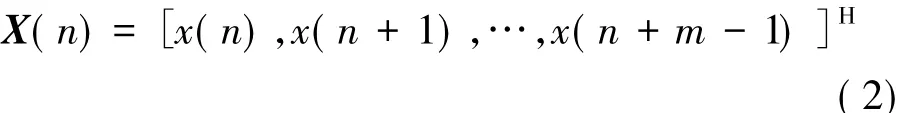
则X(n)的自相关矩阵:

式中:H表示共轭转置;E表示数学期望。

接着，对自相关矩阵进行特征值分解，并降序排列特征值，确定前p个为主特征值，主特征值对应特征向量构成的空间为信号子空间S;后m－p个为次特征值σ2，其特征向量构成的空间为噪声子空间V。

然后，便可以构造频谱估计表达式:

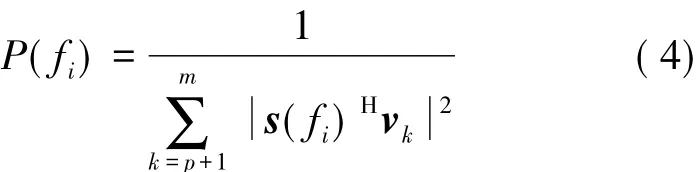
式中:s(fi)=［1，ej2πfi，…，ej2π(N－1)fi］H。

最后，取fi=iΔf，计算 P(fi)。由运算结果找出最大的p个峰值对应的频率f1，f2，…，fp，即为所求。Δf为频率分辨率，本文取 0．01Hz。

由此可知，MUSIC可以通过设置不同的分辨率Δf，确定信号频率估计的精度，但是不能求得相应频率成分的幅值和相位角。

2 SVRM

SVRM是基于非线性变换，将输入空间变换至高维空间，接着在此高维空间中线性回归，进而逼近原函数［17－18］。

设{xi，yi}(i=1，2，…，n)为原始采样信号，构造线性回归函数f(x)=wx+b，并用其去拟合{xi，yi}。

设拟合的误差精度为ε，则有下式［12］:

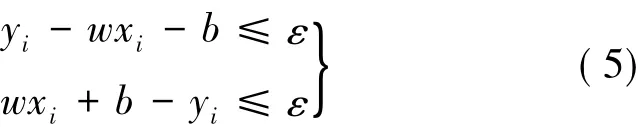
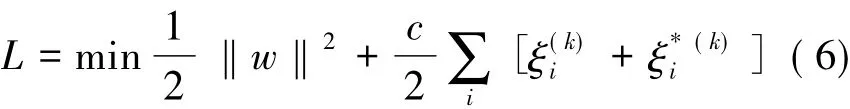
约束条件:

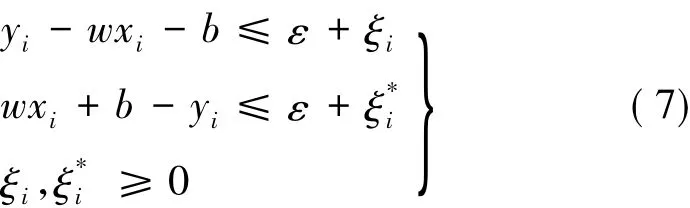
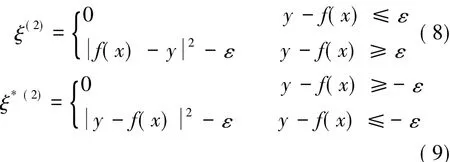
对于p个频率成分的电力系统信号的离散时间序列{xi，yi}可用如下形式表示:

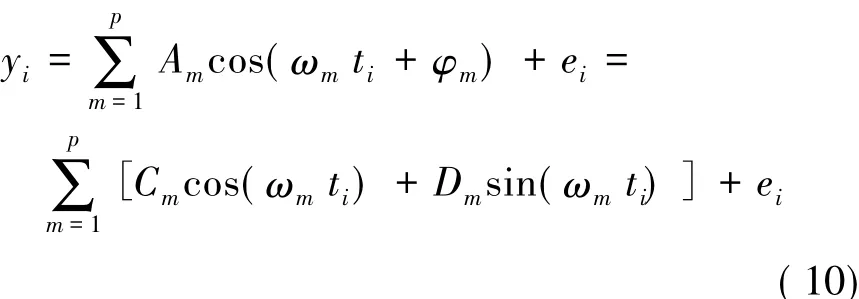
式中:Am，φm为频率ωm所对应的幅值和相位;ei为ti时刻模型的误差。Cm=Amcos φm;Dm=Amsin φm。

则式(6)、式(7)变为式(11)、式(12):

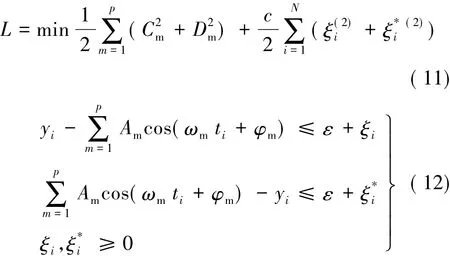
根据拉格朗日函数，式(11)、式(12)可变为:

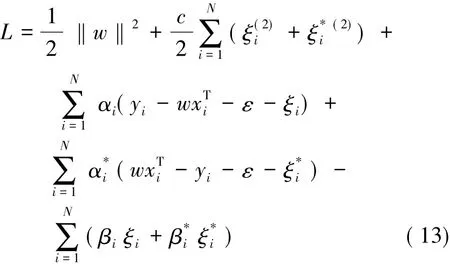
式中:αi为拉格朗日乘子。作如下假设:

那么，式(13)可以变为:

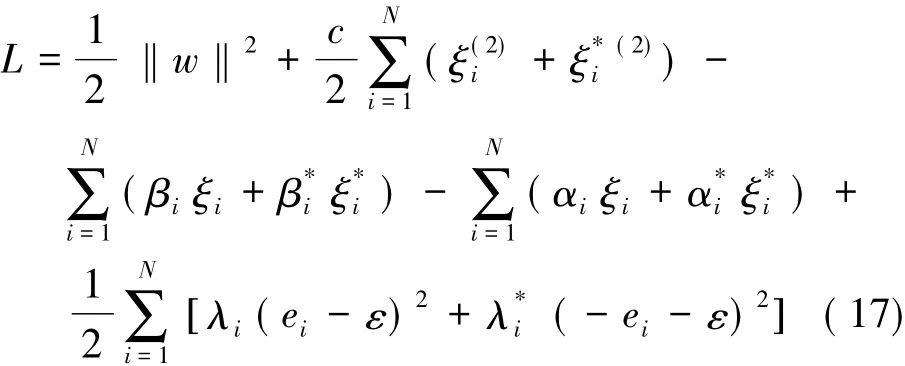
拉格朗日乘子和ei的关系可以通过式(7)、式(8)以及式(13)推出，为下式:

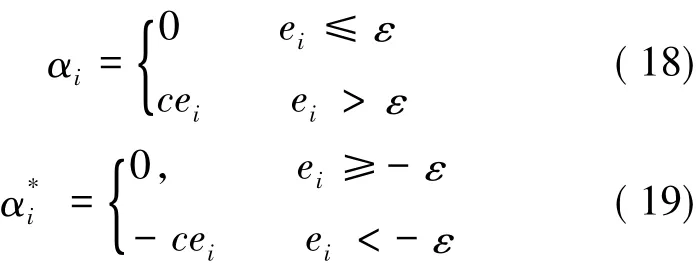
式中:

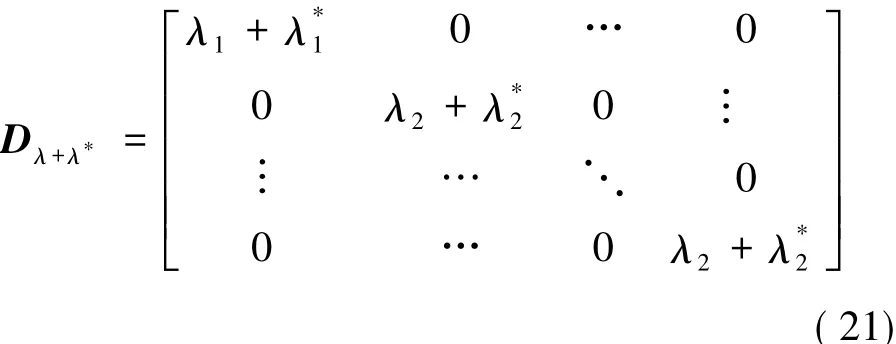
Dλ－λ*与 Dλ+λ*类似。

综上所述，SVRM方法步骤可归纳如下:

(1)随机赋予w一组初始值，并令r=0;

(2) 计算ei=yi－wxTi;

(3)根据式(18)、式(19)求解拉格朗日乘子;

(4) 根据式(15)、式(16)求λi

(5)根据式(20)计算wr+1;

(6)r=r+1，直到达到最大迭代次数为止。

通过以上分析，由式(14)及步骤(2)可知，在构造信号表达式时，w是待求量，而其中的xi和频率有关且未知。因此本文引入MUSIC方法事先确定信号的频率，从而提高SVRM的计算精度和计算速度。

3 感应电动机断条故障检测的新方法

基于MUSIC与SVRM的感应电动机转子断条故障检测方法一共分为两步:第一步，根据采样获得的定子电流信号，采用MUSIC对其频率成分进行估计;第二步，在频率已知的基础上，利用SVRM对相应频率的幅值和相位角进行估计。

3．1 基于断条故障模拟信号的算法性能分析

感应电动机转子断条故障时，其定子电流信号可以采用如下模拟形式:

首先，采用MUSIC计算该信号的频率，取频率分辨率为0．01Hz，其结果如图1所示。

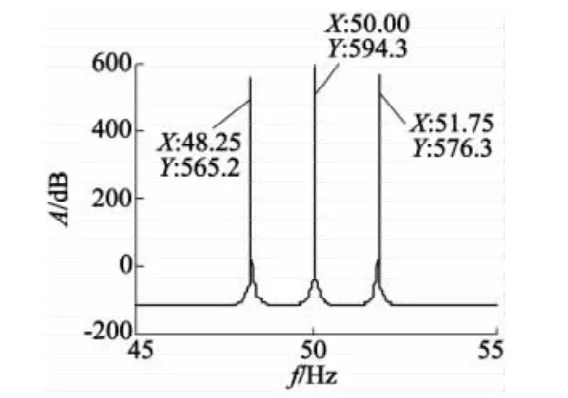
图1 定子电流MUSIC频谱

模拟信号中各个参数设置如下:基频信号的频率为50 Hz，幅值为 10 A，相位角为0．214 8 rad;左边频分量的频率为48．25 Hz，幅值为 0．1A，相位角为0．3214 rad;右边频分量的频率为 51．75 Hz，幅值为0．05 A，相位角为0．1312 rad。信号采样频率为 300 Hz，采样点数为600。

由图1可知，MUSIC可以准确估计出短时采样数据的频率，但是对于计算出的幅值却没有意义。

然后，利用SVRM计算该信号相应频率成分的幅值和相位角，结果为:基频幅值和相位角分别为9．993 A和0．214 8 rad，左边频的幅值和相位角分别为0．100 0 A 和 0．322 0 rad，右边频的幅值和相位角分别为0．050 0 A和0．130 0 rad。SVRM参数设置为ε=0，c=25(全文均为此参数)。由此可见，SVRM对信号的幅值和频率具有较高的估计精度。

本文通过对模拟信号中加入不同信噪比的高斯白噪声来检验本文方法的抗噪能力，可作出如图2所示的相对误差曲线。

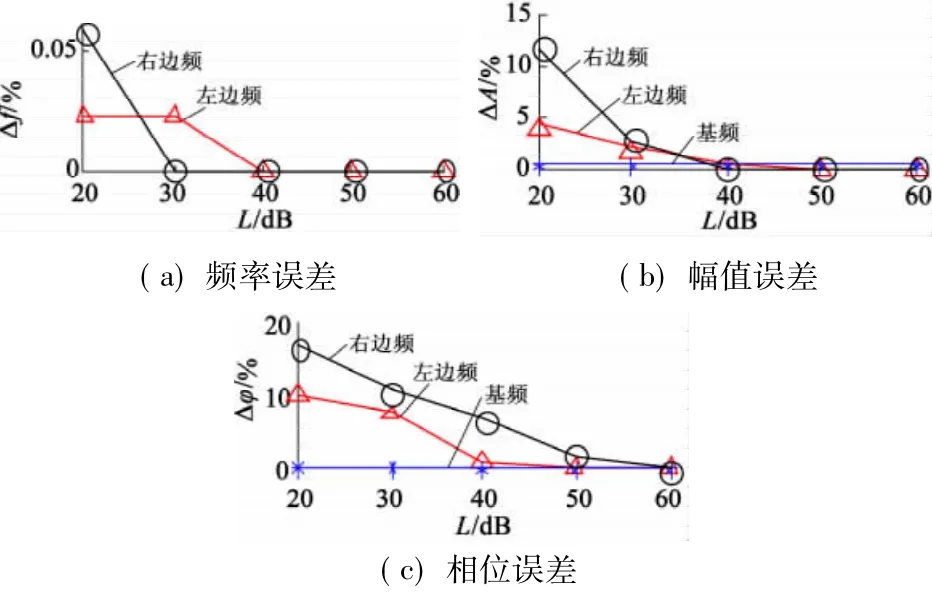
图2 不同信噪比高斯白噪声下的相对误差曲线

在不同信噪比下MUSIC运算得到的基波频率均为50 Hz，因此在图2的频率误差图中并没有画出其误差曲线。由图2可知，MUSIC对信号的频率具有较好的估计结果，即使在强噪声、短数据情况下仍具有较高的精度。而SVRM在对信号的幅值和相位角进行估计时，不仅受到噪声的影响，同时还会受到MUSIC对相应频率大小估计精度的影响，频率估计愈准确，幅值和相位角估计也愈准确。但在短数据和强噪声下，SVRM对信号的幅值仍然具有较高的估计精度。虽然对于相位角估计结果误差相对较大，但感应电动机转子断条故障程度的判断通常是求取定子电流特征分量幅值和基波幅值之比，暂时未用到各频率成分的相位角。因此，基于MUSIC和SVRM的感应电动机转子断条故障检测方法具有较强的抗噪能力和避免负荷波动干扰的能力。

3．2 实验研究

本文通过Y132M－4型感应电机进行实验研究，电机参数如表1所示。

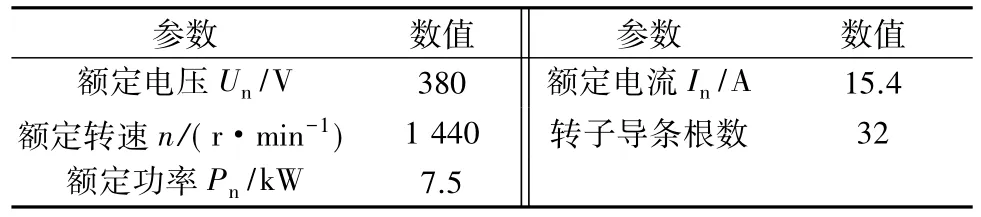
表1 Y132M－4型感应电机参数表

实验时采样频率为5 kHz，其计算结果如表2所示。为了便于比较，同时采用FFT方法对定子电流进行分析，其中采用本文方法时的数据采样点数为10 000，FFT的数据点数为20 000。

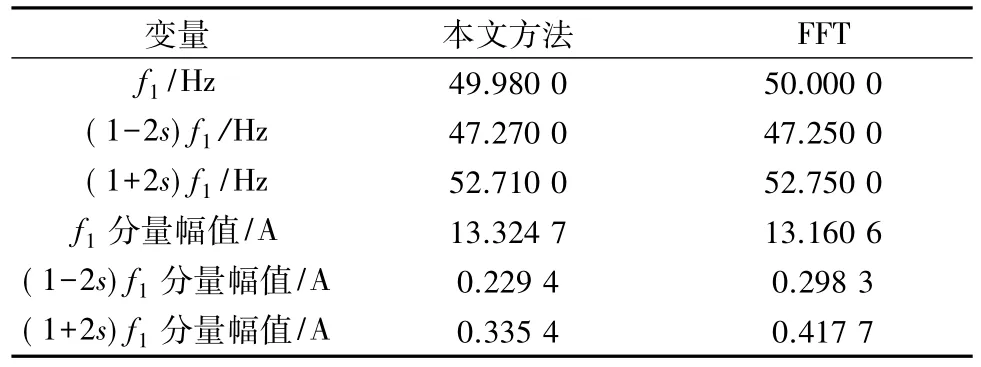
表2 转子断条实验结果

由表2可知，采用本文方法用于感应电动机转子断条故障检测时，具有较好的精度。如果进一步提高MUSIC算法的搜索步长，频率估计结果会有更高的精度，这又会进一步提高SVRM的计算精度，可以有效避免以FFT为基础的定子电流频谱分析方法的频谱泄露问题，同时可以减轻基频分量淹没边频分量的影响。

图3为转子1根断条时定子电流信号波形。

图3 定子电流信号波形

4 结语

本文研究了一种基于MUSIC与SVRM的感应电动机转子断条故障检测方法，并进行了性能分析与实验研究，得出如下结论:

1)本方法克服了传统FFT方法的频谱泄露等问题，同时解决了MUSIC不能计算信号幅值和相位角的问题;

2)本方法在进行断条故障检测时，在保证一定精度的前提下所需数据量少，从而可以避免因负荷波动对检测结果的不良影响问题;

3)由于本方法具有较好的抗噪能力，因而更加适用于工程实际，具有一定的应用前景。