饱和砂土地基应力扩散效应的离心模型试验研究

董晓朋, 马建林, 胡中波,2, 李军堂, 徐 力

(1.西南交通大学土木工程学院,成都 610031； 2.中国长江三峡集团,北京 100038； 3.中铁大桥局集团有限公司,武汉 430050； 4.中铁大桥勘测设计院集团有限公司,武汉 430056)

饱和砂土地基应力扩散效应的离心模型试验研究

董晓朋1, 马建林1, 胡中波1,2, 李军堂3, 徐 力4

(1.西南交通大学土木工程学院,成都 610031； 2.中国长江三峡集团,北京 100038； 3.中铁大桥局集团有限公司,武汉 430050； 4.中铁大桥勘测设计院集团有限公司,武汉 430056)

沉井基础在大跨度桥梁工程中的应用已越来越广泛。在沉井基础的沉降计算中,附加应力影响范围的确定一直是重点和难点,主要涉及应力扩散起始位置、扩散角大小和附加应力影响深度3个方面。针对目前现有理论及常用规范对确定附加应力影响范围的不适用性,开展沉井基础作用下饱和砂土应力扩散效应的研究具有十分重要的意义。通过离心模型试验开展4组不同埋置深度条件下沉井基础的静载荷试验,确定饱和砂土地基中附加应力的影响范围,试验结果可为工程设计提供依据。

离心模型试验；应力扩散；沉井基础；沉降计算；饱和砂土

近年来，伴随着我国高速交通的快速发展，一大批跨江越海大桥得以建造。沉井基础以其承载能力大、刚度大、协调不均匀沉降的能力强、抗震性能好等优点已被广泛应用于工程实践[1-3]。

目前，我国工程界通常采用分层总和法计算地基沉降[4]。对于沉井基础的沉降计算而言，国内外现行计算方法往往将其视为一个深埋的实体基础，应用浅基础的沉降计算方法进行沉降计算，由于基础埋深较深、上部结构与地基基础共同作用及侧向约束作用，其沉降计算方法更加复杂，至今还未完全解决[5]。为了考虑土的压缩性对基础沉降的影响，首先需要确定附加应力的影响范围，其涉及地基类型，基础形式、埋深，外部荷载等多个因素的影响，主要包括应力扩散起始位置、扩散角大小及附加应力影响深度3个方面。

在确定应力扩散起始位置及扩散角大小时，主要有3类方法：一是考虑从承台开始的应力扩散角α=φ/4(φ为土体的内摩擦角)，附加应力从基底平面算起[6]。二是附加应力从基底平面算起，不考虑应力扩散角，国内现行规范[7-11]均采用此法。三是应力在基底以上某一高度(1/m)处开始扩散，太沙基和皮克[12]曾建议1/m=1/3，附加应力也在该位置起算；美国桥梁设计规范[13]沿用此法，且1/m的值常取1/3或1/2。

对于附加应力影响深度的计算，现行常用规范多采用“应变控制法”或“应力控制法”确定。其中，铁路规范[7]、公路规范[8]和建筑地基规范[9]均采用“应变控制法”来确定，所不同的是，上述各规范对计算深度以上所取土层厚度的规定有所不同，根据该薄层所产生的沉降量不大于修正前总沉降量的0.025倍，以此来确定影响深度，因此3种规范方法得到的影响深度各不相同[14]。桩基规范[10]则采用“应力控制法”满足计算深度处的附加应力为该处自重应力的0.2倍来确定；上海地基基础设计规范[11]要求计算深度处的附加应力为该处自重应力的0.1倍；美国桥梁设计规范[13]规定计算深度处的附加应力为基底附加应力的0.1倍，以此来确定影响深度。此外，当无相邻荷载影响且基础宽度在1～30 m时，附加应力影响深度可近似由zn=b(2.5-0.4lnb)进行计算[9]。

上述理论及规范虽给出了附加应力影响范围，但由于计算模式和设计人员技术经验不同，往往选用的方法不同，最终导致沉降计算结果的差异，从而增加了工程设计计算的盲目性和风险。鉴于此，基于离心模型试验，开展了饱和砂土地基中沉井基础的静载荷试验，确定了附加应力的影响范围，对实际工程有一定的指导意义。

1 试验方案

1.1 试验设备及装置

本试验采用西南交通大学TLJ-2型土工离心机，其最大容量为100 gt，最大加速度为200g，有效半径为2.7 m。

试验采用的模型箱正面为有机玻璃板，其余三面及底板为钢板，尺寸为80 cm(长)×70 cm(宽)×70 cm(高)，模型试验布置如图1所示。模型试验的边界效应主要来自模型箱边壁对模型的约束作用。当模型中结构物与侧壁相对较近时，模型箱的约束会明显影响到结构物的性状[15]。本试验沉井基础的尺寸为10 cm(长)×7.5 cm(宽)，与箱壁最小距离大于4B(B为基础宽度)，沉井基底与箱底最小距离为4B，可忽略边界效应[16]。

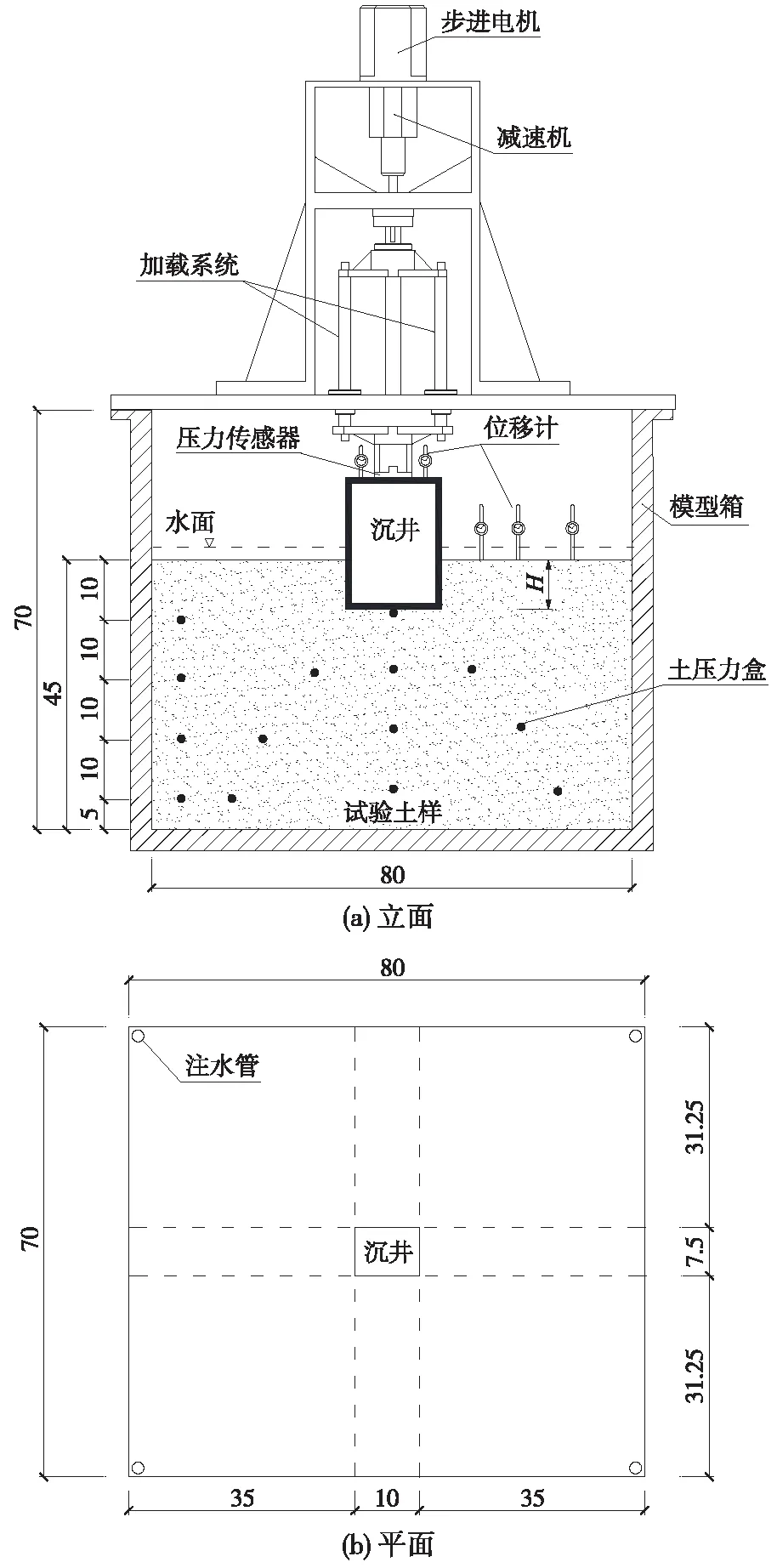
图1 试验布置示意(单位：cm)

1.2 地基土的制备与物理力学特性

试验土样选用福建标准砂，按每层厚度为5 cm分层摊铺砂土地基，使用压实仪进行多遍夯击，并根据每层的体积计算出每层砂土质量。重复此步骤，直至地基厚度达到设计要求的45 cm。完成试验土样的填筑后，通过预先埋设在模型箱四角的注水管缓慢从箱底向上注水，当水面高于土面1 cm时，终止注水，静置24 h，使砂土在自重作用下压密，以保证每次试验土样的均一性。试验土样的参数见表1。

表1 模型试验福建标准砂基本参数

注：内摩擦角、黏聚力均由直接剪切试验测得。

1.3 试验加载及量测

本试验采用西南交通大学胡中波等人设计的加载系统对沉井施加竖向荷载，如图1所示。试验采用分级加载，每级加载量为0.2 kN，加载完后实时观察测力传感器读数的大小，待读数稳定后，记录读数并施加下一级荷载，直至加载至某级荷载时，测力传感器读数不能稳定或小于上一级稳定荷载，停止加载，终止试验。

本试验采用的土压力传感器为TY102型土压力盒，位移传感器为CW50型差动式位移传感器，其外形如图2所示。

图2 传感器

1.4 试验安排

针对饱和砂土地基开展了4组模型试验，具体试验安排见表2。

表2 试验安排

试验假定应力线性扩散，传感器布置如图3～图6所示。

图3 传感器布置(H=0cm)(单位：cm)

当基础埋深H=0 cm时，应力从基底开始扩散。根据图3中传感器与虚线的相对位置，将试验土样分为4个区，由左到右分别为Ⅰ区、Ⅱ区、Ⅲ区、Ⅳ区。Ⅰ区传感器位于同一竖直断面上，且远离沉井基础，用于判定同一水平断面其他位置处是否产生附加应力；Ⅱ区靠近土样表面的两支传感器考虑23°(2φ/3，φ为试验土样的内摩擦角)的扩散角布置，靠近模型箱底的3支传感器考虑29°(5φ/6)的扩散角布置；Ⅲ区传感器位于同一竖直断面上(基底以下中心位置)，用于判定附加应力影响深度；Ⅳ区靠近土样表面的2支传感器考虑35°(φ)的扩散角布置，靠近箱底的3支传感器考虑40°的扩散角布置。

图4 传感器布置(H=15 cm)(单位：cm)

当基础埋深H=15 cm时，试验土样分区同前所述。参照美国桥梁设计规范，Ⅱ区应力从基底以上H/3位置开始扩散，参考H=0 cm的试验结果，考虑32°的扩散角布置传感器。Ⅳ区应力从基底以上H/2位置开始扩散，同样考虑32°的扩散角布置传感器。

图5 传感器布置(H=5 cm)(单位：cm)

当基础埋深H=5 cm时，试验土样分区同前所述。参考H=15 cm的试验结果，应力从基底以上H/3位置开始扩散，Ⅱ区考虑33°的扩散角布置传感器，Ⅳ区考虑34°的扩散角布置传感器。

图6 传感器布置(H=10 cm)(单位：cm)

当基础埋深H=10 cm时，试验土样分区同前所述。参考H=5 cm的试验结果，应力从基底以上H/3位置开始扩散，Ⅱ区考虑34°的扩散角布置传感器，Ⅳ区考虑35°的扩散角布置传感器。

2 试验结果

2.1 应力扩散起始位置及扩散角大小

对于任一水平断面的传感器，由于Ⅰ区传感器距离基础较远，不受附加应力影响，其读数为上覆土压力值，可通过比较Ⅰ区和Ⅱ区、Ⅳ区应力的大小判定Ⅱ区、Ⅳ区是否受附加应力影响，当Ⅱ区、Ⅳ区应力值与Ⅰ区接近时，可近似认为该位置不受附加应力影响；当Ⅱ区、Ⅳ区应力值大于Ⅰ区时，则该位置受到附加应力影响。

根据上述原则，确定不同埋深条件下，应力扩散起始位置及扩散角试验结果如表3所示。

表3 应力扩散起始位置及扩散角试验结果

注：H=15 cm的试验中，Ⅱ区应力略高于Ⅰ区应力，Ⅳ区应力基本上与Ⅰ区应力相等，因而假定应力从基底以上H/3位置开始扩散。

由表3可知，当基础埋深H=0时，应力从基底开始扩散；当基础埋深H>0时，应力从基底以上H/3位置开始扩散。综合各组试验结果，应力扩散角的变化范围为34°<θ<35°，可近似取土的内摩擦角作为应力扩散角。

2.2 附加应力影响深度

附加应力影响深度主要由Ⅲ区传感器确定，该区典型的应力-时间曲线如图7所示，其应力发展规律如下。

(1)离心机加速转动阶段：应力随加速度的增大近似线性增加，如图7中的OA段，转速稳定后，应力达到A点。

(2)加载阶段：随着上部竖向荷载的施加，浅层地基土体受到附加应力的影响，其应力不断增加，且呈非线性状态，如图7中的AB段，直至加载结束，应力达到最大值(B点)。对于深层地基土体而言，受附加应力的影响较小，其应力基本保持不变，如图7中的AC段所示。

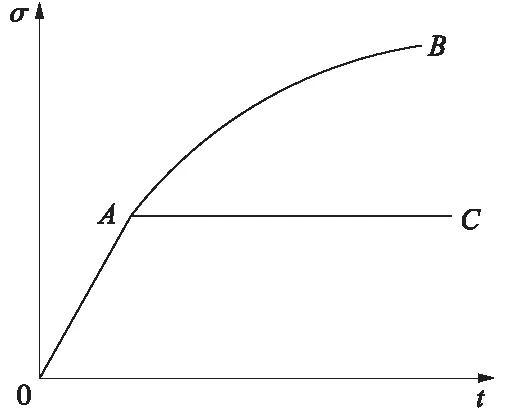
图7 应力-时间曲线

根据上述原则，确定不同埋深条件下，附加应力影响深度的试验结果如表4所示。

表4 附加应力影响深度的试验结果

注：H=10 cm的试验中，Ⅲ区最下层传感器的应力-时间曲线近似如图7中OAC所示，因而假定附加应力影响深度约为30 cm。

综合上述试验结果，考虑N=100的模型比换算为原型尺寸后，对于饱和砂土地基，附加应力影响深度在30 m(4倍基础宽度)左右，而建筑地基规范方法的计算结果仅为12.7 m，与试验结果差异较大。

3 结论与建议

通过开展离心模型试验,研究了饱和砂土地基中沉井基础在竖向荷载作用下的应力扩散效应。初步结论与建议如下。

(1)对于饱和砂土地基，当基础埋深H=0时，应力从基底开始扩散；当基础埋深H>0时，应力从基底以上H/3位置开始扩散。

(2)应力扩散角建议取土的内摩擦角φ。

(3)对于本文的试验结果，附加应力的影响深度在30 m左右，约为基础宽度的4倍。国内常用的《建筑地基基础设计规范》(GB50007—2011)的计算结果偏小。

[1] 杨灿文，黄民水.某大型沉井基础关键施工过程受力分析[J].华中科技大学学报(城市科学版)，2010，27(1):17-21.

[2] 冯广胜，盛华，罗瑞华.城市桥梁超大沉井关键施工技术[J].桥梁建设，2015，45(4):107-112.

[3] 葛春辉.钢筋混凝土沉井结构设计施工手册[M].北京:中国建筑工业出版社，2004.

[4] 徐金明，汤永净.分层总和法计算沉降的几点改进[J].岩土力学，2003，24(4):518-521.

[5] 陈祥福.深基础沉降计算方法和研究进展[J].土木工程学报，2004，37(6):70-77.

[6] Peck R B. Records of load tests on friction piles[R]. National Research Council U.S: Highway Research Board Special Report， 1961.

[7] 中华人民共和国铁道部.TB 10002.5—2005 铁路桥涵地基和基础设计规范[S].北京:中国铁道出版社，2005.

[8] 中华人民共和国交通部.JTG D63—2007 公路桥涵地基与基础设计规范[S].北京:人民交通出版社，2007.

[9] 中华人民共和国住房和城乡建设部.GB 50007—2011 建筑地基基础设计规范[S].北京:中国建筑工业出版社，2011.

[10] 中华人民共和国建设部.JGJ 94—2008 建筑桩基技术规范[S].北京:中国建筑工业出版社，2008.

[11] 上海市城乡建设和交通委员会.DGJ 08—11—2010 地基基础设计规范[S].北京:中国建筑工业出版社，2010.

[12] Terzaghi K， Peck R B. Soil Mechanics in Engineering Practice[M]. Second Edition. John Wiley & Sons， New York City，1967.

[13] AASHTO LRFD bridge design specifications， customary U.S. units.[M]. 4th ed. Washington， DC: American Association of State Highway and Transportation Officials， 2007.

[14] 刘金砺.桩基础设计与计算[M].北京:中国建筑工业出版社，1990.

[15] 徐光明，章卫民.离心模型中的粒径效应和边界效应研究[J].岩土工程学报，1996，18(3):80-85.

[16] 胡中波，马建林，徐力，等.沉井基础竖向承载特性的离心模型试验研究[J].铁道标准设计，2016，60(12):80-84.

Study on Foundation Stress Dispersion Effect in Saturated Sand Based on Centrifugal Model Test

DONG Xiao-peng1, MA Jian-lin1, HU Zhong-bo1,2, LI Jun-tang3, XU Li4

(1. School of Civil Engineering Southwest Jiaotong University, Chengdu 610031, China; 2. China Three Gorges Corporation, Beijing 100038, China; 3. China Railway Major Bridge Engineering Group Co., Ltd., Wuhan 430050, China;4. China Railway Major Bridge Reconnaissance & Design Group Co., Ltd., Wuhan 430056, China)

The open caisson foundation is more and more widely used in the big-span bridge engineering. In process settlement calculation, the determination of the additional stress distribution is always the focus and challenge. It mainly includes the initial position of stress dispersion, the size of diffusion angle and the influence depth of additional stress. Hence, the study of the properties of stress dispersion of the open caisson foundation is of great significance. The current approach given in the codes and the existing theory cannot be used for the open caisson foundations subjected to vertical loads under some limit conditions. To deal with this problem, the behaviors of settlement in saturated sand under vertical static loading are investigated based on several centrifugal model tests, and the influence scope of additional stress in saturated sand is determined. The test results may provide some references for engineering practices.

Centrifugal model test; Stress dispersion; Open caisson foundation; Settlement calculation; Saturated sand

1004-2954(2018)01-0084-04

2017-03-16;

2017-04-19

国家重点研发计划(2016YFC0802203-1)

董晓朋(1991—)，男，硕士研究生，主要从事地基基础方面的研究，E-mail：dxp19911126@163.com。

TU473.2

A

10.13238/j.issn.1004-2954.201703160001