交通荷载作用下土体黏弹塑性疲劳本构模型
陈泽南,浦少云,饶军应,方 琴,刘汉卿,郝至诚
(贵州大学土木工程学院,贵阳 550025)
交通荷载作用下土体黏弹塑性疲劳本构模型
陈泽南,浦少云,饶军应,方 琴,刘汉卿,郝至诚
(贵州大学土木工程学院,贵阳 550025)
路基工后沉降是路基填土在车辆动荷载及其自重作用下发生蠕变引起的,因此研究土体在交通荷载作用下的蠕变特性对预测路基工后沉降有较大意义。为利用流变力学理论成果,将车辆动荷载和路基土自重荷载简化的组合荷载做等效处理。基于分数阶微积分构建分数阶黏壶,将分数阶黏壶替换西原模型黏塑性体中常值黏性元件,即得到一种土体黏弹塑性疲劳本构模型。当组合荷载上限应力大于土体临界动应力时,模型为分数阶西原模型,可反映土体破坏型疲劳变形规律;反之,则为反映土体稳定型疲劳变形规律的广义Kelvin模型。结果表明:该模型能较好地描述交通荷载作用下土体疲劳变形特性,对试验数据拟合的相关系数在0.91以上。
交通荷载;工后沉降;蠕变;分数阶黏壶;黏弹塑性疲劳本构模型
在道路工程中,路基沉降一般分为两部分:一部分是填筑时的瞬时沉降;另一部分是填筑后的工后沉降。工后沉降是路基填土在自重及车辆动荷载作用下发生塑性变形累积引起的。土体在低动应力作用下累积塑性变形随时间推移趋于稳定,高动应力作用下应变加速增加直至破坏。交通荷载作用下土体的变形与时间有关,如果在其应力-应变关系中考虑时间因素,这就是岩土流变力学中的蠕变行为。研究土体在交通荷载作用下的蠕变特性对科学预测路基沉降具有重要的意义。
目前,国内外学者对动荷载作用下土体蠕变试验及蠕变模型方面进行了大量研究,已取得一定成果。
(1)土体蠕变试验方面:Werkmeister等[1]对粒料的shakedown行为进行研究,发现粒料永久变形呈现塑性蠕变(plastic creep)类型;雷华阳等[2]为研究动应力-应变、动模量的变化规律,对结构性软土开展了动三轴试验,研究发现振动波型对于结构性软土的动应力-应变影响不大,而对动弹模量的影响较大不容忽视;蔡英等[3]对成都黏土开展了动三轴试验研究,发现土体在循环荷载作用下的变形按永久应变-加载次数曲线的特征归为3类:稳定型、临界型和破坏型;刘晓红等[4]通过疲劳动三轴试验研究了循环荷载作用下原状结构红黏土动应变随振次的变化规律,测定了不同试验条件下红黏土的临界应力,并给出其估算公式;彭丽云等[5]用MTS动三轴仪对正融粉质黏土施加循环荷载进行单轴试验,研究了含水率、温度、动应力幅值等对土样变形的影响。
(2)土体蠕变模型方面:Monismith等[6]通过对粉质黏土重复加载动三轴试验的研究,首先提出预测路基土永久变形的指数模型;卢萍珍等[7]对软黏土进行了三轴蠕变试验,提出描述土体应力-应变关系的幂函数模型和应变-时间关系的双曲线函数蠕变模型,该模型是一个可较好反映软土蠕变特性的数学经验模型;黄明等[8]将路面上随机应力简化为表征其特性的一种简谐应力,将该简谐应力作用在描述土体蠕变变形的Kelvin体上,推导出路基土蠕变方程,并对模型进行了敏感性分析和对比分析;张洪亮等[9]为描述循环荷载下路基土3阶段变形特性,以五元件黏弹塑性体模拟土的受力变形,通过冲量等效把动应力转化为静应力,基于五元件黏弹塑性模型推导出了预估路基土永久变形理论模型。
从已有的研究成果来看,国内学者对动荷载作用下土体蠕变特性的研究主要集中在试验研究方面,蠕变模型的研究较少,而基于蠕变理论土体疲劳本构模型方面的研究成果尚未见到相关报道。鉴于此,本文试图建立一种基于蠕变理论的本构模型来描述交通荷载作用下土体疲劳变形特性,成果不仅可用于路基工程,亦能丰富岩土力学理论。
1 交通荷载作用下土体疲劳变形理论
1.1 交通荷载简化模型
交通荷载属于具有时间性和空间性的随机荷载,在理论分析时往往将它简化描述。无论是地震荷载、交通荷载或其他形式的动荷载,都可以通过最简单的简谐振动荷载来描述[8,10]。交通荷载作用下路基土蠕变既受土体自重影响,还受车辆动荷载影响。基于以上可将荷载做如下简化:车辆动荷载简化为正弦荷载,路基土自重简化为静荷载,两种荷载进行线性叠加,则路基土动静组合荷载计算模型(图1)为
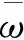
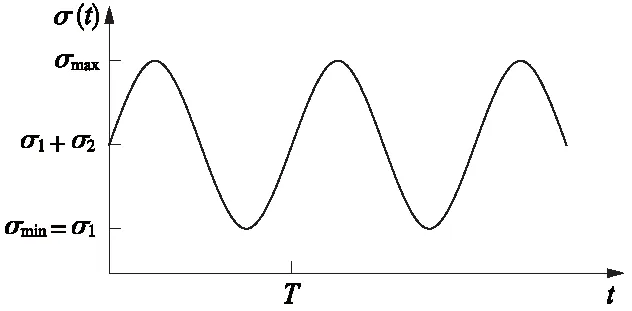
图1 动静组合荷载
1.2 循环荷载等效处理
郭建强等[11]为了建立循环荷载作用下岩石疲劳本构模型,将循环荷载做等效处理,借鉴该文等效思想,可将循环荷载σ(t)等效为
式中,σ为循环荷载σ(t)的等效应力;σdc为土体发生疲劳破坏的临界动应力。
分析式(2)可知:①当加载频率f→0时,加载荷载趋于静荷载,即等效应力σ→σav;②当σ<σav时,可得σmax<σdc,土体发生稳定型疲劳变形;③当σ>σav时,可得σmax>σdc,土体发生破坏型疲劳变形。
1.3 循环荷载作用下土体疲劳变形特性
循环荷载作用下土体疲劳变形根据累积应变-加载次数曲线可归纳为稳定型、临界型、破坏型三种类型[12-13](图2)。稳定型:土体在低动应力作用下,初期应变增加较快,随着土体逐渐压密,应变增速放缓,荷载加载到一定次数后,应变速率趋于稳定。临界型:在临界动应力范围内加载荷载,初期土体应变减速增加,荷载加载到一定次数后,应变呈波动状。破坏型:(1)土体在高动应力作用下,应变随加载次数增加而增加,荷载加载到一定次数后,土体结构破坏,强度降低,应变加速增加直至破坏;(2)加载的动应力远超临界应力,土体加速破坏。
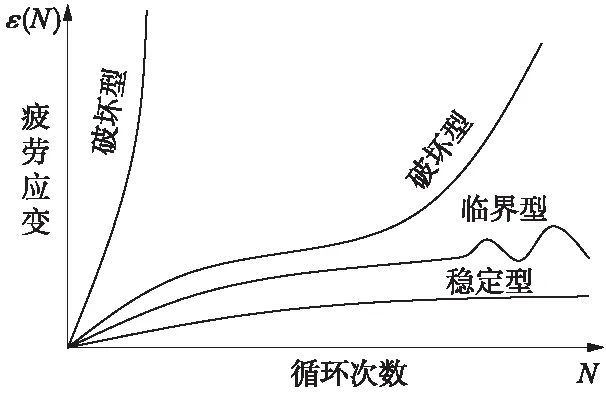
图2 土体疲劳变形曲线
2 分数阶疲劳黏壶
2.1 分数阶微积分定义
分数阶微积分是指微积分的阶数不是整数而是任意的实数或复数。它具有多种定义方法,在岩土材料蠕变研究中最常用的是Riemannn-Liouville型分数阶微积分[14]。函数f(t)在可积分区间[0,t]上的i阶Riemannn-Liouville积分定义为
相对应函数f(t)的i阶Riemannn-Liouville微分定义为

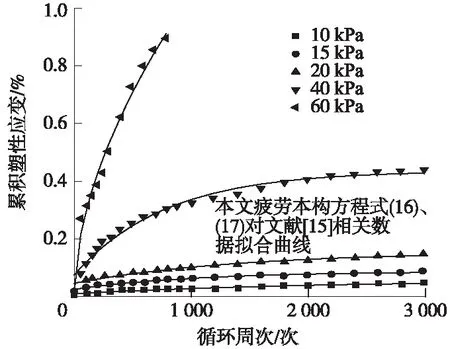
式中,i为微积分阶数,i>0,且m-1 式中,η为黏性疲劳系数,其物理量纲为[应力·时间n];n为分数阶微积分阶数,反映土体变形速率参数;η、n可通过试验测定。 当σ(t)=σ时,即保持应力不变,根据Riemannn-Liouville型分数阶微积分算子理论,对式(7)两侧进行分数阶积分,分数阶疲劳黏壶的疲劳本构方程为 图3分数阶黏壶 传统多元件组合模型中黏壶为定值黏壶时,可描述土体减速、等速蠕变阶段,无法描述土体加速蠕变。为能较完整描述岩土材料的变形特性,许多学者运用分数阶微积分在曲线描述上的优势,基于分数阶微积分构建分数阶黏壶,将其代替传统力学模型中定值黏壶,以描述岩土材料各种蠕变阶段及类型。 本文基于西原模型建立一种描述交通荷载作用下土体疲劳变形的模型。为使模型更准确反映土体变形规律,将西原模型Bingham体中的黏壶换成分数阶疲劳黏壶,即得到土体黏弹塑性疲劳本构模型(图4)。 图4 土体黏弹塑性疲劳本构模型 对于图4所示模型,当σ>σav时,分数阶Bingham体参与变形,模型为分数阶西原模型,描述土体破坏型疲劳变形;当σ<σav时,分数阶Bingham体不参与变形,模型退化为广义Kelvin模型,描述土体稳定型疲劳变形。 (1)Hook体疲劳本构模型 Hook体疲劳本构模型[11]由单个弹性疲劳元件构成(图5),应力-应变关系符合Hook定律,其蠕变方程为 因t=NT,(8)式代换整理为以N为变量的疲劳本构方程 式中,εⅠ(t)为t时刻Hook体总应变;εⅠ(N)为循环荷载作用N次时Hook体总应变;E1为弹性疲劳系数,物理量纲为[应力]。 图5Hook体疲劳本构模型 (2)Kelvin体疲劳本构模型 Kelvin体疲劳本构模型[11](图6)由弹性与黏性疲劳元件并联而成。对于组合模型:串联条件下,串联各部分应力相等,总应变等于各个部分的应变之和;并联条件下,并联各部分应变相等,总应力等于各部分的应力之和。其状态方程为 式中,σ1、σ2、ε1、ε2分别为模型中弹性及黏性疲劳元件的应力和应变;εⅡ为模型总应变。 根据蠕变相关理论,并进行变量代换可得 式中,E2为弹性疲劳系数,物理量纲与E1一致;η1为黏性疲劳系数,物理量纲为[应力·时间]。 将式(10)、式(11)联立,对两端积分可得模型的疲劳本构方程为 图6 Kelvin体疲劳本构模型 (3)分数阶Bingham体疲劳本构模型 分数阶Bingham体疲劳本构模型(图7)由分数阶疲劳黏壶与塑性疲劳元件并联而成。当σ<σav时,该模型不参与变形,εⅢ=0;当σ>σav时,其状态方程为 式中,σ1、ε1分别对应分数阶疲劳黏壶的应力和应变;εav为塑性疲劳元件应变;εⅢ为模型的总应变。联立式(6)、式(13)可得 式中,η2为模型的黏性疲劳系数。 动静组合荷载等效:σ(t)=σ,加载参数确定后则等效应力σ为常量。根据Riemannn-Liouville型分数阶微积分算子理论,对式(14)两端积分,可得模型的疲劳本构方程为 图7 分数阶Bingham体疲劳本构模型 建立的土体黏弹塑性疲劳本构模型(图4)由Hook体、Kelvin体、分数阶Bingham体串联而成。 当σ<σav时,退化为描述土体稳定型疲劳变形规律的广义Kelvin体模型,其疲劳本构方程为 分析式(16)可得如下结论。 (1)当N=0时,ε(0)=σ/E1,土体的变形为在荷载平均值σav作用下的瞬时弹性变形。 (2)当N→∞时,ε(N)→σ/E1+σ/E2。即加载循环荷载上限应力σmax小于土体临界动应力σdc,随加载次数N逐渐增大直至无穷时,土体逐渐压密,应变ε(N)趋于稳定,收敛于σ/E0+σ/E1,即所有的应力都由弹簧承担。也可看出,土体仍处于等速疲劳变形阶段,不会随循环次数增加进入加速阶段,即土体不会发生疲劳破坏。 当σ>σav时,分数阶Bingham体参与作用,为描述土体破坏型疲劳变形规律的分数阶西原模型,此时模型的疲劳本构方程为 分析式(17)可得如下结论。 (1)当N=0时,ε(0)=σ/E1,土体变形为在荷载平均值σav作用下的瞬时弹性变形。 (2)当N→∞时,广义Kelvin体疲劳本构方程部分:εⅠ(n)+εⅡ(n)→σ/E1+σ/E2,随N增加应变趋于定值;分数阶Bingham体部分,分情况讨论:当微积分阶数n=0时,分数阶黏壶为理想弹性体,变形为定值;当0 当σ<σav时,模型为含E1、E2、η1的三参流变模型,反映土体稳定型疲劳变形;当σ>σav时,为含E1、E2、η1、η2、n的五参流变模型,可反映土体破坏型疲劳变形规律。1stOpt软件在非线性回归、曲线拟合、非线性复杂模型参数估算求解等领域已得到学术界的广泛认可,本文运用1stOpt软件中模拟退火算法对模型本构方程式(16)、(17)的参数进行求取,并对相关试验数据进行拟合。 选取加载方式与动静组合荷载计算模型一致的2组路基土动三轴试验,用相关试验数据对模型进行适用性验证。 冷伍明等[15]为研究交通荷载作用下路基粗粒土动力响应特性,对粗粒土开展了振动频率为1 Hz的正弦波循环荷载下的动三轴试验,以模拟速度50 km/h的重载列车对路基土的作用。其所施加动应力下限值为 式中,qcyc,min为轴向静偏应力,模拟粗粒土受到的列车静荷载,qcyc,min=15 kPa;σ′3,c为围压。 土体临界动应力σdc是判断循环荷载下土体是否发生破坏型变形的重要参数,易推算出含水率为9.3%的饱和土样的临界动应力幅值经验公式 张勇等[16]通过对饱和软黏土进行室内小排水动三轴试验,研究循环荷载作用下软黏土应变的发展规律,提出不同影响因素下累积应变拟合模型。试验仪器采用双向振动三轴仪,施加频率为4 Hz的正弦波循环荷载模拟交通荷载作用,以围压、动应力幅值、静偏应力为变量分别设置了5组对比试验。 模型本构方程式(16)、(17)对文献[15],[16]中累积应变与振动次数曲线进行拟合及模型参数的求取。文献[15]、[16]中相关试验数据见表1,对试验数据的拟合参数见表2,拟合曲线见图8、图9。 表1 文献[15]、[16]相关数据 表2 土体黏弹塑性疲劳本构模型对文献[15]、[16]试验结果的拟合参数 图8 黏弹塑性疲劳本构模型对路基粗粒土疲劳变形的拟合 图9 黏弹塑性疲劳本构模型对软黏土疲劳变形的拟合 由表2及图8、图9可知:土体黏弹塑性疲劳本构模型对粗粒土和软黏土两种路基填土累积变形-加载次数曲线进行拟合达到了较高的拟合精度,相关系数均在0.9以上。当土体疲劳变形为破坏型,相关系数均可达0.98以上,能满足工程上对路基变形预测的精度要求。虽然模型对稳定型的拟合精度比破坏型低,但是相关系数仍达到0.91以上,最高也达到了0.995。数据表明:本模型可较好地模拟路基土疲劳变形。 路基粗粒土拟合曲线见图8,拟合参数见表2。30 kPa围压下,当σd<σdc,疲劳变形处于稳定型,E1、E2、η1三个参数随动应力幅值增加变化范围不大,且有减小趋势;当σd>σdc,疲劳变形处于破坏型,因土骨架破坏,受力体系情况复杂,参数规律不明显。但处于同一数量级。 图10 当σd<σdc时软黏土E1与σd关系 图11 当σd<σdc时软黏土E2与σd关系 图12 当σd<σdc时软黏土η1与σd关系 分数阶微积分的阶数n的拟合数据表明,破坏型曲线的n值大于1,同种土体在围压相同的情况下,n值有随加载应力幅值增大而增加的趋势。 (1)把交通荷载简化为动静组合荷载(循环荷载),可更好地利用流变力学成果,基于塑性变形的等效性和连续性对循环荷载进行等效处理。 (2)基于分数阶微积分理论构建分数阶疲劳黏壶,用分数阶疲劳黏壶替代西原模型中的常值黏壶,建立了一种基于西原模型的土体黏弹塑性疲劳本构模型。最后运用1stOpt软件中模拟退火算法对循环荷载作用下土体蠕变试验的ε-N曲线进行了参数的求取及曲线的拟合,验证了模型的适应性。 (3)所建立的土体黏弹塑性疲劳本构模型能够描述土体稳定型、破坏型两种疲劳变形类型。 (4)对粗粒土和软黏土的ε-N曲线进行拟合的结果表明,本文提出的土体黏弹塑性疲劳本构模型能较好地描述不同土体疲劳变形特性。 [1] Werkmeister S, Dawson A R, Wellner F. Pavement design model for unbound granular materials[J]. Journal of Transportation Engineering, 2004, 130(5):665-674. [2] 雷华阳,姜岩,陆培毅,等.交通荷载作用下结构性软土动应力-动应变关系试验研究[J].岩石力学与工程学报,2007,27(S1):3052-3057. [3] 蔡英,曹新文.重复加载下路基填土的临界动应力和永久变形初探[J].西南交通大学学报,1996,31(1):1-4. [4] 刘晓红,杨果林,方薇.武广客运专线路堑红黏土临界动应力疲劳试验研究[J].湘潭大学学报(自然科学版),2010,32(2):57-62. [5] 彭丽云,刘建坤.正融粉质黏土在循环荷载作用下的变形特性研究[J].岩土工程学报,2010,32(4):567-572. [6] Monismith C L, Ogawa N, Freeme C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. TRR,1975(537):1-17. [7] 卢萍珍,曾静,盛谦.软黏土蠕变试验及其经验模型研究[J].岩土力学,2008,29(4):1041-1044. [8] 黄明,刘新荣.交通荷载作用下高填方路堤的工后蠕变模型探析[J].解放军理工大学学报,2011,12(1):54-58. [9] 张洪亮,边祥芹,王玉兰.重复荷载作用下路基土黏弹塑性永久变形预估[J].长安大学学报(自然科学版),2010,30(2):29-33. [10] 陈勇.交通荷载对低路堤高速公路路基影响的数值模拟研究[D].南京:河海大学,2006. [11] 郭建强,黄质宏.循环荷载作用下岩石疲劳本构模型初探[J].岩土工程学报,2015,37(9):1698-1703. [12] 刘晓红,杨果林,方薇.红黏土临界动应力与高铁无碴轨道路堑基床换填厚度[J].岩土工程学报,2011,33(3):348-353. [13] 周文权,冷伍明,刘文劼,等.低围压循环荷载作用下饱和粗粒土的动力特性与骨干曲线模型研究[J].岩土力学,2016,37(2):415-423. [14] 靳丹丹,马芳芳,么焕民. Riemann-Liouville分数阶微积分的定义及其性质[J].哈尔滨师范大学学报(自然科学版),2011,27(3):21-23. [15] 冷伍明,刘文劼,周文权,等.振动荷载作用下重载铁路路基粗颗粒土填料临界动应力试验研究[J].振动与冲击,2015,34(16):26-30. [16] 张勇,孔令伟,郭爱国,等.循环荷载下饱和软黏土的累积塑性应变试验研究[J].岩土力学,2009,30(6):1542-1548. Visco-elastic-plastic Fatigue Constitutive Model for Soil under Traffic Loading CHEN Ze-nan, PU Shao-yun, RAO Jun-ying, FANG Qin, LIU Han-qing, HAO Zhi-cheng (College of Civil Engineering, Guizhou University, Guiyang 550025, China) The post settlement of subgrade is caused by subgrade creep under self-weight and vehicle dynamic loading, and it is of great significance to study soil creep properties under traffic loading for subgrade settlement prediction. Based on the theoretical achievements of rheological mechanics, the combined loading simplified by vehicle dynamic loading and self-weight loading of subgrade soil is processed equivalently. A fractional-order dashpot based on fractional calculus is constructed, constant dashpot in the visco-plastic body of nishihara’s model is replaced with fractional-order dashpot, a visco-elastic-plastic fatigue constitutive model for soil under traffic loading is obtained by doing so. When the upper stress of combined loading is larger than critical dynamic stress of soil, the model is fractional-order nishihara’s model, which can reflect the destructive deformation law of soil; otherwise, it is a generalized Kelvin model, which can reflect stable deformation law of soil. Results show that this model can better reflect the creep behavior of soil under traffic loading and its fitted correlation coefficient of test data is above 0.91. Traffic loading; post-construction settlement; Creep; Fractional-order dashpot; Visco-elastic-plastic fatigue constitutive model 1004-2954(2018)01-0068-06 2017-03-16; 2017-04-08 国家自然科学基金(51608141);贵州大学引进人才科研项目(贵大人基合字(2015)16) 陈泽南(1991—),男,硕士研究生,主要从事岩土工程等方面的工程实践、科研工作,E-mail:595875805@qq.com。 浦少云(1993—),男,硕士研究生,主要从事岩土工程相关方面研究及工程实践工作,E-mail:2290605640@qq.com。 U213.1+57 A 10.13238/j.issn.1004-2954.2017031600042.2 分数阶疲劳黏壶
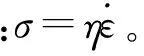
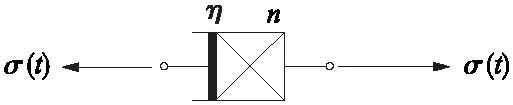
3 黏弹塑性疲劳本构模型
3.1 模型的建立
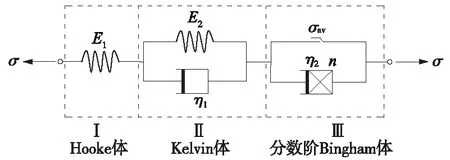
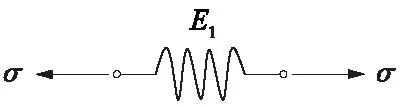
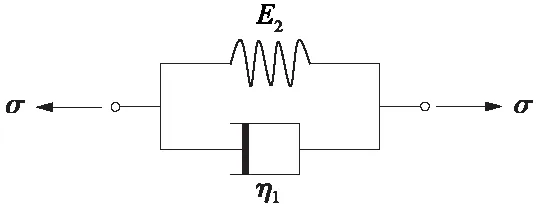

3.2 土体黏弹塑性疲劳本构方程
4 模型适用性验证
4.1 模型参数的确定
4.2 试验分析及模型的拟合
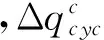

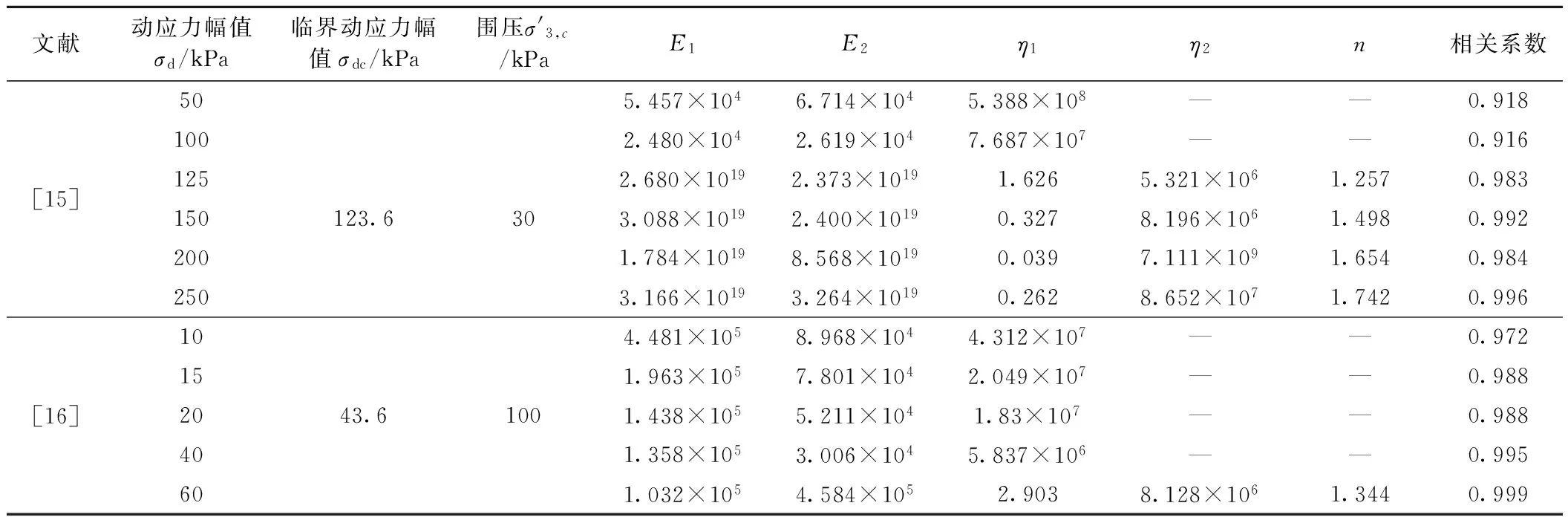

4.3 拟合结果分析
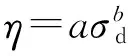
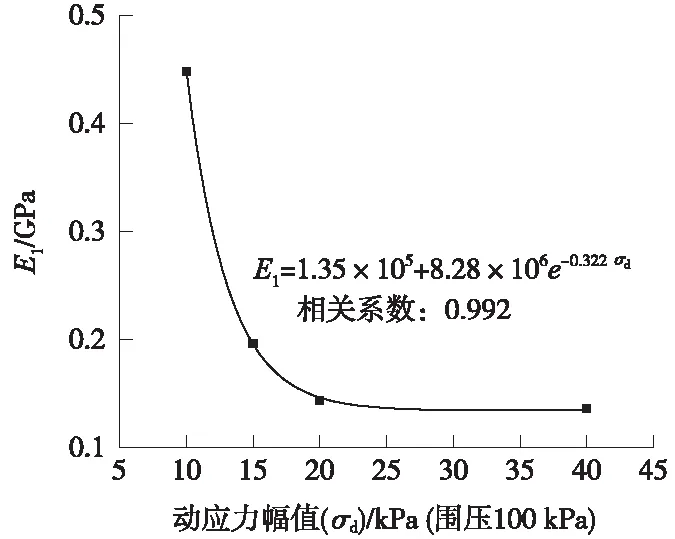
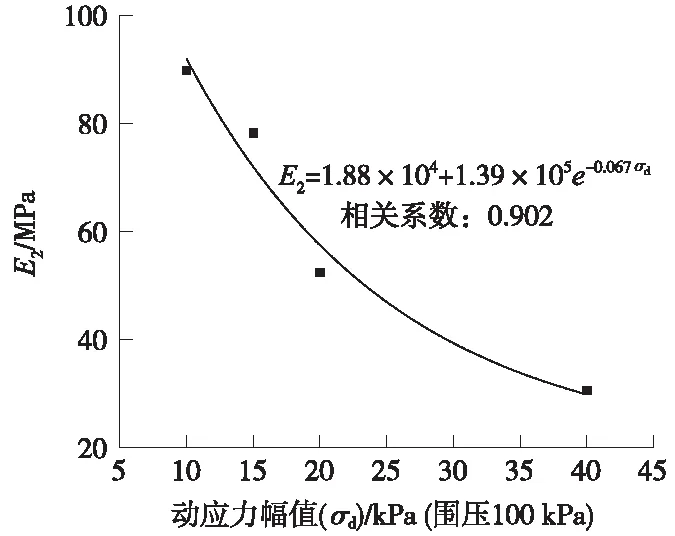
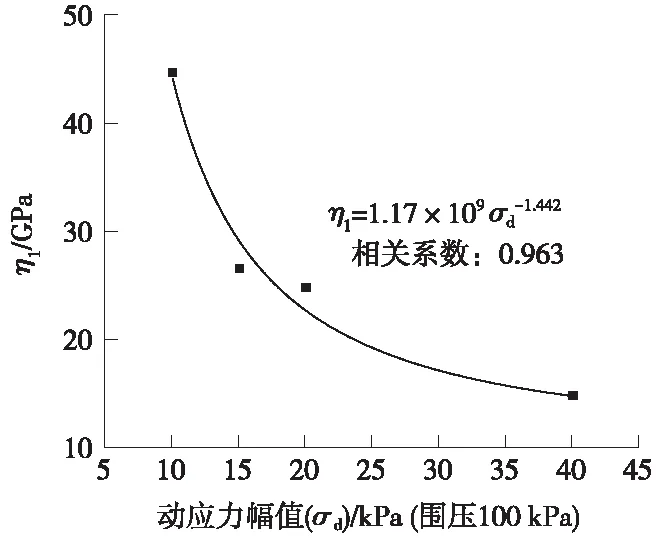
5 结论

