基于GA-GM(1, N,α)幂模型的铁路客运量预测

许 锟,鲍学英,王起才

(兰州交通大学土木工程学院,兰州 730070)

基于GA-GM(1, N,α)幂模型的铁路客运量预测

许 锟,鲍学英,王起才

(兰州交通大学土木工程学院,兰州 730070)

针对在铁路客运量预测领域传统的灰色预测模型不能反映真实系统的非线性结构特点及其背景值的赋值不合理的问题,提出使用对系统相关因素引入幂指数且经过背景值优化的GM(1, N, )幂模型进行客运量预测。背景值优化时设置待定参数,利用线性组合结构重新计算背景值。对此模型产生的较多的待定参数,采用能够并行运算、全局寻优的遗传算法进行一次性求解。最后使用此模型对甘肃省铁路客运量进行建模预测,并与传统GM(1, N)模型、GM(1, N)幂模型进行对比分析。结果证明, GM(1, N, )幂模型具有更高的预测精度,对铁路客运量预测有一定的应用和研究价值。

灰色模型；遗传算法；铁路客运量；预测；背景值优化

铁路部门的运输能力影响着整个国民经济的发展[1]。对铁路客运量进行有效的预测是为铁路运输部门作出合理规划提供依据[2]。因此针对铁路客运量预测的研究具有充分的必要性和合理性。

骆泳吉[3]建立了非线性回归模型并对京沪高铁日客运量做了预测，结果显示其精度和稳定性均优于BP神经网络模型；Cheng[4]采用RBF神经网络建模方法对哈尔滨太平国际机场客流量进行了预测，结果证明其模型预测精度较高；汪健雄等[5-7]也建立了不同的神经网络预测模型，均对客运量预测效果较好；侯丽敏和Yuan均构建了GM(1，1)与线性回归的组合模型[8-9]，分别对河南省铁路客运量和拉萨市出租车客流量进行了预测，且取得较高预测精度；Chen[10]建立了一种残差GM(1，1)模型，并在陕西货运量预测问题中表现良好。冯冰玉[11]提出一种BP神经网络与灰色GM(1，1)相结合的新型组合模型，在兰州至中川机场铁路客运量预测应用中表现出较高的预测精度。

以上针对客运量预测的研究包括了非线性的神经网络类方法和基于贫信息、少数据的灰色预测方法，且都取得了优良的预测精度。但是在灰色预测领域鲜有能够对系统进行非线性预测的模型。铁路客运量的预测是一个对非线性结构系统的规律进行预测的过程，传统的灰色预测模型描述这样的系统难以避免较大的误差。

此外，黄元生[12]对灰色预测模型背景值赋值的不合理性进行了证明；周清[13]经过实例分析证明对于低增长序列，背景值最佳生成系数法能有效提升精度；徐宁[14]基于误差最小化优化了GM(1，1)模型的背景值，使其同时具有无偏性和最小误差性。

针对以上问题，本文提出使用经过背景值优化的GM(1，N，α)幂模型来对铁路客运量进行预测。通过引入幂指数使相关变量能够对系统特征序列产生非线性的影响，同时使用线性结构的背景值优化方法进一步提升模型的精度。受李祚泳[15]和邵良彬[16]使用遗传算法优化GM(1，1)模型的启发，本文采用具有并行计算，全局寻优特点的遗传算法对模型的多个待定参数进行求解。

1 背景值优化的GM(1，N，α)幂模型的建立

1.1 GM(1，N)幂模型

而

⋮

为GM(1，N)幂模型。

相对于传统的GM(1，N)模型，GM(1，N)幂模型具有更好的非线性结构。而现实生活中绝大多数系统都是非线性的，这就意味着具有非线性结构的幂模型能更好地描述真实系统。GM(1，N)幂模型中γi即为对应相关变量的幂指数，用以反映对应相关变量对系统产生的非线性作用。当所有幂指数均为1时，模型即退化为传统GM(1，N)模型。

为GM(1，N)幂模型的影子方程。

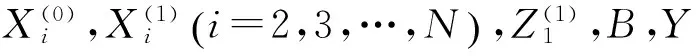
(1)上述影子方程的解为

(3)经过累减还原后的预测值为

在实际建模时，为了防止模型在参数识别时出现数据矩阵漂移现象，应对数量级较大的原始数据进行初值化等数据变换。

1.2 背景值优化

对模型预测精度影响最大的因素之一就是背景值，因此，背景值的构造是提高模型精度的一个有效突破口。文献[11]已经论证过，紧邻均值生成对背景值的赋值并不合理。本文采取线性结构来优化背景值。

传统的背景值为紧邻均值生成，即

采用线性组合结构优化的背景值为

其中，α为待定参数。

将新构建的背景值代入方程(1)中，即变为

相关项合并后即可得

解之得

设辅助参数

则由式(14)可得

2 使用遗传算法(GA)优化参数

遗传算法(Genetic Algorithm)是20世纪70年代发展出来的一种基于自然选择、遗传学理论和适者生存原理的最优化全局搜索算法[17]。它能够对目标空间进行随机搜索。通过对问题的可能解进行编码、选择、交叉、变异、解码等一系列遗传操作，逐步地得到问题的最优解。由于它不受搜索空间限制性条件的约束，遗传算法不要求目标函数可微可导。因此，它具有简洁易懂、适用范围广和便于操作的优良特性。

使用遗传算法进行参数优化的步骤如下。

(1)编码。初始化种群后，本文采用实数编码的方式来构建染色体[18]。不仅可以缩短个体的长度，也能省去解码的过程。

(2)计算适应度。以幂模型的平均相对误差最小化为目标，建立适应度函数如下

(3)选择。本文采用“轮盘赌”法进行选择操作。使适应度大的个体被选中的概率大，而适应度小的个体被选中的概率小。个体被选中的概率为

式中，fk为第k个个体的适应度，n为种群规模。

(4)交叉。交叉操作是以某个概率交换2个个体的部分基因，从而产生新个体，实现对目标空间的全局搜索。此处使用实数交叉法。个体ws和个体wg在位置点的交叉操作产生的新个体如式(17)、(18)所示，其中为之间的随机数。

(5)变异。此处采用非均匀变异：设个体，对变异点进行变异操作后得到的新基因值为

式中，Rd(0，1)为以相同概率从0、1中任取一个；r为[0，1]上的随机数；G为当前代数；T为终止代数；b为参数，进化代数G对随机数影响的大小由它决定。

(6)重复步骤2至步骤5，直到满足终止条件。

本文使用遗传算法对GM(1，N，α)幂模型进行参数优化时直接对所有未知参数求解，结果代入幂模型即可进行模拟运算。

通过遗传算法寻找模型参数最优解的优势在于它能够并行运算，同时优化所有要求的参数。避免了通过公式推导来求背景值优化参数的繁琐过程。遗传算法的计算过程清晰，更加简单易用。

3 应用实例

为了对比分析，本文将分别建立传统GM(1，N)模型、GM(1，N)幂模型和GM(1，N，α)幂模型对甘肃省2005～2014年的铁路客运量进行预测。其中选择2005～2011年这7年的数据来进行建模，并对2012～2014年的甘肃省铁路客运量作建模样本外预测，基于平均相对误差分析对比建模精度。

3.1 原始数据

在研究中，基于相关文献查阅和关联度比较选取了对铁路客运量影响较明显的甘肃省地区的生产总值和居民消费水平作为相关因素序列。

(1)甘肃省地区生产总值：代表着甘肃省地区一年内的生产总值，能够反映整个地区的经济发展情况。对当地的客运量有着直接的影响。

(2)居民消费水平：反映当年甘肃省地区居民消费支出情况。居名消费水平越高意味着居民选择出行的可能性越大，对客运量增长有较明显的影响。相关具体数据见表1。

表1 原始数据统计

注：数据来源于甘肃省统计局.

3.2 平均相对误差计算

分别用3种建模方法对系统进行建模预测后，得到结果见表2。根据2005～2011年的相关数据建立的传统GM(1，N)模型平均相对误差为16.02%，而GM(1，N)幂模型的平均相对误差减小到4.58%，当使用经过背景值优化的GM(1，N，α)幂模型时平均相对误差减至3.31%，模型预测精度达到96.69%。

表2 3种模型的模拟和预测结果

4 结语

(1)针对铁路客运量预测过程中的非线性系统特征提出使用经过线性结构背景值优化的GM(1，N，α)幂模型来进行模拟和预测。引入幂指数的模型能够更准确地反映真实系统的非线性结构特点。

(2)利用遗传算法并行全局优化搜索的特点对模型的参数进行寻优求解。遗传算法能针对多参数求解问题提供过程清晰、操作简便的计算过程，较为快速地寻找到参数的最优解。

(3)在对甘肃省2005～2014年铁路客运量的预测实例分析中的结果表明：GM(1，N)幂模型相对于传统的GM(1，N)模型预测精度有明显的提升，同时经过背景值优化的GM(1，N，α)幂模型能够更好地描述系统行为规律，平均相对误差明显减小。证明此模型在铁路客运量预测领域有一定的实用性。

[1] 曹庆山.铁路运输与社会经济适应性分析[D].成都：西南交通大学，2010.

[2] 宋光平.铁路货运量预测方法研究[D].北京：北京交通大学，2007.

[3] Lou Yong ji，Liu Jun，Sun Xun，et al. Regression model for daily passenger volume of high-speed railway line under capacity constraint[J]. Journal of Central South University，2015(9):3666-3676.

[4] Cheng S， Xu J， Mu Q， et al. A Terminal Departure Passenger Traffic Prediction Method Based on the RBF Neural Network[C]∥ Cota International Conference of Transportation Professionals. 2014:31-38.

[5] 汪健雄，刘春煌，单杏花，朱建生.基于双层次正交神经网络模型的铁路客运量预测[J].中国铁道科学，2010(3):126-132.

[6] 王浩，郭瑞军.改进PCA-BP神经网络模型在公路客运量预测的应用[J].大连交通大学学报，2016(2):1-5.

[7] Yan Q， Wang H， Wang H. Prediction of Taxi Passenger Volume Based on a Gray Linear Regression Combined Model[C]∥ International Conference on Transportation Engineering. 2015:335-341.

[8] Yuan C， Lin W， Jiao P. Prediction Method for Freight Volume Based on Residuals Improved GM (1，1) Model[C]∥ ICTE 2013@sSafety， Speediness， Intelligence， Low-Carbon， Innovation. ASCE， 2013:140-146.

[9] 侯丽敏，马国峰.基于灰色线性回归组合模型铁路客运量预测[J].计算机仿真，2011(07):1-3，30.

[10] Chen Y， Zha W. Prediction of the Traffic Volume of Henan Province with a BP Neural Network[J]. Joint Bone Spine Revue Du Rhumatisme， 2015，81(28):542-542.

[11] 冯冰玉，鲍学英，王起才，董朝阳.新型组合模型在铁路客运量预测中的应用[J].铁道标准设计，2015，60(12):6-9.

[12] 黄元生，陈子儒.灰色预测模型背景值赋值不合理性的证明及改进[J].电子测试，2013(13):70-71.

[13] 周清，王奉伟.灰色预测模型背景值改进方法比较分析[J].东华理工大学学报(自然科学版)，2015(2):231-234.

[14] 徐宁，党耀国，丁松.基于误差最小化的GM(1，1)模型背景值优化方法[J].控制与决策，2015(2):283-288.

[15] 李祚泳，张明，邓新民.基于遗传算法优化的GM(1，1)模型及效果检验[J].系统工程理论与实践，2002(8):136-139.

[16] 邵良杉，马寒，温廷新，张银玲.遗传算法优化的GM(1，1)模型研究[J].统计与决策，2015(4):22-24.

[17] 席裕庚，柴天佑，恽为民.遗传算法综述[J].控制理论与应用，1996(6):697-708.

[18] 何祥卫.基于遗传算法的铁路纵断面优化研究[J].铁道标准设计，2014(6):14-17.

Railway Passenger Volume Forecasting based on GA-GM (1, N,α ) Power Model

XU Kun, BAO Xue-ying, WANG Qi-cai

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to reflect the nonlinear structural characteristics of the real system in railway passenger volume forecasting and set the background value of gray prediction models in a reasonable way, a GM(1,N,α) power model with background value optimization is proposed for forecasting passenger volume. The linear combined structure with a probable parameter is used to recalculate the background value and more probable parameters are solved by a genetic algorithm that can perform parallel operation and global optimization for one-time solution. Finally, forecasting railway passenger volume in Gansu Province is conducted with this model. By comparing it with the traditional GM (1,N,α) model and GM (1,N,α) power model, we find that GM(1,N,α)power model has higher prediction accuracy and proves applicable in railway passenger traffic forecasting.

Grey model; Genetic algorithm; Railway passenger volume; Forecast; Background value optimization

1004-2954(2018)01-0006-04

2017-03-21;

2017-04-05

长江学者和创新团队发展计划滚动支持(IRT15R29)，兰州交通大学优秀科研团队资金资助(201606)，国家自然科学基金(51768034)

许 锟(1994—)，男，陕西西安人，硕士研究生。

鲍学英(1974—)，女，教授，从事铁路运输管理及决策研究，E-mail:813257032@qq.com。

U293

A

10.13238/j.issn.1004-2954.201703210007