大数据统计方法综述

叶小青，汪政红，吴 浩

(中南民族大学 数学与统计学学院，武汉 430074)

随着通讯和信息技术的高速发展，全球数据爆炸性地增长.面对铺天盖地的海量大数据，有效的数据分析与挖掘将推动国家、企业乃至整个社会的高效、可持续发展.值得强调的是，在大数据分析与挖掘任务中，统计分析的研究受到更为广泛的关注和重视.而大部分传统统计方法对大数据的研究存在局限性：一是传统统计方法适合分析单个计算机存储的数据，无疑导致了数据处理和整合的困难；二是传统统计方法难以适应大数据源的高速性和实时性等特点.因此，为了适应大数据这一新的研究对象，传统统计学必须进行改进，以更好地服务于人类.目前国内外将大数据和传统统计学相结合的研究文献并不多，使得大数据背景下统计分析的研究成为学术界关注的热点难点问题，其代表性文献集中于三大方面：分治算法、抽样法和在线更新算法.

第一，分治算法是将初始大数据集分成适合当前计算管理能力的K个子集，先对每个子集做统计分析，然后综合K个子集的分析结果.分治算法通过对子集的平行计算可以缩减计算成本，但是，如何总结K个子集的估计结果，才能使最终的估计结果更有效？为了得到最终有效的估计量，部分研究者提出了不同的估计方法，如Li等对大数据集的单参数回归模型提出了二阶段法，其研究结果表明二阶段法可以显著地降低计算成本，且估计量具有渐进正态性[1].Lin和Xi对非线性回归方程的参数估计提出了有效的聚合估计(AEE,Aggregated Estimating Equation)，研究结果显示AEE估计量具有一致性，而且能显著地缩减计算成本[2].在应用方面，AEE估计方法适合于大型数据立方和数据流.Xu等对广义回归方程提出了非参数分布核估计方法(DKR,Distributed Kernel Regression)，其研究结论为：在适当划分子样本集的条件下，DKR估计方法具有一致性[3].Chen和Xie(2014)运用惩罚似然函数估计各子集的广义线性回归方程，并利用多数表决法得到大数据集的最终估计量，研究结果表明估计量具有符号一致性[4].

第二，抽样法的基本思想是从初始大数据中随机提取子样本代替原始数据对模型进行估计、预测以及统计推断.抽样法的难点在于设计子样本的概率分布.最简单的概率分布是均匀分布，大量研究文献表明运用统计杠杆值作为子样本的概率分布优于均匀分布(Mahoney等[5]，Drineas等[6]).Ma和Sun也认为利用杠杆值作为子样本的概率分布能准确有效地提取大规模样本信息，并且从统计角度研究了基于杠杆值抽样算法估计量的性质[7].

第三，随着科学技术的不断普及，大数据的规模和程度不断地增大，具有实时更新特性.例如在银行的存款中，每天都有成千上万的客户利用自动取款机或人工服务进行交易，每一位客户对自己的银行账号进行操作，对于银行的整个数据系统来说是极小的一部分，面对这样实时在线更新的大数据，如何获得计算效率高、成本低的算法呢？Schifano等扩展了Lin和Xi的理论方法，研究了广义非线性模型的回归系数和标准误的在线更新估计量，其研究结果显示在线更新估计量具有一致性，而且有限样本仿真模拟表明在线更新估计量具有较小的偏误[8].Wang等基于Schifano研究结论首次提出了标准变量选择的在线更新模型，并根据AIC、BIC和DIC信息准则来选择最优变量[9].

从以上大数据统计分析的研究进展来看，尽管研究成果尚不丰富，仍处于起步阶段，但对现有成果的梳理与总结，可以为关注大数据统计分析的研究者、教学者提供借鉴.

1 分治算法理论

分治算法是将初始大数据集分成适合当前计算机管理能力的K个子集，先对每个子集做统计分析，然后综合K个子集的分析结果.下面详细介绍几种有效的分治算法.

1.1 二阶段法

Li等提出了二阶段法，其基本思想：第一阶段将整个数据集划分为若干子样本，使得每个子样本都适合目前的计算机管理能力，估计每个子样本参数；第二阶段对每个子样本估计结果取平均值.

假设x1,x2,…,xn是独立同分布样本，此处xi可以是随机变量或随机向量.为了清晰表达二阶段估计算法，将样本表示如下：

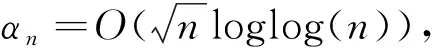
1.2 AEE估计法

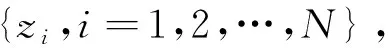
1.3 DKR估计法

Xu等提出了非参数分布核回归(DKR)方法来估计参数方程，该方法不仅具有普适性，而且不依赖于任何真实模型的参数假设.

设Y∈[-M,M]⊂R是因变量，其界限M>0，X是解释变量且X∈κ⊂Rd，κ为d维空间一紧集.总体Z=[-M,M]×κ分布未知，且设S={zi=(yi,xi),i=1,2,…,N}是来自Z的N个独立样本观测值.记f:κ→R为X与Y之间的潜在函数关系.在大数据背景下，如何估计函数关系f，非参数分布核回归算法具体如下：

1) 假设S平均随机分成m份，每份样本容量为n=N/m，m个子样本标识分别为S1,S2,…,Sm；

2) 记TM[·]为阈值M的截取算子，基于子样本Sj，得fj估计值为：

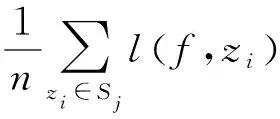
1.4 多数表决法

Chen和Xie为广义线性模型的参数估计提出了一种分治算法，其估计思想为基于子样本的似然函数，加入惩罚项，称为广义似然函数，并最大化广义似然函数估计子样本参数，最后运用多数表决法得出大样本数据的综合估计量，通过仿真和数据实例表明该方法能极大地缩减计算时间和计算存储空间.

假设在给定X=(x1,…,xn)T的情况下，y=(y1,…,yn)T条件分布为典型指数分布，那么似然函数为：

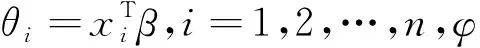
其中，b(θ)=[b(θ1),b(θ2),…,b(θn)]T且θ=(θ1,θ2,…,θn)T，函数b(·)二阶可导.

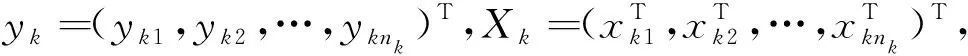
相应地，第k个子块的惩罚估计量为：

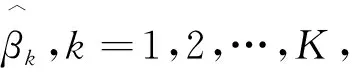
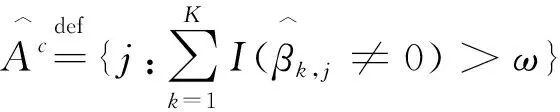
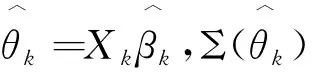
2 抽样法

抽样法基本思想是从初始数据中提取伴随一定概率分布的子样本代替原始大数据对模型进行估计、预测以及统计推断.抽样法的难点在于对各子样本概率分布的设计.下面以经典线性回归模型为例，阐述几种典型的抽样法.

假设y=Xβ+ε，y是n×1向量，X是n×p维矩阵，包含截距项和p-1个解释变量，β是p×1系数向量，ε为服从多元正态分布的残差项，系数向量β的OLS估计量为：

(1)

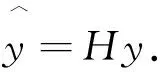
2.1 一般抽样法

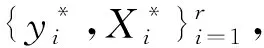
(2)

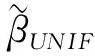
2.2 基本杠杆抽样法

杠杆值抽样法(Basic Leverage Sampling Method(BLSM))基本思想是选取对回归线具有影响的样本点.最初是Weisberg提出杠杆值的概念[11].杠杆值越大，其影响越大.

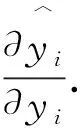
Meng等研究发现当不同维度的数据集具有不同的分布时，BLSM方法将不利于获得高倍影响点.为了克服这个缺点，下面提出缩减杠杆值法.

2.3 缩减杠杆值法

缩减杠杆值法(Shrinkage Leveraging Method (SLM))综合了均匀分布概率法和基本杠杆值得分法，其表达式为这两者的线性组合：

3 在线更新算法

3.1 在线更新一般算法

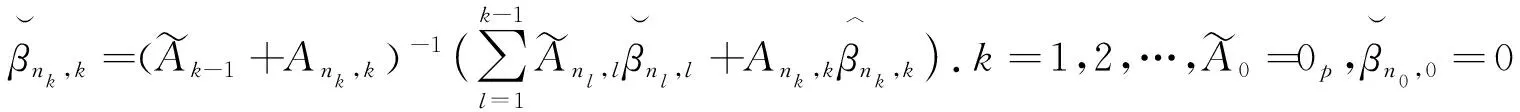
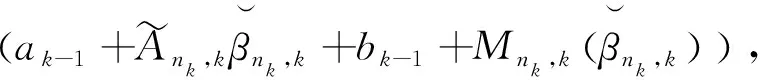
(3)

其中，

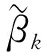
由此可以得到：

利用这个近似关系，式(3)左右两边取方差，得到方差的累积更新估计量为：

(4)

其中，

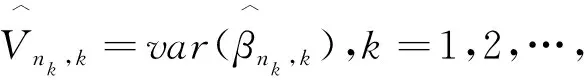
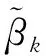
3.2 基于标准变量选择的在线更新估计量

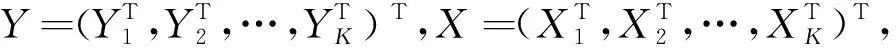
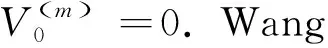
(5)

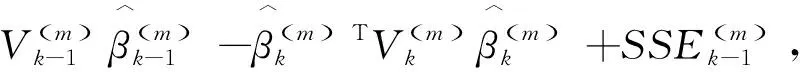
(6)

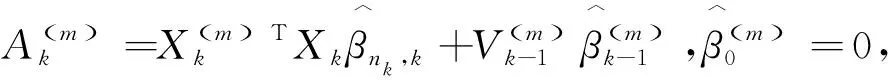
4 研究展望

大数据表现出的高维性、海量性和实时性等特征，为大数据统计分析提出了严峻的挑战.围绕这些挑战，分治算法、抽样法和在线更新算法已经取得重要进展，但鉴于大数据的复杂特征，仍有诸多亟待探索与解决的难题.

(1)模型精确性和计算效率的权衡.在大数据分析中，为了得到更精确的结果，通常不仅需要更复杂的模型，而且需要更多的计算资源，往往造成计算极其复杂，计算成本偏高，计算效率偏低.那么如何在计算精准性和计算效率之间权衡是我们面临的一大问题.这就需要为简单模型设计有效的算法，也即在大数据背景下，使得简单模型具有更加良好的表现.例如，Google公司翻译和语音识别系统，由于大数据的可获性，显著提高了传统经典模型优良精准的特征.这个例子说明传统简单模型在大数据背景下可能具有更精确的表现.那么，如何获得得益于大数据的简单准确模型将是一个巨大的挑战；

(2)排序问题.从海量大数据中筛选出最有价值的信息极其重要.此类统计排序问题目的是将最重要或关联最强的信息排在最前面.一般来说，最重要的信息排列在前，那么该排序算法最好.研究者面临如何设计统计意义上合理的量度，来衡量排序的质量，以及后续的对统计推断的研究(Duchi等[13])；

(3)尾部特征分析.在传统经济学中，概率0.05会被认为是可以忽略的稀有事件.然而，在大数据背景下，这些所谓的稀有事件可能频繁发生，将引起特别的关注.这就意味着尾部行为特征分析也将成为大数据问题的巨大挑战之一；

(4)大规模优化问题.众所周知，在建模中，优化起着至关重要的作用.例如最大似然估计法就是解决优化问题的常规方法.在大数据应用中，一个重要的方向便是在线优化算法.对处理实时更新的大数据流，在线优化算法应具备两个基本特征：1)在线优化算法不仅能减小样本数据的存储量，而且能存储和实时更新模型的估计参数；2)在线优化算法同时兼顾模型拟合和模型选择.比如，当新数据流来临时，模型拟合和模型选择能同时更新吗？模型选择参数能同时发生调整吗？这些是在线优化算法需要考虑的研究课题；

(5)因果推断模型.在大数据背景下，因果推断问题将面临极大的机遇与挑战.主要应用方面有：气候变化问题、医疗健康疗效比较研究以及行为经济学等问题.例如，给定100万人的电子健康记录，我们哪些药品在哪些方面有疗效？目前这些因果推断方面的研究在大数据背景下少有关注.

综合来看，尽管大数据统计分析的研究成果尚处于起步阶段，目前仅仅进行了一些初步探索.但是，围绕海量性、高速性及在线更新实时性等特征的研究文献已经为大数据统计分析提供了一个基本的研究框架，为更多有价值研究的不断涌现奠定了重要基础.

5 总结

本文在对现有大数据统计分析研究文献进行归纳和总结的基础上，具体从分治算法、抽样算法和在线更新算法三方面阐述分析，希望能够为关注大数据统计分析理论与应用的研究者与实践者提供参考.可以预见，在未来的大数据研究中，具有快捷、清晰、高效探测事物内在关系和规律的大数据统计分析领域将涌现出大量的重要研究成果.