252Cf自发裂变中子发射率符合测量的回归分析∗

李永明 王亮 陈想林 阮念寿 赵德山

(中国工程物理研究院材料研究所,绵阳 621907)

(2018年5月31日收到;2018年10月15日收到修改稿)

252Cf同位素源具有标准的自发裂变中子能谱,但由于其半衰期较短,应用中常需要对源强进行标定修正.随着源年龄增加,来自源中250Cf和248Cm自发裂变的影响愈加凸显,不能简单按252Cf的衰变规律计算源中子发射率,而通过锰浴活化的间接测量方法周期较长,且在源强低于104n/s时误差较大.最近,基于中子多重性计数的源强绝对测量算法已得到验证.本文进一步从点模型假设的测量方程出发,在将符合计数率与总中子计数率关联的基础上,分别对符合计数率随源位置、符合门宽的变化关系进行回归分析,提取变化过程的特征系数,建立了两种避规效率变化的252Cf中子发射率测量方法,并基于JCC-51型中子符合测量装置开展实验验证.结果表明:两种回归分析方法的测量值均与标称值的修正结果在2%的偏差范围内一致;反推求得装置中轴线上的探测效率也与基于MCNPX程序的蒙特卡罗模拟计算值相符.研究结果可为活度信息不明的252Cf源强标定及符合测量装置的效率刻度提供便携准确的实验方法.

1 引 言

252Cf源的自发裂变中子能谱已被推荐为国际ISO标准谱[1],广泛应用于中子探测器的效率刻度[2−4]、中子剂量仪器的标定[5,6]、核材料中易裂变核素含量的激发分析[7,8]等科研工作.但由于其半衰期仅有2.645年[9],且随着源年龄增加,来自初始250Cf和其α衰变产物248Cm的自发裂变影响愈加凸显[10,11],不能简单地只按照252Cf的衰变规律计算源中子发射率,使用前常需要对源强进行标定修正.

基于55Mn(n,γ)56Mn反应的锰浴法[12]可间接测量源中子发射率,但为满足较好的统计精度,一般要求源强不低于104n/s且需辐照MnSO4溶液达8 h以上[13].而目前国内具备该类基准设备的单位有限,预约标定将涉及源运输的辐射安保审批,周期较长且费用较大,因此发展更加便携、更大适用动态范围的测量方法具有现实意义.

2013年,Croft和Henzlov[14]基于中子多重符合测量原理,建立了点模型假设条件下源强与总中子计数率S、符合计数率D、三重符合计数率T的四种相互关系,经由121根3He正比计数管组成的高效率中子多重符合测量装置实验验证,测量量分别为S-D,S-T,D-T,S-D-T的求解精度都在2%以内,其中S-D方程的误差最小,其他方法主要受T影响有略大的统计涨落.2014年,国内陈利高等[15]开展了该类测量算法的简化研究,结合中子在系统内的衰减时间行为先求探测效率,再反推源强;并采用由32根3He正比计数管组成的装置对5个不同活度的252Cf镀膜源进行测量,结果与修正标称值的最大相对偏差为1.41%.上述两个工作都是在对系统进行参数优化后,将待测源置于探测器中心开展绝对测量.

若源在测量腔体的不同位置系统探测效率将发生改变,且符合计数率也随符合门宽的增大而增加.但由于入射中子的平均能量相同,其在装置灵敏探测区域内的平均衰减时间近似为一个特征常数,以上过程可认为满足相同的测量方程.另外,近年来数字化分析设备已逐步替代移位寄存分析器用于处理中子响应的脉冲时间序列[16],可实现一次测量后加载不同状态参数的离线反演.由此可探索更为灵活普适的252Cf源强测量方法.

本文从核材料中子被动符合测量方程出发,在约化探测效率的基础上,考察不同源测量位置、不同符合门宽对计数率的影响,通过回归分析提取变化过程的相同特征系数,进而求解252Cf源自发裂变的中子发射率,并开展相关的实验和蒙特卡罗(MC)模拟验证工作.

2 理论分析

对基于3He阵列的中子符合测量装置,在将待测样品的空间分布认为是点源,且假设(α,n)反应中子与自发裂变中子具有相同的能量分布和探测效率的条件下,核材料自发裂变中子的被动符合测量方程可表达为[17]

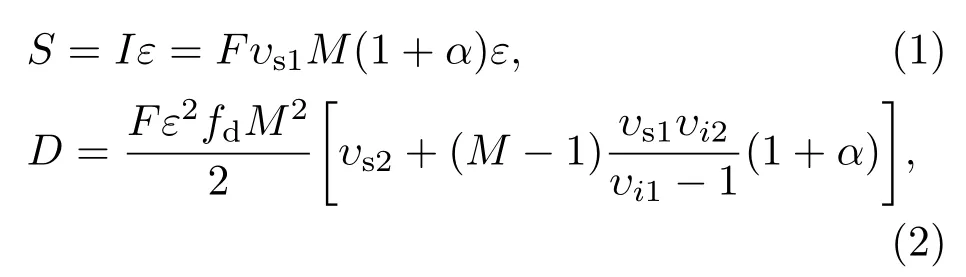
式中,S为总中子计数率,I是核材料的中子发射率,ε是系统平均中子探测效率,F是核材料的自发裂变率,M是中子在待测样品中的增殖系数,α是核材料(α,n)反应中子与自发裂变中子的比值,D为符合中子计数率,νsj是自发裂变中子多重性分布的j阶矩,νij是诱发裂变中子多重性分布的j阶矩,fd是双重符合门宽的利用率:

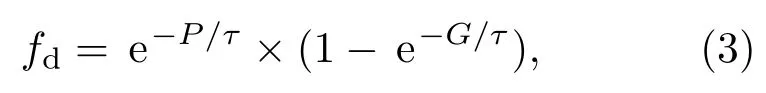
其中,P为预延迟时间,G为符合门宽,τ为中子在装置中的平均衰减时间常数.

从(1)和(2)式可知,系统探测效率的改变将对D值和S值均产生影响,由此经数学变换可约掉效率,即把符合计数率D由总中子计数率S进行展开:

对不锈钢封焊的小体积252Cf点源,源材料与18O,13C等核素发生(α,n)反应以及诱发裂变等中子增值因素可忽略不计,可取α=0,M=1,则(4)式进一步简化为

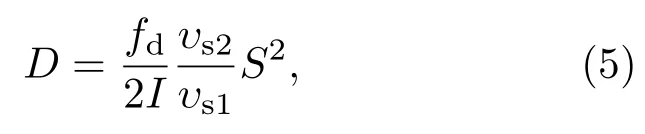
其中,自发裂变中子多重性分布的一阶矩和二阶矩分别为υs1=3.757;υs2=11.962[17].

2.1 不同符合门宽的源强回归分析

由(3)和(5)式可知,在测量位置及预延迟固定的情况下,系统fd值和符合计数率均随着符合门宽的增大而增加,但过程中总中子计数率S不受影响,可认为是个不变量,此时(5)式可进一步简化为线性关系.设K1为D随fd的变化斜率,可由最小二乘拟合的回归分析求出,则252Cf源的中子发射率可表达为

2.2 不同源位置的源强回归分析

在系统预延迟时间、符合门宽固定,即fd值为常数的情况下,随着源在测量系统的位置不同,符合计数率随总中子计数率呈抛物线的变化规律.设K2为D随S2变化的斜率,可由最小二乘拟合的回归分析求出,则252Cf源的中子发射率表达为

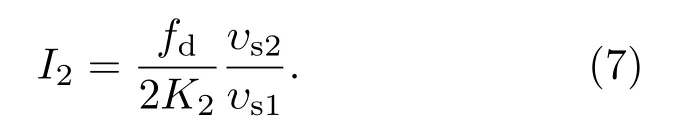
3 实验测量

本文基于JCC-51型中子多重符合测量装置[18]开展验证工作,系统组成及原理流程如图1所示.该装置由42根长度为50 cm、气压为4 atm(1 atm=1.01325×105Pa)的3He正比计数管分两环内嵌于高密度聚乙烯组成,测量腔体内径为22.9 cm、外径为47.8 cm.探测器工作高压为+1680 V,前置放大器的输出信号由数字化分析器MCA527[19]获取,对中子响应的脉冲序列按照列表模式(list mode)进行标记和存储.可统计出中子在测量装置内的符合计数随时间的衰减分布曲线;加载预延迟时间、符合门宽、延迟时间等参数进行离线反演,可得到总中子计数率、符合计数率和长延迟后的偶然符合计数率,将符合计数率减去偶然符合计数率便得到真符合计数率;考虑死时间修正后可获得源中子在探测器内的多重性分布.待测的小体积252Cf中子源由美国橡树岭国家实验室生产封装,活性区直径和高度均为1.57 mm,2003年11月25日出厂时总活度为4.255×105Bq,其中250Cf占总活度的3.64%,252Cf占总活度的96.31%.

根据装置说明,固化预延迟时间为4.5µs,延迟时间为1000µs.另外还需对符合门宽进行优化选取,设置过小则符合计数率太低而失去统计意义,过大则偶然符合计数较多,导致真符合计数将是大数减大数的结果.这里先将源置于系统中心,重复3次300 s的测量,将符合门宽从16µs到160µs依次步进调节进行数据反演,步长为16µs,考察不同门宽及其利用率对符合计数的影响.随后固定一个优化符合门宽,将源沿着探测器中心轴向从距顶部5.0 cm的位置向底部平移,每次步进5.0 cm后重复3次300 s测量,考察不同探测效率下符合计数率D和总中子计数S的变化关系.

图1 实验系统及设置Fig.1.Experimental system and set-up.

4 结果与讨论

具有时间关联特性的源自发裂变中子在装置中被聚乙烯慢化,以其中一个中子被3He俘获形成的脉冲作为符合触发信号,系统在之后t时刻相邻dt间隔内测到中子数N(t)的分布如图2所示,满足指数衰减的Rossi-α分布规律[17]:

式中A为随机符合计数率,R为真符合相关的计数率.取dt=1µs,可拟合出中子在装置中的平均衰减时间常数τ=51.887µs±0.27µs,按(3)式可近一步求出不同条件对应的符合门宽利用率fd.由于预延迟时间P与符合门宽G是精确给定的反演参数,可忽略其不确定性,则fd的标准误差可由下式求出:

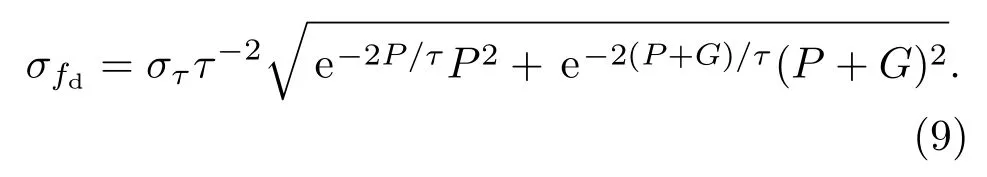
图2 252Cf源位于装置中心的中子Rossi-α分布Fig.2.Neutron Rossi-α distribution as252Cf source in the central of counter.

当源置于探测装置中心,反演得到如图3(a)所示的符合计数率D随符合门宽利用率fd的变化趋势,两者近似满足线性关系,在测量时间tm内,总中子计数率S不变,其和D的标准误差分别为

由于系统稳定性较好,在300 s内测量到足够的统计计数,σS和σD值相对较小,对D-fd关系进行带误差的最小二乘拟合,可得斜率K1=176.133±0.090,按(6)式求得源中子发射率I1,其对应的标准误差为

结果为I1=(1202.1±7.3)n/s.

将符合门宽设定为64µs,反演252Cf源置于腔体中轴线不同位置的符合计数率随总中子计数率平方的变化关系,结果如图3(b)所示,也近似呈线性,对D-S2数据进行带误差的最小二乘拟合可得到斜率K2=8.524×10−4±0.029×10−4,进而按(7)式求得源中子发射率为I2,其标准误差如下式计算:

结果为I2=(1213.7±5.5)n/s.

上述实验于2017年12月27日开展并完成,根据半衰期、自发裂变分支比(T1/2250Cf=13.08年,F250Cf=7.7×10−4;T1/2252Cf=2.645年,F252Cf=3.092×10−2)[9]等参数对源强的出厂标称值进行修正计算,结果为1225.9 n/s,与两种回归分析的测量值在2%的偏差范围内相符.

求出源中子发射率后,由(1)式可得到装置中轴线上不同位置的探测效率ε,其标准误差可由下式求出:

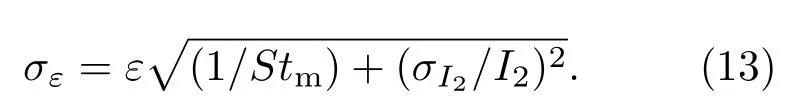
另外,基于MCNPX[20]软件对测量装置进行几何建模和MC计算,跟踪106个252Cf自发裂变中子,其出射能谱选取为瓦特分布(参数a=1.18 MeV,b=1.03419/MeV),通过统计3He(n,p)3H俘获反应事件数获得不同源位的系统探测效率.图4展示了模拟结果与实验值的比较情况.当源位于装置底部时,中子与底座材料发生相互作用的概率增加,S的测量值中包含了部分随机散射中子的贡献,导致实验获得的效率略高于MC计算值,除此之外的大部分灵敏测量区域内两者均符合得很好,也进一步验证了该分析方法的准确性.

图3 中子符合计数率的回归分析 (a)不同的符合门宽;(b)不同的源位置Fig.3. Regression analysis of the neutron coincidence counting rate:(a)Different coincidence gates;(b)source at different positions.

图4 252Cf源在装置中轴线不同位置的探测效率Fig.4.Neutron detection efficiency of system as252Cf source at the central axis.

5 结 论

本文建立了两种不依赖于效率的252Cf源强回归分析方法.当源固定在测量腔内合适的位置时,通过一次测量后进行多个符合门宽等参数的离线反演,在保障数据的一致性的同时提高了测量的便携性;当源固定在一优化的符合门宽时,可在灵敏体积内开展较大动态范围的测量,也有效地降低了对源位的置放精度要求.采用出厂中子强度已知的小体积252Cf源与JCC-51型中子符合测量装置进行实验验证,源中子发射率测量值与标称值按半衰期修正的结果在2%的误差内一致,获得装置中轴线上不同位置的探测效率也与MCNPX程序的MC模拟结果相符,表明该技术方法是行之有效的.其可应用于新购或未知源强的核对标定;也可在未知源强度的条件下开展符合测量系统的效率刻度,减少了对标准源的依赖.

值得指出的是,随着源经历时间的增加,来自250Cf自发裂变的影响将逐步增强[10,11],采用本方法对大于20年以上的老源进行测量时,需要先求解初始250Cf与252Cf的活度比值,再对多重性分布参数进行权重的修正.