整合公路运输服务下竞争性港口定价博弈模型

王文渊，王盛华，彭 云，徐星璐

(1.大连理工大学水利工程学院，辽宁大连116024；2.广州港集团有限公司，广州510100)

0 引言

在激烈的市场竞争环境下，港口物流竞争已涉及到整个供应链[1].如何提出合理的长期竞争策略(投资策略、服务差异化策略)和短期竞争策略(定价、产量)来应对港口竞争，提升企业地位成为港口管理者关心的重要课题[2].差异化的服务和合理的定价有助于港口吸引货源，提高区域内的自身竞争力.其中，港口整合公路运输服务，实现“门到门”物流服务，已成为部分港口制定差异化服务策略的重要备选战略.然而定量分析整合服务为企业带来的效益，必须考虑区域内港口竞争，制定合理的服务整合路径决策和定价决策.

博弈论能够处理有关港口经济各方面的问题，同时它还使得从理论上分析港口管理的决策对于港口利润、港口竞争中所处的地位和社会福利等的影响成为可能[2].对此，大部分有关港口竞争策略的研究问题都是基于博弈论对差异化策略进行定价博弈来观察竞争策略的实施效果.Álvarez-SanJaime等[3]基于一维港口定价博弈模型，得出港口整合运输服务的利润变化情况；Zhang等[4]建立港口竞争博弈模型研究港口的多式联运网络规划和定价策略优化问题；Zhuang等[5]建立了Stackelberg寡占模型来研究港口集装箱及干散货差异化服务博弈.港口企业的竞争直接结果之一是各方市场份额的变化，与市场份额竞争相关的研究主要以效用理论作为研究基础，并通过MNL(Multinomial Logit)模型来进行表达用户的选择[6-7].

港口服务定价博弈研究大多关注港口企业对一维线性或二维平面空间上的连续型腹地的竞争，研究方法多使用公式推导进行均衡求解，而实际中的物流网络往往由各级交通枢纽节点及其线路交织连接而成，故用离散网络节点来表示腹地用户空间关系更为合理.对此，本文对空间离散网络节点中的港口整合服务策略进行研究，通过MNL模型表达不同服务的市场份额，考虑整合公路服务路径及定价策略两个因素，构建非合作双寡头定价博弈模型，并通过数值算法求解Nash均衡.

1 问题描述

两港口(A、B)位于网络节点的两端，对分布在其中的腹地节点进行竞争，如图1所示.初始的港口服务均衡价格分别为PA0、PB0，港口单位货物服务成本为h.根据MNL模型，用户对运输服务的选择遵循效用最大原则[8].用户对货物运费、运输时效、服务可靠性等因素的偏好，体现为用户的货物运输效用.货物运输效用函数由效用的确定项和随机项组成，在本文中，效用的确定项是单位港口服务费用P及单位公路运输费用c的函数；效用的随机项是用户选择偏好的非直接观察因素，服从一定的概率分布.

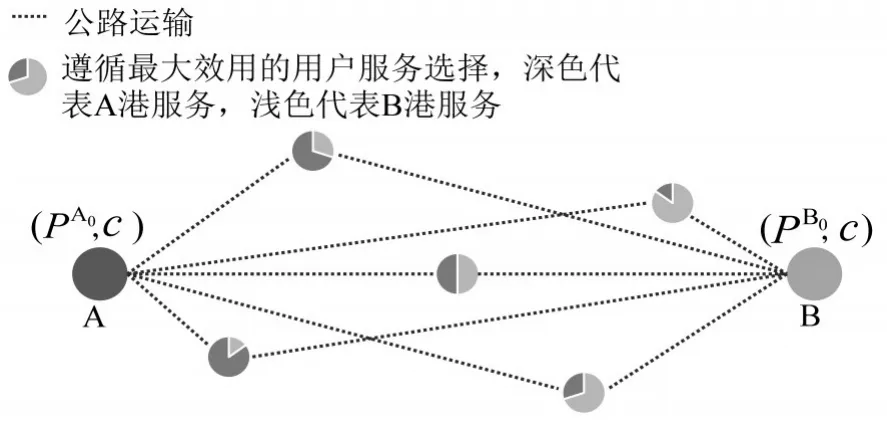
图1 用户服务选择示意图Fig.1 Choice behavior of port services

为更好地分析新服务对竞争双方及用户带来的影响，维持港口B原有服务不变，港口A提出整合公路运输服务的港口服务，并且与原有港口服务相独立，用户根据成本选择服务.新的港口服务价格为PA′，公路运输费用为cA′.港口 A 的可选策略包括服务路径选择策略及价格策略，港口B为价格策略.

2 整合公路运输服务下的港口定价博弈模型

2.1 基本假设

(1)两港口除了所处位置不同，其他方面参数完全相同，包括设施设备水平、通过能力等；

(2)两港口能够满足腹地客户的所有服务需求；

(3)不考虑腹地的铁路运输；

(4)网络中的腹地被完全覆盖；

(5)腹地用户效用随机项是独立同分布随机变量，符合二重指数分布(Gumbel Distribution)且均值为0；

(6)全部参与者具备完全信息.

2.2 腹地用户选择模型

用户选择各港口服务的货物运输效用使用MNL模型进行计算，公式为

用户货物运输效用的确定项为用户运输单位货物的最大支付意愿扣除成本所得的净效用，即

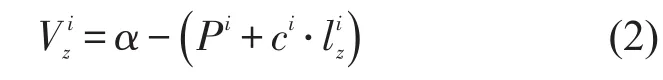
式中：α为运输单位货物的最大支付意愿，设该值足够大以保证效用始终大于0；Pi为单位货物选择服务i在相应港口产生的全部费用；ci为单位货物选择服务i所产生的公路运输费用；为用户z与提供服务i的港口之间的距离.

货物运输效用的随机项则根据服务可靠性、运输方式便利程度等非直接观察因素产生变化.当服从二重指数分布且均值为0时，MNL模型变形为Logit离散选择模型，具体公式为

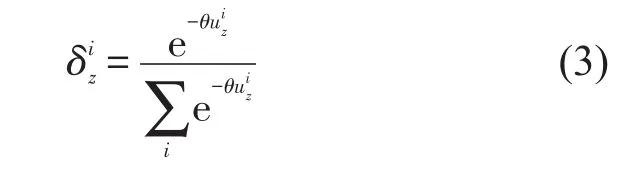
2.3 港口定价双层规划博弈模型

港口企业运营成本分为固定成本及变动成本，港口的策略选择以利润为主导因素，并通过均衡价格体现博弈的结果.整合公路运输服务情况下的港口定价双层规划博弈模型由上层模型——港口A利润最大化函数，以及下层模型——港口B利润最大化函数两部分组成，上层模型将价格决策变量PA、PA′、cA′及路径决策变量oz传递至下层模型，下层模型将价格决策变量PB传递至上层模型，变量说明如表1和表2所示，具体公式为

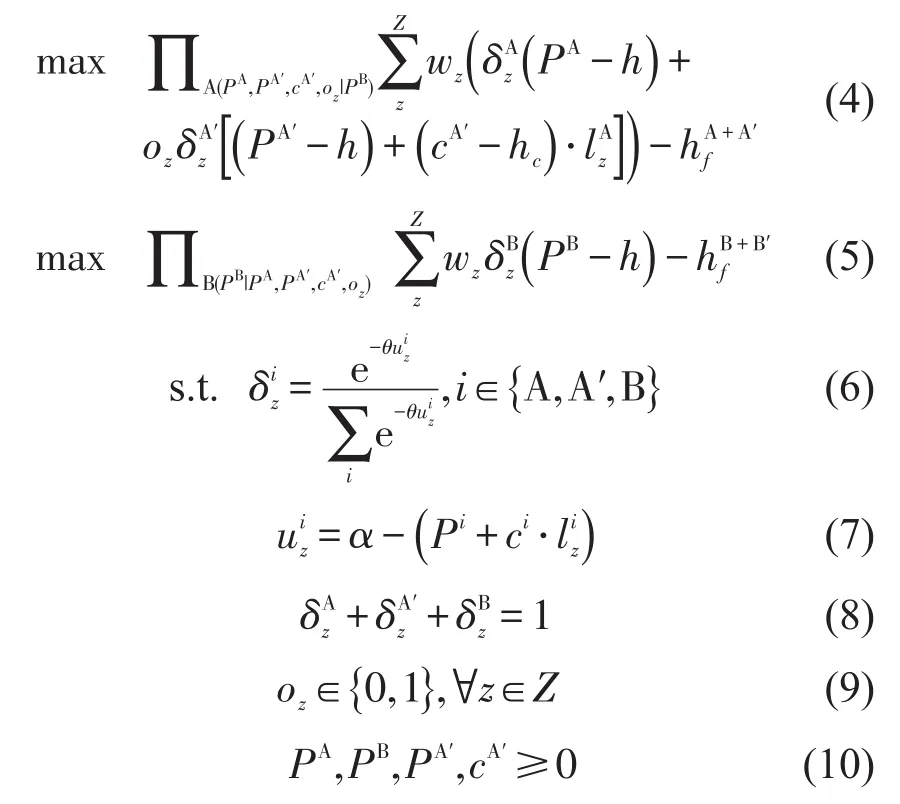
2.4 模型求解

由于网络节点数量的有限性及价格区间具有一定的范围，港口企业的决策空间也是有限的，因此能通过数值算法方便地进行求解.Grauberger[9]提出了在考虑对手策略的基础上进行最优决策，并通过屏蔽等价结果避免非均衡导致程序死循环的近似Nash算法.本文在此基础上对其进行了改进，使之能应用于港口服务拓展的定价博弈问题中.

表1 参数说明Table 1 Parameters of the model

2.4.1 用户选择

所有腹地节点用户选择通过MNL模型计算子模块对A、B港的各种服务参数进行计算，并用变量进行统计，输出到双层规划博弈模型求解程序中.

2.4.2 港口企业决策

港口双方根据对方策略依次交替使用港口定价双层规划博弈模型进行最优策略求解.多次迭代后若当前港口最优决策及利润重复出现时，作如下判断：

(1)最优决策及利润与上一次迭代相同，即企业在两轮决策过程中选择同一策略且利润相同，此策略为Nash均衡策略.

(2)最优决策及利润与上一次迭代之前的港口最优决策及利润相同，则计算过程陷入循环，不存在Nash均衡.

计算求解流程如图2所示.

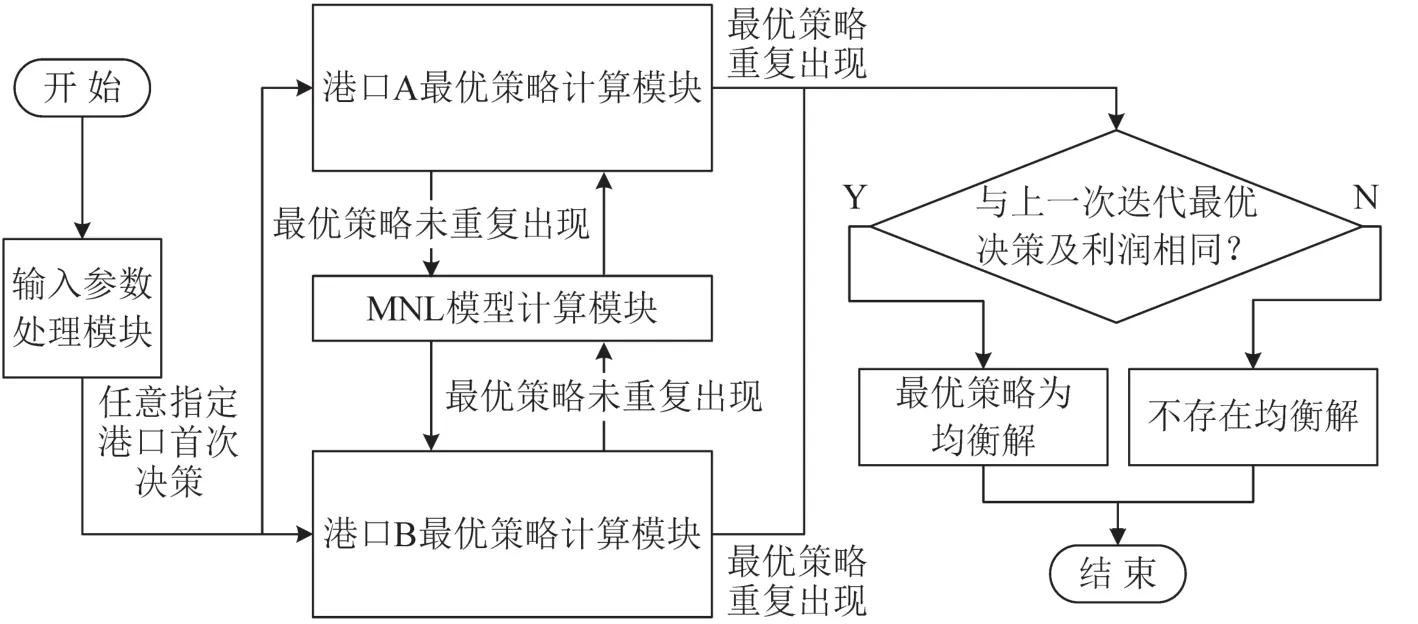
图2 模型求解流程Fig.2 Flow chart of model solution

3 整合公路运输服务下港口定价博弈分析

为计算开通整合公路服务后港口的最优均衡价格及对竞争对手、腹地用户的影响，以某A、B两港区为例，港口双方形成双寡头对其之间的腹地进行竞争，腹地节点数量为10个，根据实地调研结果及程序试算，将用户选择偏好系数θ设为0.016，各腹地基本参数如表3所示，腹地节点示意图如图3所示.

表3 腹地基本参数Table 3 Basic parameters of hinterlands

3.1 初始港口利润分配

表4 初始港口服务市场份额Table 4 Origin market share of port services (%)

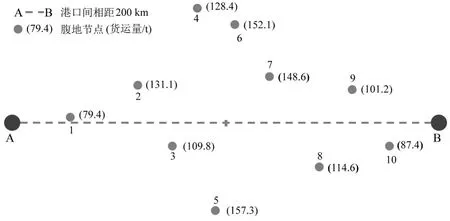
图3 腹地节点示意图Fig.3 Network nodes of hinterlands

由表4可知，初始条件下港口双方各自对己方腹地拥有优势，总体市场份额基本相当，同时对于对方腹地也有一定占比.根据式(4)和式(5)计算得总利润∏A0=247 944.4元，∏B0=236 051.6元，维持在同等水平.

3.2 整合公路运输服务定价博弈

在初始均衡价格的基础上，进一步计算开通整合公路服务情况下的均衡价格及最大利润.各服务价格参数如表5所示.

将均衡求解算法用C++语言进行编写，输入表3和表5中的初始数据进行计算，得出整合公路运输服务下港口均衡价格，如表6所示.

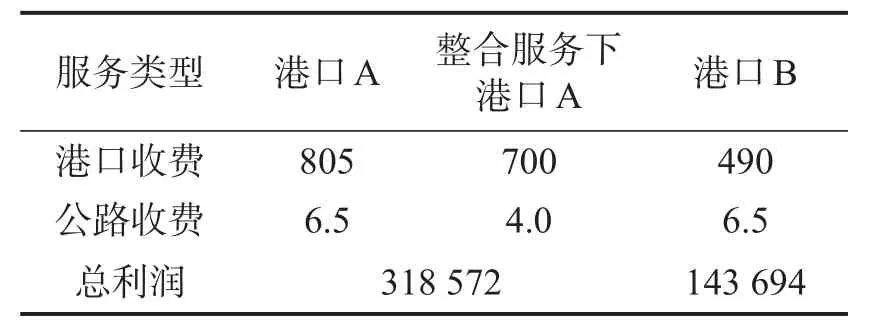
表6 整合公路运输服务下港口博弈均衡价格Table 6 Final equilibrium price of port considering integrated highway transportation service(元)

均衡条件下各腹地市场份额如表7所示.

将表7中的均衡结果及未开通整合公路运输服务的初始均衡进行对比分析，港口A开通了{3,4,5,6,7,8,9}等腹地节点的整合公路运输服务.与之对应，普通服务下港口A收费提高了34.2%，港口B收费则降低了18.3%.整合公路运输服务下的港口收费为较初始均衡价格高出18.2%，提供的公路运输费用则降至设定值下限4元，比公路运输服务成本低1元.港口双方的总利润：∏A=318 572元、∏B=143 694元，港口A利润上涨28.5%，港口B利润下降39.1%.

表7 整合公路运输服务下各港口服务市场份额Table 7 Final market share of port services considering integrated highway transportation service(%)

对比表4和表7可以发现，开通整合公路服务情况下，尽管公路收费低于成本，但港口A的普通服务相较于港口B存在价差优势，定价策略更为丰富，有效增加了中间腹地对整合服务的选择倾向，提高了港口A在中间腹地的总体市场份额，而未选择开通整合服务的腹地节点，与港口B距离较远，用户选择对公路运输费用不太敏感，港口A因此采取高价措施，即使在腹地节点2处市场份额有所下降，总体仍能维持绝对优势.在此定价策略下最后得到的总利润覆盖了亏损的公路运输服务，获得了28.5%的利润提升.而港口B在竞争港口开通整合服务的情况下，公路运输价格存在劣势，中间腹地市场份额下降明显，迫使港口收费下调，利润也随之大幅降低.

3.3 用户选择偏好系数敏感性分析

保持初始输入参数不变，θ取0.004～0.024，步长为0.002，将θ依次输入到求解程序MNL计算子模块中，运行程序进行求解，以观察用户偏好对均衡价格的影响，如图4所示.

对图4进行分析，随着θ增大，各港口服务价格趋低，下降的速率也逐渐降低.在此实例中，θ＞0.018后实例不存在均衡解，是由于用户选择偏好系数越大，随机效用的作用越小，用户对固定成本的变化越敏感，用户的选择偏好将更取决于整体服务成本的大小.此时市场价格竞争将加剧，港口双方都会通过价格下调来抢占市场份额.港口A的两种服务价格同比港口B服务价格的下降速率和幅度都要小，因为通过公路运输的低廉费用，港口A的定价策略自由度更大且优势更高，利润下跌到一定程度才会采取降价措施.同时，整合公路运输服务的价格下降速率比港口服务价格的下降速率快，在θ=0.008时已达到了设定的下限，可见整合公路运输服务的定价策略作用较为关键，在此实例中的优先程度高于港口服务定价策略，并有进一步下调的趋势.

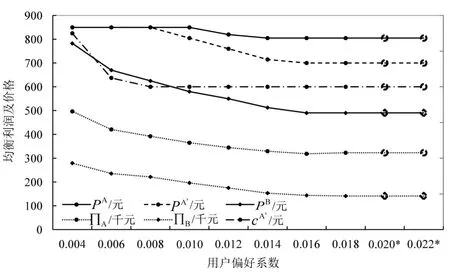
图4 不同偏好系数下的均衡结果Fig.4 Equilibriums of different user preference factor

4 结 论

本文研究了整合公路运输服务情况下竞争性港口的定价博弈问题，通过建立节点网络来模拟腹地与港口的空间关系，并运用Multinomial Logit模型表达腹地用户的运量分配比例选择，从博弈的角度讨论港口双方的最优策略选择.最后通过算例的求解和用户选择偏好系数敏感性分析，得出以下结论：

(1)港口企业进行整合公路运输服务能增加港口定价自由度，通过降低公路运输费用，能有效增加竞争港口双方中间腹地的市场份额，在实现服务升级的同时增强港口竞争力.而对于与港口相邻的己方腹地，由于其对公路运输费用不敏感的性质，将不开通整合服务，并借助整合服务获得的优势提高港口服务收费，通过两种服务的联合定价策略全面提升港口利润.

(2)MNL模型中的用户选择偏好系数θ指示了市场竞争的激烈程度，对均衡价格的影响较为显著，在实际的市场竞争中，用户对服务成本的倾向越大，则用户选择偏好系数越大，用户的选择将由成本主导，市场竞争激烈程度会进一步加剧，港口双方都会采用降价的措施来实现利润最大化，最优均衡价格也会降低.

(3)港口服务拓展是港口企业的重点发展方向之一，本文只对港口服务中的公路运输服务进行了研究，而其他港口服务也同样具有较高的研究价值，如铁路运输服务、海公铁联运服务等问题都有待进一步的研究.