回归传统:当代数字化建筑几何建构策略研究
Chen Zhonggao Ji Guohua
建筑学自产生以来便与几何学密不可分,在数字技术的推动下,几何学在建筑学中的地位正在发生改变。从2005年布兰科·克拉列维奇(Branko Kolarevic)提出数字化设计是几何关联的定义过程,[1]到2010年托尼·科特尼克(Toni Kotnik)将数字化设计概括为几何“图灵机”(Turingmachines)的操作,[2]再到2013年阿希姆·门格斯(Achim Menges)提出几何学是无缝链接运算系统与物理系统的中介,[3]可以看到,伴随着数字技术的发展,正出现一种以几何学作为普遍命题与建筑学建立关联的趋势。在这一背景下,几何学与建筑学的关联性则需被重新审视。基于此,本文试图从操作层面简要梳理建筑学和几何学两者关系的发展历程,重点是基于案例来阐述当代数字化建筑的几何建构策略,并将之置于完整的历史背景中进行讨论,我们会发现,数字时代的几何学是一项正在进行的传统回归,依赖于数字技术,它能够为复杂建筑形体的生成、分析和建造提供实践可能性,以期重拾几何触发建筑学的创造力。
一、传统的消失
公元前4世纪的雅典娜神庙应该是最早应用几何规则设计的建筑,其平面和结构元素都从方格网中发展而来。[4]至中世纪,得益于几何学,当时石匠们普遍采用一种称为切石术(Stereotomy)的几何操作来指导石材设计与加工,这一种平行投影方法,能够在真实建造前建构出建筑各组成部分的三维形态和精确比例,而无需现场进行设计与度量。1567年,法国建筑师菲利贝尔 · 德洛姆(Philibert Delorme)在《建筑要典》(LePremier Tome de l’Architecture)中 对 这 一操作进行详细阐述,[5]他强调其从原理到技巧各个层面支撑着建筑系统的内在逻辑(图1)。文艺复兴时期,阿尔伯蒂(Battista Alberti)继承并发扬了维特鲁威(Marcus Vitruvius)的古典柱式体系,进一步提出比例系统作为建筑设计的普遍原则。事实上,这一原则是一套系统化的几何方法,利用直尺和圆规,建筑师通过基于线段切分的几何操作来完成建筑从设计到建造的全过程。[6]之后,在伯鲁乃列斯基(Filippo Brunelleschi)、阿尔伯蒂等建筑师的透视学研究基础上,画家皮耶罗·德拉·弗朗西斯卡(Piero della Francesca)将几何学引入到透视学中,并以此为起点促进了射影几何、画法几何等几何学的发展。[7]这时期,建筑学以几何学为设计基础,两者是相互依赖和彼此促进的。因此,从中世纪到文艺复兴,几何规则与实体建筑的逻辑关系是直接的,无需思维的转换。立足于几何操作,建筑师确立建筑真实建造的几何形态和建造逻辑。此时,作为设计思维的几何学不仅指导建筑设计的全过程,同时为建造施工提供思路和方法,使得建筑成为可控的整体系统。

图1:菲利贝尔 · 德洛姆对拱形切石术的几何特征图解
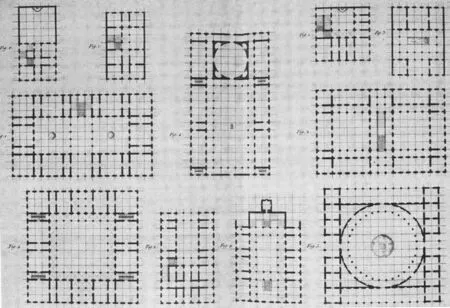
图2:路易斯 · 迪朗对基于网格设计的院落图示
1570年,伴随着印刷术的影响,帕拉第奥(Andrea Palladio)在《建筑四书》中已采用纯数字计算的方式来阐释有关柱式的比例关系,[8]表明建筑学开始出现从几何学往代数学转变的迹象。17世纪科学革命时期,建筑设计过程中关系的量化需求导致几何学不断丧失地位。至19世纪初,任教于巴黎综合工科学院的法国建筑师路易斯·迪朗(Louis Durand),将与画法几何相关的正交投影和模数化网格引入到建筑学中[9](图2),这促使几何学的重要性理解转向于为了完成设计而采用的工具,从而丧失本身所具有的创造属性。同时,他把几何学建立在满足功能需求的基础之上,将之建筑类型化。这一切促使建筑学开始疏离于几何学,使其实质成为建筑制图的辅助性工具,并一直影响着现代意义上的建筑学直到今天。现代建筑阶段,画法几何已不是建筑学必修的专业训练之一,[10]同时,建筑师也不再像文艺复兴时期的前辈们主动关注几何学,他们已习惯于几何学作为单纯技术的思维模式,同时满足于欧式几何的建筑应用,从而远离微分几何、拓扑几何等复杂几何学带来对建筑学理解的新可能性,进而导致了建筑学科的知识远滞后于几何学发展。一直到数字时代,几何学传统的消失,使其仅作为隐藏建筑学背后的绘制和表现工具,成为“死的几何学”。[11]
二、探索与转型
20 世纪初期,以安东尼奥 · 高迪(Antoni Gaudi)、巴克敏斯特·富勒(Buckminster Fuller)和费雷·奥托(Frei Otto)为代表的设计者致力于几何形式和力学性能的一致性研究,创造出网格结构和薄壳结构的建筑形式(图3)。其中,高迪开创出直纹面的建筑形式语言,在他设计的圣家族大教堂中,建筑形式完全采用直纹面构成,[12]这种曲面由按照一定轨迹运动的直线形成,因此便于施工者支模建造。柯布西耶(Le Corbusier)通过与数学家雅尼斯·泽纳基斯(Lannis Xenakis)的合作,[13]在朗香教堂和布鲁塞尔世博会58号展馆的设计中,同样采用这类曲面来控制建筑形体和建造施工。此外,奥托利用肥皂沫实验获得极小曲面的几何形式,并将之付诸于建筑轻型结构的实践。当时,这种通过几何规则与建筑结构、施工建造等建筑逻辑寻求一致性的设计方法,为以功能至上的现代建筑提供了更多的设计可能性。然而,这时期的探索存在着其时代局限性:一方面,此类建筑设计大都源于工程师和数学家,而建筑师很少去关注几何学建构的建筑形式创新;另一方面,受限于当时的计算技术,此类设计方法有着不确定性,因而无法在建筑实践中普遍应用。
20世纪90年代的 第一次数字转型(Digital Turn)[14]则是建筑形式的新几何学探索。一方面,从复杂科学引进的不连续性、递归性及自相似性被建筑师作为设计策略的理论基础,引发了建筑形式的转变;另一方面,随着计算机辅助设计的发展,光滑的样条曲线在建筑形式上得到普遍应用。基于这两方面原因,自由曲面迅速成为时髦的建筑形式语言,甚至一时成为数字化建筑的标签,这一时期的建筑师以格雷戈·林恩(Greg Lynn)、弗兰克·盖里(Franke Gehry)和扎哈·哈迪德(Zaha Hadid)为代表(图4)。但是,由于建筑师无需了解隐藏设计背后的几何规则,而是根据直觉判断和美学认知来完成建筑形体的产生,建筑无法与客观环境或真实建造取得关联,只是在计算机虚拟空间中实现其复杂外形的精确描述。因此,此时新几何学仅仅是作用于建筑表皮,并未推进几何学与建筑学两者的实质关系,从而引发建筑设计中几何思维的转变。
三、当代数字化建筑几何建构策略
当前,数字化技术与建筑学的结合正不断改变和拓展着建筑设计思维,随着算法设计、性能化设计等新方法的不断出现,复杂建筑形体作为理性数据和感性审美互动的输出结果,极大地丰富了建筑设计内容。面对这一设计条件,建筑师逐渐认识到传统的几何思维已无法有效处理设计建造中衍生的问题,进而转向于寻求一种与建筑逻辑协调的数字化几何建构思维。下文试图在当前纷繁的数字化建筑设计中归纳出几何建构的4种策略:几何生形、几何转化、协同模拟和几何重构,并通过分析具有代表性的案例来阐述其内容。

图4:20世纪90年代数字转型期的代表建筑师及作品

图5:利用极小曲面组织空间的台中大都会歌剧院

图6:哈萨克斯坦新国家图书馆的莫比乌斯环外形(左)和剖面示意(右)
1.几何生形
基于几何算法的建筑生形是数字时代建筑学与几何学建立联系的最直接方式,在计算机中输入几何算法的参数方程,把生成的图形作为建筑形体的雏形,并以此为起点开始进一步的深化设计,例如几何镶嵌、泰森多边形、分形几何等算法常作为建筑形式的设计选择。
建筑师伊东丰雄设计的台中大都会歌剧院(2014)是利用三周期极小曲面作为空间构成单元的建筑案例(图5),整座建筑的墙、柱、楼板彼此形态相连,打破了传统水平楼板划分的分层式空间,营造出持续生长的空间效果。基于建筑师的腔体设计理念,在超过5万m2的剧院综合体内,只采用一种几何秩序来组织形态,进而呈现出新的建筑有机形式。同时,极小曲面的几何规则确保了建筑的高结构性能,不仅可作为分隔界面,同时是承重体系,为寻找空间形态和结构合理的设计过程提供了有力的逻辑。
在哈萨克斯坦新国家图书馆方案竞赛中,丹麦BIG建筑事务所的设计作品(2009)成为最终方案被选定(图6)。整个方案外形为莫比乌斯环,包含两个相互咬合的组成单元—— 规整的圆形和盘旋的立体空间,从而用一个连续的表面将图书馆、博物馆和服务功能等空间组合的变化包裹在内,这种方式下各空间不再是传统的水平毗邻排列,而是转变为各种功能相互叠落的方式,从而通过不同方向的拓展,塑造出一个高度契合建筑功能需求的动态循环空间。
在数字化转型时期,由于输入的几何算法并未考虑任何建筑相关信息,因此往往集中于生成图形化的建筑形体,这也是其被批判的原因之一。作为这一问题的回应,当前,在基于几何算法的建筑生形过程中,更多的是在设计初期即建立几何形体与功能需求的关联,或是利用可建造的几何规则生成建筑形体,以此作为数字化建筑建构的一种出发点。
2.几何转化
近年来,随着数字技术的发展,生物内部的复杂几何结构能够被观察、挖掘和转译。受此启发,建筑仿生设计从早期生物形态的单纯模仿开始趋向于生物几何系统的建筑转化。生物几何系统不仅呈现生物的形态特征,同时包括生物内在结构的组织关系,可以转化为更合理的建筑形式。
斯图加特大学计算机运算所(ICD)从2013年开始进行连续的建筑仿生研究和实践。在2016年的展亭设计中(图7),他们首先通过对海胆结构的观察,总结其双层结构、单元之间纤维连接、壳体开放、壁厚不均匀等几何系统特征,并基于这一特征,决定展亭的结构形态、连接方式和材料分布。最后完成的展亭整体为开放壳体形式,采用双层木板单元组合而成,材料厚度为3~ 6mm的不均匀分布。同时,相邻单元模拟海胆的连接方式,利用碳纤维进行编织而完全不需要金属连接件。这一构筑物跨度达到9.3m,重量为780kg,清晰地展示了生物几何系统转化为建筑轻型结构的巨大潜力。
英国建筑联盟学院(AA School)在2016年基于树木的自然分支系统探索了建筑大跨结构的设计可能性(图8)。这一设计流程可分为:1)利用三维扫描多种适当的树形,构建出有效的几何系统数据库;2)逐个分析分枝结构的分支角度、最小直径;3)选择最优生长的分支结构形态,在计算机中用网格曲面近似模拟;4)建立精准的几何参考系统,确保组件的位置和相互关系,从而与建造对接。最终建成的拱形桁架跨度为25m,由20根树木分支组成,并且在建造大跨结构的同时保证用料浪费最少。
有别于传统的仿生建筑设计,生物几何系统的建筑转化更加关注从形式到建造各个环节的对应关系,以此决定建筑材料、节点和建造方式直至最终的形式呈现。在这过程中,选用什么样的几何特征以及如何转化为建筑语言,需要建筑师对生物的几何特点进行深入分析,并对相关的生物学范畴有一定了解,才能生成合理性和创新性兼具的建筑形式。
3.协同模拟
借助计算机技术,几何形式自身可作为建筑设计对象进行衍生和操作。在这一策略中,基于物质性能和几何属性双向互动的制约关系,模拟两者融合的动态过程,这样就形成了几何协同建筑性能的设计找形方法,为建筑设计带来了新的内容。
斯图加特大学联合研究团队在2011年公共展亭的建造中(图9),基于有限元分析,将力学性能融入构筑物形体的计算性生成中。设计师首先导入预先设定的单元形状,然后由计算机程序根据结构静荷载和预应力,自动生成最终稳定的三维构筑模型。在这过程中,单元形态是动态的,趋向于整体结构稳定的同时,结构性能赋予其精确的几何参数,从而生成不规则的六边形单元。该设计的重要意义在于把几何形态与力学设计目标融合,直观地展示了几何协同的模拟找形过程。
诺曼·福斯特(Norman Foster)事务所设计的伦敦瑞士再保险公司总部大楼(2004)是较早基于环境性能的协同找形案例(图10)。考虑到超高层建筑对周围气流的引导特征,整个设计利用空气动力学相关算法,以风压小、室内便于通风的限制条件作为制约因素,对建筑空间进行计算机模拟和风洞试验,从而生成得到螺旋曲面的建筑外形。此外,建筑内庭空间以螺旋状方式排布,同样是通风和采光共同需求的结果。

图7:基于生物几何系统的建筑转化

图8:利用不同树木分支结构组成的建筑拱形桁架

图9:基于结构性能的几何协同模拟(左为过程中的不同状态,右为最终的稳定形式)
无论是基于结构性能或是环境性能,这种几何协同的核心是建立起性能参数与几何形式的关联,并将动态的模拟过程明确地呈现在建筑师面前。作为结果,建筑形体不仅反映物质性能的需求,同时与生成逻辑相互匹配,从而为建筑创新提供具有信服力的设计依据。
4.几何重构
当下,复杂建筑形体涉及的材料尺寸、嵌板类型、曲面加工等建造问题,已成为几何学的重要议题。2007年,奥地利几何学家赫尔穆特·波特曼(Helmut Pottman)首次提出基于数字技术的“建筑几何学”(Architectural Geometry)[15]这一研究领域,2014年,他明确强调这一领域是面向复杂建筑形体建造的几何学设计,[16]其核心策略是几何重构。这是指利用可建造的单元拟合原始的复杂几何形态,重构出便于实质建造的近似形体,从而符合材料加工和施工成本的要求,包括曲面平板化、可展曲面[17]重构等操作方法。
弗兰克·盖里往往把可展曲面作为构成单元进行曲面重构,以便于真实建造。在设计之初,他一般使用草图和模型表达建筑形态,然后通过三维扫描将模型形态从实物传递到计算机,最后凭借计算机软件的几何解析能力进行优化与重构。在路易威登基金会艺术中心(2014)(图11),整个建筑通过优化成可展曲面的几何操作,表面的数千块玻璃板和近万块水泥板都采用单曲率面板,从而降低建造成本和施工难度。

图10:基于环境性能的伦敦瑞士再保险公司总部大楼螺旋曲面形式

图11:通过可展开面重构的路易威登基金会艺术中心
英国智能几何协会(Smartgeometry)在2012年木条网格壳体的编织过程中(图12),关注于测地线(Geodesic)的几何特征应用,设计者通过对自由曲面的曲率分析,生成并选择测地线来重构曲面。由于测地线是曲面空间中两点的局域最短路径,具有最小弯曲半径的特点,因此,建造过程中可方便使用直木条进行编织,不仅用料使用最省,而且可获得尽可能大的空间。
随着数字建构理论的出现和数控建造技术的发展,复杂建筑形体逐渐具有高性能的可建造性,并深刻地改变着从形式到建造的传统逻辑。在这一变化中,几何重构促使建筑设计过程和建造过程紧密相连,从起决定性的设计过程开始,通过几何操作获取与物质属性的内在关联,以实现形式、建造、经济三者的平衡。
四、传统的回归
基于以上分析,可以发现,数字时代的几何学正脱离几何的单纯美学架构,直接面对空间、环境和材料等建筑本体议题,建构一种以几何学为建筑策略的思维方法[18],从而使通过具体方法进行操作的几何逻辑,成为建筑自身的构建系统。这对于切石术、比例系统以及透视学中承载的几何操作而言,具有某种内在的一致性。
罗宾·埃文斯(Robin Evans)曾将建筑学中的几何学划分为三种类型:古典时代的“构成几何”、早期现代的“投射几何”和20世纪早期的“意指性几何”。[19]其中,他认为构成几何呈现为建筑物自身,两者融于一体,投射几何则是建筑学的制图工具,对于当时意指性的新几何学而言,罗宾斯有预见地提出批判性思考,认为其往往成为建筑的“符号”及“护身符”。[20]但正如他敏锐地指出,当时新几何学的建筑潜力尚未得到完全挖掘。[21]如今, 几何学正重塑在建筑学中的地位,不再是单纯的技术工具,而是面向建筑本体需求的设计思维。基于数字技术,建筑的形式系统已被发展整合为设计模型的几何呈现,背后的几何逻辑贯穿于从设计到建造的每一个环节,并在建筑外在表达上是一致的和可读的。因而,在这过程当中,以严谨的、科学的几何方式创新和实现复杂建筑形式成为某种必然。尽管这种方式下建筑呈现更多的是复杂的、动态的,但本质上是让几何学回归建筑学的传统(图13),基于建筑规则和逻辑,建筑师通过几何操作来控制设计与建造的多重维度需求。

图12:整个建造理念基于测地线几何特征的木条网格壳体

图13:几何学与建筑学关系演变的脉络归纳
结语
数字时代的几何学和建筑学是相互依赖和积极互动的,一方面,复杂建筑形体的生成和建造需要几何学理论作为支撑;另一方面,在整合功能、材料和建造的过程中,建筑所需的几何策略同样促进几何学的发展。然而,当数字设计作为一种通用知识和技术,易倾向于越加惊奇的复杂几何形式创作,以至于过分强调造型,这时需关注几何学在建筑学中适用性的问题。此外,无论是何种几何建构策略,都存在着局限性,比如几何生形往往使设计自由受到约束,几何重构容易导致最终形式偏离原先设计意图,等等。因此,如何以合理、高效的几何途径实现全新的建筑形式,并把控从设计到建造的全过程,仍需持续而深入的探索。
注释
[1]Branko Kolarevic.Architecture in the digital age:design and manufacturing[M].Taylor &Francis,2005:25.
[2]Toni Kotnik.There is geometry in architecture[C]//Selforganizing Forms and Pprocesses:Symposium 2014.IUP,2014(1):36.
[3]Achim Menges.The new cyber-physical making in architecture:computational construction[J].Architectural Design,2015,85(5):32.
[4] 大卫 · M.雅各布森 · 解密哈德良时期的建筑及其几何学[C]//建筑文化研究[7].同济大学出版社,2015:21.
[5]Antoine Picon.Architecture and mathematics:Between hubris and restraint[J].Architectural Design,2011,81(4):31.
[6]Mario Carpo.Drawing with numbers:geometry and numeracy in early modern architectural design[J].Journal of the Society of Architectural Historians,2003,62(4):449.
[7]Robin Evans.The projective cast: architecture and its three geometries[M].MIT press,2000:151.
[8]同6:456.
[9]同7:326-327.
[10]Mark Burry.Geometry Working Beyond Effect[J].Architectural Design, 2011,81(4):81.
[11]同7:xxvii.原文为Whan I mean by a dead geometry is an aspect of geometry no longer under development from within.Dead geometry is an innoculation against uncertainty.
[12]同10:83.
[13]Iannis Xenakis.Music and architecture:architectural projects,texts,and realizations[M].Pendragon Press,2008:98.
[14]Mario Carpo.The digital turn in architecture 1992-2012[M].Wiley,2012:12.
[15]Helmut Pottmann,Andreas Asperl,Michael Hofer,et al.Architectural Geometry[M].Bentley Institute Press,2007:145-164.
[16]Helmut Pottmann,Michael Eigensatz,Amir Vaxman,et al.Architectural Geometry[J].Computers&Graphics,2015(6):145-164.
[17]可展曲面:属于直纹面,可以保长变换到平面中完全贴合,便于加工,一直被广泛应用于工业制造领域,弗兰克 · 盖里是第一个将可展曲面引入建筑工程的建筑师。
[18]Jane Burry,Mark Burry.The new mathematics of architecture[M].Thames & Hudson,2010:13.
[19]同7:349.原文为compositional geometry、projective geometry、signified geometry.
[20]同7:349.原文为The same mentality affected the appropriation of new geometry,which became an inspirational talisman of considerable power.
[21]同7:349.
图片来源
图1:Robin Evans.The projective cast: architecture and its three geometries[M].MIT press,2000:185.
图2:同上:326.
图3:https://www.archdaily.com/797419
https://www.archdaily.com/591415/spotlight-felix-candela
https://www.archdaily.com/644580/spotlightpier-luigi-nervi-2/
https://www.archdaily.mx/mx/02-98249
https://www.pritzkerprize.com/laureates/frei-otto
https://en.wikipedia.org/wiki/Buckminster_Fuller
https://structurae.net/structures/deitingen-service-station
图4:http://glform.com/buildings/h2-house/
http://www.architectmagazine.com/projectgallery/walt-disney-concert-hall_o
http://www.zaha-hadid.com/architecture/bergisel-ski-jump/
图5:http://www.archdaily.com/796428/toyoitos-taichung-metropolitan-opera-housephotographed-by-lucas-k-doolan.
图6:http://www.archdaily.com/33238/nationallibrary-in-astana-kazakhstan-big/.
图7-1:Simon Bechert,Jan Knippers,Oliver David Krieg,et al.Textile Fabrication Techniques for Timber Shells[C]//AAG 2016.vdf Hochschulverlag,2016:158/164.
图7-2:http://icd.uni-stuttgart.de/?p=16220.
图8:http://designandmake.aaschool.ac.uk/woodchip-barn/.
图9:http://icd.uni-stuttgart.de/?p=6553.
图10:http://www.fosterandpartners.com/projects/30-st-mary-axe/.
图11:http://www.fondationlouisvuitton.fr/en/l-edifice.html.
图12:http://matsysdesign.com/2012/04/13/sg2012-gridshell/.

