渗透系数级差对污染物在低渗透透镜体中的迁移影响研究

赵勇胜,韩慧慧,迟子芳*,李 琴,康学赫,刘茹雪



渗透系数级差对污染物在低渗透透镜体中的迁移影响研究

赵勇胜1,2,韩慧慧1,2,迟子芳1,2*,李 琴1,2,康学赫1,2,刘茹雪1,2

(1.吉林大学,地下水资源与环境教育部重点实验室,吉林 长春 130021；2.吉林大学新能源与环境学院,吉林 长春 130021)

利用二维模拟槽研究非均质含水层中渗透系数级差对低渗透透镜体内污染物迁移的影响,确定不同渗透系数级差下污染物在透镜体中的波及效率和去除效率,建立低渗透透镜体内波及/去除效率、入渗/反冲时间和渗透系数级差三者之间的定量关系.结果表明:在污染过程中,污染物的迁移速度随渗透系数级差的增大而减小;在0.5m/d的地下水流速下,当渗透系数级差从3增大至52时,污染物波及效率达到100%所需要的时间从8h上升至360h;污染物的波及效率与入渗时间成正相关关系与渗透系数级差mn呈负相关关系,其函数关系为=(109.623/mn2+1.035/mn+0.447).在模拟抽出处理的过程中,污染物的去除速度随渗透系数级差的增大而减小;当渗透系数级差从3增大至52时,污染物的去除效率达到100%所需的时间从13h升高至480h;污染物在透镜体中的去除效率’与反冲时间和渗透系数级差mn的函数关系为’=(54.999/mn2+6.605/mn+0.098).对比两个过程可发现,污染物在非均质含水层中的污染和修复过程在时间方面呈现出不可逆性.随着渗透系数级差的增大,污染和去除过程中低渗透透镜体内波及/去除效率达100%的时间差值从5h逐渐增大至120h,“拖尾”效应越来越明显.

渗透系数级差；低渗透透镜体；波及效率；去除效率

近年来,地下水污染问题日益严重[1-4],污染场地的修复和治理得到了高度重视,为了制定经济有效的修复方案,必须掌握污染物在地下迁移的规律,预测污染范围及其迁移路径.非均质含水层中污染物的迁移情况更为复杂[5-6],特别是在地下广泛存在的低渗透透镜体的修复过程中,修复试剂在高渗透区易形成“优先流”在低渗透区易形成“绕流”现象,导致其在低渗透介质中的迁移效率低;并且当高渗透区的污染物浓度降低后,低渗透区的污染物在浓度梯度的作用下会持续不断的向高渗透区扩散释放,导致污染物的“拖尾”效应.因此,确定非均质含水层中渗透系数级差对污染物的滞留及迁移影响对非均质含水层的污染修复具有重要意义.

室内二维模拟槽目前已成为研究多相流迁移、污染物迁移及修复[7-8]等问题的重要工具.图像分析法是模拟槽实验中考察溶质运移过程的一种常用方法[9-11],该方法具有直观性、图像易采集性、费用低等优点.亮蓝因背景值低、毒性低、溶解度高,与含水层介质颜色形成鲜明对比,具有良好的移动性和可视性,因此被大量研究采用[12-16].目前已有大量学者对非均质含水层中污染物的迁移规律进行研究[17-20].Brendan等[21]以1.32mL/min的流速注水反冲洗预先饱和染料的二维模拟槽,研究非均质中低渗透区的溶质运移问题,研究发现,当渗透系数级差为6时染料主要发生宏观弥散不产生拖尾效应,渗透系数级差为300时染料运移以对流为主并产生拖尾效应,渗透系数级差达到1800时染料主要发生分子扩散,并且拖尾现象最为明显.陈震等[22]研究发现在渗透系数级差为80和150的非均质条件下亮蓝在模拟槽内的最大贮存质量与渗透系数级差呈负相关关系,与注入速度呈正相关关系.程洲等[23]在表面活性剂原位冲洗修复试验中发现透镜体内TCE的修复效率随渗透系数级差的增大而减小.Yang等[24-26]发现在粗砂/粘土高渗透系数级差下染料会在低渗透区发生缓慢的反向扩散,形成二次污染源.现有研究主要是针对渗透系数级差与污染物运移规律的定性研究,并没有给出污染物的迁移规律与渗透系数级差和时间的定量关系.因此本实验在前人研究的基础上,以亮蓝代替可混溶的非反应性污染物,通过室内二维模拟槽实验研究不同渗透系数级差条件下低渗透透镜体中污染物的迁移规律,建立污染物的波及效率和去除效率与渗透系数级差和入渗/反冲时间的定量关系,以期为非均质污染含水层中低渗透地层污染范围和抽出处理时间的确定提供理论依据.

1 材料与方法

1.1 实验装置

实验装置选用尺寸为500×400×50mm的二维有机玻璃槽,两侧设有20mm布水隔室,如图1所示.实验采用湿法填砂[27],避免干法填砂后期饱水时产生气泡而改变介质的渗透性.在模拟槽正中间装填一个长25cm、宽5cm、高10cm的低渗透透镜体.装填过程中,保持砂箱中水位高于石英砂1~2cm,每装填2cm石英砂后用铝锤夯实,保证介质完全饱水且填充均匀.装填外围介质时,控制相同质量石英砂装填高度相同,使每组实验中相同外围介质的渗透系数不变.

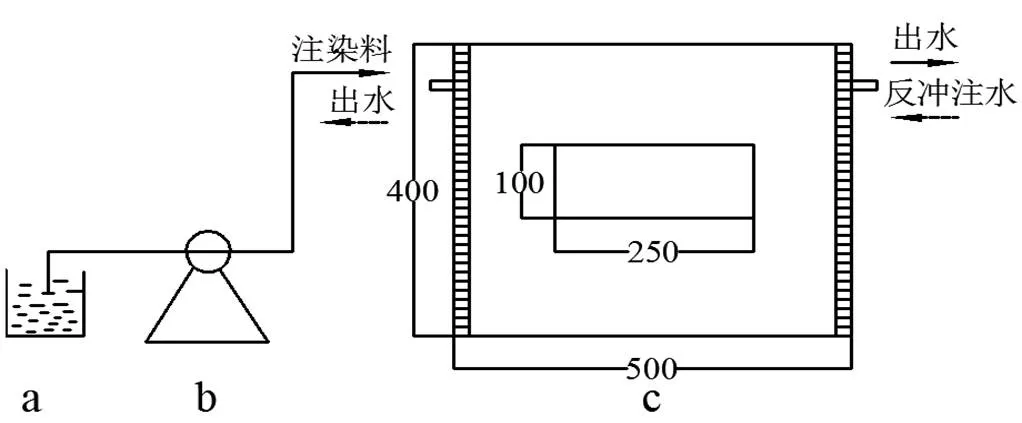
图1 实验装置示意

a.染料b.蠕动泵c.模拟槽

1.2 实验材料

实验采用可食用的亮蓝染料代替可混溶的非反应性污染物;为了便于观察污染物的迁移过程,采用含泥量低、染色效果明显的白色石英砂模拟含水层介质(购自新沂市明亮石英砂厂).6种介质岩性及其物理特性如表1所示.

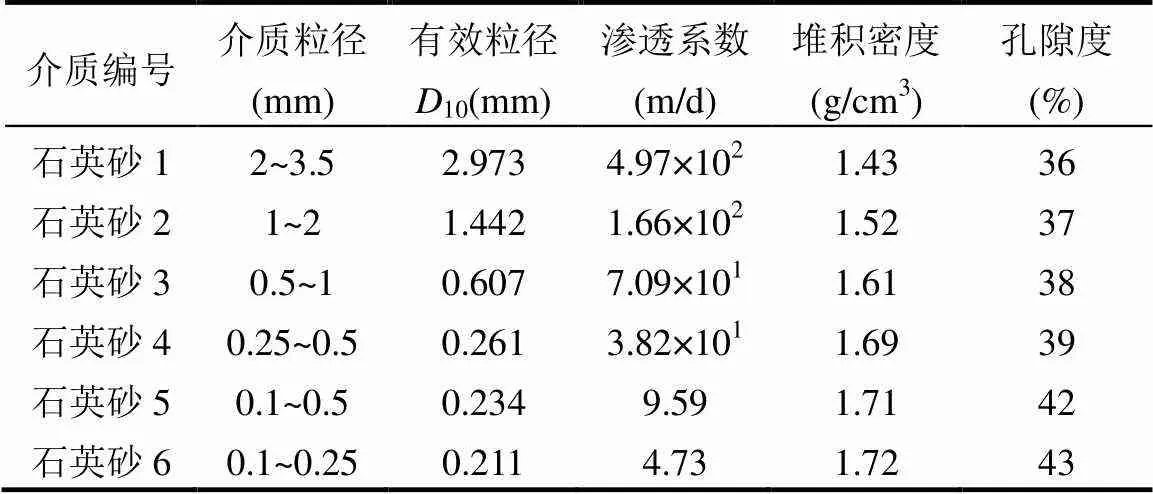
表1 模拟含水层介质物理特性

1.3 实验方法

二维模拟槽高渗透区装填介质粒径为2~ 3.5mm,低渗透透镜体分别选用5种介质,粒径分别为1~2mm、0.5~1mm、0.25~0.5mm、0.1~0.5mm、0.1~0.25mm.设置地下水流速为0.5m/d,利用蠕动泵以6.5mL/min的速度注入100mg/L的亮蓝溶液,以染料刚接触透镜体边缘为起始点,染料完全穿透透镜体为终点计时,在相同时间间隔下在二维模拟槽上对透镜体中染色的区域锋面画线记录,以用来分析透镜体的整个污染过程,同时拍摄照片,利用GMS软件对图片进行后期处理,计算每个时间段染料进入透镜体中的面积,研究不同渗透系数级差下低渗透透镜体中污染物的迁移规律.每组实验监测的时间间隔根据染料在透镜体中的迁移速度设置,具体设计如表2所示.待整个二维模拟槽完全染色后,以相同的流速注清水反向冲洗(模拟抽出处理技术),以注入水刚接触染色透镜体边缘为起始点,透镜体中染料被完全冲出为终点计时,采用上述方法画线记录染料的迁出过程并拍摄照片,利用GMS软件求出每个时间段染料从透镜体中的迁出面积,研究不同渗透系数级差下低渗透透镜体中污染物的去除规律.

表2 实验方案一览表

2 结果与讨论

2.1 渗透系数级差对非均质含水层污染过程的影响

不同渗透系数级差下不同时刻污染物进入透镜体的迁移情况如图2所示,图中黑色矩形内为低渗透透镜体区域,矩形外围为高渗透区域,黑色标记线为相同时间间隔下污染物的迁移范围.

图2 不同渗透系数级差下染料进入透镜体的迁移过程

虽然污染物的注入方式和速度相同,但受介质的非均质性影响,污染物在低渗透透镜体中的迁移行为表现出显著差异.如图所示,当渗透系数级差为3时,污染物完全穿透透镜体需要8h,渗透系数级差为7时需要40h,渗透系数级差为13时需要90h,渗透系数级差为52时所需时间上升至360h,而此时渗透系数级差为105的透镜体中污染物的波及效率仅达到87.14%.渗透系数级差越大,污染物进入低渗透区越慢,在低渗透区的迁移速度越小.当mn=52和105时,透镜体中污染物的浓度低于高渗透区的浓度,渗透系数级差越大,进入透镜体中染料的颜色越浅,浓度越低.污染物在低渗透区既有横向迁移又有纵向迁移,并且纵向迁移在开始注入污染物一段时间后才开始显现,这是因为横向迁移时主要受水动力作用,而纵向迁移主要受分子扩散作用的影响.由于扩散作用力小于水动力作用力,所以纵向迁移速度低于横向迁移速度.

利用GMS软件分析一定时间内污染物在低渗透透镜体中的迁移面积,并计算其占低渗透区域总面积的比例,将其定义为波及效率,计算公式如(1)所示.

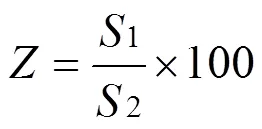
式中:为波及效率;1为透镜体中被染料染色区域的面积,cm2;2为透镜体的总面积,cm2;不同渗透系数级差的非均质介质中,污染物在透镜体中的波及效率随时间变化如图3所示.

图3 不同渗透系数级差下污染物在透镜体中的波及效率

Fig.3 The sweep efficiency of dyes in the lens under different permeability ratio

当渗透系数级差从3逐渐升高到52时,污染物波及效率达到100%所需要的时间从8h大幅度上升到360h.这是因为介质粒径越小,渗透系数越小,透水性越弱,当污染物运移到透镜体界面时,需要克服的阻力变大,形成阻挡屏障,因此发生绕流现象.渗透系数级差越大的透镜体阻力越大,绕流现象越明显.由图3还可见,当渗透系数级差为3、7、13时,波及效率与时间呈线性相关关系,当渗透系数级差为52、105时,明显不是线性关系,为了获得波及效率的变化速率,对曲线前半段(£192h)进行线性拟合,其拟合方程及相关系数如表3所示.随着时间延长,波及效率直线的斜率略有减小,且渗透系数级差越大,曲线斜率变化趋势越缓,说明污染物在透镜体中的迁移速度变小.这是因为污染物在透镜体中迁移时,对流作用随着迁移距离增大而减小,污染物迁移的有效动力变小.

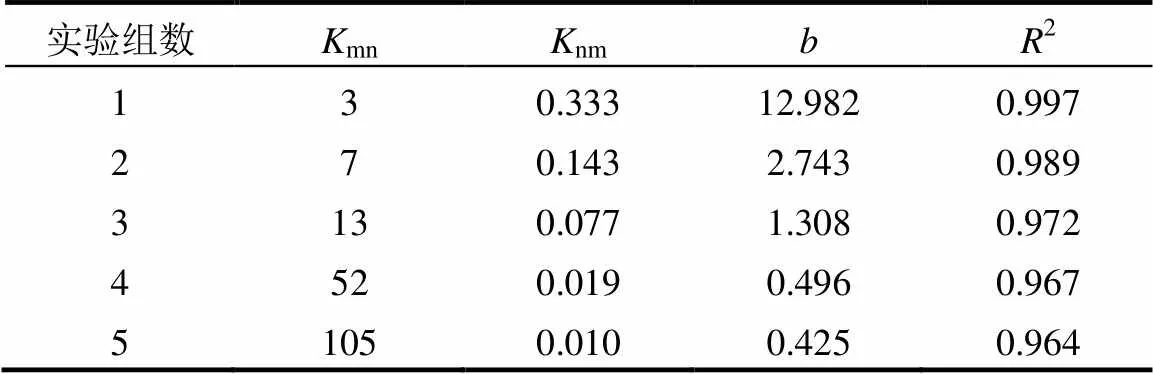
表3 污染物的波及效率Z与时间t关于Z=bt线性拟合方程

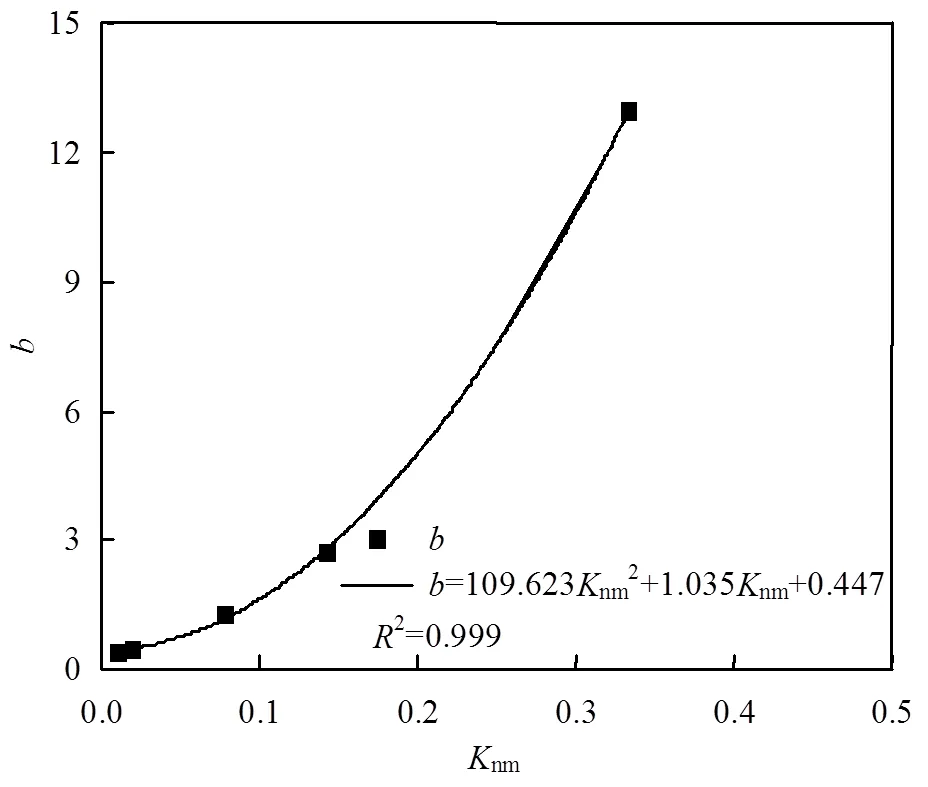
图4 b关于Knm的二次多项式方程拟合

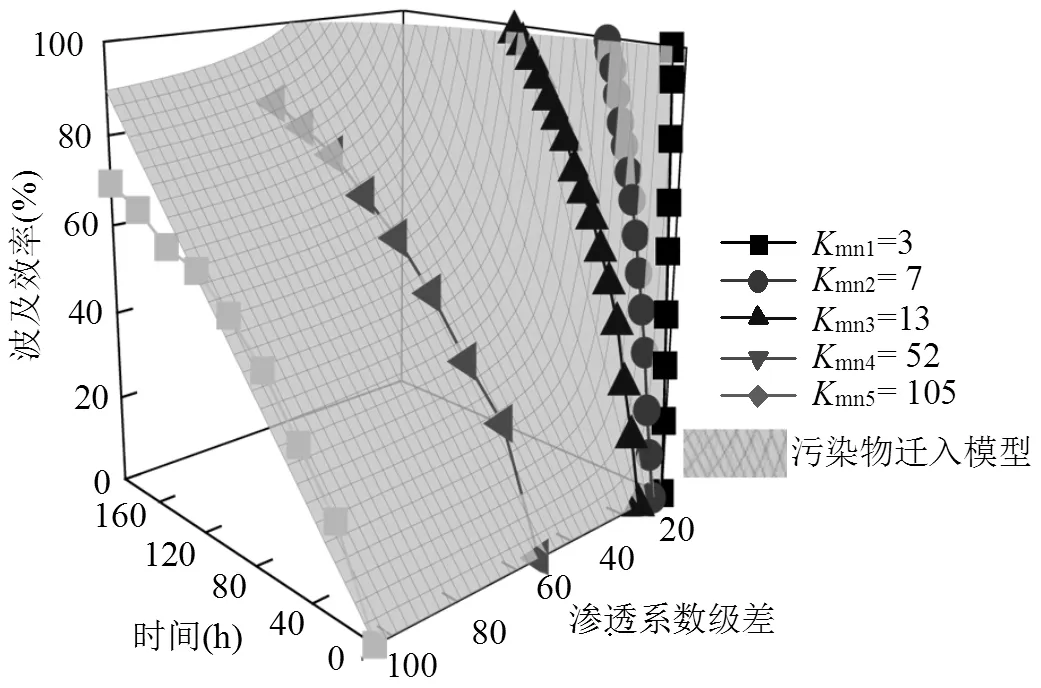
图5 污染物在透镜体中迁移的三维模型

不同渗透系数级差非均质含水层中污染物波及效率直线方程的斜率相差较大,考察其与mn的关系,发现与mn的倒数nm正相关,建立与nm的函数关系,如图4所示.将与mn函数关系带入污染物波及效率方程,得到污染物波及效率与渗透系数级差mn及入渗时间的函数关系:=(109.623/mn2+1.035/mn+0.447),三维模型表达如图5所示.将原始数据带入进行模型拟合,发现实验数据与模型具有较好的拟合效果,说明此模型可以模拟污染物在非均质含水层中的迁移情况.

2.2 渗透系数级差对非均质含水层中污染物迁移的影响

待二维模拟槽完全染色,以相同的流速注清水反向冲洗模拟抽出处理技术,不同渗透系数级差下不同时刻透镜体中污染物的去除情况如图6所示,黑色标记线为相同时间间隔下污染物的去除范围.

图6 不同渗透系数级差下污染物在透镜体中的去除路径

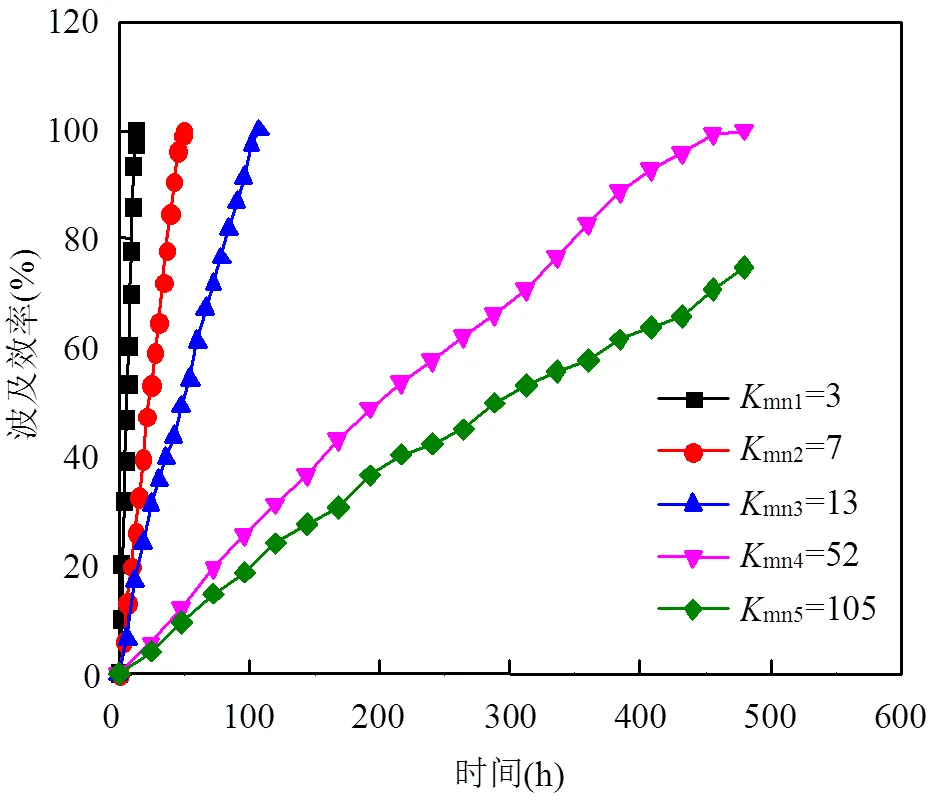
图7 污染物在不同渗透级差透镜体中的去除效率

从图6可以看出,污染物的去除路径最后都形成了羽状,发生了拖尾效应.当渗透系数级差为3、7时拖尾现象不够明显,当级差增大至13、52、105时,拖尾现象越来越明显.当渗透系数级差为3时,污染物全部去除需要13h,渗透系数级差为7时需要49h,渗透级差为13时需要108h,渗透系数级差为52时大幅度上升至480h,而此时渗透系数级差为105的透镜体中污染物的去除效率仅达到74.67%.渗透系数级差越大,污染物越难从透镜体中去除.

利用GMS软件计算一定时间内污染物从透镜体中的迁出面积,不同渗透系数级差的非均质介质中,污染物在透镜体中的去除效率随时间变化如图7所示.

由图7可知,渗透系数级差越大,染料被完全冲出透镜体所需要的时间越长,速度越慢.这是因为染料主要靠水动力被去除,渗透系数级差越大,低渗透区渗透系数越小,水进入透镜体需要克服的阻力越大,透镜体中染料获得的有效动力越小,越难被去除,拖尾现象越明显.污染物的去除效率与时间呈线性相关关系,其拟合方程及相关系数如表4所示

同理,考察与mn的关系,建立与nm的函数关系,如图8所示.将与mn函数关系带入污染物去除效率方程,得到污染物去除效率’与渗透系数级差mn及反冲时间的函数关系:’=(54.999/mn2+ 6.605/mn+0.098),三维模型表达如图9所示.将原始数据带入进行模型拟合,发现实验数据与模型具有较好的拟合效果,说明此模型可以模拟抽出处理过程中非均质含水层中污染物的去除情况.依据此模型,为抽出处理的时间确定提供理论依据.

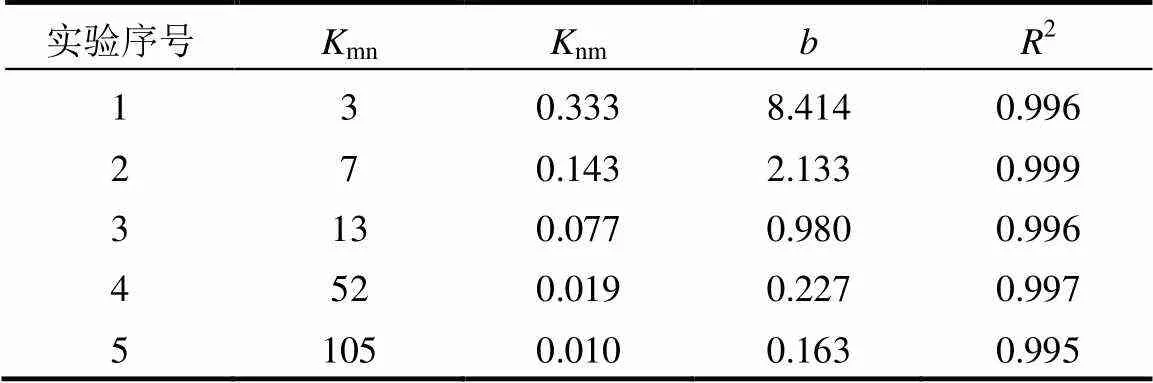
表4 污染物的去除效率Z’与时间t关于Z’=bt线性拟合方程

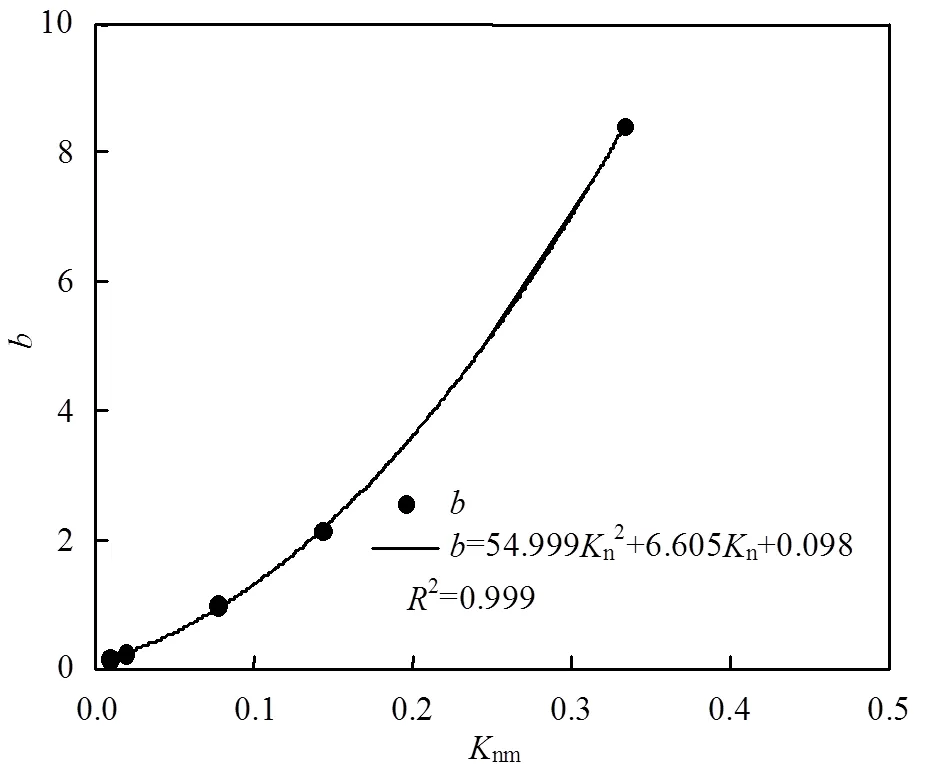
图8 b关于Knm的二次多项式方程拟合

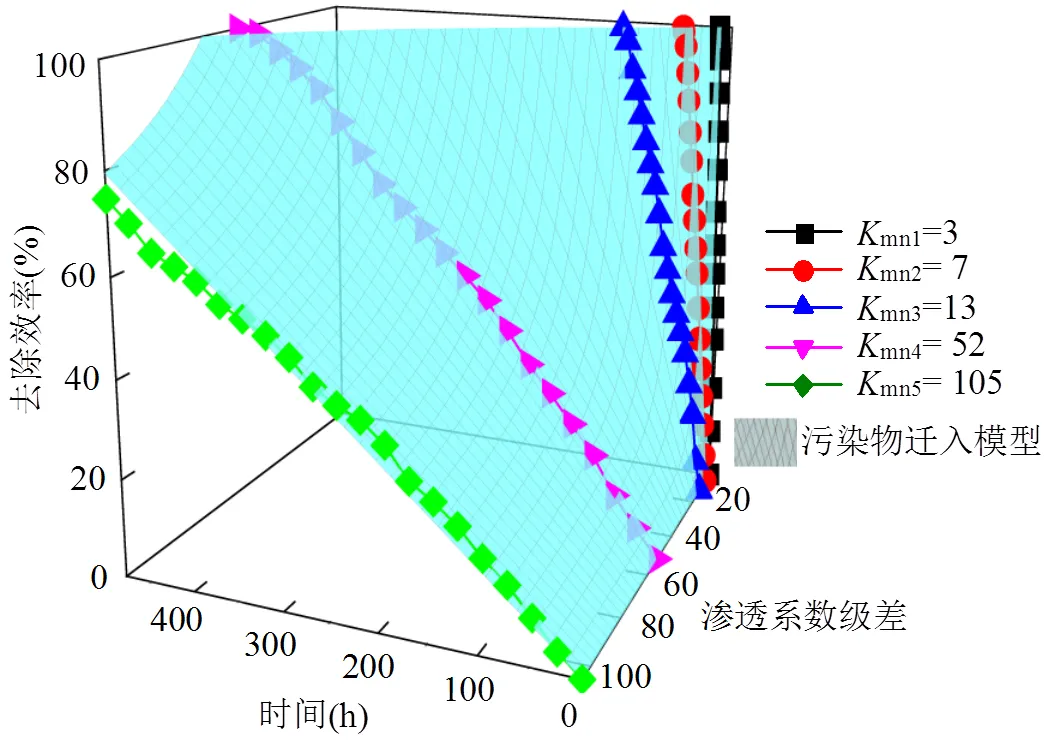
图9 污染物从透镜体中去除的三维模型

2.3 渗透系数级差对非均质含水层中污染物滞留的影响

将上述污染物在非均质含水层中的迁入和迁出方程建立三维模型,如图10所示.

从图中可以看出,相同条件下,污染物在同一透镜体的波及效率都大于其去除效率,即污染物进入透镜体的速度大于被冲出的速度.这是因为污染物进出透镜体过程中受到的水动力是相同的,但是进入透镜体时,不断注入的污染物相当于一个泄露的污染源,高渗透区污染物的浓度始终高于透镜体中的浓度,这种较大的浓度梯度导致染料分子扩散的速度很快;而在反冲洗时,由于非均质的影响,高渗透区的污染物最先被去除,这时透镜体中的污染物相当于污染源,在不断的反冲下,透镜体内污染物浓度越来越低,与高渗透区中污染物的浓度梯度越来越小,所以染料分子扩散速度变小,而且介质对污染物具有一定的吸附作用,所以污染物的迁入速度大于其迁出速度,这种在透镜体中的易进难出表现为拖尾效应.当渗透系数级差为3时,污染物完全进入透镜体的时间与被去除的时间相差5h,渗透系数级差为7时相差9h,渗透系数级差为13时相差18h,渗透系数级差为52时相差120h,拖尾效应随着渗透系数级差的增大表现的更加明显,这是因为渗透系数级差越大的非均质中低渗透区的渗透系数越小,对污染物的阻截能力越强,污染物扩散出去的速度越慢.

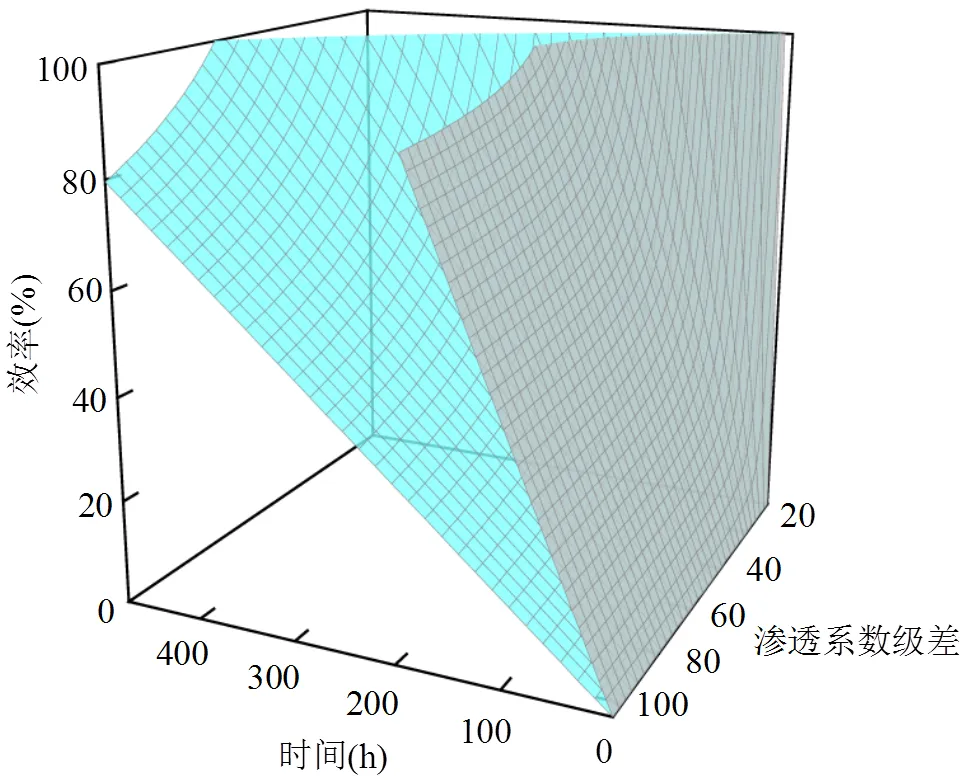
图10 污染物波及效率与去除效率的关系

3 结论

3.1 非均质含水层的渗透系数级差越大,污染物进入低渗透透镜体中所需的时间越长;污染物在透镜体中的波及效率与渗透系数级差mn及时间的关系:=(109.623/mn2+1.035/mn+0.447),依据此方程,可以预测污染源泄露之后,污染物在低渗透介质中的波及情况.

3.2 非均质含水层的渗透系数级差越大,污染物在透镜体中的滞留时间越长;污染物从透镜体中的去除效率’与渗透系数级差mn及时间的关系:’=(54.999/mn2+6.605/mn+0.098),依据此模型,为污染地下水抽取处理的时间确定提供理论依据.

3.3 非均质含水层中,污染物在透镜体中的波及效率大于其去除效率;从透镜体中去除的时间大于其进入的时间,并且随着渗透系数级差的增大,污染物去除和进入的时间差值从5h逐渐增大至120h,拖尾现象越明显,需要修复时间越长.

[1] Michael Berg, Con Tran H, T C N, et al. Arsenic Contamination of Groundwater and Drinking Water in Vietnam:  A Human Health Threat [J]. Environmental Science & Technology, 2001,35(13):2621- 2626.

[2] Qiu J. China faces up to groundwater crisis [J]. Nature, 2010, 466(7304):308.

[3] Gong J, Tang K, Wang H. Zone-division of water crisis and corresponding strategies in China [J]. Resources Science, 2015.

[4] Lin K S, Mdlovu N V, Chen C Y, et al. Degradation of TCE, PCE, and 1,2–DCE DNAPLs in contaminated groundwater using polyethylenimine-modified zero-valent iron nanoparticles [J]. Journal of Cleaner Production, 2018,175:456-466.

[5] Yang M, Annable M D, Jawitz J W. Forward and back diffusion through argillaceous formations [J]. Water Resources Research, 2017, 53:4514-4523.

[6] Tatti F, Papini M P, Sappa G, et al. Contaminant back-diffusion from low-permeability layers as affected by groundwater velocity: A laboratory investigation by box model and image analysis. [J]. Science of the Total Environment, 2018,s622–623:164-171.

[7] Fure A D, Jawitz J W, Annable M D. DNAPL source depletion: linking architecture and flux response. [J]. Journal of Contaminant Hydrology, 2006,85(3):118-140.

[8] Clement T P, Kim Y C, Gautam T R, et al. Experimental and Numerical Investigation of DNAPL Dissolution Processes in a Laboratory Aquifer Model [J]. Groundwater Monitoring & Remediation, 2004,24(4):88-96.

[9] Kashuk S, Mercurio S R, Iskander M. Visualization of dyed NAPL concentration in transparent porous media using color space components [J]. Journal of Contaminant Hydrology, 2014,162-163(5): 1-16.

[10] Corapcioglu Y M, Chowdhury S, Roosevelt S E. Micromodel visualization and quantification of solute transport in porous media [J]. Water Resources Research, 1997,33(11):2547-2558.

[11] Konz M, Ackerer P, Huggenberger P, et al. Comparison of light transmission and reflection techniques to determine concentrations in flow tank experiments [J]. Experiments in Fluids, 2009,47(1):85-93.

[12] Flury M, Flühler H. Brilliant Blue FCF as a Dye Tracer for Solute Transport Studies—A Toxicological Overview [J]. Journal of Environmental Quality, 1994,23(5):1108-1112.

[13] Smart P L, Laidlaw I M S. An Evaluation of Some Fluorescent Dyes for Water Tracing [J]. Water Resources Research, 1977,13(13):15-33.

[14] Wang K, Zhang R. Heterogeneous soil water flow and macropores described with combined tracers of dye and iodine [J]. Journal of Hydrology, 2011,397(1/2):105-117.

[15] 王泽坤.含有透镜体的二维多孔介质溶质运移实验与模拟研究[D]. 合肥:合肥工业大学, 2017.

[16] 刘登峰.黄原胶强化传输多硫化钙修复铬(Ⅵ)污染非均质含水层研究[D]. 长春:吉林大学,2016.

[17] Chapman S W, Parker B L. Plume persistence due to aquitard back diffusion following dense nonaqueous phase liquid source removal or isolation [J]. Water Resources Research, 2005,41(12):2179-2187.

[18] Travis C, Doty C. ES & T Views: Can contaminated aquifers at superfund sites be remediated [J]. Environmental Science & Technology, 1990,24(10):1464-1466.

[19] Frank U, Barkley N. Remediation of low permeability subsurface formations by fracturing enhancement of soil vapor extraction [J]. Journal of Hazardous Materials, 1995,40(2):191-201.

[20] Berglund S, Cvetkovic V. Pump-and-Treat Remediation of Heterogeneous Aquifers: Effects of Rate-Limited Mass Transfer [J]. Ground Water, 2010,33(4):675-685.

[21] Brendan Zinn, L C M, C F H , et al. Experimental Visualization of Solute Transport and Mass Transfer Processes in Two-Dimensional Conductivity Fields with Connected Regions of High Conductivity [J]. Environmental Science & Technology, 2004,38(14):3916-3926.

[22] 陈 震.层状非均质含水层污染与水动力修复过程中污染物的迁移规律研究 [D]. 长春:吉林大学, 2018.

[23] 程 洲,吴吉春,徐红霞,等.DNAPL在透镜体及表面活性剂作用下的运移研究[J]. 中国环境科学, 2014,34(11):2888-2896.

[24] Yang M, Annable M D, Jawitz J W. Back Diffusion from Thin Low Permeability Zones [J]. Environmental Science & Technology, 2015, 49(1):415-22.

[25] Yang M, Annable M D, Jawitz J W. Field-scale forward and back diffusion through low-permeability zones. [J]. Journal of Contaminant Hydrology, 2017,202:47-58.

[26] Yang M, Annable M D, Jawitz J W. Solute source depletion control of forward and back diffusion through low-permeability zones. [J]. Journal of Contaminant Hydrology, 2016,193:54-62.

[27] Heidari P, Li L. Solute transport in low-heterogeneity sandboxes: The role of correlation length and permeability variance [J]. Water Resources Research, 2015,50(10):8240-8264.

Study on the influence of contrasts of hydraulic conductivity on the migration of contaminants in low-permeability lens.

ZHAO Yong-sheng1,2, HAN Hui-hui1,2, CHI Zi-fang1,2*, LI Qin1,2, KANG Xue-he1,2, LIU Ru-xue1,2

(1.Key Laboratory of Groundwater Resources and Environment, Ministry of Education Jilin University, Changchun 130021, China；2.College of New Energy and Environment, Jilin University, Changchun 130021, China)., 2018,38(12)：4559~4565

Two-dimensional chambers were used to study the influence of permeability on the pollutant migration in the low-permeability lens of heterogeneous aquifer, and the spreading and removal efficiency of contaminant was calcuated. Also, a quantitative relationship between the spreading/removal efficiency, the contrasts of hydraulic conductivity and the time was established as a consquence. Results showed that the dye’s migration speed got slower as the contrast of hydraulic conductivity increased, and the time of getting 100% dye’s spreading efficiency increased from 8 to 360 hours when the contrasts of hydraulic conductivity increased from 3 to 52 at a natural groundwater flow rate of 0.5m/d. The spread efficiency of the pollutant is positively correlated with the time but negatively correlated with the contrasts of hydraulic conductivity, and the function could be expressed as:=(109.623/mn2+1.035/mn+0.447). Then water was injected to flush the dye at the same flow rate of 0.5m/d to simulate the Pump-and-Treat Technique to remediate the contaminant. Results showed that the larger of the contrast of hydraulic conductivity, the faster of the removal rate. When the contrast of hydraulic conductivity increased from 3 to 52, the removal time dye increased from 13 to 480 hours, and the fuction of the spreading/removal efficiency with cont-rasts of hydraulic conductivity and time could be expressed as:’=(54.999/mn2+6.605/mn+0.098). Comparing the two processes, it can be found that the pollution and remediation process of the contaminant in the heterogeneous aquifer is irreversible in terms of time.Under the same conditions, the entry rate of the dye was always lager than the removal rate, and the time difference increased gradually from 5 to 120 hours with the increase of the contrast of hydraulic conductivity, which means the tailing effect becoming more and more obvious.

contrasts of hydraulic conductivity；low-permeability lens；spread efficiency；removal efficiency

X523

A

1000-6923(2018)12-4559-07

赵勇胜(1961-),男,内蒙达茂旗人,吉林大学环境与资源学院环境工程系教授,博士,主要从事水土污染控制与修复方面的研究.发表论文52篇.

2018-04-23

国家自然科学基金重点项目(41530636);国家自然科学基金面上项目(41772244);国家留学基金资助项目(201806175055)

* 责任作者, 副教授, chizifang@jlu.edu.cn