变形监测数据处理方法研究

张祖敏，李琛阜

（核工业赣州工程勘察院，江西 赣州 341000）

所谓变形，即是指某物体在某种或多种外力作用下，其位置、形状在空间域和时间域中发生变化的现象。变形监测的目的是通过监测数据的获取，对监测数据进行分析，从而找到变形产生的原因，对变形的预测预报。下面主要对多元线性回归分析法、BP神经网络模型和灰色系统理论进行讨论。

1 多元线性回归分析法

多元回归分析是目前使用比较多的变形监测数据分析方法。它主要研究一对多，即一个变量与多个因变量之间的相关关系[1]。其数学模型为

上述模型用矩阵表示为

式中，y为n维变形观测了量且y=(y1，y2，……，yn)T。X为可控制的变量观测值或函数。

根据最小二乘原理来求得β的估值是

实际上，上式得到的估值只是就观测值初步分析得到的假设，故在得到多元回归方程后还必须对其进行统计检验，即检验此估值是不是无偏估计值，检验包括回归系数显著性检验和回归方程显著性检验。

取文献中实例，上海地区某建筑物其地基为软土，需要对其进行长期一段时间的沉降监测，监测数据采用多元线性回归模型进行分析，将前21期观测资料用来建立模型，后5期观测资料用来比较预测值与实际值的差异。

（1）初步建立回归方程为：

（2）建立变形点误差方程为：

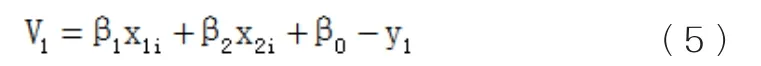
在matlab中计算其最小二乘解得：

故由以上可得变形点1的多元回归线性方程：

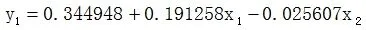
对变形点进行回归系数显著性检验和回归方程显著性检验可得均显著故可预测后5期沉降值为：

表1 变形点后5期真实沉降值与预测值

根据上表，由后5期预测值与真实值比较接近，表示该模型的预测结果是相对准确的。

2 BP神经网络

BP网络全称为反向传播（Back Propagation）神经网络，它是由非线性普通变换单元组成的前馈型网络，是当今最主流的神经网络模型之一。

（1）正向传播阶段：计算网络结构的实际输出值

令输入层输出值等于输入值，即Bi=xi

计算隐含层输入值为：

计算隐含层输出值为：

式中，f为Sigmoid函数；θk为隐含层节点k的阈值。

计算输出层输入值为：

计算输出层输出值为：

（2）反向传播阶段：计算误差函数

计算输出层节点j的误差为：

计算目标函数为：

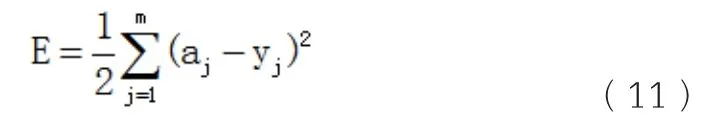
比较E与设定值的大小，判断是否需要调整权值大小重新计算。

（3）改变权值w的大小为：

将权wki调整为：

式中，u是训练速率，取u=0.01～1

接着完成所有训练样本直至均满足要求，此时BP网络算法已完成。

取文献中实例，上海地区某建筑物其地基为软土，需要对其进行长期一段时间的沉降监测，监测数据采用多维输入的BP神经网络模型对变形点1进行分析。

由于影响地基沉降的因子主要为时间和荷载（在多元线性回归分析中已证明），所以在此BP神经网络中取2个输入层神经元（分别为每期的时间序列和荷载），5个隐含层神经元，1个输出层神经元（即每期的沉降量序列）。输入层和输出层一共构成24个匹配对，用前面16个匹配对作为BP模型的训练样本，后面8个匹配对用于预测及检验其正确性。

分别为：

3 灰色系统理论

谓灰色系统理论，是在给予信息量不够的情况下，采用数据重生成的方法将混乱的原始数据整理成强规律性的数据序列。

在变形监测的预测中一般采用一阶一个变量的微分方程。即GM（1，1）模型，其建模过程如下：

（1）设原始非负数列为

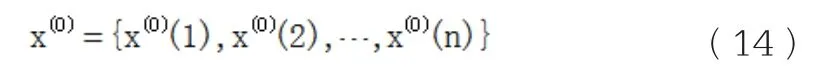
（2）对原始数列进行1-AGO得

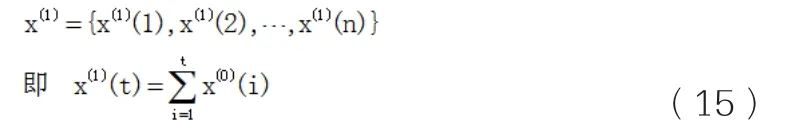
（3）还原数据，作IAGO得：

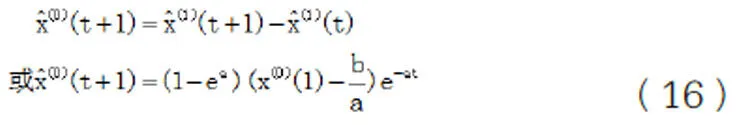
t＜n时，上式即为拟合模型；t=n时，上式即为滤波模型；t＞n时，上式即为预测模型。

以南京市中心医院全国中心楼基坑位移为例，对压顶圈梁上7号点的水平位移资料采用GM（1，1）模型进行分析，用模型对前7期进行模拟，对后7期进行预测，比较成果。

观测数据序列为

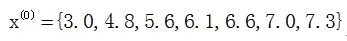
作1-AGO得：

由最小二乘法：

计算模型表达式为

4 三种分析方法的对比

（1）在变形监测数据预处理方面的差异。不同的数据分析方法对原始数据的要求也不尽相同，我们在使用某种分析方法或建模之前，需要对原始数据进行符合分析方法要求的处理。①在多元线性回归分析中，其整个分析过程是建立在原始数据满足线性关系的，所以我们需要提前将原始数据进行预处理，即画出图形来观察判断原始数据的线性相关性，如果不满足线性相关，则必须预处理再进行回归分析。②在神经网络分析中，我们要预处理原始数据进行中心化转换，来符合输入数据序列的要求。

（2）各自的优缺点。①多元线性回归分析可以比较准确得判断各个因子之间的相关性以及拟合程度的高低。②人工神经网络具有大量优点，比如它具有很高的容错性；由于它的并行性使它处理信息的速度非常快；即使系统复杂多变，它也能自己学习、自己适应并且稳定预测。③灰色系统理论分析需要的数据量少，它根据不完全的信息就能稳定的预测，所以它能挖掘出蕴含在原始数据中的重要信息；但是GM（1，1）模型只能进行短期监测数据的预测，一旦时间过长，预测结果会变得不可靠。

5 结语

利用多学科、多方法的有机结合，进行综合分析和预报，变形监测数据分析方法的深入研究，能更准确的掌握变形的机理，以便确定变形的发展方向与发展速度，为形变体的安全运营提供依据。