基于支持向量机-小波神经网络的PM2.5预测模型

郑国威,王腾军

(长安大学地质工程与测绘学院， 西安 710054)

1 前 言

随着我国工业化、城镇化进程的不断加快，雾霾天气的频发愈演愈烈，引起了国家和人们的高度重视。各级政府都在不断出台“铁腕治霾”，“保护蓝天”等一系列措施。PM2.5作为雾霾的主要成分不仅对人民的生活健康带来严重的威胁，还影响着社会经济的发展。PM2.5因其自身的粒径较小能够长时间停留在大气中，并吸附一些其他的有害物质，被吸入到人体中，很容易诱发呼吸道感染和心血管疾病[1]。PM2.5浓度变化进行有效地监测成为了一个急需解决的问题。因此对PM2.5的准确预测对城市的建设和发展有着重要的意义[2]。

目前，对于PM2.5浓度的预测准确度不高的问题，国内外的学者提出各种来解决这一问题。比较常用的模型有：灰色理论模型[3]、BP神经网络模型[4～6]、SVM[7-8]、随机森林回归分析[9-10]等。传统的BP神经网络容易出现过度拟合、陷入局部最优等缺点。当原始数据存在噪声，灰色模型的预测精度会大大降低。由于不同的模型有着不一样的适用范围和优缺点，如果采用单一模型可能会导致信息的缺失，不能全面反映实际的情况，会造成预测准确度的下降[11]。因此将SVM和WNN的进行组合，结合两个模型优点建立SVM-WNN模型对PM2.5浓度进行预测。

2 支持向量机模型的建立

2.1 支持向量机的基本原理

SVM是Vapnik等人在1995年开发的基于统计学习理论的机器学习方法。该方法以结构风险最小化为基础，能够较好的解决小样本、非线性、高维数等问题，在分类、回归等领域已经得到了很好的应用[12]。

在给定的样本数据{(x1,y1),(x2,y2),…,(xl,yl)}中，xi是输入向量，yi是输出向量。支持向量机回归的基本思想是将样本数据中的输入向量通过一个非线性性变换映射到一个高维特征空间中，然后构造一个最优的线性回归函数：

f(x,α)=ω*x+b

(1)

(2)

约束条件为：

yi-f(xi)≤ξi+ε

(3)

式中：i=(1,2,3……l)，c是惩罚因子。

在求解优化方程时，引入Lagrange函数，分别对式中的变量求导数，令其等于零。可求得f(x)的表达式为：

(4)

引入核函数K(x,xi)=h(x)h(xi),并代入上式中可得：

(5)

式中：α，αi是朗格朗日乘子，g是核函数的参数。由于RBF核函数在实际应用中最为广泛，无论是在小样本、大样本、低维、高维等情况下，RBF核函数都能适用，而且RBF需要确定的参数要少，故核函数K(x,xi)采用径向基函数(RBF)。

2.2 交叉验证和网格搜索算法

交叉验证是检验模型分类效果的一种统计方法，其基本理论是训练的数据划分成K个子集，在训练时每次选取一个子集作为期望输出，其余的K-1个子集作为输入值，一共进行K次，计算 k 组测试结果的平均值作为模型性能指标。该方法不仅可以有效地避免过度拟合的情况，而且提高选取最优参数的效率。

网格搜索算法基本思想是通过设定的惩罚因子c和g来建立起一个二维的网格，通过遍历每一个网格内的点，利用该点对应的值对SVM进行训练，最后得到最优的参数c和g。

2.3 SVM预测步骤

基于网格搜索优化SVM预测模型建立过程如下。

(1)由于样本数据量纲之间存在差异性，采用MATLAB中mapminmax函数对数据进行归一化处理，其公式为：

(6)

(2)利用网格搜索算法选取SVM最优参数c和g。

(3)将最优参数代入到SVM中对训练集进行训练。

(4)利用训练好的SVM模型对测试集数据进行预测评估。

3 小波神经网络

小波神经网络是以BP神经网络为基础，由于小波变换具有较好的时频局部化特点，通过尺度伸缩和平移对数据进行多尺度分析，能够有效提取出原始数据的局部信息，将小波基函数替代原有的隐含层节点Sigmoid传递函数，信号向前传播的同时误差反向传播。对于给定的输入数据xi为(x=1,2,3…k)时，隐含层输出公式为：

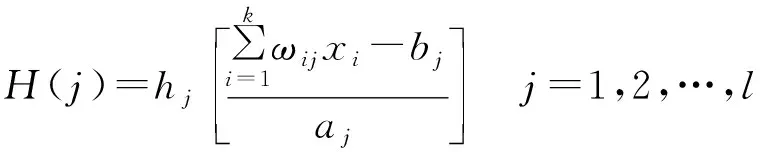
(7)

式中：k表示输入层节点个数；l表示隐含层节点个数；H(j)表示隐含层第j个节点的输出值；hj表示小波基函数；ωij表示输入层和隐含层之间的权值；aj表示小波基函数的的伸缩因子；bj表示小波基函数的的平移因子。小波基函数种类有很多，根据实际情况本文采用的morlet母小波基函数，数学公式为：

(8)

网络输出层计算公式为

(9)

式中：l表示隐含层节点数；m表示输出层节点数；y(s)表示输出层第k个节点的输出值；ωik是隐含层和输出层之间的连接权值；H(j)是第j个隐含层节点的输出值。

小波神经网络采用梯度修正法对权值参数进行修正,进而使输出值不断逼近实际值. 具体步骤如下：

(1)计算预测误差e：

(10)

式中：yn(s)为归一化后的实际值，y(s)为模型预测值。

(2)根据误差e修正对小波基函数系数和网络权值。

(11)

4 支持向量机-小波神经网络模型的建立

PM2.5浓度变化具有一定复杂性，而小波神经网络具有较强的学习能力和逼近能力，利用小波神经网络的优点将SVM预测的残差中的规律性成分进一步提取出来，从而提高模型的预测精度，其流程图如图1所示。组合模型的建立和预测过程如下。

(1)将原始的样本数据经过归一化处理后，利用SVM进行训练并得出预测的结果。

(2)将样本数据和预测值作差得到残差序列。

(3)利用小波神经网络对残差进行修正，得到新的残差序列。

(4)把SVM的预测值和新的残差序列进行补偿运算，得到最终预测结果。

图1 SVM-WNN预测流程Fig.1 SVM-WNN prediction process

5 实验与分析

5.1 数据的收集和预处理

本文采用石家庄市空气质量监测站2018年1月2号到1月22号每小时采集的PM2.5、PM10、SO2、NO2、O3、CO等污染物浓度数据。由于原始样本数据之间的往往具有各自的量纲和单位，这会造成预测的效果不理想。为了解决这一问题，对数据样本进行归一化处理，使得各个指标处于同一个数量级。本文采用的mapminmax函数进行归一化处理。

5.2 组合模型的建立和结果分析

本文取前20天数据作为训练样本，最后一天作为测试集进行预测。按照图1所示的流程图进行预测，将PM10、SO2、NO2、O3、CO作为输入因素，PM2.5浓度作为输出因素。在利用网格搜索算法优化时惩罚参数c的范围是[2-8,2-8]，RBF参数g的范围是[2-8,2-8]，c和g的步进大小为0.8.小波神经网络输入层节点数为5，隐含层节点为9，构建一个5-9-1的网络模型。利用建立的单一的模型和组合模型分别对测试集数据进行预测，预测的结果和实际值的对比情况如图2所示。

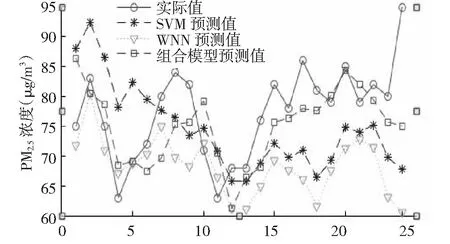
图2 3种模型预测效果对比图Fig.2 Prediction of the effect of the two models compared

计算模型预测的相对误差，绘制如图3所示。

图3 三种模型预测相对误差图Fig.3 Relative error of prediction of three models

由图2和图3可知，SVM预测最大的相对误差为28.7%，最小的相对误差为2.2%，平均相对误差为11.5%；小波神经网络预测最大的相对误差为36.2%，最小的相对误差为0.4%，平均相对误差为12.0%；组合模型预测最大的相对误差为21.0%，最小的相对误差为0.2%，平均相对误差为7.3%。相对误差大于10% 3个模型分别占比62.5%、54.1%、33.3%。3种模型相比，组合模型预测的精度更高且稳定性更好，预测的整体效果要优于单一模型。

6 结 论

针对PM2.5浓度预测的复杂性，采用网格搜索算法对SVM模型进行参数寻优，小波神经网络把神经网络的自学习特点和小波的局域特性结合起来对SVM预测的残差进行修正，尽可能的提取残差中的确定性因素，从而提高预测精度。此外，论文中未加入降水，风速、湿度等气象因子，在今后的研究中应该考虑更多的影响因素来全面的反应PM2.5浓度变化的规律，从而建立起更加精确的预测模型。