重力平衡式手术显微镜机架平衡机构设计与研究

，

(江苏科技大学机械工程学院，江苏 镇江 212003)

0 引言

随着显微外科技术的不断发展，手术显微镜已经广泛应用于各类手术中[1]。手术显微镜机架作为手术显微镜的重要组成部分，用于支撑显微镜并提供手术过程中显微镜的移动调整功能。其性能是至关重要的，影响着医生的工作效率，以及操作时的舒适性和便捷性。

手术显微镜机架的平衡方式一般分为3种，即机械弹簧平衡、气动弹簧平衡和重力平衡。机械弹簧及气动弹簧都存在同样的问题，就是平衡区间内平衡力的变化是非线性的，需要对转动关节施加较大的阻尼来保证在任意位置的平衡[2]。这不仅增加了移动显微镜的阻力，也限制了手术显微镜机架的伸展范围。平衡机构是重力平衡式手术显微镜机架的关键部分，它利用了杠杆平衡的原理，依靠配重来平衡显微镜的重量[3-5]。当显微镜增减附件后，可以移动配重进行平衡调节。如今，重力平衡在国外已经成为了一种发展潮流，蔡司和徕卡先后将重力平衡应用在高端手术显微镜机架上，但国内目前尚未推出重力平衡式手术显微镜产品。

针对上述问题，以一种新型重力平衡式手术显微镜机架(下文简称机架)为研究对象，对机架的平衡机构进行设计和分析研究[6]。

1 机架的组成

机架的整体结构如图1所示，主要由底座、配重、电控箱、悬臂、主支撑臂、配重臂和头部机架等组成。该机架可以提供足够的伸展空间，实现显微镜的大范围移动。

图1 机架的整体结构

机架共有6个转动关节，类似于关节机器人的“腰”、“肩”、“肘”和“腕部”。但与机器人不同的是，机架所有转动关节都采用失电式电磁锁，失电锁紧,得电松开，通过末端手动引导的方式来调整位姿。

2 平衡机构设计与计算

2.1 平衡调节方案设计

平衡机构是实现重力平衡的关键部分，能够使显微镜在接近失重的状态下移动。双轴调节的平衡机构由支撑框架和配重组成，如图2所示。首先,从整体上来看，支撑框架由2组平行四边形构成，采用这种结构形式可以提高平衡机构整体的稳定性，增加其强度和刚度。其次，配重用于维持整体质心C与支点O的重合，实现整体的平衡，使显微镜移动省力。当显微镜根据手术需要增减一些附件(包括助手镜、CCD摄像系统等)后，整体质心会沿水平和垂直方向发生偏移，所以需要左右移动的配重G1和上下移动的配重G2来共同调节，使质心回到支点，保持重合。

双轴调节可以保证整体质心与支点是重合的，能够实现完美的平衡，但利用电机控制2个配重在不同的轴线上运动，必然会增加结构的复杂性。为了使平衡机构简单紧凑，考虑在图2基础上进行改进。

图2 双轴调节的平衡机构

由图2可知，显微镜与支点之间的水平距离比垂直距离大很多。所以，当显微镜增减附件后，引起整体质心的偏移是以水平方向为主，垂直方向只有少量的偏移。因此，去除垂直方向的配重G2，只保留G1，采用图3所示的单轴调节的平衡机构。该方案的结构更为简单，控制也很方便。但是，由于缺少了竖直方向的配重，无法消除整体质心与支点之间沿竖直方向的少量偏移，只能消除沿水平方向的偏移。因此，整体质心(图3中C点)与支点无法重合，而是在同一竖线上，只能达到近似平衡。当平衡机构发生转动时，会产生不平衡力矩[7]，需要对这一力矩进行校核。

图3 单轴调节的平衡机构

2.2 平衡调节参数计算

该机架采用了单轴调节的平衡机构，仅依靠水平移动的配重进行平衡调节，需要进一步计算出配重的质量以及它的调节距离。

如图4所示，以支点O为原点建立平衡机构的坐标系。由于单轴调节实现的是近似平衡，只能调节整体质心与支点沿水平方向的偏移为零，即整体质心的横坐标为零。根据质心坐标公式得到近似平衡的条件为：

(1)

又因为∑mi≠0，所以式(1)简化为：

∑mixi=0

(2)

Xc为整体质心的横坐标；xi为第i部分质心的横坐标；mi为第i部分的质量。

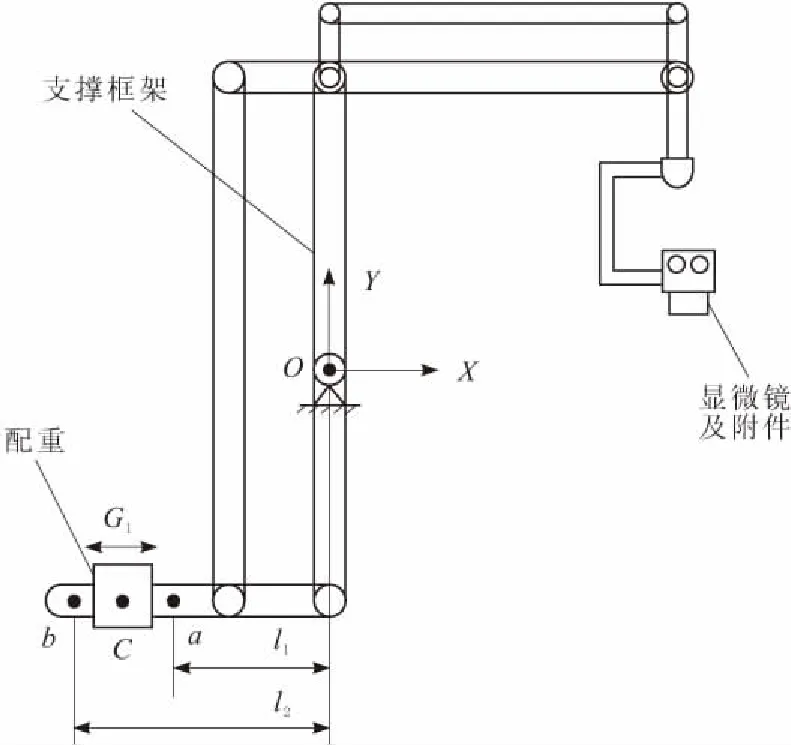
图4 单轴调节计算

将图4整体看成3部分组成，分别是显微镜及其附件、支撑框架和配重。其中，显微镜及其附件的质量是可变的，在8～12 kg之间，增量Δm不超过4 kg。在2种极限情况Δm=0 kg，Δm=4 kg时，也能达到近似平衡，所以利用近似平衡条件式(2)对2种情况进行计算，求出配重质量以及它的调节范围。

如图5所示，根据平衡机构的三维模型，通过SolidWorks质量属性分别获取Δm=0 kg，Δm=4 kg时3部分的质量和质心坐标，如表1和表2所示。

图5 平衡机构三维模型

表2 各部分质心坐标

根据表1和表2，由式(2)可得：

m1x1+m2x2+m3x3=0

(3)

当Δm=0 kg时,显微镜及其附件的质量最小，配重质心C在最右端a处；由于配重臂长度及其结构的限制，经设计取l1=450 mm，然后将表1和表2中的第1行数据代入式(3)，计算得到配重质量m3=47.3 kg。

当Δm=4 kg时,显微镜及其附件的质量最大，配重质心C在最左端b处。将表1和表2的第2行数据代入计算得到l2=535.7 mm。a点与b点之间的长度，也就是调节距离。调节距离S=l2-l1=85.7 mm。

通过上面的计算，粗略地得到了平衡调节的相关参数，即配重的质量m3=47.3 kg，调节距离S=85.7 mm，能够满足使用要求。

2.3 不平衡力矩校核

单轴调节的平衡机构可以实现近似平衡，但是整体质心与支点沿Y方向还存在少量偏移。所以，一旦平衡机构发生转动，整个系统的重力就会产生额外的力矩。为了使显微镜移动省力，锁紧可靠，就需要对该不平衡力矩进行校核。

首先，计算2种极限情况Δm=0 kg，Δm=4 kg时整体质心的纵坐标Yc1，Yc2，就得到了整体质心的2个极限位置。根据质心公式：

(4)

Yc为整体质心的纵坐标；yi为第i部分质心的纵坐标。

代入表1和表2的数据计算得：

T=(m1+m2+m3)g×r×sinθ

(5)

计算得到最大不平衡力矩Tm=5.8 N·m。而电磁锁提供的锁紧力矩一般为40～50 N·m，可以有效锁紧，而且，当不平衡力矩作为移动阻力时，并不是很大，可以轻松地移动显微镜，满足使用要求。

图6 不平衡状态简图

3 平衡机构分析与优化

3.1 平衡机构的有限元分析

有限元分析包括静力分析、模态分析和疲劳分析等。其中，静力分析是基础，用于获得结构在静载荷作用下的响应，不用考虑惯性和阻尼的影响，只为求得结构的位移、应力、应变和约束反力等未知量。

3.1.1 几何模型的简化

当主支撑臂与竖直方向的夹角达到最大，为50°时，且其他两臂保持水平，此时平衡机构所承受的弯矩最大，所以对该位姿进行分析。由于平衡机构相对复杂，零部件数量较多，为了能够得到简洁有效的有限元模型，提高有限元分析的可行性和效率[8]，需要对其进行必要的简化。简化方法如下：

a.移除模型中对结构性能影响较小的特征，如倒角、圆角和螺纹孔等。

b.去除臂内质量较小的零件，包括轴承、圆螺母和螺钉等，但为了保证分析精度，较大的零件如带轮、电磁铁等，则不能忽略它们的质量，将它们简化成质点，用质量单元来模拟。

c.去除配重、头部机架和显微镜，将它们简化成外力进行施加。

简化后的平衡机构如图7所示。

图7 平衡机构简化后的模型

3.1.2 有限元模型的建立

将简化后的几何模型导入ABAQUS中，添加各个零部件的材料属性。平衡机构具体的材料属性如表3所示。

表3 零件材料属性

网格平均尺寸为8 mm，单元数为127 718，节点数为217 135。网格划分结束后，继续完成以下几个步骤：

a.添加各零部件之间的连接关系，如接触、绑定等。

b.添加边界条件，由于实体单元不考虑转动自由度，所以只需约束支点处孔内壁的U1，U2，U33个方向的平动自由度。

c.添加整个平衡机构的重力，重力加速度为-9.8 m/s2。

d.将配重、头部机架和显微镜的重量等效为均布力进行施加。

3.1.3 求解及结果分析

利用ABAQUS进行求解，得到位移和应力云图分别如图8和图9所示。

图8 位移云图

由图8可知，最大位移发生在前支架处，最大值为4.475 mm。由于前支架处于结构的末端，因此最大位移量是由各部分叠加而得的，在允许范围内，刚度满足要求。

图9 应力云图

由图9可知，应力较大区域主要分布在主支撑臂上部及悬臂根部附近，符合实际情况。最大应力值为29.05 MPa，位于悬臂根部，远低于2A12铝合金的屈服强度345 MPa，因此强度也符合要求。

3.2 平衡机构的优化

由上面的分析可知，平衡机构的强度和刚度都满足要求，最大应力远小于材料的屈服强度。因此，可以对结构进行优化来减轻质量。由于配重臂及主支撑臂内部结构复杂，优化难度较大，所以针对图10所示的悬臂和拉杆做2点改进：

a. 悬臂的厚度由6 mm改为4 mm。

b. 拉杆由实心杆改用无缝钢管。上拉杆直径为18 mm，厚度为3 mm；下拉杆直径为25 mm，厚度为4 mm。

对改进后的平衡机构再进行有限元分析，求解结果如图11和图12所示。改进前后参数对比如表4所示。

图10 平衡机构改进处

图11 改进后的位移云图

图12 改进后的应力云图

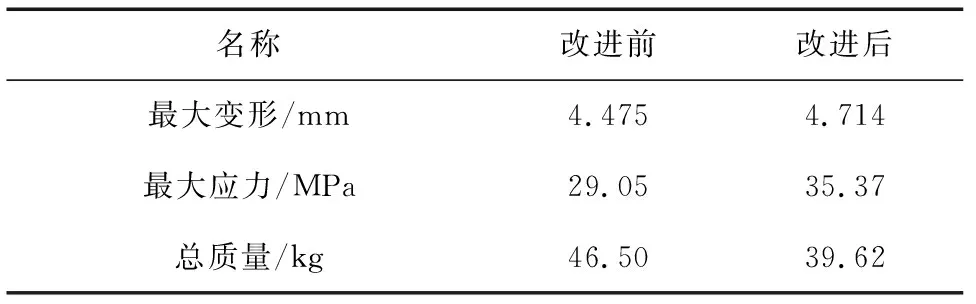
名称改进前改进后最大变形/mm4.4754.714最大应力/MPa29.0535.37总质量/kg46.5039.62

由表4可知，改进后平衡机构的最大变形和最大应力都有所增加，但仍符合设计要求，满足刚度、强度，以及机架整体精度要求。改进后平衡机构的质量为39.62 kg，比优化前减轻了14.8%，实现了轻量化。

4 结束语

针对一种新型重力平衡式手术显微镜机架,对其平衡机构进行设计和分析优化,得到以下几个结论：

a.采用单轴调节的平衡机构，简单紧凑，同时具备良好的平衡性能，计算得到的最大不平衡力矩，小于电磁锁的锁紧力矩Tm=5.8 N·m，可以有效锁紧。此外，克服不平衡力矩对显微镜进行移动也比较轻松。

b.利用ABAQUS对平衡机构进行有限元分析，得知在危险位置时结构的应力及变形都在允许范围内，满足强度刚度要求，验证了平衡机构采用双平行四边形框架的合理性。

c.在保证强度刚度满足要求的前提下，对平衡机构进行优化改进。改进后，质量相比之前减轻了14.8%，实现了轻量化。