一种基于单换能器的超声离合器的设计及性能分析

， ，， ，

(四川大学制造科学与工程学院，四川 成都 610065)

0 引言

离合器被广泛用于运动系统中驱动轴与从动轴之间的分离和接合，甚至用于转速的控制，传统的离合器由于结构复杂、尺寸较大、需要润滑，以及磁粉离合器会造成严重的电磁干扰(EMI)等缺陷，限制了其在更广泛领域的使用[1-2]。近年来，近场声悬浮(NFAL)以其无接触、低磨损、无润滑等优点成为国内外学者的研究热点。国内外众多学者研究了近场超声悬浮在非接触式线性运动领域的应用，如非接触式直线导轨、非接触式运输系统、非接触式推力轴承[3]。目前，将近场超声悬浮技术运用于离合器的研究还相对较少。2004年，Chang[4]等人旨在设计一种无EMI的离合器，建立了双换能器离合装置，通过实验获得2个换能器耦合下不同工作形式的输出转速，表明至少有一个换能器达到谐振时从动轴转速随激励电压的增大而减小，甚至停止转动；2008年，Chang[5]等人利用2个薄片压电蜂鸣器作为驱动元件和从动元件建立了一种对称式压电式离合器，对不同频率和电压下驱动轴与从动轴的转速特性进行了研究；Cheng[6]等人采用双换能器和摩擦盘构成了纵弯耦合模型，研究了纵向和弯曲振动耦合对离合器输出性能的影响。

在以往关于超声离合器的研究中，大多数学者都采用双换能器的对称结构，研究了电压与转速的关系。为减少或克服上述传统离合器的缺陷，获得一种结构更简单紧凑、成本更低廉、体积尺寸更小型化的超声离合器，提出了一种基于单换能器的新型超声离合器，分析了近场超声悬浮理论下超声离合器的作用机理，建立了换能器模型，设计了一种提供预紧力新结构。搭建超声离合器的原型机，实验研究原型机的转速、转矩输出特性，验证单换能器超声离合器的可行性。

1 近场超声悬浮

典型的近场超声悬浮如图1所示。该简化模型由振动板和悬浮板构成。假设悬浮板是刚性的，其为声源声波的反射板，在振动板和悬浮板之间的间隙中产生声场，振动板和悬浮板之间的悬浮高度通常是微米级的，远小于空气中的声波长。因此，当振动板高频振动时，薄的气膜在间隙中迅速压缩和膨胀，由于2个表面之间的气膜所具有的二阶效应，1个周期内间隙中的平均压力高于环境压力，因此对悬浮板产生了向上的正压力[3]。纵振声源以u(t)=u0sin(ωt)做简谐运动，则理想气体中的瑞利辐射声压计算模型为[7]：

图1 近场超声悬浮示意

(1)

E表示能量密度，其表达式为：

(2)

k为波数，表达式为k=ω/c=2πf/c；P为辐射压力；γ为气体的比热比；ρ0为气体的密度；c为声音在介质中的传播速度；u0为振子的振动幅度；h为悬浮高度。由于悬浮高度h是微米级的，即kh=2πh/λ1，所以可以近似认为sin(kh)≅kh，则式(1)可简化为：

(3)

因此，当h,γ,ρ0,c为常数时，辐射声压随着振幅的增大而增大，当声辐射压对悬浮板的推力大于等于悬浮板上向下的作用力时，即可产生悬浮现象。

2 结构与工作原理

2.1 超声离合器的结构

基于单换能器的超声离合器的结构如图2所示。该离合器驱动端与电机相连，主要由超声换能器、换能器支撑架、导电滑环和轴承组成。换能器固定在支撑架上，通过导电滑环旋转供电。从动端与负载相连，主要由从动轴、预紧装置和输出轴组成。预紧装置是一个给从动轴提供预压力，并且能向负载传递转矩的机械组件，是该超声离合器必不可少的关键部分。轴承为超声离合器提供了支撑，并固定了驱动端和从动端的相对位置，保证离合器的正常运转。

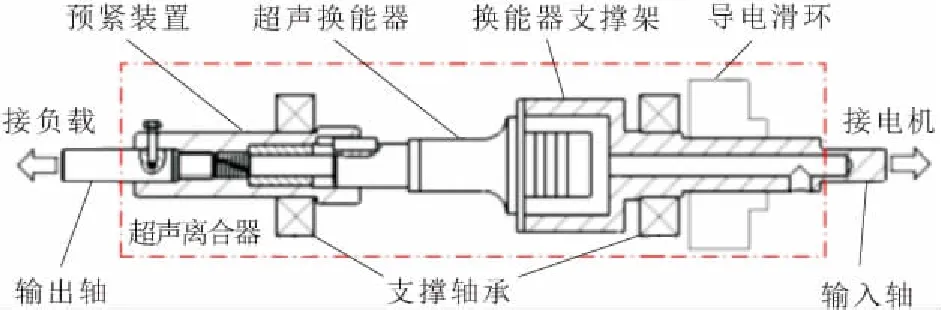
图2 超声离合器结构

2.2 工作原理

超声离合器工作原理如图3所示。当超声换能器未施加电激励时，超声换能器不产生振动，驱动端和从动端在弹簧预紧力的作用下紧密贴合，处于未分离状态，两者在摩擦力矩的作用下同步旋转，如图3a所示。当给超声换能器施加电激励功率较小时，驱动端的超声换能器产生的悬浮力不足以完全克服输出端弹簧的预紧力，此时驱动端与从动端处于半联动状态，驱动端带动从动端旋转，弹簧预紧力产生的摩擦力矩不足以带动从动端同步旋转，两者差速转动，如图3b所示。当给超声换能器施加的电激励产生的悬浮力比从动端的弹簧预紧力大时，从动端与驱动端处于分离状态，从动端由于悬浮高度的增加，弹簧预紧力增大且悬浮力减小而达到平衡态，两者由于悬浮间隙的存在而处于分离状态，如图3c所示。

图3 超声离合器工作原理

2.3 超声换能器的设计

所需超声换能器应该获得尽可能大的振幅，因此选用阶梯状前盖板，此外，为获得较大的前后盖板位移振幅比，减小能量损耗，提高换能器的能量传递效率，前盖板材料采用硬铝，后盖板采用45#钢。结构采用4片锆钛酸铅压电陶瓷(PZT-8)，设计功率和频率分别为500 W和28 kHz。根据传输矩阵法[8]和夹心式压电换能器的相关设计理论[9]，计算该模型初始尺寸。利用ANSYS进行优化，最终获得图4所示的换能器结构及最佳尺寸。为减小应力集中，在前盖板大端与小端的连接处应采用圆弧过渡，根据文献[10]查表可知最佳过度圆弧的半径R=12 mm。利用优化所得最终尺寸对换能器建立模型，再对该模型进行模态分析，可得如图5所示的位移云图。其纵振频率为27.969 kHz，与设计频率28 kHz十分接近，相差0.11%，满足设计要求。

利用阻抗分析仪PV80A对设计加工的超声换能器进行阻抗测试。从测试结果可以知道，超声振动子的谐振频率为27.753 kHz，跟设计频率28 kHz有0.88%的误差，造成偏差的原因主要是材料性能参数、制造误差等。该误差在超声电源的工作范围内，对超声换能器的正常起振工作不会产生影响。

图4 超声换能器结构

图5 换能器优化模态

2.4 预紧装置的设计

以往大多数关于超声离合器的研究基本都采用弹簧提供预压力进行预紧，但是从目前已有的预紧方式来看，存在预紧力不可调和尺寸过大等缺点，因此设计一种尺寸更小、结构更紧凑、预紧力可调的预紧装置。

如图6所示，预紧装置主要由从动轴、从动轴套、输出轴、预紧螺栓、预紧弹簧、直线轴承和键等组成。从动轴套为空心套筒，其大端的孔壁上开有键槽，用于与插装在该孔中的从动轴进行键连接；其小端与键槽同一轴线上钻有螺纹孔，用于与插装于该孔中的输出轴进行螺栓连接，这2种连接方式都起到传递转矩的作用。预紧螺栓、预紧弹簧和直线轴承内置于从动轴套内。预紧螺栓和孔内螺纹配合用于调节预压力。预紧弹簧用于产生预压力，处于放松状态时两端分别与预紧螺栓和从动轴接触。直线轴承与轴孔过盈配合用于从动轴的定位和导向。调节预紧螺栓可以改变预紧弹簧的弹簧力，从而实现预紧力可调。从动轴套与从动轴和输出轴的连接实现了转矩的传递。因此这种预紧装置既能实现预紧力可调，又使得结构更加紧凑。

图6 预紧装置结构

3 实验研究

为了检验超声离合器的有效性，搭建了图7所示的超声离合器实验平台。平台包含了以下结构：电机及其调速系统；导电滑环；超声离合机构；动态扭矩传感器，用于转速、扭矩的实验数据采集；2个联轴器，其中联轴器1用于超声离合机构输入端与电机连接，联轴器2用于连接超声离合机构输出端和动态扭矩传感器。

实验平台的实物如图8所示。本次实验通过改变驱动换能器的超声电源输出功率，来实现超声换能器振幅的改变。通过多组实验来确定几种不同工作条件下原型机的输出转速和扭矩大小，几种工作条件分别是：未施加超声不带负载；未施加超声带负载；施加超声不带负载；施加超声带负载。为了进一步研究该超声离合器的性能，实验选取500 r/min和800 r/min作为输入转速，分析不同转速下该离合器的减速比与超声电源输出功率的关系。采集超声电源输出功率在50 W，100 W，150 W，200 W，250 W，300 W，350 W，400 W下，超声离合器的输出转速和扭矩数据，并对比空载与带负载2种情况下扭矩和转速的输出大小。500 r/min下超声电源功率与超声离合器输出转速、扭矩的关系如图9所示；电机转速为800 r/min下超声电源功率与超声离合器输出转速、扭矩的关系曲线如图10所示；超声电源功率与超声离合器减速比之间的关系曲线如图11所示。

图7 超声离合器实验平台

图8 超声离合器实验平台实物

由图9a和10a可知，随着超声电源功率的增加，超声离合器从动端输出转速逐渐下降，当超声电源的输出功率达到0.35 kW时，超声离合器从动端和驱动端分离，形成近场悬浮，因而输出速度为零，且在负载条件下因为阻碍力矩的存在，带载的转速下降比空载的快。在超声电源输出功率增大的过程中，由于超声振动产生的超声减摩效应[12]，导致超声离合器输出端转速与电机输入转速不同步，超声减摩的效应随着超声电源功率的增大而增强，直至产生近场悬浮。

分析图9b和10b可知，在空载条件下，由于超声离合器输出端没有负载，因此扭矩传感器没有信号输出，扭矩为零；在有负载条件下，随着超声电源功率的增加，输出端扭矩随之下降，在功率达到0.35 kW时，从动端和主动端分离，形成近场悬浮，此时输出扭矩为零。此外，实验中通过使超声离合器输出端处于制动状态，测得在转速为500 r/min时，超声离合器的过载扭矩为0.39 N·m，转速为800 r/min时的过载扭矩为0.42 N·m。

图9 500 r/min时输出转速、扭矩与超声电源功率关系

图10 800 r/min时输出转速、扭矩与超声电源功率关系

图11 减速比与超声电源功率关系

由图11可知，在施加超声激励的工作条件下，无论是空载还是带负载，随着驱动换能器的超声电源功率的增大，超声离合器的减速比减小，不同输入转速下的减速比不同，但十分接近，具有相似的变化趋势。对于特定输入转速下该离合器的调速控制，可以利用牛顿插值法得到以下近似的计算公式，为调节超声离合器输出转速提供了近似参考。

当转速为500 r/min时，有：

n1=-2.41×10-15p8+4.01×10-12p7-

2.72×10-9p6+9.73×10-7p5-1.94×

10-4p4+0.021p3-1.17p2+24.26p+500

(4)

当转速为800 r/min时，有：

n2=-2.17×10-15p8+3.75×10-12p7-

2.65×10-9p6+9.80×10-7p5-2.02×

10-4p4+0.022p3-1.28p2+26.51p+800

(5)

n1，n2为超声离合器输出转速；p为驱动换能器的超声波电源输出功率。

4 结束语

通过分析超声振动的近场特性，研究超声近场悬浮力的计算模型，确定对近场悬浮力的影响因素；基于近场悬浮的机理，设计并制造了一种结构紧凑、预紧力可调、谐振频率为27.75 kHz的单换能器型超声离合器，建立了超声离合器实验平台。通过实验数据，分析了超声离合器输入转速为500 r/min和800 r/min下超声电源输出功率与转速、扭矩以及减速比的关系，确定了设计的超声离合器实现分离的超声电源输出功率为0.35 kW，验证了单换能器超声离合器的可行性和有效性；利用牛顿插值法获取了空载时超声离合器输出转速与超声电源输出功率的近似计算关系式，为调节超声离合器的输出转速提供了参考。