结合量子技术和FCM的猪肉颜色分级研究
孙 宝 杨世恩
(1.西南科技大学计算机科学与技术学院 四川绵阳 621010; 2.西南科技大学国家大学科技园 四川绵阳 621010)
猪肉是城乡居民日常生活的必需品,自进入21世纪以来,随着我国经济快速增长,国人生活水平迅速提高,消费观念从数量型向质量型转变。人们对猪肉已经不限于满足数量上的基本需求,而且也要吃的放心,主要体现在提高质量、确保安全、调整结构、增进健康和保护生态环境。因此,研究猪肉品质在线无损检测技术并将其引入到普通群众的生活中具有重要的现实意义。
猪肉的颜色特征是其外观品质分级检测的重要指标,依据我国农业部标准,把猪肉颜色等级分为3个等级,从高到低分别为1级、2级、3级。目前国内常见的猪肉颜色分级检测方法主要有感官标定法和标准的理化实验法,但是这些方法都存在主观意识强、时间过长影响检测结果以及成本过高的缺陷。本研究基于机器视觉技术,结合量子思想衍生的中值滤波算法和FCM对猪肉颜色进行分级检测研究,对猪肉品质在线无损检测技术有一定的现实意义。
1 改进的中值滤波算法及仿真结果
1.1 噪声的产生以及传统解决办法
基于项目需求,本研究采集了约600张猪肉图像,其分级情况如图1所示。图1(a)中为PSE肉,这类肉颜色苍白、组织松软、表面暗淡无光泽,归为1级;图1(b)为RFN肉,这类肉为正常肉归为2级;图1(c)为 DFD肉,这类肉干燥、色泽暗黑、表面比较硬,归为3级。

图1 猪肉颜色等级图Fig.1 Pork color grade map
由于猪肉表面污渍和周围环境光源等原因,在分级之前必须要对这些猪肉图像做去噪预处理,以提高项目的准确性。 目前最主流的去噪方法是中值滤波,简单地说就是把摸板内的像素点按照灰度值进行排序,中值即作为模板中心像素点的像素值,此种方法有较好的去噪效果[1]。但这种方式存在着两个缺点,一是当中心像素点不是噪声点时或者中值像素点离中心像素点较远,这种替换不可避免的损坏图像细节;二是当摸板内噪声像素点大于或等于模板总像素点时此时去噪能力基本丧失。
针对以上问题,本文借鉴量子理论思想对传统中值滤波进行改进,并采用仿真方法比较改进算法和传统方法在去噪能力、保留图像细节等方面的优劣。
1.2 量子比特
比特是数据存储的最小单位,其状态处于0或1。在量子系统中,与经典比特对应的是量子比特[2]。与经典比特不同的是,由于量子叠加态的原理,一个量子系统的状态可以通过两个标准的正交基态的叠加来完全描述,它可以同时处于|0>和|1>之间,即
|φ>=a|0>+b|1>
(1)
式中,a和b是复系数,表示基态的概率幅,a2和b2分别表示量子系统经过测量后出现|0>和|1>的概率。若|0>和|1>是相互正交的,则a和b满足归一化条件,即
a2+b2=1
(2)
一个系统|φ>若由n个子系统构成,子系统的状态为{φ1,φ2,φ3,……,φn},根据量子力学第四假设,该复合系统状态为[3]:
|φ>=|φ1>⊗|φ2>⊗|φ3>……⊗|φn>=
(3)
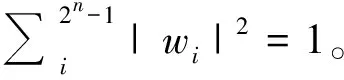
1.3 灰度图像的量子比特表示
设f(m,n)为一副数字图像,(m,n)∈z2。f(m,n)是归一化处理后的图像,其像素值大小范围为[0,1],f(m,n)表示图像在(m,n)处的灰度值。根据式(1)可以将灰度图像表示为量子比特的形式:
(4)
这里,|0>和|1>对应着经典图像的黑点与白点,对应着二值化图像中的“0”或“1”。1-f(m,n)表示在图像位置为(m,n)处的像素值取0的概率,f(m,n)表示在位置(m,n)处图像的像素值取1的概率,显然它们满足归一化条件[4]。
在这里需要介绍的是量子Hadamard变换,根据量子力学的第三和第四假设,利用单比特量子门Hadamard(简记为H)作用于式(1),得:
(5)
其中H为:
(6)
1.4 改进传统中值滤波介绍与仿真结果
下面以尺度3×3的图像窗口为例,设中间像素(m,n)的值为fm,n,邻近像素值为fi,j,m-1≤i≤m+1,n-1≤j≤n+1,如图2所示。

fm-1,n-1fm-1,nfm-1,n+1fm,n-1fm,nfm,n+1fm+1,n-1fm+1,nfm+1,n+1
图2图像3×3子块
Fig.2 Image 3×3 sub-blocks
把3×3的图像窗口作归一化处理后,黑点和白点分别用量子的叠加形式来表示,利用公式(5)-公式(6)对公式(4)进行量子Hadamard门操作,得到式(7)。
(7)
根据量子理论思想坍缩原理,若对图像中某点经过Hadamard变换后的新态矢H|fm,n进行测量操作,则得到|0>的概率为:
(8)
由式(8)可看出,当图像中该点为0或者1(即“黑点”或“白点”)时,此时得到|0>的概率为0.5。在0和1之间的任何一个数值都会使此式的值大于0.5,因此,利用这一特征可以排除图像中明显的椒盐噪声。若以0.5为阈值对测量后的各个像素点进行二值化处理,则各像素点在取得|0>的概率大于0.5时赋予1,等于0.5时赋予0。则图像灰度值为0和1的像素点均转化为0,此时把剩下为1的点构造一个新的模板并把像素点按照从小到大排序,其中值即是中心点的新值。在这里需判断模板中心像素值二值化处理后是不是0,不是则认为该点未受到噪声影响,不做任何处理。
以2级猪肉图像为实验对象,对其加入强度为0.1,0.2,0.3,0.4倍的椒盐噪声,分别使用传统中值滤波、加权中值滤波和本文所提出的改进算法对其进行去噪处理,仿真结果如图3-图6所示。仿真表明本文改进的中值滤波改进算法去噪效果优于传统中值滤波和加权中值滤波,特别在噪声强度为0.3以上的时候,效果更加明显。而且其设置的条件滤波方式也能保证图像不会大幅度失真,尽可能地保留图像的细节特征。
2 猪肉最大连通肌肉区域提取
猪肉图像(以3级猪肉图像为例)经过一系列的预处理以及上面改进算法后得图7,白色的主要为脂肪和背景区域,红色的主要是肌肉区域,两者之间存在明显的颜色差异,实验表明仅利用最大类间方差自适应阈值法进行肌肉与脂肪的分割并不能分割出满意的效果,而 FCM(Fuzzy C-Means)是一种优秀的聚类算法,理论成熟应用广泛(本文将不在予以阐述)[5],因此本文将采取FCM进行脂肪与肌肉的分离,在利用孔洞填充、形态学操作最终把最大连通肌肉区域提取出来,效果如图8所示。

图3 0.1倍噪声情况下各算法结果Fig.3 Results of each algorithm under the condition of 0.1 times

图4 0.2倍噪声情况下各算法结果Fig.4 Results of each algorithm under the condition of 0.2 times

图5 0.3倍噪声情况下各算法结果Fig.5 Results of each algorithm under the condition of 0.3 times

图6 0.4倍噪声情况下各算法结果Fig.6 Results of each algorithm under the condition of 0.4 times

图7 预处理后的图像Fig.7 Pre-processed image

图8 FCM分割的图像Fig.8 Image processed by FCM
由图8可知,肌肉像素点置为0,脂肪的像素点置为1。要想得到原始图像的肌肉区域,只需将图8进行一次取反操作,而后在与原始彩色图像进行相乘的操作即可得到彩色最大连通区域肌肉图像,如图9所示。

图9 分割得到的肌肉图像Fig.9 The final muscle image
3 猪肉图像颜色特征的提取
根据上面介绍的最大连通肌肉提取算法,从600张样本集中随机地从每个级别中抽取20张猪肉图像,共计60张进行实验。在得到只包含肌肉像素(其余像素点的灰度值为0)的图像后,即可提取猪肉颜色特征R,G,B各分量的平均值MR,MG,MB和标准差DR,DG,DB。
对各等级猪肉图像颜色特征分量进行统计分析,计算出各个颜色特征参数的均值以及分布范围,如表1所示。可以看出,随着等级的增加,MG和MB在逐渐减小,而对于MR,DR,DG和DB则呈现无规律变化。
4 猪肉图像等级模型的建立
为了更直观的了解MG,MB和颜色等级之间的关系,做出MG,MB与颜色等级之间的简单线性回归曲线,如图10所示,图像颜色特征参数MG,MB与颜色等级呈显著的线性关系[6]。因此,以这两个参数为自变量,颜色等级作为因变量进行多元线性逐步回归分析,建立颜色等级与颜色特征参数之间的数学模型。首次得到残差图如图11所示。
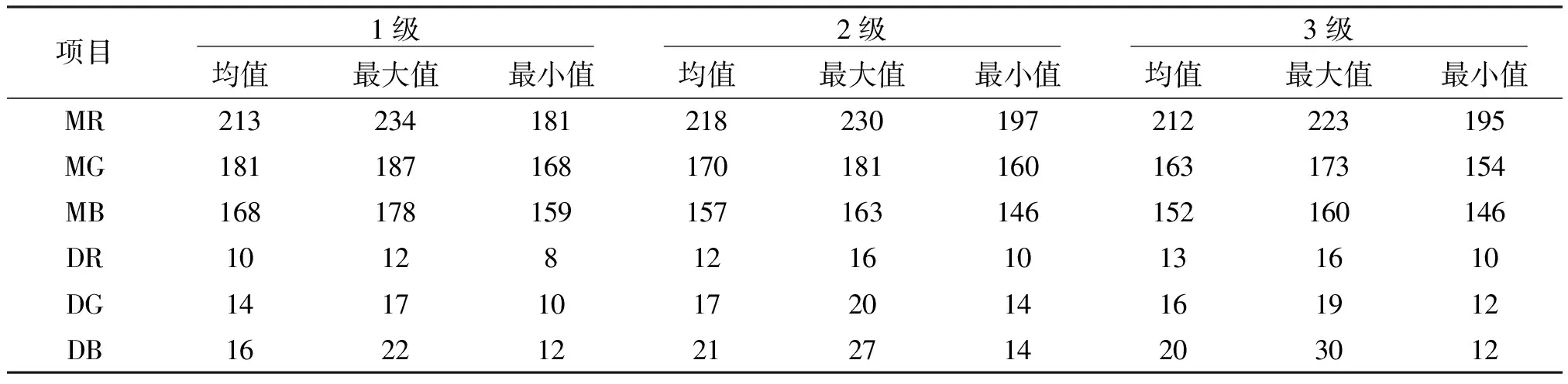
表1 颜色特征参数统计结果Table 1 Statistical results of color feature
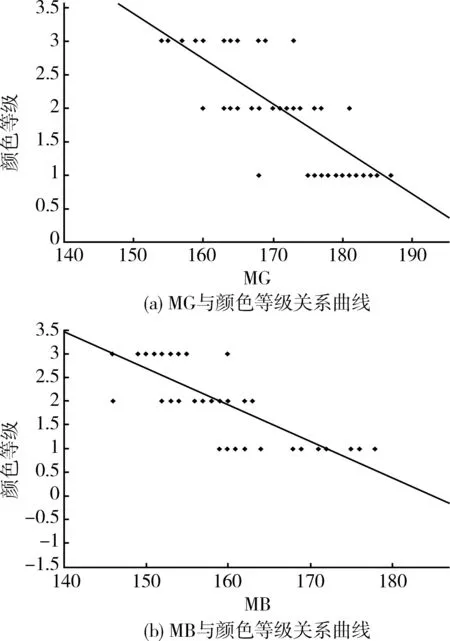
图10 MG,MB与颜色等级关系曲线Fig.10 Relation chart between MG, MB and color grade

图11 残差图Fig.11 Residual map
从图11可以看出,大部分数据的残差离零点均比较近,且残差的置信区间均包含零点,少部分可视为异常点(置信区间不包含零点)[7],造成这个现象的原因主要有二,其一是图像采集时,猪肉表面的水分容易引起反光造成图像颜色差异较大,其二是人工标定时专家在对猪肉定级时难免会有一定的人为误差。在剔除这些异常点后得到一个新的残差图如图12所示,可知此次全部残差的置信区间都包含零点,且返回值中相关系数r高达0.863 1、与显著性概率相关的p是0.000 0,由此可见此次求出的线性回归方程是有意义的[8],具体参数返回值如表2所示。
根据表2可知,此次得到的多元线性回归方程为PG=15.6503-0.0346MG-0.0482MB(PG表示猪肉颜色等级),用此方程对剔除异常点之后的数据进行颜色等级的自动判别,结果如表3所示。

图12 剔除异常点之后的残差图Fig.12 Residual map after eliminating the abnormal points

b 常数MG系数MB系数 stats r2Fpf15.650 3-0.034 6-0.048 20.863 1104.426 00.000 00.123 1
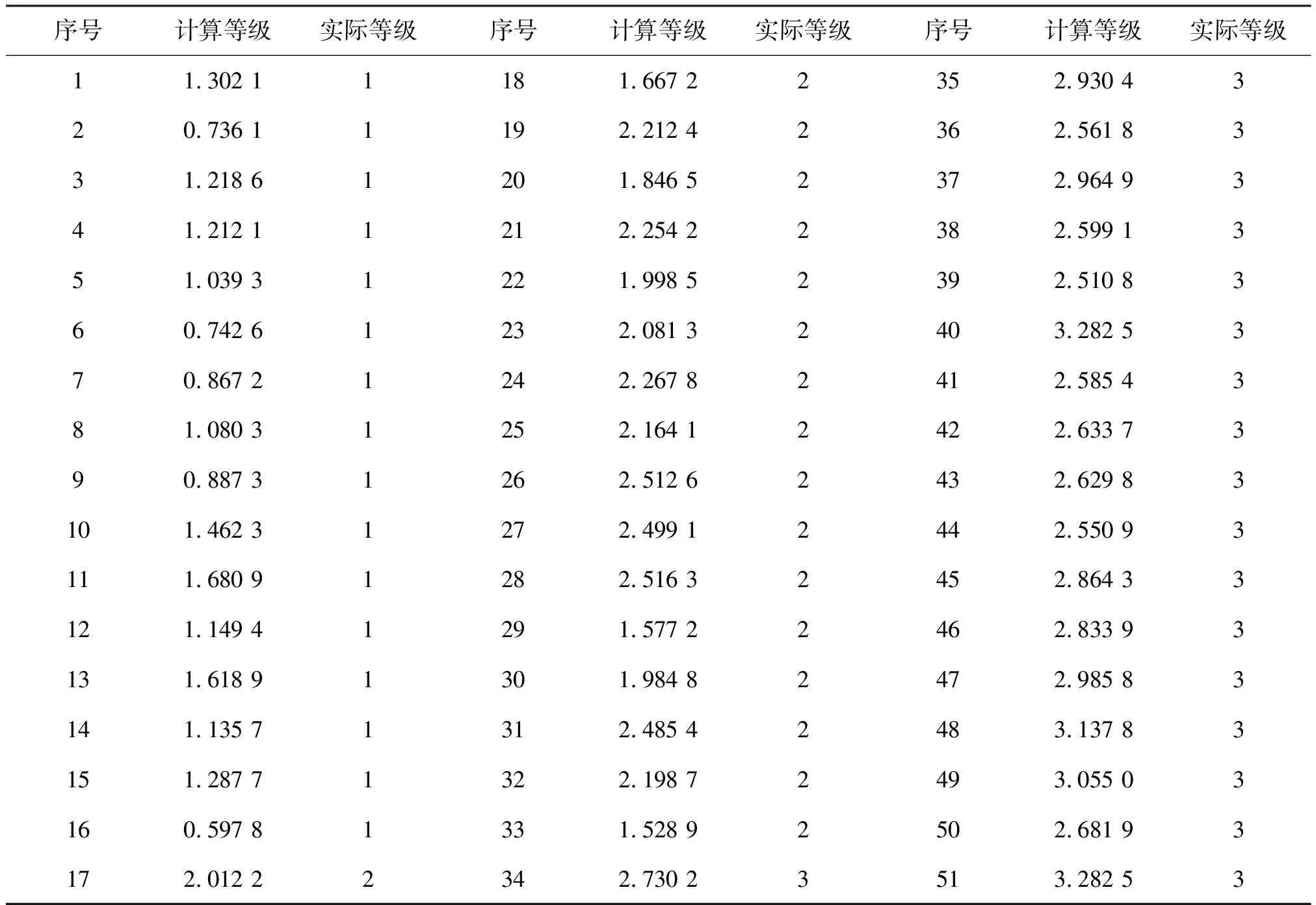
表3 猪肉等级判定结果Table 3 Results of pork grade
由表3可知,计算等级在[0.5 1.5)范围内划为1级,计算等级在[1.5 2.5)范围内划为2级,计算等级在[2.5 3.5)范围内划为3级。在51个样本中,序号11,13,26,28计算等级与实际等级不一致,此处判定的准确率为92.16%。
为了研究本文方法的鲁棒性,在实验中把所有样本(600张猪肉图像)平均分成10份,轮流将其中的9份作为训练数据,1份作为测试数据,作十折交叉验证,由此得到的10个准确率分别为:95.56%,91.86%,92.98%,93.47%,91.86%,95.43%,97.22%,94.48%,93.45%,95.69%,该方法的平均准确率达到94.25%,且每次的准确率都在90%以上。可以看出本文结合量子技术改进中值滤波和FCM在对猪肉颜色分级的问题上具有较强的鲁棒性(图13)。

图13 使用不同滤波方式的分级准确率Fig.13 Grading accuracy using different filtering methods
5 结论
本文利用量子理论的知识对传统中值滤波算法进行优化改进,实现了条件性中值滤波。仿真结果表明本文算法不仅有较强的去噪能力,还能根据条件滤波方式较好地保留图像细节[9],结合FCM和本文改进算法对猪肉颜色进行检测分级研究表明,两者结合的正确率要比单独使用FCM或FCM结合传统中值滤波高得多。本文的研究可为猪肉颜色分级的进一步研究提供参考。

